Przeczytaj

Znasz już wzory na objętość ostrosłupów prawidłowych:

objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy $a$ i wysokości $H$ wyraża się wzorem:
$V = \frac{\sqrt{3}}{12} a^{2} H$
objętość czworościanu foremnego o krawędzi $a$ to:
$V = \frac{a^{3} \sqrt{2}}{12}$
objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy $a$ i wysokości $H$ można obliczyć ze wzoru:
$V = \frac{a^{2} H}{3}$
objętość ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy $a$ i wysokości $H$ , to:
$V = \frac{\sqrt{3}}{2} a^{2} H$

Przykład 1

Objętość ostrosłupa prawidłowego trójkątnego wynosi $2 \sqrt{3}$ , a wysokość bryły jest równa $6$ . Obliczymy długość krawędzi podstawy tego ostrosłupa.

Rozwiązanie

Mamy $V = 2 \sqrt{3}$ .

Podstawiając do wzoru na objętość ostrosłupa prawidłowego trójkątnego otrzymujemy $\frac{\sqrt{3}}{12} a^{2} \cdot 6 = 2 \sqrt{3}$ .

Czyli $a^{2} = 4$ .

A zatem krawędź podstawy ma długość $2$ .

Przykład 2

Krawędź boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny podstawy pod kątem $45 °$ i ma długość $4$ . Obliczymy objętość tego ostrosłupa.

Rozwiązanie

Zróbmy rysunek pomocniczy.

R1NkkXhZ8BLkT

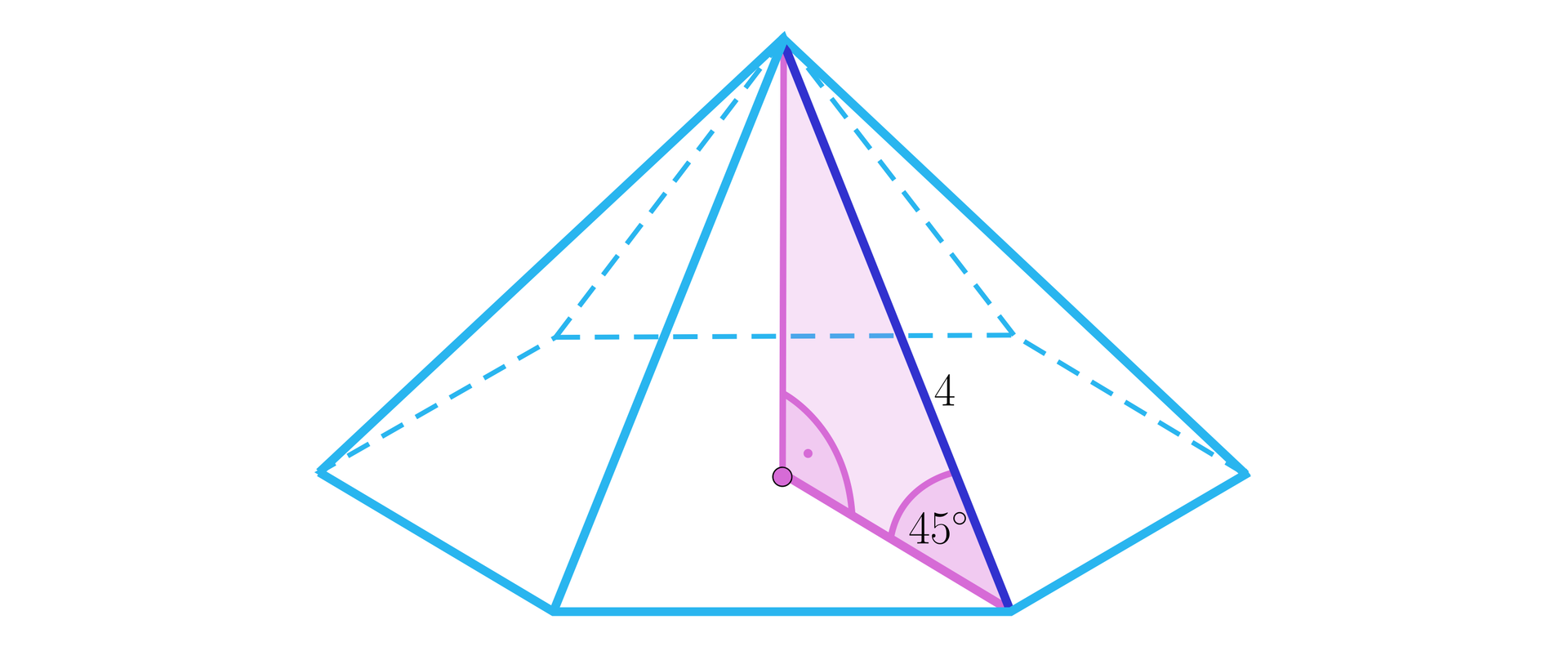
Ilustracja przedstawia ostrosłup prawidłowy sześciokątny. Zaznaczono jego wysokość oraz jedną z krawędzi ściany bocznej o długości 4, nachylony pod kątem 45 stopni do podstawy, a także połowę przekątnej podstawy domykającej trójkąt prostokątny zawarty między wysokością a wyróżnioną krawędzią.

Ze wzoru na przeciwprostokątną w trójkącie prostokątnym równoramiennym mamy, że wysokość ostrosłupa i długość połowy dłuższej przekątnej podstawy wynosi $2 \sqrt{2}$ .

Czyli $H = 2 \sqrt{2}$ i $a = 2 \sqrt{2}$ .

Podstawiamy do wzoru na objętość ostrosłupa prawidłowego sześciokątnego:

$V = \frac{\sqrt{3}}{2} \cdot {(2 \sqrt{2})}^{2} \cdot 2 \sqrt{2} = 8 \sqrt{6}$

Ważne!

Wzór ogólny na objętość ostrosłupa to:

V = \frac{1}{3} \cdot P_{p} \cdot H

gdzie:

$P_{p}$ – oznacza pole podstawy,

$H$ – wysokość.

Każdy z poprzednio podanych wzorów ma swoją genezę we wzorze ogólnym i powstaje przez zastąpienie pola podstawy wzorem na pole figury będącej podstawą danego ostrosłupa prawidłowego (w tych konkretnych przypadkach: trójkąta równobocznego, kwadratu i sześciokąta foremnego).

Jak poradzić sobie z obliczeniem pola podstawy ostrosłupa prawidłowego, który nie jest ostrosłupem prawidłowym trójkątnym, czworokątnym lub sześciokątnym?

Przykład 3

Wyprowadzimy wzór na pole podstawy oraz objętość ostrosłupa prawidłowego ośmiokątnego o krawędzi podstawy $a$ i wysokości ostrosłupa $H$ .

Rozwiązanie

Ośmiokąt foremny o boku $a$ można podzielić najdłuższymi przekątnymi na osiem przystających trójkątów równoramiennych o podstawie $a$ , ramionach $R$ (gdzie $R$ jest promieniem okręgu opisanego na ośmiokącie) i kącie między ramionami o mierze $360 ° : 8 = 45 °$ .

R2KOvuDgAk0mS

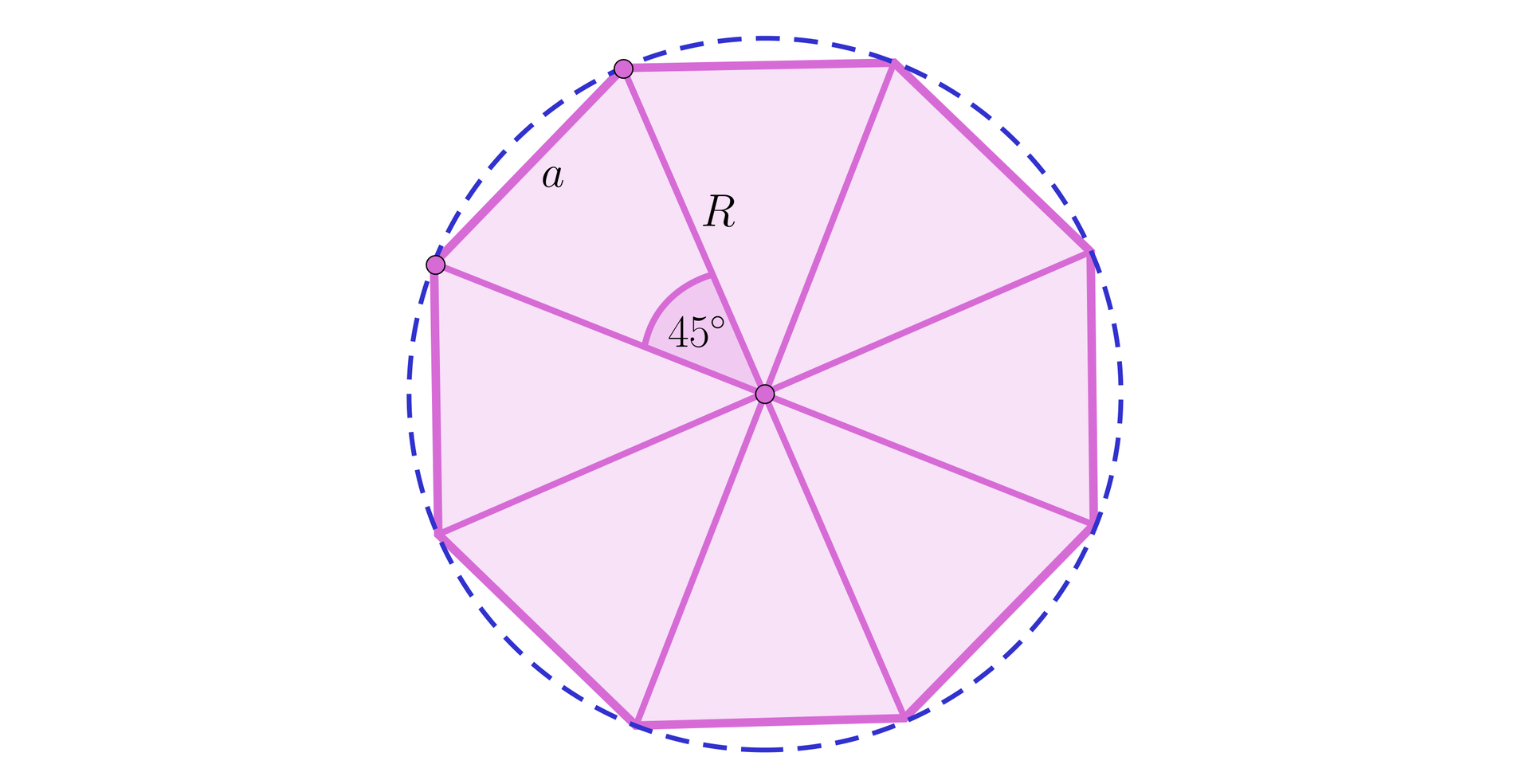
Ilustracja przedstawia ośmiokąt foremny wpisany w okrąg. Ośmiokąt został podzielony na osiem takich samych trójkątów. Środek ośmiokąta zaznaczono punktem. Odległość od środka ośmiokąta do wierzchołka ośmiokąta, będąca ramieniem trójkąta, jest równa R. Bok ośmiokąta, będący podstawą trójkąta ma długość a. Kąt w trójkącie, leżący przy środku ośmiokąta wynosi 45 stopni.

Obliczmy długość $R$ z twierdzenia cosinusów dla pojedynczego trójkąta:

a^{2} = R^{2} + R^{2} - 2 \cdot R \cdot R \cdot \cos 45 °

Mamy zatem $2 \cdot R^{2} - \sqrt{2} R^{2} = a^{2}$ .

Czyli $R^{2} = \frac{a^{2}}{2 - \sqrt{2}} = \frac{a^{2}}{2} (2 + \sqrt{2})$ .

Pole ośmiokąta to

$P = 8 \cdot P_{△} = 8 \cdot \frac{1}{2} \cdot R^{2} \cdot \sin 45 ° = 4 \cdot \frac{a^{2}}{2} (2 + \sqrt{2}) \cdot \frac{\sqrt{2}}{2} =$

$= a^{2} \sqrt{2} (2 + \sqrt{2}) = 2 a^{2} (\sqrt{2} + 1)$

A zatem $P_{p} = 2 a^{2} (\sqrt{2} + 1)$ .

Wzór na objętość ostrosłupa prawidłowego ośmiokątnego będzie więc mieć postać

$V = \frac{2 \cdot (\sqrt{2} + 1)}{3} \cdot a^{2} \cdot H$

Ważne!

Dla każdego wielokąta foremnego o danym boku możemy postępować w podobny sposób: wyznaczyć $R$ z twierdzenia cosinusów i obliczyć pole ze wzoru:

P = n \cdot \frac{1}{2} \cdot R^{2} \cdot \sin \frac{360 °}{n}

Przykład 4

Obliczymy objętość ostrosłupa prawidłowego $12$ –kątnego o krawędzi podstawy równej $4$ i wysokości $6$ .

Rozwiązanie

Obliczmy miarę kąta środkowego $360 ° : 12 = 30 °$ . Wyznaczamy długość $R$ z twierdzenia cosinusów:

$16 = 2 \cdot R^{2} - 2 \cdot R^{2} \cdot \cos 30 °$

Mamy $16 = (2 - \sqrt{3}) R^{2}$ , czyli $R^{2} = \frac{16}{2 - \sqrt{3}} = 16 (2 + \sqrt{3})$ .

Podstawiając do wzoru na pole wielokąta foremnego mamy

$P_{p} = 12 \cdot \frac{1}{2} \cdot 16 (2 + \sqrt{3}) \cdot \sin 30 ° = 48 (2 + \sqrt{3})$ .

Zatem objętość wynosi $V = \frac{1}{3} \cdot 48 (2 + \sqrt{3}) \cdot 6 = 96 (2 + \sqrt{3})$ .

Uwaga!

Powyższe rozumowanie sprawdza się dla każdego ostrosłupa, którego podstawą jest wielokąt foremny – nie musi to być ostrosłup prawidłowyostrosłup prawidłowyostrosłup prawidłowy.

Przykład 5

Podstawą ostrosłupa na rysunku jest wielokąt foremny, a wysokością odcinek zaznaczony na granatowo.

R19grmed0RlFq

Ilustracja przedstawia ostrosłup pochyły o podstawie ośmiokąta. Krawędź ośmiokąta ma długość trzy. Wysokość, tego ostrosłupa, której spodek leży poza płaszczyzną podstawy ma długość sześć.

Obliczymy objętość tego ostrosłupa.

Rozwiązanie

Liczymy objętość ze wzoru

$V = \frac{1}{3} \cdot P_{p} \cdot H$ ,

gdzie:
$P_{p} = 2 a^{2} (\sqrt{2} + 1)$ , ponieważ w podstawie jest ośmiokąt foremny.

Mamy wtedy $V = \frac{1}{3} \cdot 18 (\sqrt{2} + 1) \cdot 6 = 36 (\sqrt{2} + 1)$ .

Przykład 6

Dany jest ostrosłup o podstawie kwadratu, jak na rysunku.

RoIuanF6bq75i

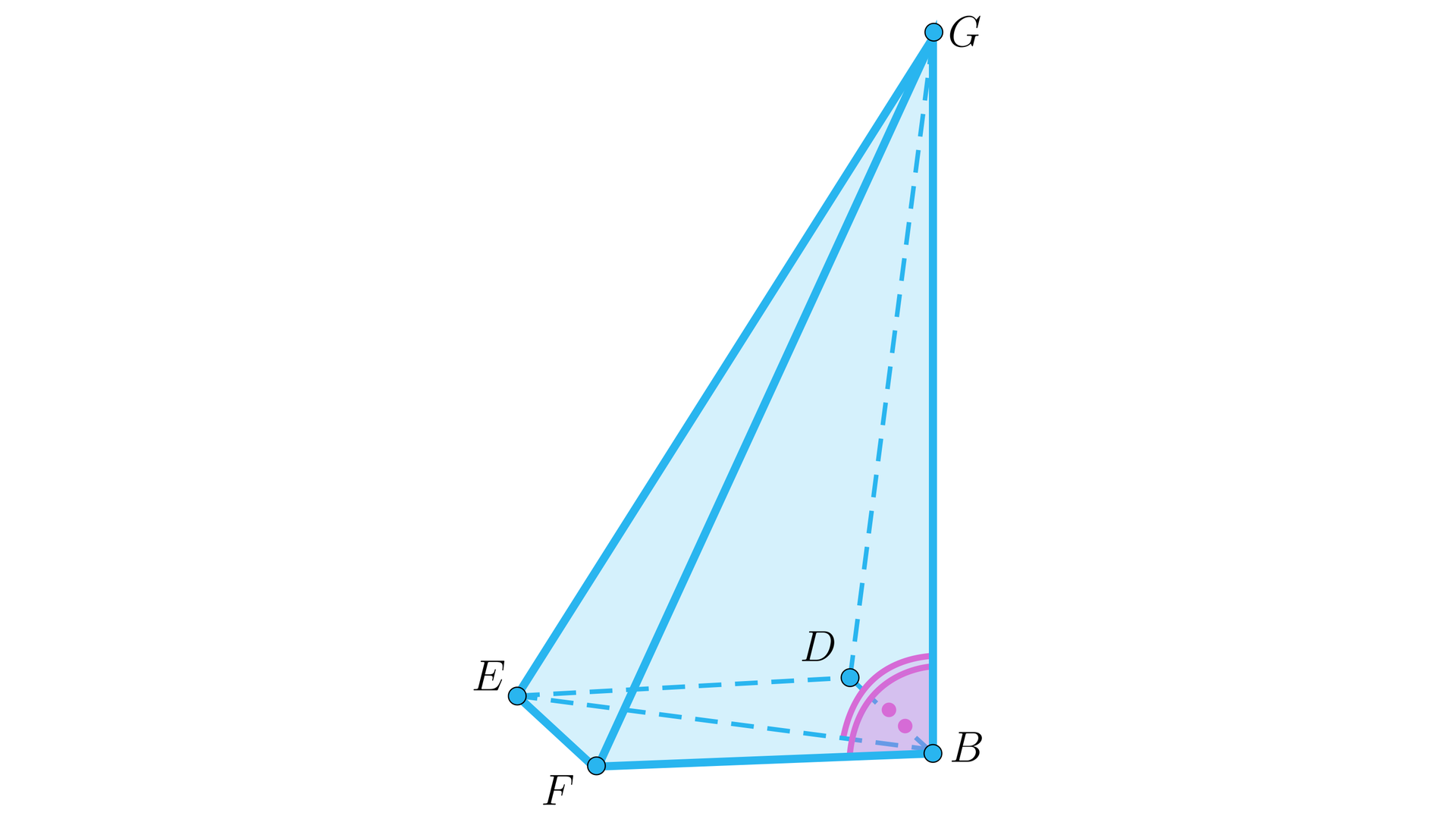
Ilustracja przedstawia ostrosłup, którego podstawą jest kwadrat B D E F. W podstawie zaznaczono przekątną BE. Wierzchołek górny podpisano literą G, krawędź boczna BG jest pod kątem prostym do krawędzi podstawy oraz do przekątnej podstawy.

Krawędź $F B$ ma długość $6$ , krawędź $B G$ jest prostopadła do płaszczyzny podstawy i ma długość $8$ . Obliczymy objętość tego ostrosłupa.

Rozwiązanie

Krawędź $B G$ jest wysokością tego ostrosłupa.

Obliczamy objętość ze wzoru $V = \frac{1}{3} \cdot P_{p} \cdot H$ .

Mamy zatem $V = \frac{1}{3} \cdot 6^{2} \cdot 8 = 96$ .

Wiecie już, że podstawa ostrosłupa może być dowolnym wielokątem. Obliczaliście już objętość ostrosłupów trójkątnych i czworokątnych. Jesteśmy w stanie policzyć objętość ostrosłupa, pod warunkiem, że możemy wyznaczyć jego pole podstawy i wysokość.

Przykład 7

Obliczymy objętość ostrosłupa, w którego podstawie znajduje się romb o boku długości $5$ i krótszej przekątnej $6$ , jeżeli wiemy, że spodkiem wysokości ostrosłupaspodek wysokości ostrosłupaspodkiem wysokości ostrosłupa jest środek ciężkości podstawyśrodek ciężkości rombuśrodek ciężkości podstawy, a dłuższa krawędź boczna ma długość $4 \sqrt{5}$ .

Rozwiązanie

Obliczamy długość drugiej przekątnej rombu z twierdzenia Pitagorasa:

$x^{2} + 3^{2} = 5^{2}$ , stąd oczywiście $x = 4$ .

Cała przekątna ma więc długość $8$ .

Dłuższa krawędź boczna, połowa dłuższej przekątnej podstawy i wysokość ostrosłupa są bokami tego samego trójkąta prostokątnego. Obliczymy wysokość ostrosłupa z twierdzenia Pitagorasa.

R2CxwYyEXHy6S

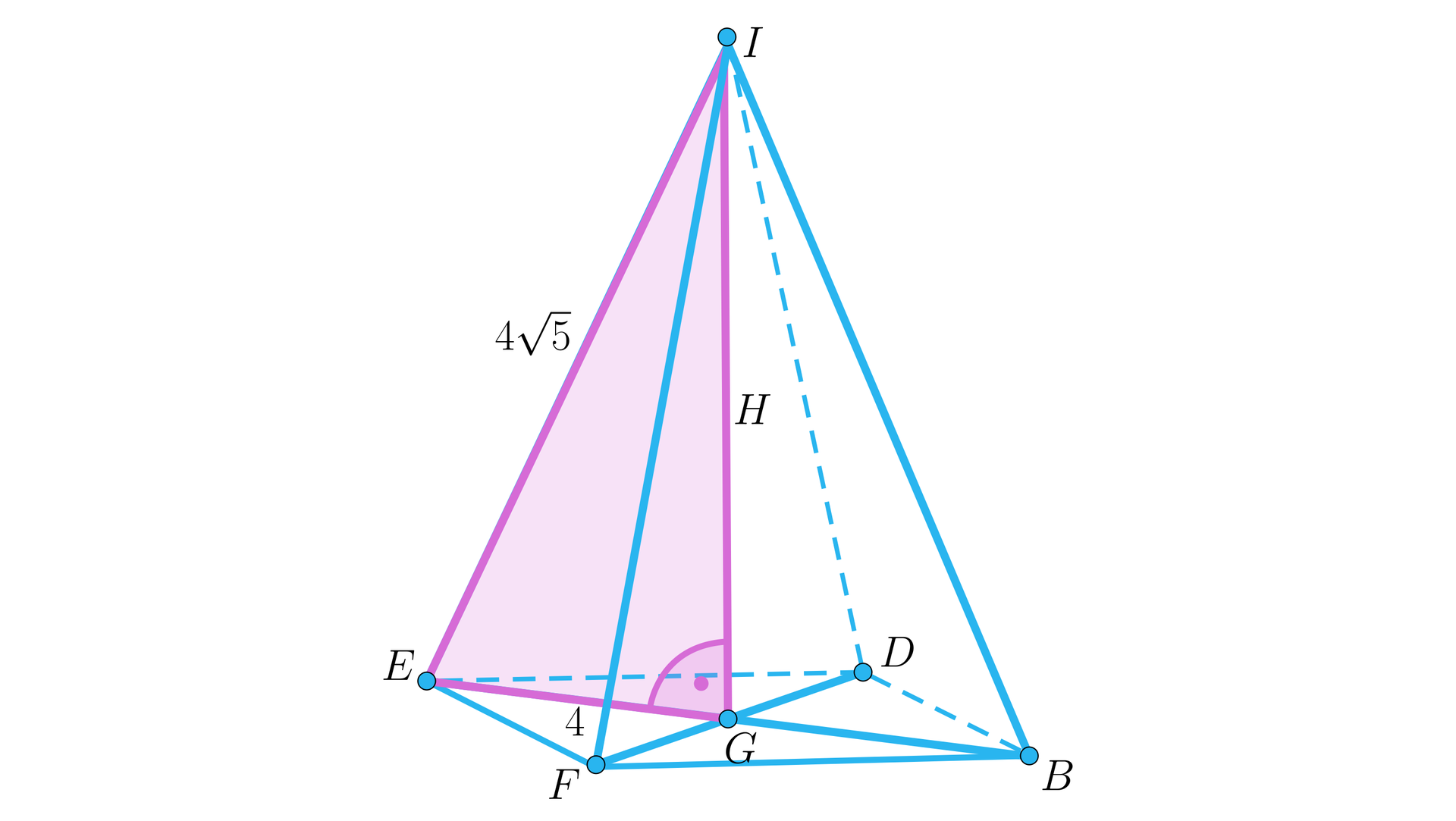
Ilustracja przedstawia ostrosłup, którego podstawą jest romb B D E F. W podstawie zaznaczono jej przekątne. Wierzchołek górny podpisano literą I, W ostrosłupie zaznaczono wysokość, spodek wysokości leży na przecięciu się przekątnych podstawy i jest podpisany literą G. W ostrosłupie zaznaczono trójkąt prostokątny E G I. Przeciwprostokątna EI ma długość 45, a przyprostokątna EG ma długość cztery.

Mamy zatem $4^{2} + H^{2} = {(4 \sqrt{5})}^{2}$ , a stąd $H = 8$ .

Obliczamy objętość ostrosłupa

$V = \frac{1}{3} \cdot P_{p} \cdot H = \frac{1}{3} \cdot \frac{e \cdot f}{2} \cdot H = \frac{1}{3} \cdot \frac{6 \cdot 8}{2} \cdot 8 = 64$ .

Przykład 8

Obliczymy objętość ostrosłupa o wysokości $H = 6$ , jeżeli jego podstawą jest wielokąt jak na rysunku (przyjmujemy, że jedna kratka to jedna jednostka).

Rv9HP3I9zooQZ

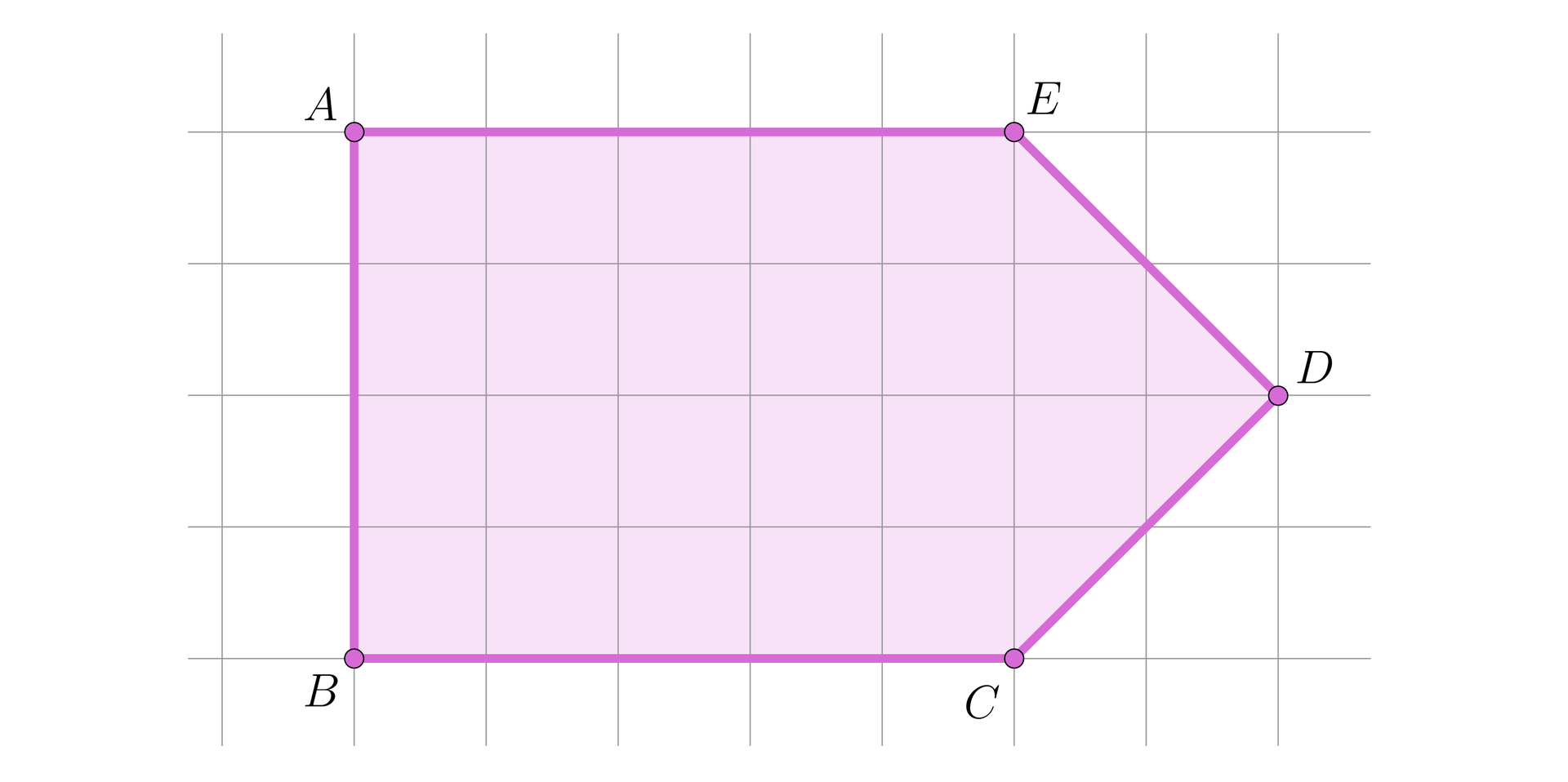
Ilustracja przedstawia kartkę w kratkę, na której narysowano pięciokąt o wierzchołkach A B C D, przy czym krawędź AB jest pionowa i ma długość czterech kratek, krawędź AE jest pozioma, biegnie w prawą stronę i ma długość pięciu kratek. Krawędź BC jest równoległa do krawędzi AE i również ma długość pięciu kratek. Odcinek ED biegnie ukośnie, po przekątnej kratek przesuwając się od punktu e dwie kratki w dół i dwie kratki w prawo, natomiast krawędź CD biegnie ukośnie po przekątnych kratek przesuwając się o dwie kratki do góry i dwie kratki w prawo.

Rozwiązanie

Pięciokąt na rysunku można podzielić na dwa trapezy prostokątne o podstawach $5$ i $7$ oraz wysokości $2$ .

A zatem $P_{p} = \frac{(5 + 7) \cdot 2}{2} \cdot 2 = 24$ .

Stąd objętość $V = \frac{1}{3} \cdot 24 \cdot 6 = 48$ .

Słownik

ostrosłup prawidłowy

ostrosłup, którego podstawą jest wielokąt foremny, a ściany boczne są przystającymi trójkątami równoramiennymi

spodek wysokości ostrosłupa

rzut prostopadły wierzchołka ostrosłupa na płaszczyznę podstawy

środek ciężkości rombu

punkt przecięcia przekątnych rombu

Wprowadzenie

Animacja 3D

Jak poradzić sobie z obliczeniem pola podstawy ostrosłupa prawidłowego, który nie jest ostrosłupem prawidłowym trójkątnym, czworokątnym lub sześciokątnym?

Słownik