Przeczytaj
W tym materiale zajmiemy się analizą własności ostrosłupów w zależności od ich liczby ścian, krawędzi i wierzchołków. Zauważmy, że wprost z definicji ostrosłupa wynika, że jeżeli podstawą ostrosłupa jest dany -kąt, wówczas prawdziwe są następujące obserwacje.
Ostrosłup ten posiada dokładnie wierzchołków.
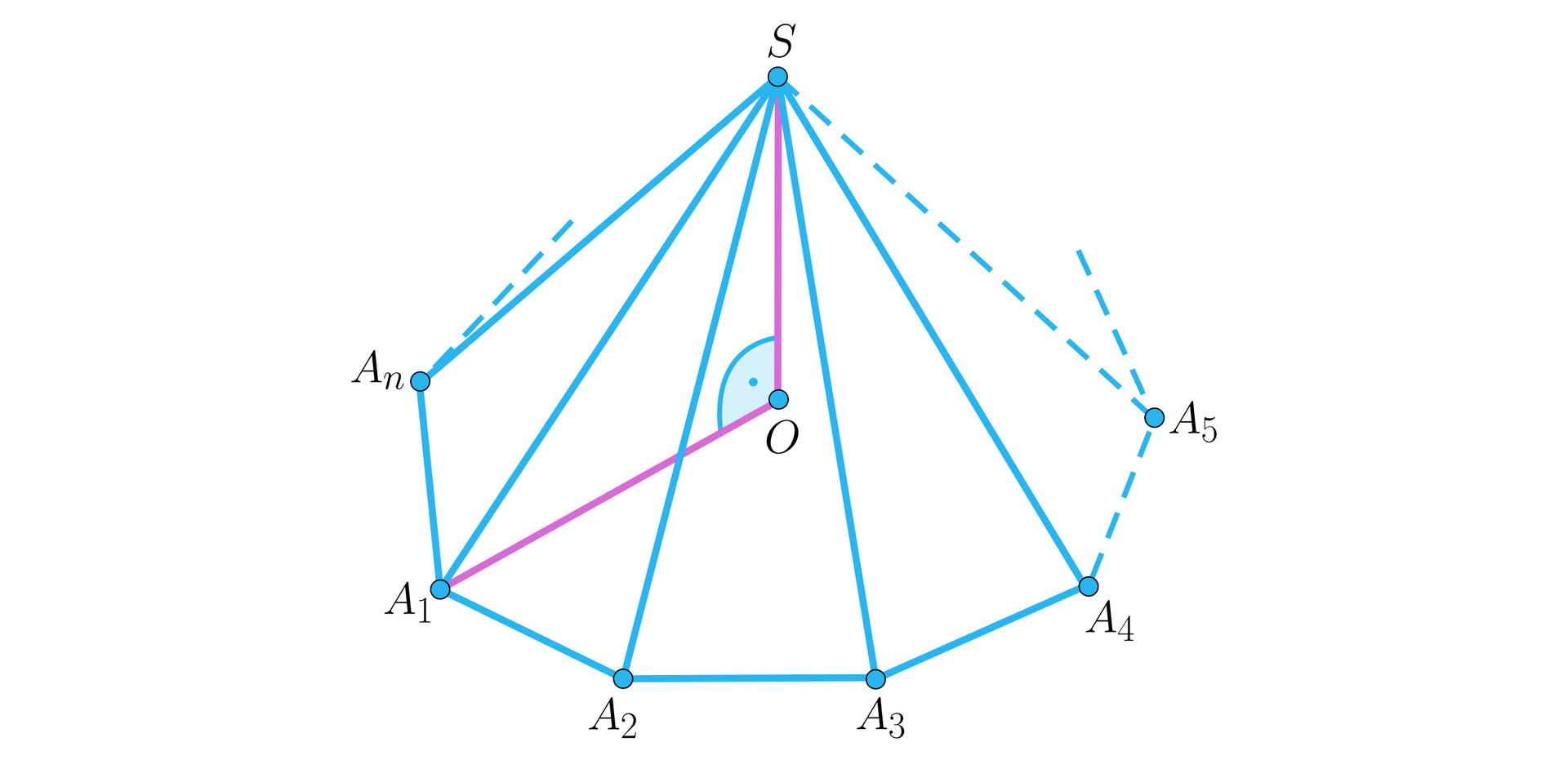
Istotnie, wierzchołków ostrosłupa należy do płaszczyzny podstawy, zaś jeden jest wspólnym wierzchołkiem ścian bocznych.
Ostrosłup ten posiada dokładnie krawędzi.

Faktycznie, krawędzi ostrosłupa to boki wielokąta podstawy. Z każdego wierzchołka podstawy (których to wierzchołków jest oczywiście ) poprowadzona jest dokładnie jedna krawędź boczna, łącząca ten wierzchołek podstawy z (pojedynczym) wierzchołkiem całego ostrosłupa. W sumie daje to krawędzi ostrosłupa.
Ostrosłup ten posiada dokładnie ścian.
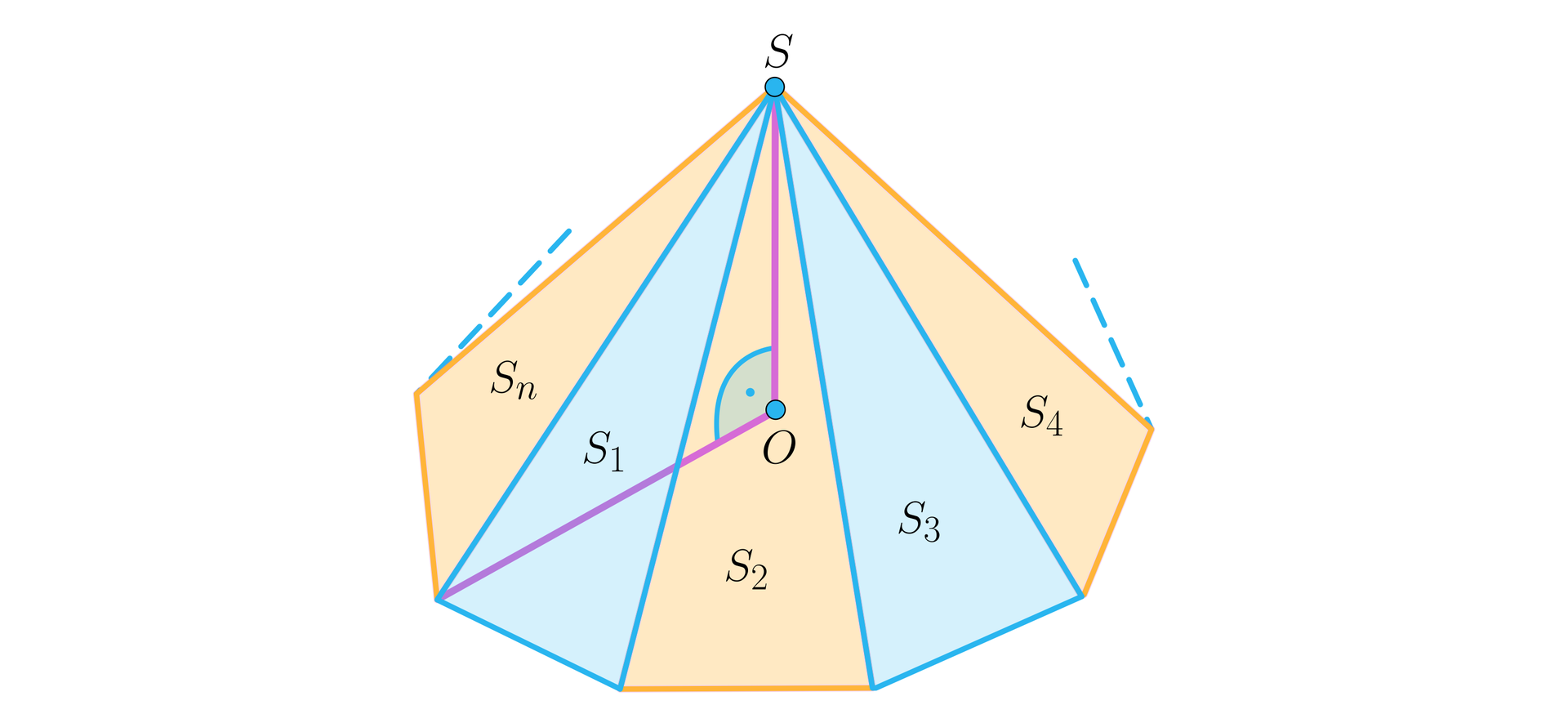
Aby to pokazać, zauważmy, że ścian to trójkąty tworzące ściany boczne. Ich podstawami są boki -kąta podstawy, która jest ostatnią -szą ścianą naszej bryły.
W wieku Leonard Euler odkrył prostą zależność między liczbą wierzchołków, ścian i krawędzi dowolnego wielościanuwielościanu wypukłego. Zależność tą nazywamy dziś twierdzeniem Eulera dla wielościanów, albo też wzorem Eulera. Legenda mówi, że Euler odkrył tę zależność przez przypadek, próbując klasyfikować wielościany ze względu na liczbę ich ścian, analogicznie do znanej mu klasyfikacji wielokątów w zależności od liczby boków. Euler szybko zauważył jednak, że wielościany o równej liczbie ścian mogą mieć jednak różne liczby wierzchołków i krawędzi. Ostatecznie zaczął rozpatrywać jednocześnie wszystkie trzy wielkości i sformułował następujący związek.
Liczba krawędzi wielościanu wypukłego jest o dwa mniejsza od sumy liczby wierzchołków i liczby ścian tego wielościanu.
Inaczej twierdzenie można to sformułować następująco
Niech oznacza liczbę wierzchołków, liczbę krawędzi, zaś liczbę ścian wielościanu. Dla każdego wielościanu wypukłego zachodzi równość
Rozważmy przykład ilustrujący wzór Eulera dla ostrosłupa o podstawie czworokąta.

Możemy łatwo policzyć korzystając z rysunku albo modelu takiego ostrosłupa liczbę jego wierzchołków, krawędzi i ścian. W poniższej tabeli zebraliśmy wartości poszczególnych składowych ze wzoru Eulera.
Nazwa wielościanu | Ostrosłup czworokątny |
|---|---|
Liczba wierzchołków | |
Liczba ścian | |
Liczba krawędzi |
Zgodnie ze wzorem Eulera zachodzi równość .
Zajmiemy się teraz twierdzeniem Eulera w przypadku dowolnego ostrosłupa o podstawie -kątnej.

Przyjmijmy oznaczenie na liczbę wierzchołków wielokąta będącego podstawą ostrosłupa. Z wcześniejszych obserwacji wiemy, że zachodzą związki
, oraz .
Stąd otrzymujemy równość .
Zauważmy, że w powyższym dowodzie w żaden sposób nie wykorzystaliśmy informacji, że ostrosłup jest wypukły. Związki określające ilość krawędzi, wierzchołków i ścian ostrosłupa w zależności od ilości boków wielokąta podstawy są prawdziwe zawsze, nawet, gdy ostrosłup ten nie jest bryłą wypukłąbryłą wypukłą. Możemy zatem stwierdzić, że wzór Eulera jest prawdziwy dla każdego ostrosłupa (nie tylko wypukłego).
Dzięki opisanym własnościom, można rozwiązywać zadania, w których musimy dokonać analizy bryły na podstawie wiadomości o liczbie jej ścian, krawędzi oraz wierzchołków.
Ile ścian bocznych ma ostrosłup o krawędziach?
Rozwiązanie
Jeżeli jest to ostrosłup -kątny, to liczba jego krawędzi jest równa . Stąd , co oznacza, że ostrosłup ten ma dokładnie ścian.
Liczba krawędzi pewnego ostrosłupa jest o większa od liczby jego wszystkich wierzchołków. Oblicz, ile ścian ma ten ostrosłup.
Rozwiązanie
Pamiętając, że dla ostrosłupa o podstawie -kątnej liczba krawędzi wynosi zaś liczba wierzchołków , otrzymujemy następującą zależność:
.
Stąd już bezpośrednio wynika, że . Oznacza to, że omawianym ostrosłupem jest ostrosłup o podstawie osiemnastokątnej, a jego ilość ścian jest równa .
Charakterystyką Eulera wielościanu nazywamy liczbę , gdzie oznacza liczbę ścian wielościanu, liczbę jego wierzchołków, a liczbę jego krawędzi. Rozpatrzmy ostrosłup prawidłowy czworokątny, w którym krawędź podstawy jest równa wysokości ściany bocznej.
Podajemy charakterystykę Eulera omawianego ostrosłupa.
Zauważmy, że charakterystyka Eulera jest sumą, która występuje w twierdzeniu Eulera o wielościanach wypukłych. Dla ostrosłupa (jak i dla każdego wielościanu wypukłego) mamy zatem .Do ściany danego ostrosłupa doklejamy identyczny ostrosłup. Podajemy charakterystykę Eulera wielościanu, który powstał po sklejeniu dwóch ostrosłupów.
R3MIhB6YqIb0r 
Jeżeli skleimy dwa ostrosłupy, to ilość ścian otrzymanej bryły będzie równa sumie ilości ścian danych ostrosłupów pomniejszonej o (bo dwie ściany zniknęły we wnętrzu bryły). Ilość krawędzi otrzymanej bryły będzie równa sumie ilości krawędzi każdego z ostrosłupów pomniejszonej o (bo trzy krawędzi pokryły się). Ilość wierzchołków otrzymanej bryły będzie równa sumie ilości wierzchołków danych ostrosłupów pomniejszonej o (bo trzy wierzchołki zostały zlepione). Ostatecznie .
Charakterystyka Eulera otrzymanego wielościanu jest zatem równa charakterystyce Eulera wyjściowego ostrosłupa.Postępując analogicznie, do ściany doklejamy kolejny ostrosłup. Określ, ile maksymalnie identycznych ostrosłupów opisanych w zadaniu można skleić w ten sposób ze sobą.
Rozpatrzmy w danym ostrosłupie trójkąt, którego wierzchołkami są środki dwóch przeciwległych krawędzi podstawy i wierzchołek górny ostrosłupa.RGZhiKXdwxV23 
Ponieważ zgodnie z warunkami zadania wysokość ściany bocznej jest równa krawędzi podstawy, to ten trójkąt jest trójkątem równobocznym. Gdy doklejamy kolejne ostrosłupy, trójkąty te sklejają się bokami należącymi do sklejanej ściany i są współpłaszczyznowe. Ponieważ kąt wewnętrzny trójkąta równobocznego jest równy , to zlepimy maksymalnie sześć ostrosłupów, otrzymując w omawianym przekroju kąt pełny .
Podajemy charakterystykę Eulera wielościanu sklejonego z tej maksymalnej liczby ostrosłupów.
Oto szkic otrzymanego wielościanu.RpkzudWEWvmbQ 
Na zamieszczonym rysunku możemy zauważyć, że omawiany wielościan sklejony z sześciu ostrosłupów ma: ścian, wierzchołków oraz krawędzi. Obliczając jego charakterystykę Eulera otrzymujemy . Oznacza to, że po sklejeniu ostatnich ścian i domknięciu „pierścienia” otrzymamy wielościan, którego charakterystyka jest różna od charakterystyki użytych ostrosłupów.
Słownik
część przestrzeni (bryła) ograniczona ze wszystkich stron wielokątami leżącymi w różnych płaszczyznach wraz z tymi wielokątami
zbiór punktów, który spełnia warunek, że każde dwa punkty należące do tego zbioru można połączyć odcinkiem zawartym w tym zbiorze