Przeczytaj
Funkcje liczboweFunkcje liczbowe można opisywać wzorem zapisanym za pomocą kilku wyrażeń w różnych przedziałach. W jaki sposób należy rysować wtedy wykres tak opisanej funkcji? Odpowiedź na to pytanie uzyskamy po przeanalizowaniu poniższych przykładów.
Naszkicujmy wykres funkcji określonej w zbiorze liczb rzeczywistych.
Funkcja ta ma swoją nazwę. Jest to funkcja signum, sgn (łac. signum „znak”).

Naszkicujemy wykres funkcji .
Odczytamy z rysunku współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.
Rozwiązanie:
Funkcja opisana jest za pomocą wzoru wyrażonego trzema wyrażeniami. W celu narysowania wykresu wykonamy odpowiednie tabelki częściowe.
Pierwszą tabelkę częściową wykonamy dla funkcji opisanej pierwszym wyrażeniem i dla kilku argumentów należących do pierwszego przedziału.
Argumenty i wartości funkcji | ||||
|---|---|---|---|---|
Druga część wykresu nie wymaga tabelki. Dla każdego argumentu , takiego, że funkcja ma stałą wartość równą trzy.
Dla argumentów należących do trzeciego przedziału wykonamy tabelkę częściową.
Argumenty i wartości funkcji | ||||
|---|---|---|---|---|
Na podstawie wyznaczonych współrzędnych, szkicujemy wykres funkcji.
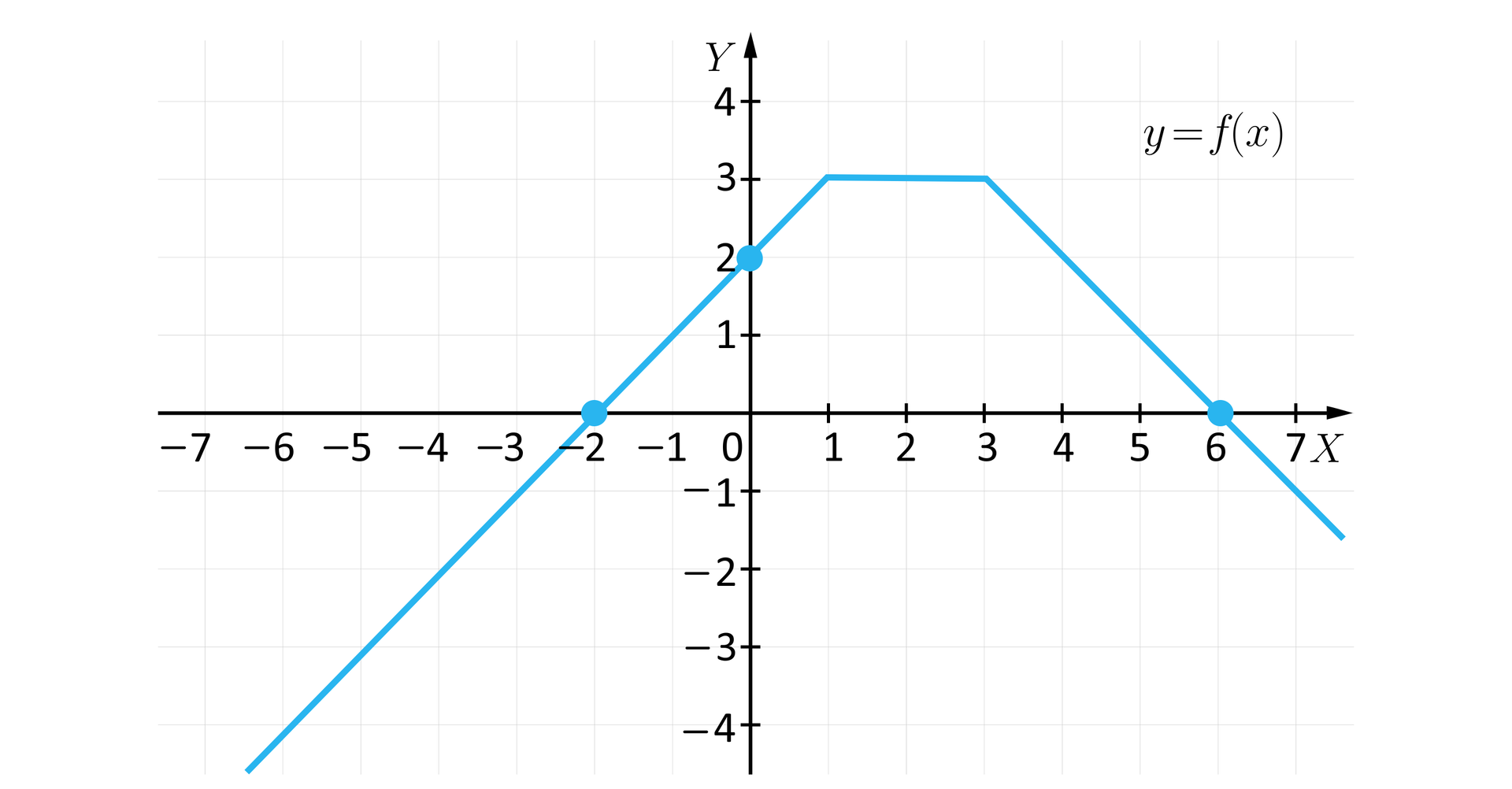
Korzystając z wykresu odczytujemy współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.
Wykres funkcji ma dwa punkty wspólne z osią – są to punkty o współrzędnych i .
Z osią wykres funkcji ma jeden punkt wspólny o współrzędnych .
Naszkicujemy wykres funkcji .
Odczytamy z wykresu współrzędne punktów przecięcia wykresu funkcji z osiami układu współrzędnych.
Czy wykres funkcji jest linią ciągłą?
Rozwiązanie:
Funkcja opisana jest wzorem zapisanym za pomocą trzech wyrażeń. W celu narysowania wykresu funkcji wykonamy dwie tabelki częściowe.
Pierwszą tabelkę wykonamy dla funkcji opisanej pierwszym wzorem i argumentów należących do pierwszego przedziału.
Argumenty i wartości funkcji | |||
|---|---|---|---|
Funkcja opisana drugim wzorem jest określona dla trzech argumentów.
Argumenty i wartości funkcji | |||
|---|---|---|---|
Dla argumentów należących do przedziału trzeciego wykonujemy tabelkę częściową.
Argumenty i wartości funkcji | ||||
|---|---|---|---|---|
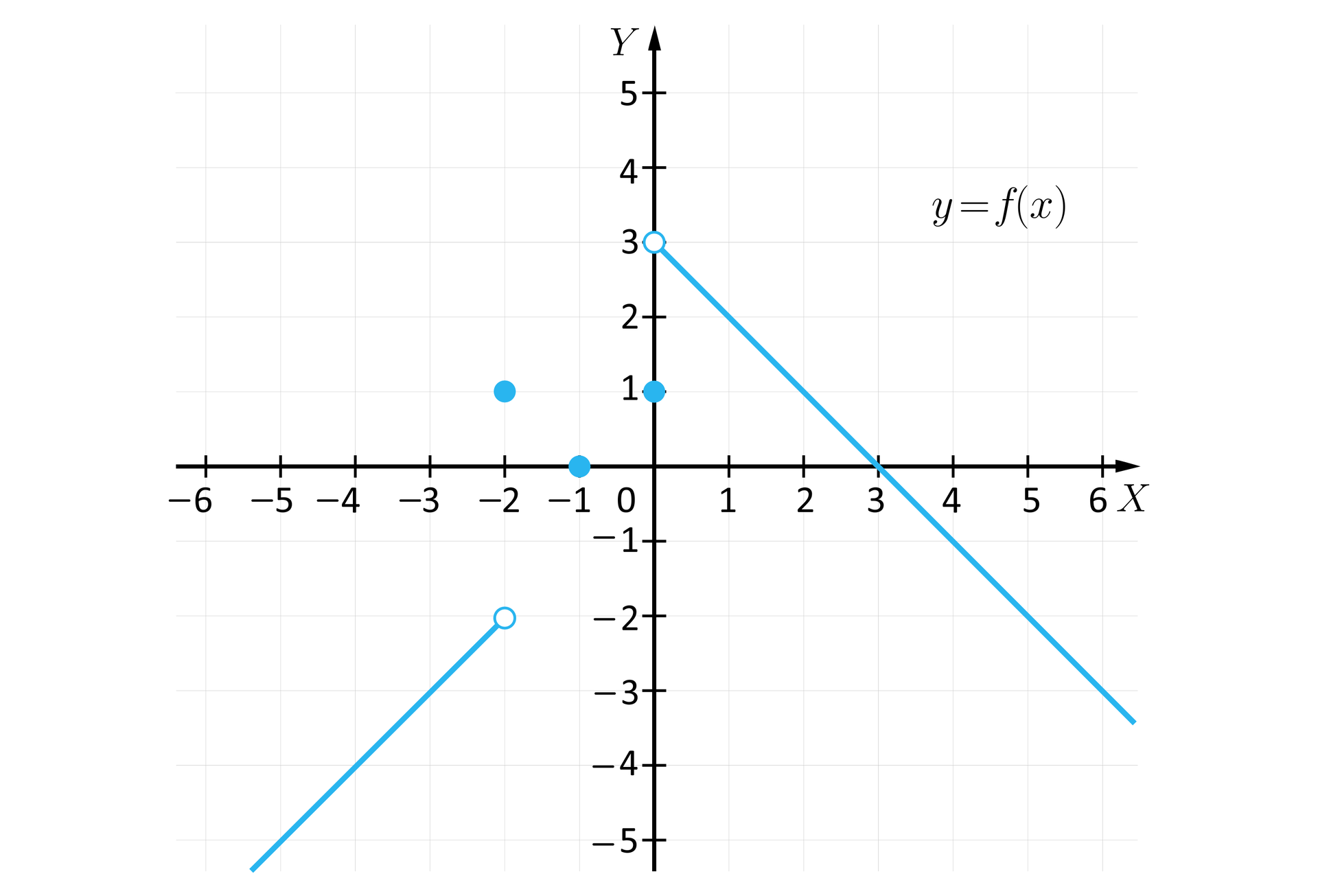
Wykres funkcji ma jeden punkt wspólny z osią . Jest to punkt o współrzędnych .
Z osią wykres ma dwa punkty wspólne. Są nimi punkty o współrzędnych: i .
Wykres funkcji nie jest linią ciągłą.
W matematyce niekiedy posługujemy się funkcjami zmiennej , których wzór składa się z kilku wyrażeń połączonych klamrą. Aby naszkicować wykres tak opisanej funkcji należy naszkicować wykres funkcji dla każdej części wzoru, uwzględniając przedział liczbowy, do którego dana część wzoru jest przypisana. Wykresy szkicujemy w tym samym układzie współrzędnych.
Słownik
funkcja, której dziedzina i zbiór wartości to zbiory liczbowe