Przeczytaj

okrąg wpisany w trójkąt

Definicja: okrąg wpisany w trójkąt

Okrąg wpisany w trójkąt to okrąg, który jest styczny do wszystkich boków trójkąta.

Rf7VWjMqtFYm4

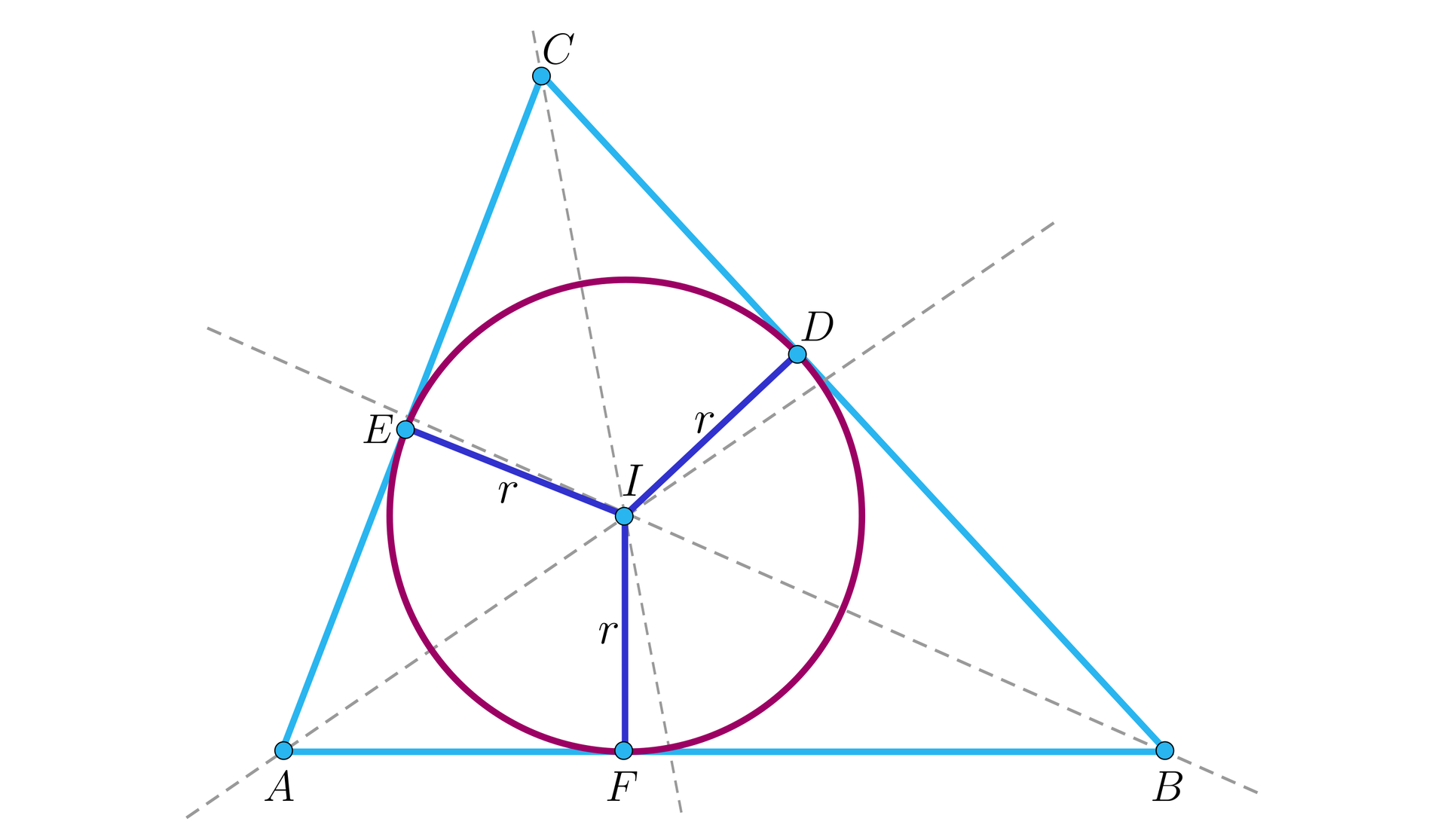
Ilustracja przedstawia trójkąt A B C, w który wpisano okrąg, środek okręgu I leży na przecięciu przerywanych prostych, w których zawierają się wysokości trójkątów. Punkty styczne trójkąta i okręgu są następujące: na boku BC leży punkt D, na boku AC leży punkt E, na boku AB leży punkt F. Odcinki: DI, EI i FI są podpisane literą r.

Odcinki łączące środek okręgu wpisanego z punktami styczności znajdującymi się na bokach trójkąta są do tych boków prostopadłe i są promieniami tego okręgu.

Czasem używa się także pojęcia koła wpisanego w trójkąt – jest to koło, zawarte w trójkącie i którego brzeg jest styczny do wszystkich boków wielokąta.

W każdy trójkąt można wpisać okrąg

Pokażemy, że dwusieczne kątów wewnętrznych dowolnego trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w ten trójkąt:

RRxjQhEcJyF14

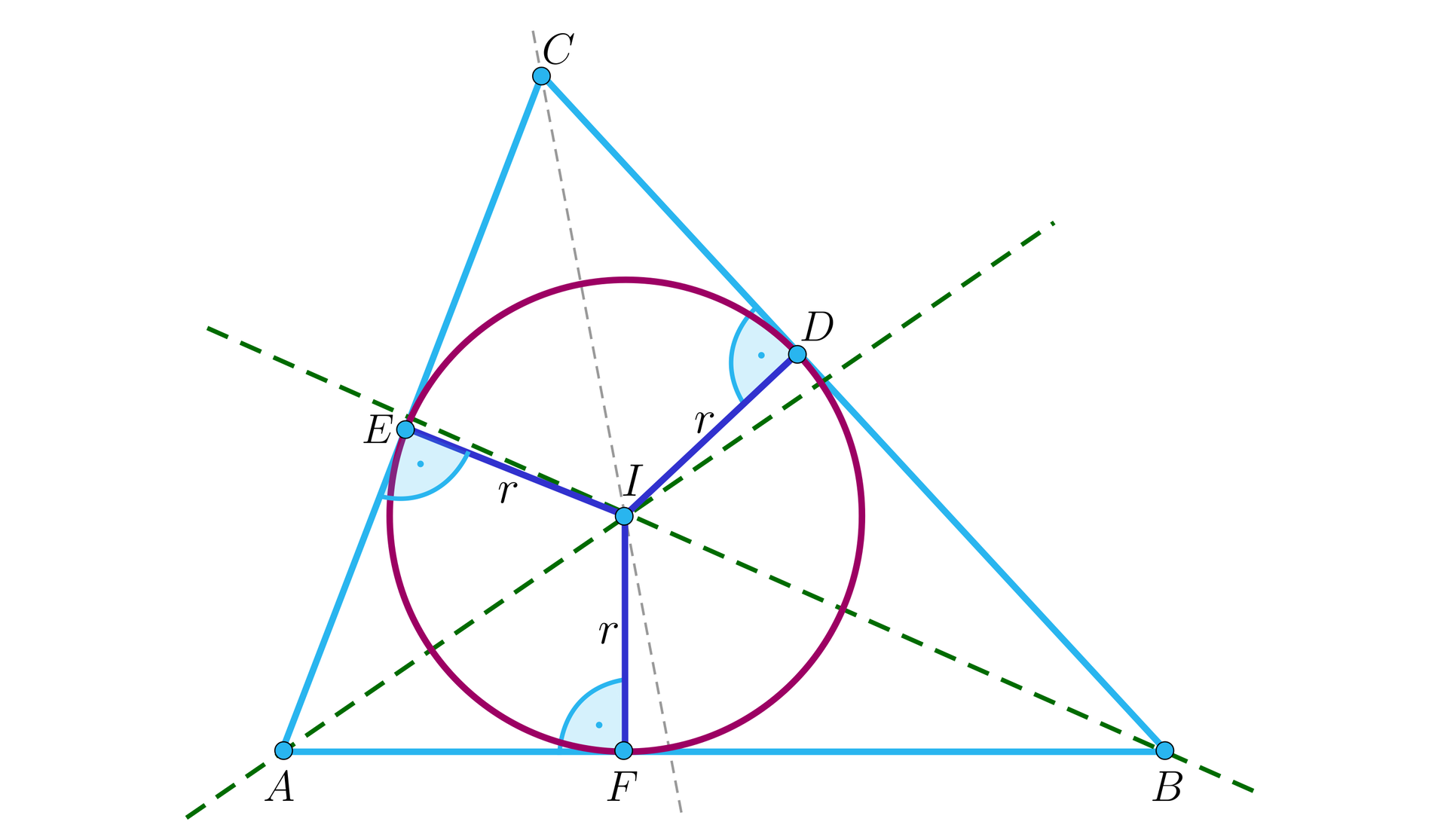
Przypomnijmy, że dwusieczna kątadwusieczna kątadwusieczna kąta jest zawarta w osi symetrii kąta, a więc jest zbiorem punktów równoodległych od ramion tego kąta.

Rozważmy punkt przecięcia dwusiecznych kątów $B A C$ i $A B C$ - nazwijmy go $I$ .
Ponieważ punkt $I$ leży na dwusiecznej kąta w trójkąciedwusieczna kąta w trójkąciedwusiecznej kąta w trójkącie $B A C$ , to jest on równoodległy od boków $A B$ i $A C$ , czyli $|I F| = |I E|$ . Podobnie, ponieważ leży też na dwusiecznej kąta $A B C$ to jest on równoodległy od boków $A B$ i $B C$ (czyli $|I F| = |I D|$ ). Z równości $|I F| = |I E|$ oraz $|I F| = |I D|$ wynika, że $|I E| = |I D|$ , czyli, ze punkt $I$ jest równoodległy od ramion $C A$ i $C B$ , więc leży na dwusiecznej kąta $A C B$ .

Zatem dwusieczne kątów przecinają się w punkcie $I$ . Odcinki $I D$ , $I E$ , $I F$ są równej długości, nazwijmy ją $r$ . Odcinki te są również prostopadłe do boków, więc okrąg o środku w punkcie $I$ i promieniu $r$ jest styczny do każdego z boków trójkąta.

Pole trójkąta opisanego na okręgu o promieniu $r$

R7EBmpnZ2q3BE

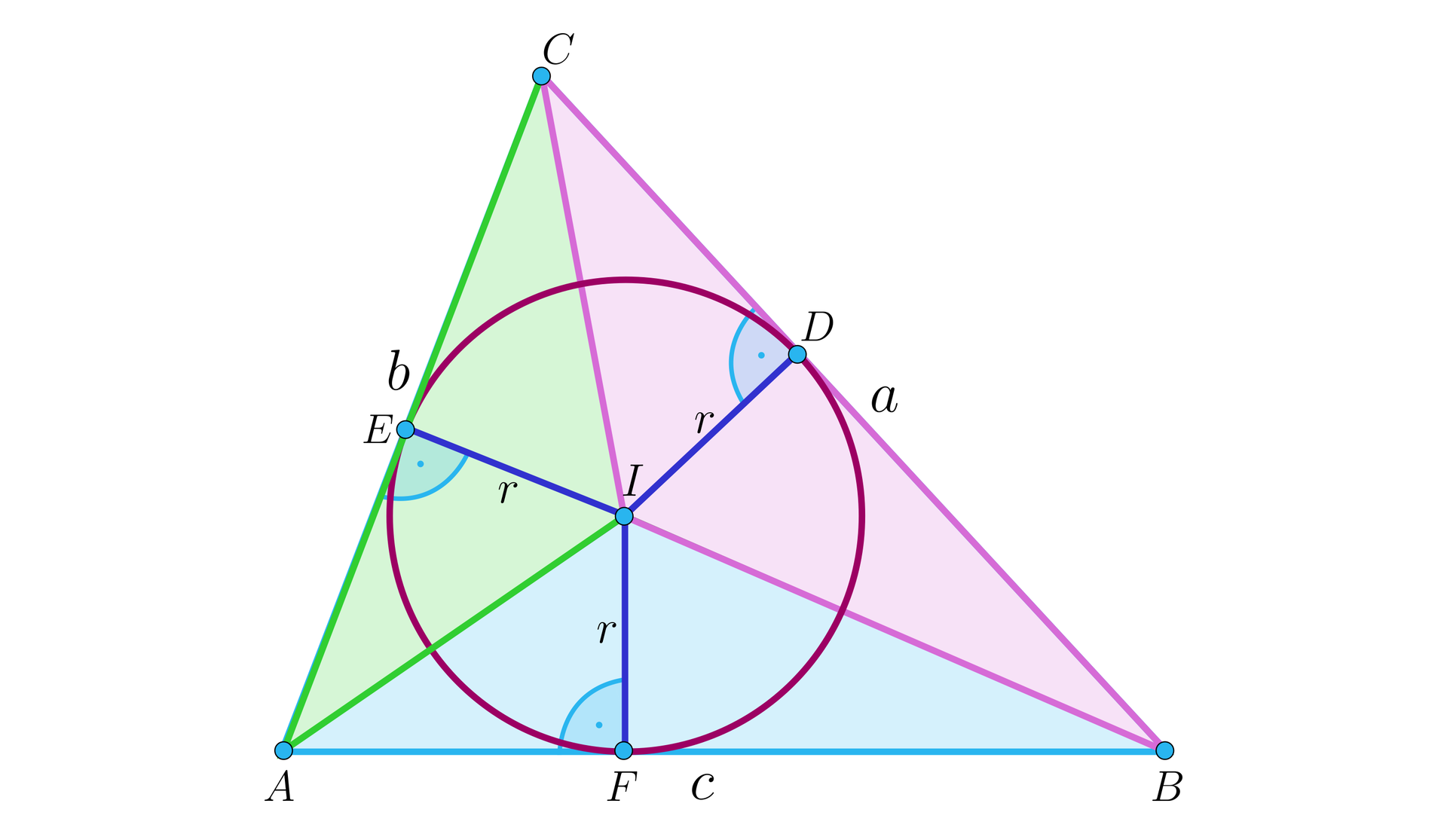
Ilustracja przedstawia trójkąt A B C, w który wpisano okrąg, środek okręgu zaznaczono literą I. Punkty styczne trójkąta i okręgu są następujące: na boku BC leży punkt D, na boku AC leży punkt E, na boku AB leży punkt F. Odcinki: DI, EI i FI są podpisane literą r. Bok BC podpisano literą a, bok AC podpisano literą b, bok AB podpisano literą c. W trójkącie A B C zaznaczono trzy trójkąty: AIC, AIB oraz BIC.

Widzimy, że pole trójkąta $A B C$ jest sumą pól trzech zaznaczonych trójkątów. Zatem:

$P = P_{Δ A B I} + P_{Δ B C I} + P_{Δ C A I} = \frac{1}{2} c \cdot r + \frac{1}{2} a \cdot r + \frac{1}{2} b \cdot r = \frac{1}{2} (a + b + c) \cdot r$ .

$P = p \cdot r$ , gdzie $p$ to połowa obwodu.

Ważne!

Powyższy wzór jest prawdziwy dla dowolnego wielokąta opisanego na okręgu o promieniu $r$ .

Szczególne przypadki trójkąta

Przykład 1

Wyznaczymy długość promienia okręgu wpisanego w trójkąt równobocznytrójkąt równobocznytrójkąt równoboczny o boku długości $a$ .

R1XWHq7KURIQC

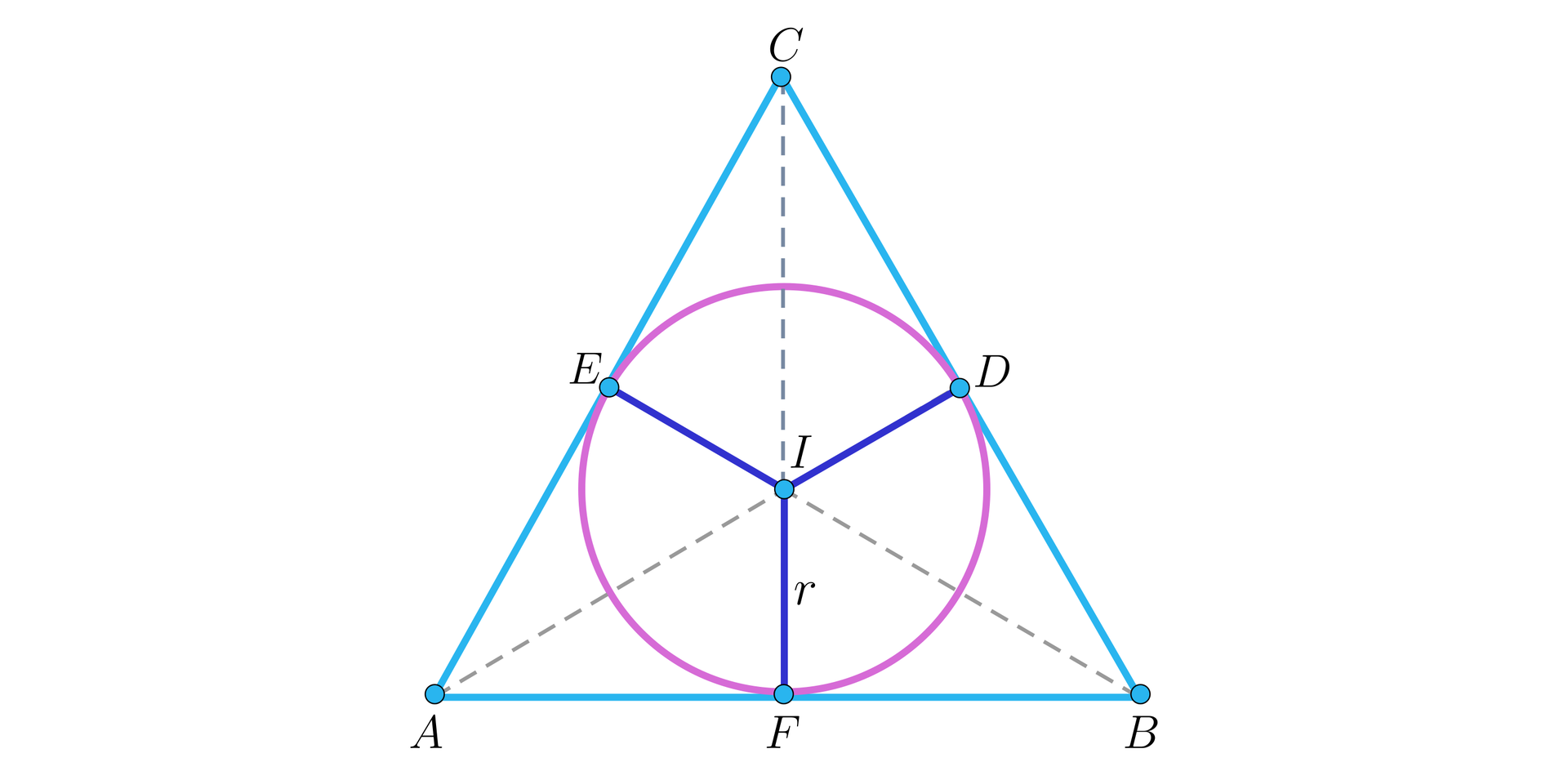
Rozwiązanie

W trójkącie równobocznymtrójkąt równobocznytrójkącie równobocznym proste zawierające dwusieczne pokrywają się z prostymi zawierającymi środkowe, więc punkt przecięcia dwusiecznych dzieli odcinki dwusiecznychdwusieczna kąta w trójkąciedwusiecznych w stosunku $2 : 1$ licząc od wierzchołka trójkąta.

Jednocześnie, w trójkącie równobocznymtrójkąt równobocznytrójkącie równobocznym proste zawierające dwusieczne pokrywają się z prostymi zawierającymi wysokość, więc łatwo wyznaczyć ich długości.

Otrzymujemy:

$r = \frac{1}{3} h = \frac{1}{3} \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{6}$ .

Przykład 2

Wyznaczymy długość promienia okręgu wpisanego w trójkąt równoramiennytrójkąt równoramiennytrójkąt równoramienny o podstawie długości $|A B| = a$ i ramionach długości $|B C| = |C A| = b$ .

Rozwiązanie

Przyjmujemy oznaczenia jak na rysunku:

R1Z4DeWlAXTMt

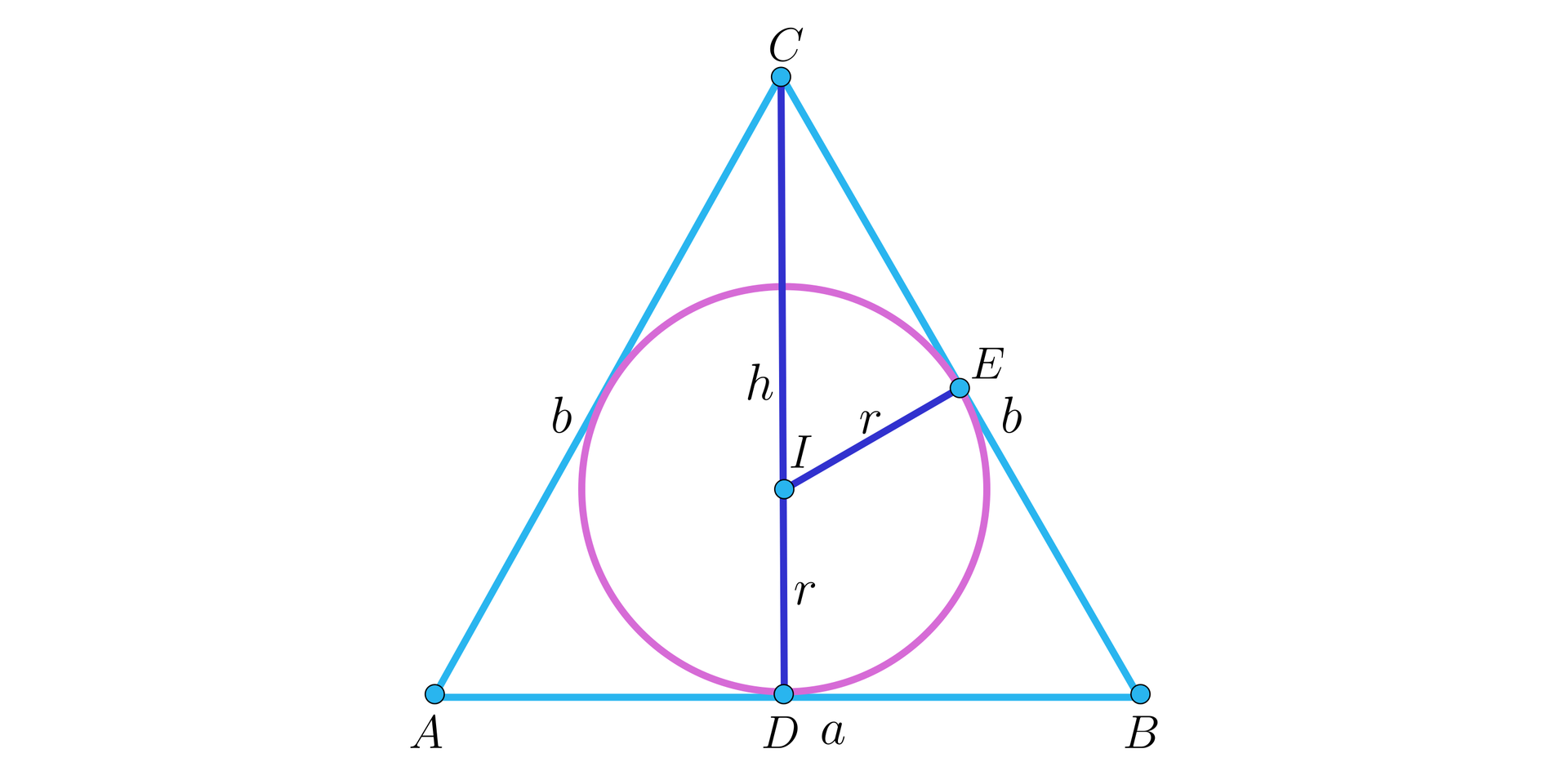
Ilustracja przedstawia trójkąt A B C, w który wpisano okrąg, środek okręgu zaznaczono literą I. Na boku BC zaznaczono punkt E. Na boku AB zaznaczono punkt D. Odcinek CD jest wysokością i podpisano go literą h. Odcinek ID podpisano literą r, odcinek IE również podpisano literą r. Bok AB podpisano literą a, boki AC oraz BC podpisano literą b.

Z twierdzenia Pitagorasa możemy obliczyć długość wysokości trójkąta:

$h = \sqrt{b^{2} - {(\frac{a}{2})}^{2}} = \frac{\sqrt{4 b^{2} - a^{2}}}{2}$ .

Mamy długości wszystkich boków i wysokości, zatem możemy obliczyć połowę obwodu i pole trójkąta, a więc i długość promienia okręgu wpisanego:

$P = p r$

$\frac{1}{2} a h = \frac{1}{2} (a + 2 b) r$

$r = \frac{a h}{a + 2 b} = \frac{a \frac{\sqrt{4 b^{2} - a^{2}}}{2}}{a + 2 b} = \frac{a \sqrt{4 b^{2} - a^{2}}}{2 a + 4 b}$ .

Uwaga! Gdy zauważymy, że trójkąt $I C E$ jest podobny do „połowy” trójkąta równoramiennegotrójkąt równoramiennytrójkąta równoramiennego $A B C$ i zapiszemy odpowiednią proporcję boków, np.:

$\frac{r}{\frac{a}{2}} = \frac{h - r}{b}$ ,

to po przekształceniu również otrzymujemy

$r = \frac{a h}{a + 2 b}$ .

Przykład 3

Wyznaczymy teraz dwoma sposobami wzór na długość promienia okręgu wpisanego w trójkąt prostokątnytrójkąt prostokątnytrójkąt prostokątny o przyprostokątnych długości $a$ i $b$ .

Rozwiązanie

Sposób 1:

Wiemy, z twierdzenia Pitagorasa, że $c = \sqrt{a^{2} + b^{2}}$ . Możemy więc obliczyć pole i obwód trójkąta, czyli korzystając ze wzoru $P = p \cdot r$ , otrzymujemy:

$r = \frac{P}{p} = \frac{\frac{1}{2} a b}{\frac{1}{2} (a + b + c)} = \frac{a b}{a + b + c}$ .

Sposób 2:

Przyjmijmy oznaczenia jak na rysunku:

R192ZTOMsqk6g

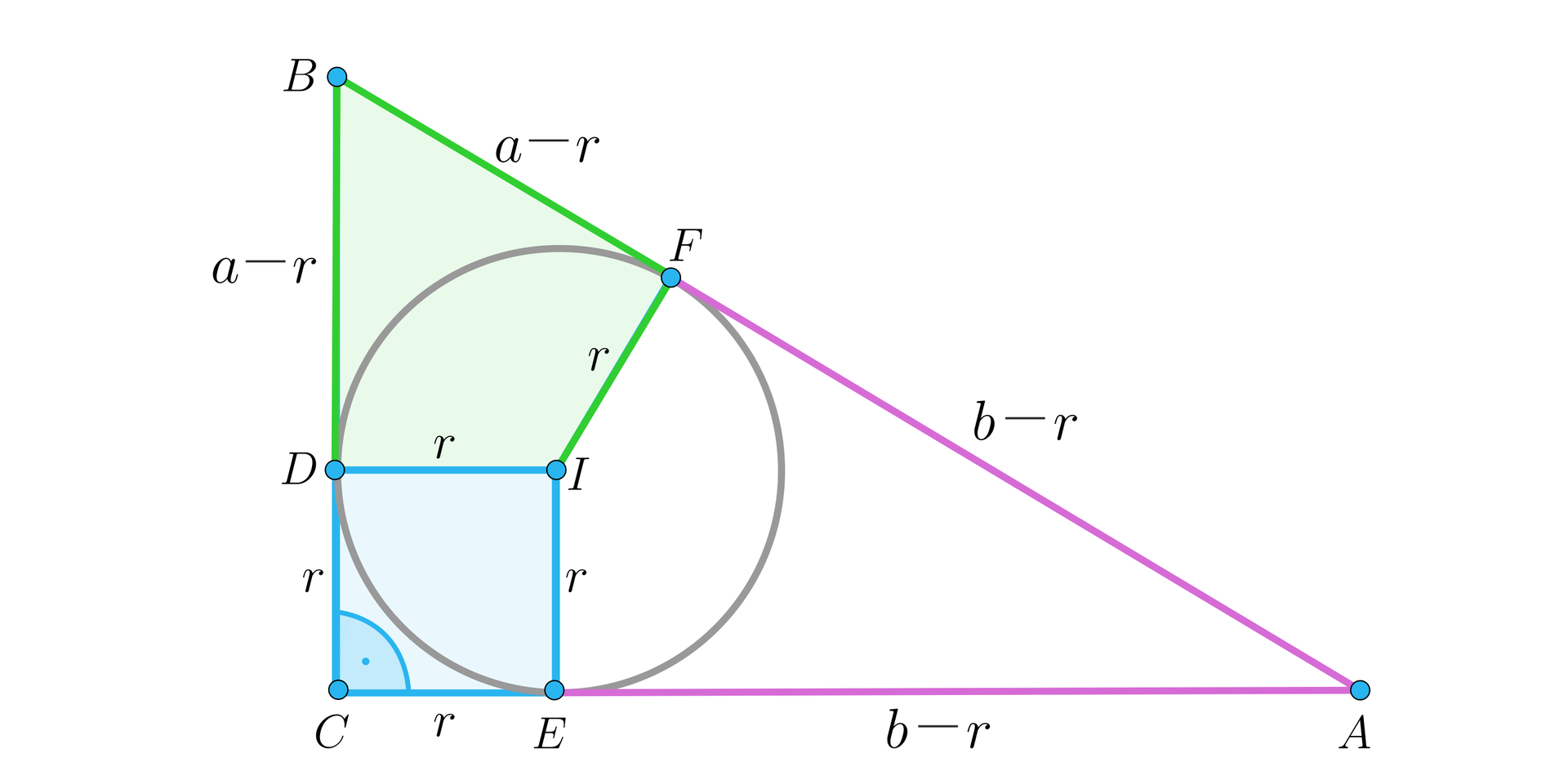
Ilustracja przedstawia trójkąt prostokątny A B C, w który wpisano okrąg, środek okręgu zaznaczono literą I. AB jest przeciwprostokątną. Punkty styczne trójkąta i okręgu są następujące: na boku BC leży punkt D, na boku AC leży punkt E, na boku AB leży punkt F. Odcinki: DI, EI i FI są podpisane literą r. Odcinki CD o CE mają długość r. Odcinek AE ma długość b minus r, odcinek BD ma długość a minus r, odcinek FB ma długość a minus r, a odcinek AF ma długość b minus r.

Z twierdzenia o odcinkach stycznych $|C E| = |C D|$ , ponadto kąt przy wierzchołku $C$ jest prosty oraz proste $I E$ i $I D$ są prostopadłe do przyprostokątnych. Zatem czworokąt $C E I D$ jest kwadratem o boku długości $r$ . Podobnie, z twierdzenia o odcinkach stycznych otrzymujemy $|B F| = |B D| = a - r$ oraz $|A F| = |A E| = b - r$ . Wiemy, że $|A F| + |F B| = c$ , zatem:

$a - r + b - r = c$

$2 r = a + b - c$

$r = \frac{a + b - c}{2}$ .

Sprawdzimy teraz, że wzory z pierwszego i drugiego sposobu wyznaczają tę samą wartość. W tym celu przekształcimy równoważnie równość:

$\frac{a + b - c}{2} = \frac{a b}{a + b + c}$

$(a + b - c) (a + b + c) = 2 a b$

${(a + b)}^{2} - c^{2} = 2 a b$

$a^{2} + b^{2} + 2 a b^{2} - c^{2} = 2 a b$

$a^{2} + b^{2} = c^{2}$ .

Ostatnia równość jest oczywiście prawdziwa w przypadku trójkąta prostokątnegotrójkąt prostokątnytrójkąta prostokątnego, więc tym samym wykazaliśmy, że wzory z pierwszego i drugiego sposobu wyznaczają tę samą wartość.

Na koniec dwa ciekawe przykłady związane z zagadnieniem okręgu wpisanego w trójkąt.

Przykład 4

Przez środek $I$ okręgu wpisanego w trójkąt $A B C$ poprowadzono prostą równoległą do boku $A B$ , która przecina boki $C A$ i $C B$ odpowiednio w punktach $E$ i $D$ . Wykażemy, że: $|E D| = |E A| + |D B|$ .

R1Rwbqk4oFmyA

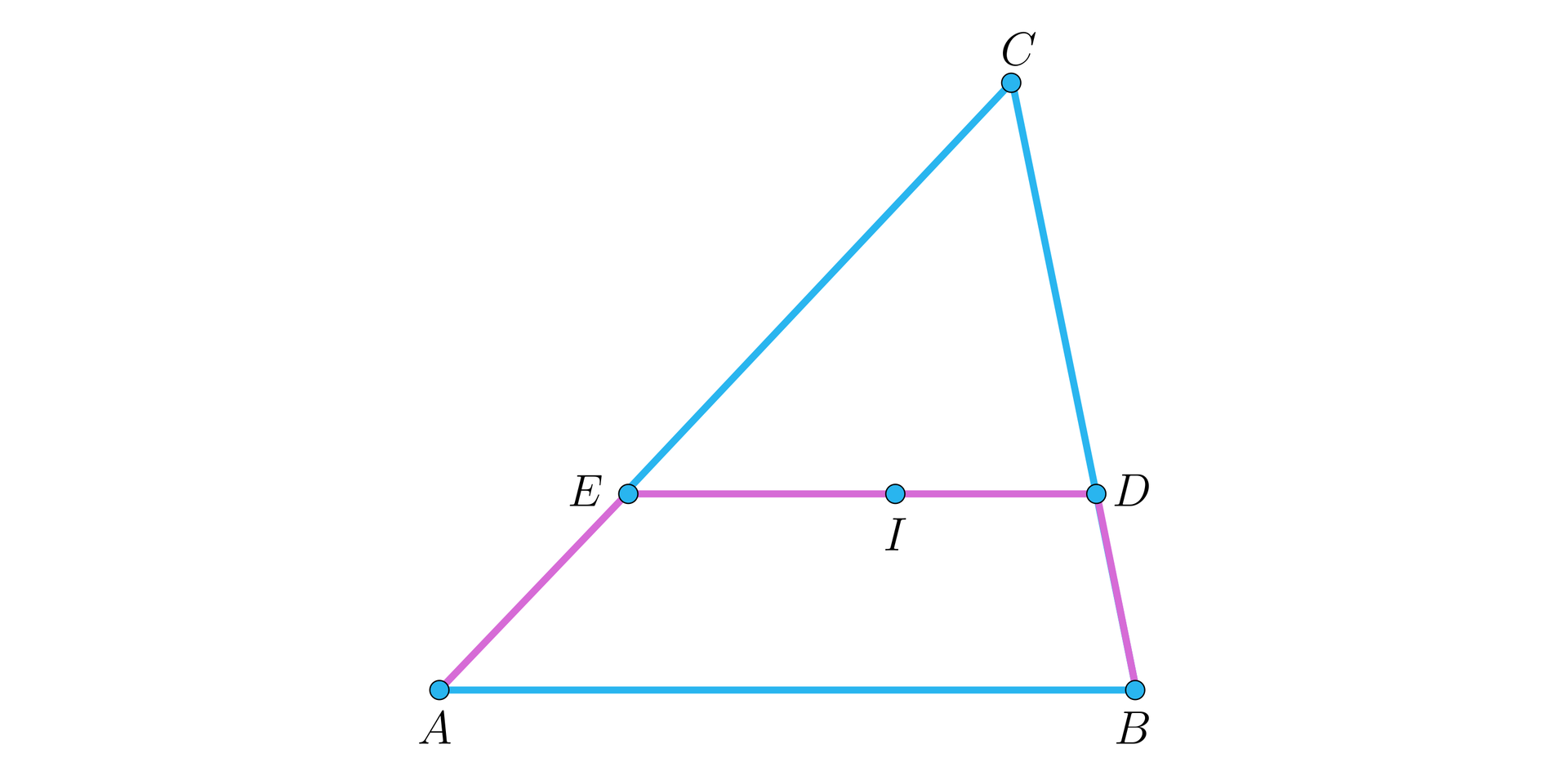
Ilustracja przedstawia trójkąt prostokątny A B C, na boku AC zaznaczono punkt D, na boku BC zaznaczono punkt D. W trójkącie zaznaczono odcinek ED, na którym leży punkt I. Odcinki AE, ED oraz Db zaznaczono kolorem.

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku:

R101p09w4J4YU

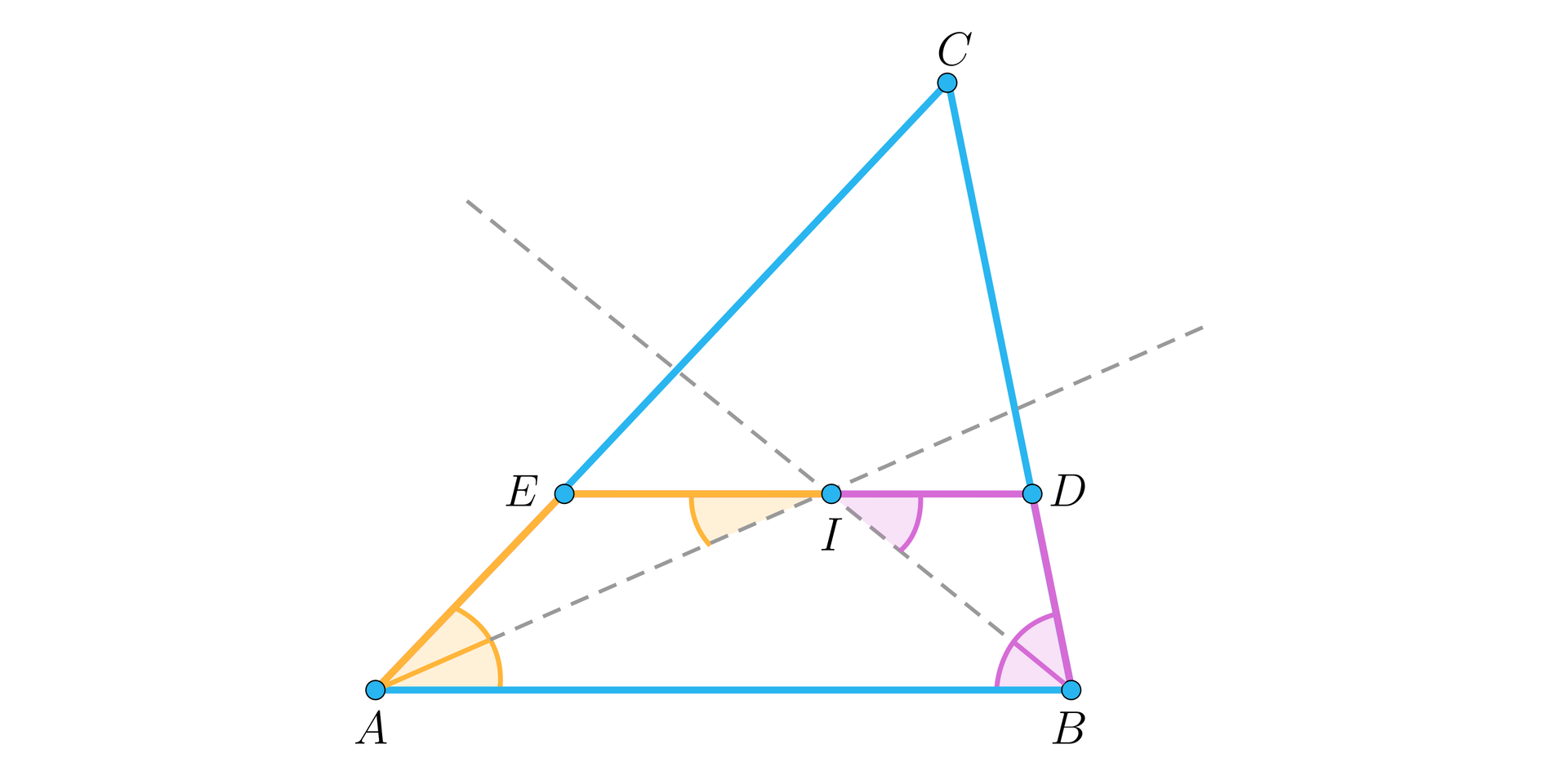
Środek okręgu wpisanego $I$ leży w punkcie przecięcia dwusiecznych, stąd wnioskujemy równość miar kątów: $|∢ E A I| = |∢ I A B|$ oraz $|∢ D B I| = |∢ I B A|$ . Wiemy, z założeń zadania, że proste $E D$ i $A B$ są równoległe, więc mamy też równość kątów naprzemianległych: $|∢ I A B| = |∢ A I E|$ oraz $|∢ I B A| = |∢ B I D|$ . Z poprzednich równości otrzymujemy równość kątów $|∢ E A I| = |∢ E I A|$ oraz $|∢ D B I| = |∢ D I B|$ . Trójkąty $A E I$ i $B D I$ są zatem równoramienne.

$|E D| = |E I| + |I D| = |A E| + |D B|$ .

Przykład 5

W trójkąt prostokątnytrójkąt prostokątnytrójkąt prostokątny $A B C$ o przyprostokątnych długości $|A C| = 3$ i $|B C| = 4$ wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków $A B$ i $B C$ , a drugi do boków $A C$ i $B C$ .

RHfAfxp82W6U3

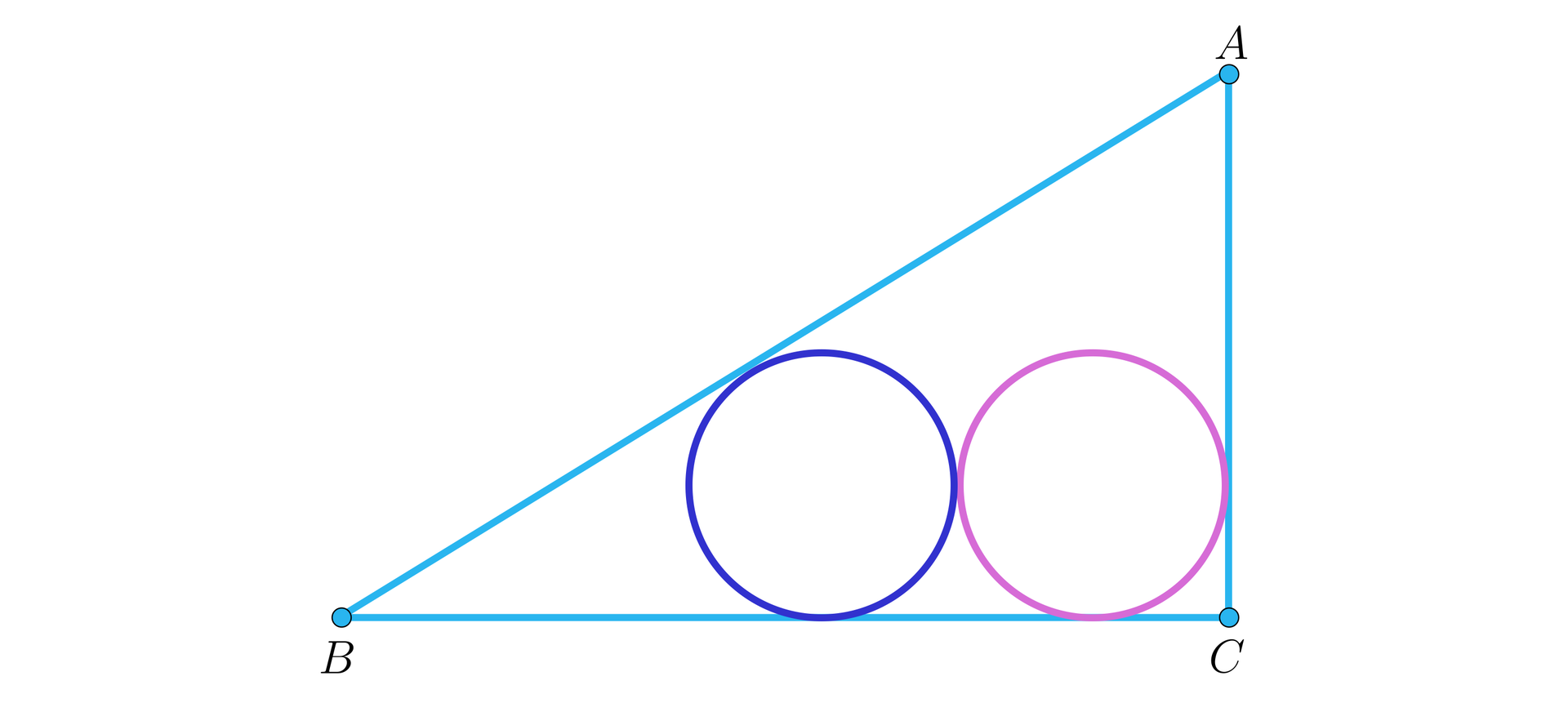
Ilustracja przedstawia trójkąt prostokątny A B C, w którym znajdują się dwa styczne do siebie okręgi. Jeden okrąg jest styczny do boków AC i BC, a drugi jest styczny do boków AB i BC.

Obliczymy długość promienia tych okręgów.

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku:

R1OYNJ7Z5grTK

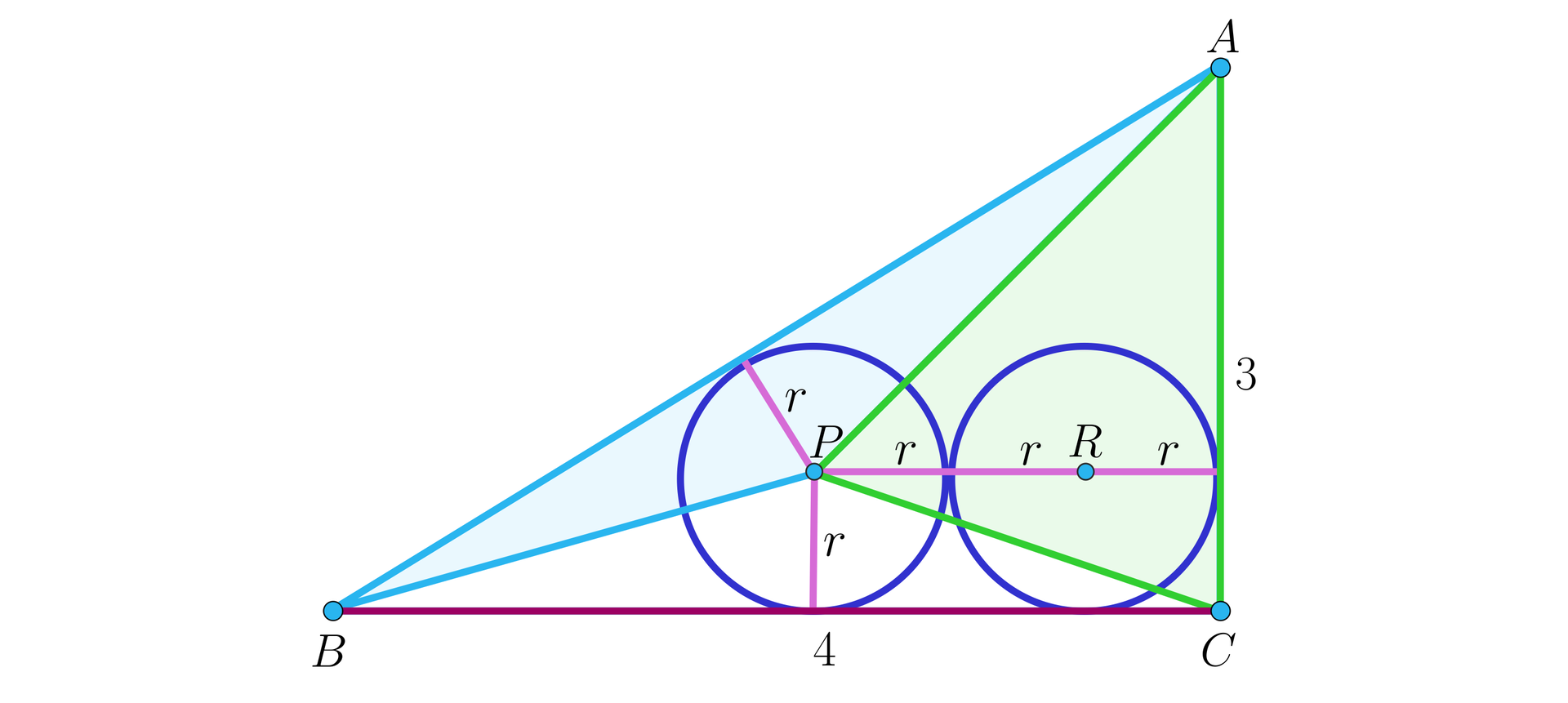
Połączmy środek $P$ jednego z okręgów z wierzchołkami. Otrzymujemy trzy trójkąty. Suma pól tych trójkątów to pole trójkąta $A B C$ :

$P_{Δ A B C} = P_{Δ A B P} + P_{Δ B C P} + P_{Δ C A P}$

$\frac{1}{2} \cdot 4 \cdot 3 = \frac{1}{2} \cdot 5 \cdot r + \frac{1}{2} \cdot 4 \cdot r + \frac{1}{2} \cdot 3 \cdot 3 r$

$6 = \frac{5}{2} r + 2 r + \frac{9}{2} r$

$6 = 9 r$

$r = \frac{2}{3}$ .

Słownik

trójkąt równoboczny

trójkąt, którego wszystkie boki mają taką samą długość. Jest to szczególny przypadek trójkąta równoramiennego. Jest przykładem wielokąta foremnego

trójkąt równoramienny

trójkąt o (co najmniej) dwóch bokach równej długości. Te dwa boki nazywane są ramionami trójkąta, trzeci bok podstawą. Kąty przy podstawie są przystające a ich miara jest mniejsza od miary kąta prostego

trójkąt prostokątny

trójkąt, którego jeden z kątów wewnętrznych jest prosty. Dwa boki trójkąta wyznaczające ramiona kąta prostego nazywane są przyprostokątnymi, trzeci bok przeciwprostokątną

dwusieczna kąta

zbiór punktów płaszczyzny leżących w równej odległości od ramion kąta płaskiego

dwusieczna kąta w trójkącie

odcinek będący częścią wspólną dwusiecznej kąta trójkąta i trójkąta

Wprowadzenie

Symulacja interaktywna

W każdy trójkąt można wpisać okrąg

Pole trójkąta opisanego na okręgu o promieniu $r$

Szczególne przypadki trójkąta

Słownik

Wprowadzenie

Symulacja interaktywna

Przeczytaj

W każdy trójkąt można wpisać okrąg

Pole trójkąta opisanego na okręgu o promieniu r

Szczególne przypadki trójkąta

Słownik

Pole trójkąta opisanego na okręgu o promieniu $r$