Przeczytaj

Zacznijmy od pary prostych, z których żadna nie jest równoległa do osi $Y$ , czyli można je opisać równaniami kierunkowymi $y = a x + b$ i $y = c x + d$ . Wówczas współrzędne ich punktu wspólnego możemy wyznaczyć rozwiązując układ równań

\{\begin{array}{l} y = a x + b \\ y = c x + d \end{array},

z którego wynika równanie

a x + b = c x + d

(a - c) x = d - b

Zauważmy, że jeśli $a - c = 0$ , to $a = c$ , więc proste są równoległe, co oznacza, że albo nie mają punktów wspólnych, albo mają ich nieskończenie wiele. Jeśli zaś $a - c \neq 0$ , to

x = \frac{d - b}{a - c} .

Po podstawieniu do pierwszego równania powyższej równości, możemy wyznaczyć $y$ . Istotnie

y = a \cdot \frac{d - b}{a - c} + b = \frac{a d - a b}{a - c} + \frac{b a - b c}{a - c} = \frac{a d - b c}{a - c}

Zatem punkt przecięcia prostychpunkt przecięcia prostychpunkt przecięcia prostych ma współrzędne

(\frac{d - b}{a - c}, \frac{a d - b c}{a - c})

R1LDQISbkj779

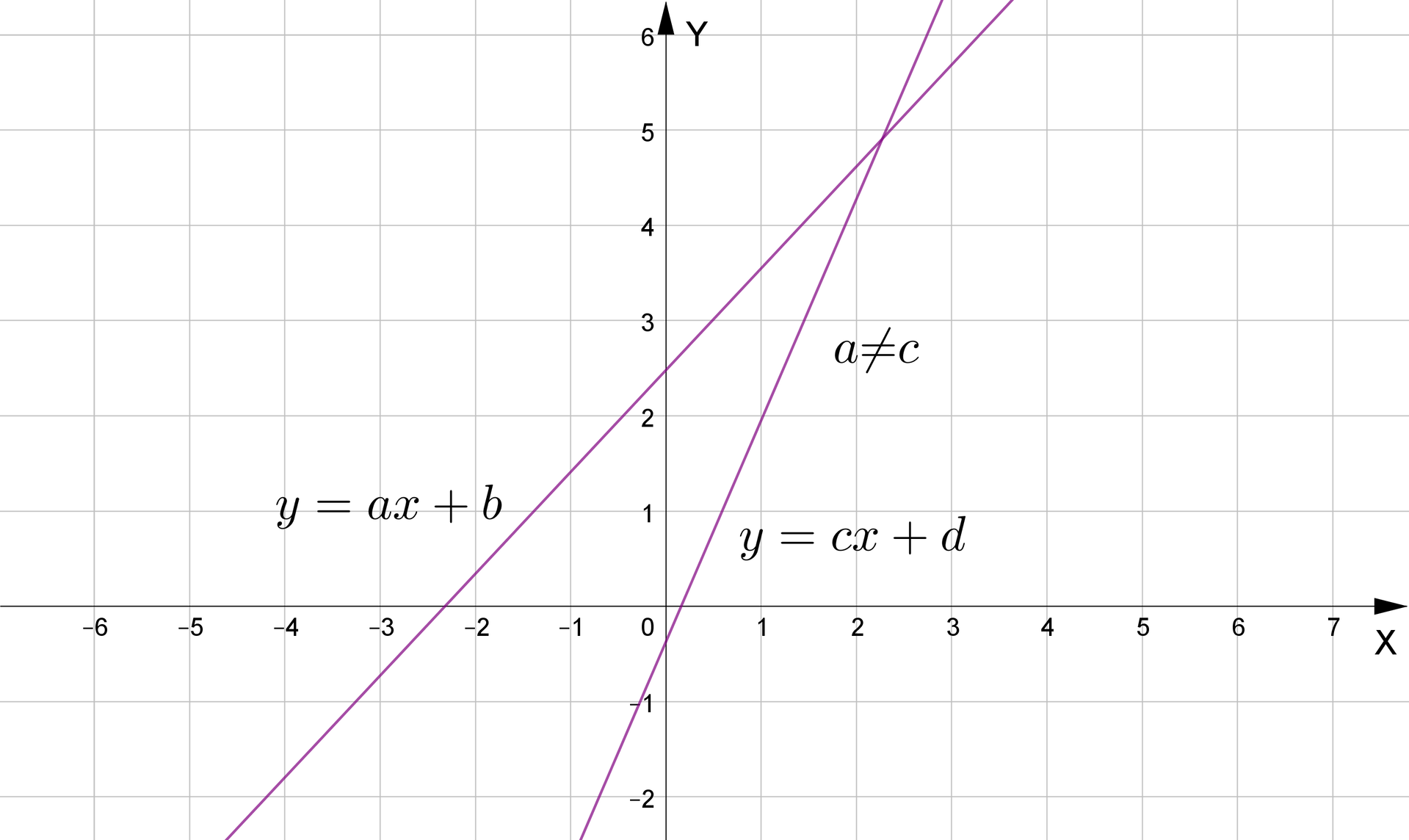
Ilustracja przedstawia układ współrzędnych z poziomą osią X od -6 do 7 oraz z pionową osią Y od -2 do sześć. Narysowano dwie ukośne proste o równaniach y=ax+b oraz y=cx+d, gdzie a≠c. Proste przecinają się ze sobą w pierwszej ćwiartce układu współrzędnych.

Analogiczną analizę możemy przeprowadzić dla prostych opisanych równaniami ogólnymi, które obejmują również proste równoległeproste równoległeproste równoległe do osi $Y$ . Aby wyznaczyć punkt wspólny prostych o równaniach $A x + B y + C = 0$ , gdzie $A$ i $B$ nie są jednocześnie równe zeru, oraz $D x + E y + F = 0$ , gdzie $D$ i $E$ nie są jednocześnie równe zeru, wystarczy rozwiązać układ równań

\{\begin{cases} A x + B y + C = 0 \\ D x + E y + F = 0 \end{cases}

\{\begin{cases} A x + B y = - C \\ D x + E y = - F \end{cases}

Po pomnożeniu pierwszego równania przez $D$ , zaś drugiego przez $A$ , otrzymujemy równania

\{\begin{cases} A D x + B D y = - C D \\ A D x + A E y = - A F \end{cases}

Po odjęciu stronami drugiego równania od pierwszego otrzymujemy równanie z niewiadomą $y$ :

(B D - A E) y = A F - C D

Analogiczne równanie możemy otrzymać dla niewiadomej $x$ :

(B D - A E) x = C E - B F

Zwróćmy uwagę, że jeśli $B D - A E = 0$ , to powyższe równania są sprzeczne albo tożsamościowe, więc rozważane proste nie przecinają się w jednym punkcie. Jeśli zaś $B D - A E \neq 0$ , to każde z równań możemy obustronnie podzielić przez wyrażenie $B D - A E$ , co prowadzi do otrzymania współrzędnych punktu przecięcia

(x, y) = (\frac{C E - B F}{B D - A E}, \frac{A F - C D}{B D - A E})

RaLYGXNQITs40

Ilustracja przedstawia układ współrzędnych z poziomą osią X od -6 do 6 oraz z pionową osią Y od -2 do pięć. Narysowano dwie ukośne proste o równaniach ogólnych: Ax+By+C=0 oraz Dx+Ey+F=0, gdzie BD-AE≠0. Proste przecinają się w trzeciej ćwiartce układu współrzędnych.

Czasami współrzędne punktu przecięcia dwóch prostych możemy odczytać z rysunku, jednak warto wtedy zachować ostrożność. Przede wszystkim współrzędne punktu przecięcia prostych odczytujemy z rysunku tylko wtedy, gdy są one liczbami całkowitymi, czyli punkt przecięcia prostychpunkt przecięcia prostychpunkt przecięcia prostych jest punktem kratowym. Warto też sprawdzić odczytane współrzędne podstawiając je do równań prostych.

Przykład 1

Wyznaczymy punkt wspólny prostych o równaniach $y = \frac{2}{3} x + \frac{3}{2}$ i $y = - \frac{1}{3} x - \frac{4}{3}$ .

R18184ZETRKyV

Ilustracja przedstawia układ współrzędnych z poziomą osią X od -6 do sześć oraz z pionową osią Y od -2 do pięć. W układzie współrzędnych narysowano dwie proste o równaniach: y=23x+32 oraz y=-13x-43.

W tym celu rozwiążemy układ równań:

\{\begin{matrix} y = \frac{2}{3} x + \frac{3}{2} \\ y = - \frac{1}{3} x - \frac{4}{3} \end{matrix}

z którego wynika równanie

\frac{2}{3} x + \frac{3}{2} = - \frac{1}{3} x - \frac{4}{3}

Można je rozwiązać następująco

4 x + 9 = - 2 x - 8

6 x = - 17

x = - \frac{17}{6}

Zatem rozwiązaniem układu jest para liczb

\{\begin{cases} x = - \frac{17}{6} \\ y = \frac{2}{3} \cdot (- \frac{17}{6}) + \frac{3}{2} = - \frac{7}{18} \end{cases}

Punkt przecięcia danych prostych ma współrzędne $(- \frac{17}{6}; - \frac{7}{18})$ . Zauważmy, że trudno byłoby je odczytać z rysunku.

Przykład 2

Wyznaczymy współrzędne punku wspólnego prostych o równaniach $x = 3$ oraz $4 x - 2 y = - 1$ . Aby wyznaczyć współrzędne punktu wspólnego tych prostych, wystarczy rozwiązać układ równań

\{\begin{cases} x = 3 \\ 4 x - 2 y = - 1 \end{cases}

z którego wynika równanie

4 \cdot 3 - 2 y = - 1

Przekształcając je, otrzymamy $y$

- 2 y = - 1 - 12

y = 6, 5

Zatem współrzędne punktu wspólnego danych prostych to $(3; 6, 5)$ .

RVsZLrd4CNGQK

Ilustracja przedstawia układ współrzędnych z poziomą osią X od -10 do dziesięć oraz z pionową osią Y od -3 do osiem. W układzie współrzędnych narysowano dwie proste: x=3 oraz 4x-2y=-1. Zaznaczono punkt przecięcia tych prostych. Ma on współrzędne: 3;6,5.

Przykład 3

Punkt $A = (- 6, 1)$ jest wierzchołkiem trójkąta $A B C$ , a punkt $D$ jest środkiem odcinka $A B$ . Równania prostych $A B$ , $C D$ oraz symetralnej boku $B C$ to odpowiednio

y = \frac{1}{2} x + 4

y = - \frac{7}{4} x - 5

y = x + 11

Wyznaczymy równanie prostej zawierającej wysokość trójkąta $A B C$ opuszczoną z wierzchołka $C$ . Zaczniemy od wyznaczenia współrzędnych punktu $D$ , rozwiązując układ równań

\{\begin{cases} y = \frac{1}{2} x + 4 \\ y = - \frac{7}{4} x - 5 \end{cases}

z którego wynika równanie

\frac{1}{2} x + 4 = - \frac{7}{4} x - 5

Wykonując kolejne przekształcenia otrzymujemy:

2 x + 16 = - 7 x - 20

9 x = - 36

więc

x = - 4

Pozostaje wyznaczyć niewiadomą $y$ :

\{\begin{cases} x = - 4 \\ y = \frac{1}{2} \cdot (- 4) + 4 \end{cases}

\{\begin{cases} x = - 4 \\ y = 2 \end{cases}

Zatem punkt $D$ ma współrzędne $(- 4, 2)$ . Współrzędne punktu $B (x_{B}, y_{B})$ możemy wyznaczyć, korzystając ze wzorów na współrzędne środka odcinka o danych końcach:

\frac{x_{B} - 6}{2} = - 4

\frac{y_{B} + 1}{2} =2

Zatem współrzędne punktu $B$ to $(- 2, 3)$ . Ponieważ prosta $B C$ jest prostopadła do prostej o równaniu $y = x + 11$ , więc jej współczynnik kierunkowy jest równy $(- 1)$ . Wykorzystując współrzędne punktu $B$ możemy wyznaczyć równanie prostej $B C$ :

y = - (x + 2) + 3

y = - x + 1

Współrzędne punktu $C$ , możemy wyznaczyć rozwiązując układ równań

\{\begin{cases} y = - x + 1 \\ y = - \frac{7}{4} x - 5 \end{cases}

Zatem punkt $C$ ma współrzędne $(- 8, 9)$ . Współczynnik kierunkowy prostej zawierającej wysokość poprowadzoną z wierzchołka $C$ to $(- 2)$ , więc jej równanie to

y = - 2 (x + 8) + 9

y = - 2 x - 7

Słownik

proste równoległe

w geometrii euklidesowej są to proste, które nie mają punktów wspólnych; wg Euklidesa są to proste, które przecięte trzecią prostą tworzą z nią kąty wewnętrzne po jednej jej stronie o miarach, których suma jest równa $180 °$

punkt przecięcia prostych

punkt wspólny dwóch różnych prostych

Wprowadzenie

Film samouczek

Słownik