Przeczytaj

Jeżeli mamy dany trójkąt, z oznaczeniami długości boków i miar kątów, jak na poniższym rysunku, to jego pole możemy wyznaczyć za pomocą różnych wzorów.

RntoAjjPsN7mR

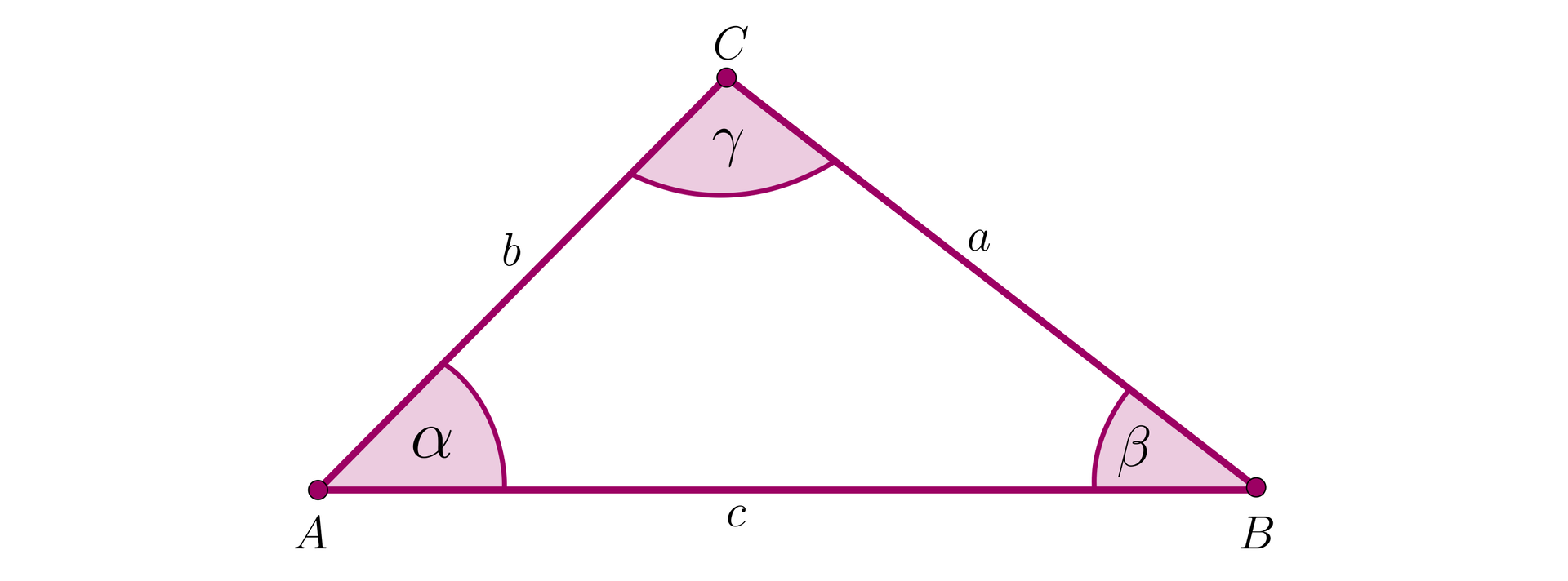
Ilustracja przedstawia trójkąt A B C z zaznaczonymi kątami alfa, beta oraz gamma. Pierwszy, kąt alfa znajduje się przy wierzchołku B, kąt beta znajduje się przy wierzchołku B, natomiast kąt gamma znajduje się przy wierzchołku C. Na rysunku zaznaczono także odpowiednie długości odcinków, odcinek A B o długości c, odcinek B C o długości a oraz odcinek A C o długości b.

Przyjmijmy następujące oznaczenia:

$a, b, c$ – długości boków, leżących odpowiednio naprzeciwko wierzchołków $A, B, C$ ,

$2 p = a + b + c$ – obwód trójkąta,

$α, β, γ$ – miary kątów przy wierzchołkach $A, B, C$ ,

$h_{a}, h_{b}, h_{c}$ – wysokości opuszczone z wierzchołków $A, B, C$

$R, r$ – promienie okręgów opisanego i wpisanego.

Zatem:

P = \frac{1}{2} \cdot a \cdot h_{a} = \frac{1}{2} \cdot b \cdot h_{b} = \frac{1}{2} \cdot c \cdot h_{c}

P = \frac{1}{2} \cdot a \cdot b \cdot \sin γ = \frac{1}{2} \cdot a \cdot c \cdot \sin β = \frac{1}{2} \cdot b \cdot c \cdot \sin α

P = \sqrt{p \cdot (p - a) \cdot (p - b) \cdot (p - c)}

P = r \cdot p

Przypomnijmy sformułowanie twierdzenia sinusówtwierdzenie sinusówtwierdzenia sinusów.

Twierdzenie sinusów (twierdzenie Snelliusa)

Twierdzenie: Twierdzenie sinusów (twierdzenie Snelliusa)

W dowolnym trójkącie na płaszczyźnie stosunki długości boków do sinusów przeciwległych kątów są równe i równają się średnicy okręgu opisanego na tym trójkącie:

\frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ} = 2 R

RCOPj88NRuGL4

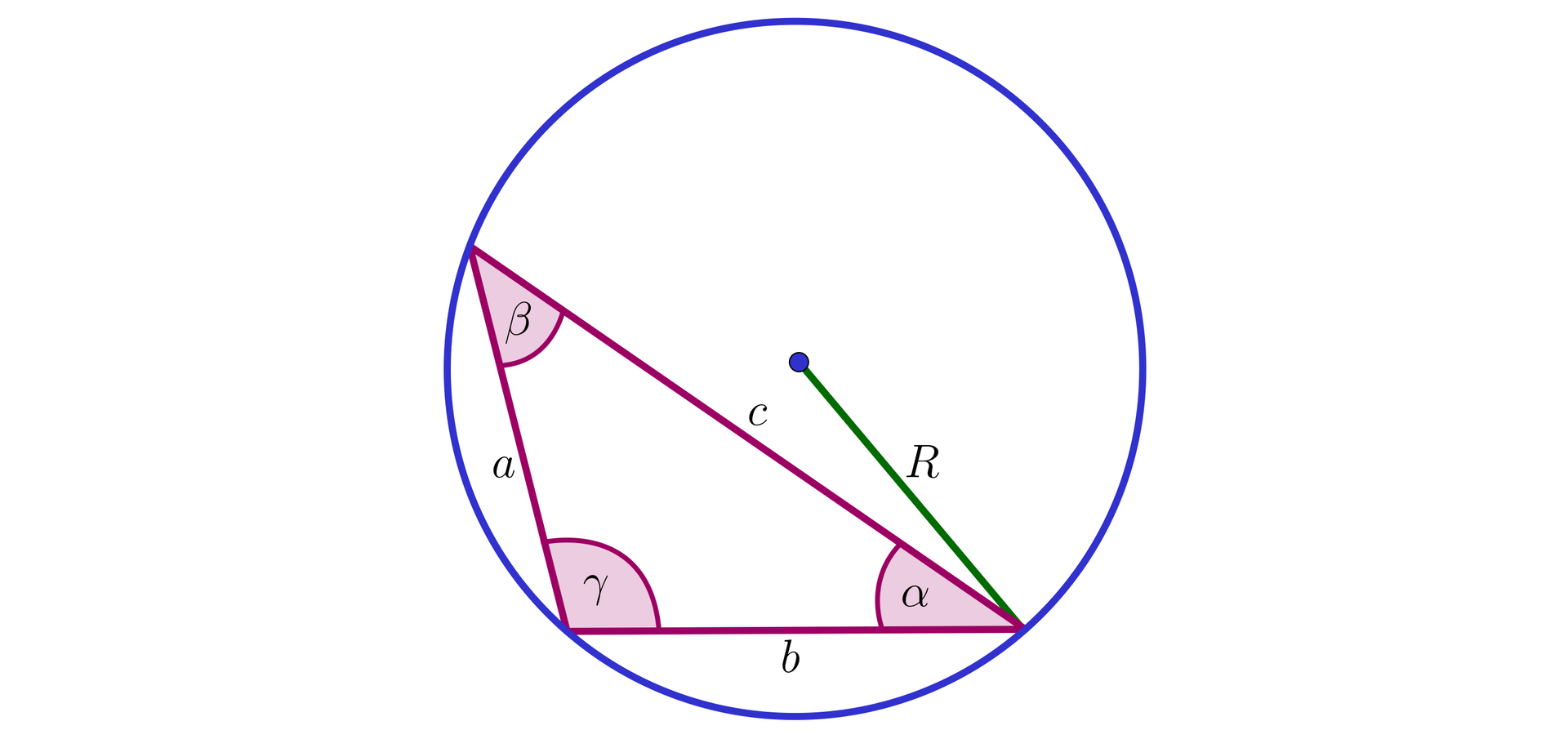
Ilustracja przedstawia trójkąt rozwartokątny wpisany w okrąg. Boki trójkąta podpisano literami a b oraz c. Kąt pomiędzy bokami a i c podpisano literą beta. Kąt pomiędzy a i b podpisano literą gamma. Kąt pomiędzy b i c podpisano literą alfa. Ze środka okręgu do wierzchołka przy kącie alfa poprowadzono promień, który podpisano literą R.

Jak zastosować twierdzenie sinusów do obliczania pola trójkąta?

Jeżeli wiadomo, że $\frac{c}{\sin γ} = 2 R$ , to pole trójkątapole trójkątapole trójkąta możemy wyrazić za pomocą wzoru:
$P = \frac{1}{2} a b \cdot \sin γ = \frac{1}{2} a b \cdot \frac{c}{2 R} = \frac{a b c}{4 R}$

Jeżeli skorzystamy z zależności $\frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ}$ , to pole trójkąta można wyrazić za pomocą wzoru:
$P = \frac{1}{2} a^{2} \cdot \frac{\sin β \cdot \sin γ}{\sin α} = \frac{1}{2} b^{2} \cdot \frac{\sin α \cdot \sin γ}{\sin β} = \frac{1}{2} c^{2} \cdot \frac{\sin α \cdot \sin β}{\sin γ}$

Jeżeli skorzystamy z zależności $\frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ} = 2 R$ , to pole trójkąta możemy opisać za pomocą wzoru:
$P = 2 R^{2} \cdot \sin α \cdot \sin β \cdot \sin γ$

RlwIuzSb5zzSU

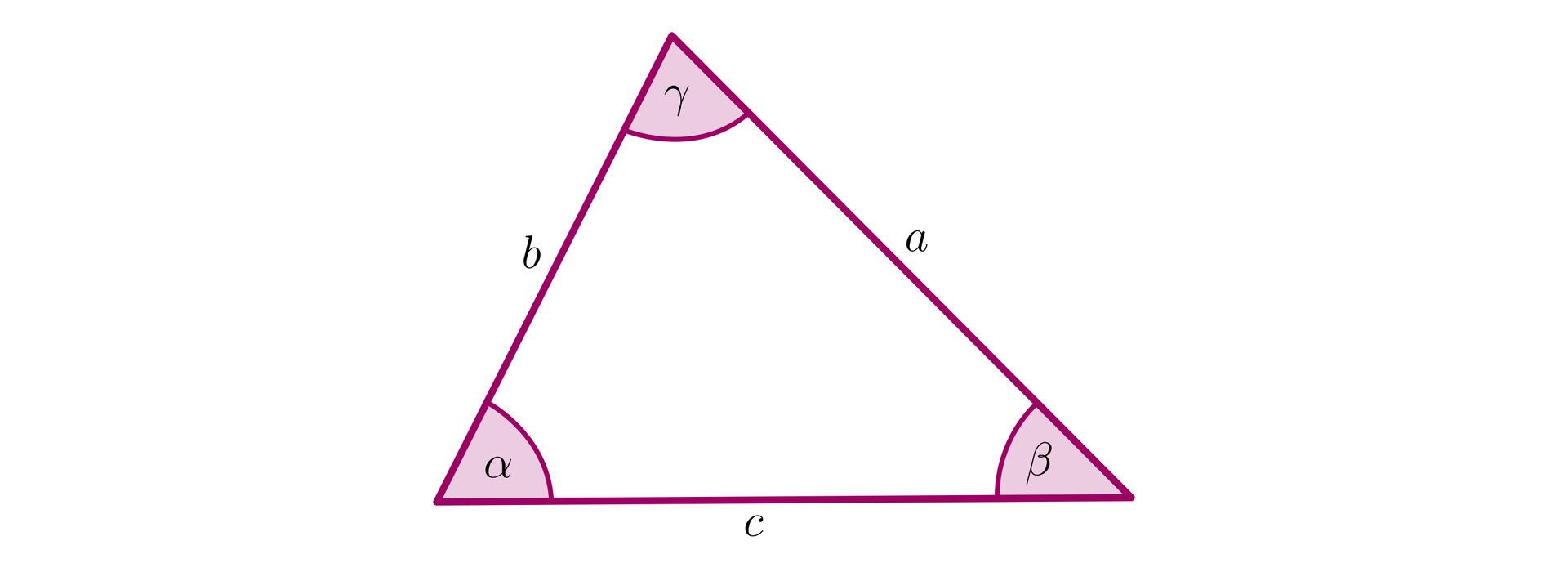
Ilustracja przedstawia trójkąt. Boki trójkąta podpisano literami a b oraz c. Kąt pomiędzy bokami a i c podpisano literą beta. Kąt pomiędzy a i b podpisano literą gamma. Kąt pomiędzy b i c podpisano literą alfa.

Pole trójkąta z rysunku obliczamy także za pomocą wzorów:

P = \frac{c^{2}}{2} \cdot \frac{tg α \cdot tg β}{tg α + tg β}

P = \frac{a^{2}}{4} \cdot (\sin 2 β + \frac{1 - \cos 2 β}{tg α})

Przykład 1

Obliczymy długość promienia okręgu opisanego na trójkącie, w którym pole jest równe $24$ , a iloczyn sinusów kątów wewnętrzynych tego trójkąta wynosi $\frac{3}{8}$ .

Rozwiązanie:

Niech $α$ , $β$ , $γ$ będą miarami kątów wewnętrznych w trójkącie.

Z warunków z zadania mamy, że:

$P = 24$ ,

$\sin α \cdot \sin β \cdot \sin γ = \frac{3}{8}$

Do wyznaczenia długości promienia okręgu opisanego wykorzystamy wzór $P = 2 R^{2} \cdot \sin α \cdot \sin β \cdot \sin γ$ .

Wobec tego:

$24 = 2 R^{2} \cdot \frac{3}{8}$

$R^{2} = \frac{96}{3}$ , czyli $R = \frac{\sqrt{96}}{\sqrt{3}} = \frac{4 \sqrt{6}}{\sqrt{3}} = 4 \sqrt{2}$

Przykład 2

Obliczymy pole trójkąta, gdy dane są wielkości $c = 8$ , $α = 45 °$ , $β = 30 °$ .

Rozwiązanie:

Do wyznaczenia wartości pola wykorzystamy wzór $P = \frac{c^{2}}{2} \cdot \frac{tg α \cdot tg β}{tg α + tg β}$ .

Zatem

$P = \frac{8^{2}}{2} \cdot \frac{tg 45 ° \cdot tg 30 °}{tg 45 ° + tg 30 °}$

$P = 32· \frac{1 \cdot \frac{\sqrt{3}}{3}}{1 + \frac{\sqrt{3}}{3}} = 32 \cdot \frac{\frac{\sqrt{3}}{3}}{\frac{3 + \sqrt{3}}{3}} = 32 \cdot \frac{\sqrt{3}}{3 + \sqrt{3}} = 32 \cdot \frac{\sqrt{3} \cdot (3 - \sqrt{3})}{(3 + \sqrt{3}) (3 - \sqrt{3})} =$

$= 32 \cdot \frac{3 \sqrt{3} - 3}{6} = 32 \cdot \frac{\sqrt{3} - 1}{2} = 16 \sqrt{3} - 16$

Przykład 3

Obliczymy miarę kąta leżącego naprzeciwko najkrótszego boku trójkąta, w którym boki mają długości $a = 8$ , $b = 10$ , $c = 12$ .

Rozwiązanie:

Do wyznaczenia miary szukanego kąta obliczymy najpierw długość promienia okręgu opisanego na trójkącie. W tym celu użyjemy wzoru na pole trójkąta $P = \frac{a b c}{4 R}$ .

Pole trójkąta obliczymy, korzystając ze wzoru Herona.

Zatem $p = \frac{8 + 10 + 12}{2} = 15$ .

Wobec tego pole trójkąta wynosi:

$P = \sqrt{15 \cdot (15 - 8) \cdot (15 - 10) \cdot (15 - 12)} = \sqrt{15 \cdot 7 \cdot 5 \cdot 3} = 15 \sqrt{7}$

Zatem do wyznaczenia długości promienia okręgu opisanego rozwiązujemy równanie:

$15 \sqrt{7} = \frac{8 \cdot 10 \cdot 12}{4 \cdot R}$

Długość promienia okręgu opisanego na tym trójkącie wynosi:

$R = \frac{16 \sqrt{7}}{7}$

Do wyznaczenia miary kąta leżącego naprzeciwko najkrótszego boku użyjemy twierdzenia sinusów.

Wobec tego:

$\frac{8}{\sin α} = 2 \cdot \frac{16 \sqrt{7}}{7}$

$\sin α = \frac{7}{4 \sqrt{7}} = \frac{\sqrt{7}}{4}$

Jeżeli wykorzystujemy tablice wartości funkcji trygonometrycznych, to $α \approx 42 °$ .

Przykład 4

Obliczymy pole trójkąta, w którym najdłuższy bok ma długość $12$ , a dwa kąty tego trójkąta mają miary $60 °$ i $45 °$ .

Rozwiązanie:

Narysujmy trójkąt i wprowadźmy oznaczenia, jak na poniższym rysunku.

R1LvCeQhw9wCI

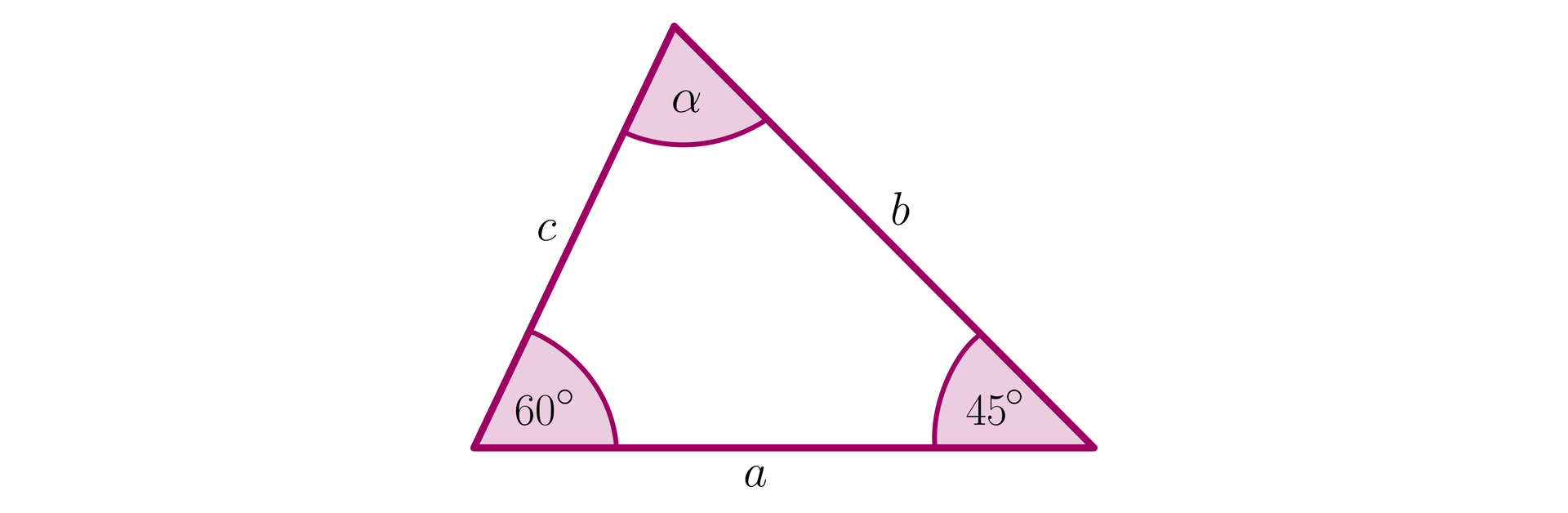
Ilustracja przedstawia trójkąt. Boki trójkąta podpisano literami a b oraz c. Kąt pomiędzy bokami a i c wynosi sześćdziesiąt stopni. Kąt pomiędzy a i b wynosi czterdzieści pięć stopni. Kąt pomiędzy b i c podpisano literą alfa.

Z warunków zadania wynika, że $α = 180 ° - (60 ° + 45 °) = 75 °$ , zatem $a = 12$ .

Do wyznaczenia pola trójkąta użyjemy wzoru $P = \frac{1}{2} a^{2} \cdot \frac{\sin β \cdot \sin γ}{\sin α}$ .

W celu wyznaczenia wielkości $\sin 75 °$ użyjemy wzoru na sinus sumy kątów.

Zatem

$\sin 75 ° = \sin (30 ° + 45 °) = \sin 30 ° \cdot \cos 45 ° + \sin 45 ° \cdot \cos 30 ° =$

$= \frac{1}{2} \cdot \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{2}}{4} + \frac{\sqrt{6}}{4} = \frac{\sqrt{2} + \sqrt{6}}{4}$

Wobec tego pole trójkąta wynosi:

$P = \frac{1}{2} \cdot 12^{2} \cdot \frac{\sin 60 ° \cdot \sin 45 °}{\sin 75 °}$

$P = \frac{1}{2} \cdot 144 \cdot \frac{\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2}}{\frac{\sqrt{2} + \sqrt{6}}{4}} = 72 \cdot \frac{\sqrt{6}}{\sqrt{2} + \sqrt{6}} = 72 \cdot \frac{\sqrt{3}}{1 + \sqrt{3}}$

$P = 108 - 36 \sqrt{3}$

Przykład 5

Kąt przy podstawie trapezu ma miarę $30 °$ , dłuższa podstawa jest równa $12 \sqrt{3}$ , a ramię trapezu ma długość $6$ . Obliczymy długość promienia okręgu opisanego na tym trapezie.

Rozwiązanie:

Wiadomo, że okrąg można opisać na trapezie równoramiennym.

Narysujmy okrąg opisany na trapezie i wprowadźmy oznaczenia, jak na rysunku.

RuQAYyrEI5FA1

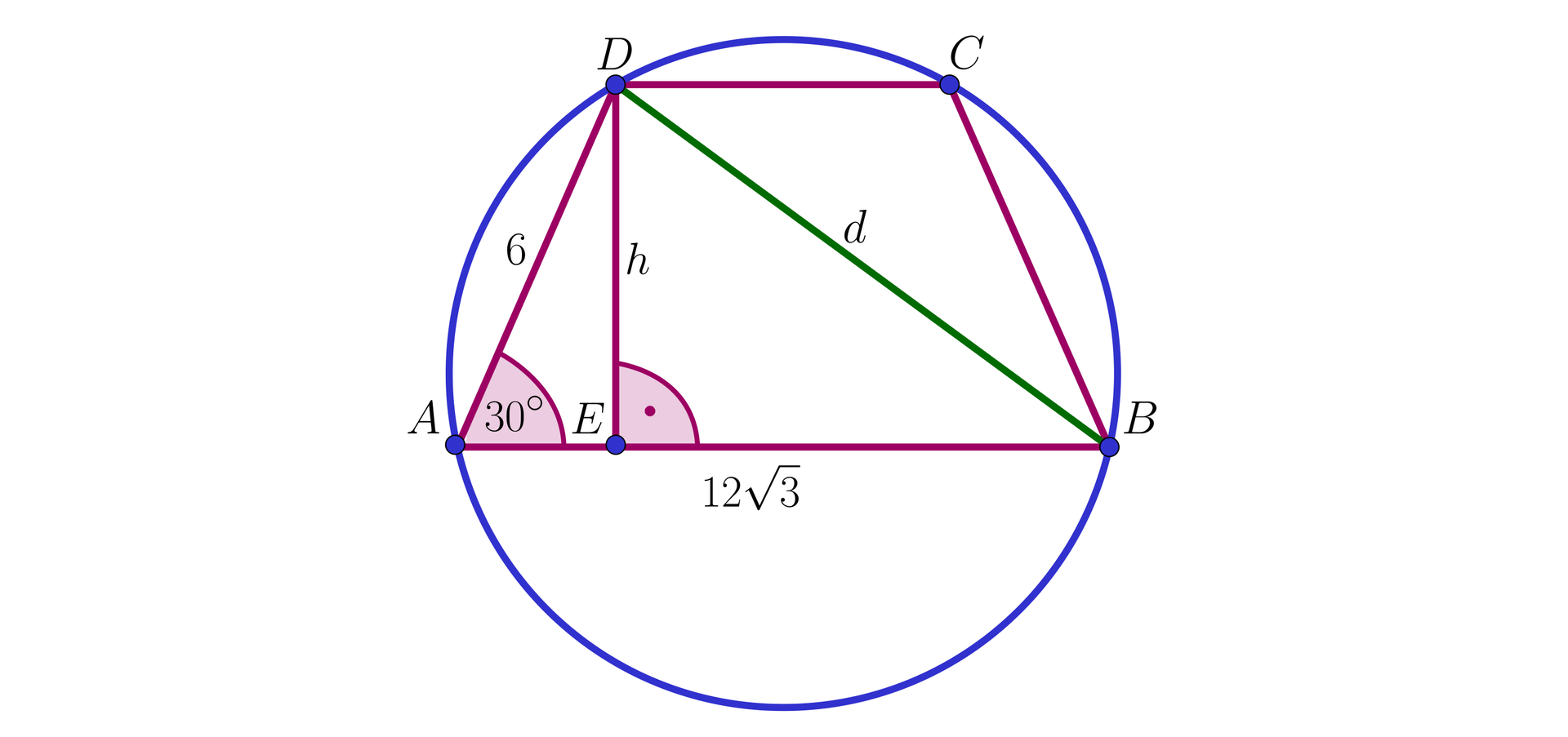
Ilustracja przedstawia trapez równoramienny A B C D wpisany w okrąg. Z wierzchołka D upuszczono wysokość trapezu D E o długości h. Powstał trójkąt prostokątny A E D z podpisanym kątem trzydziestu stopni przy wierzchołku A oraz odcinkiem A D o długości sześć. Na rysunku zaznaczono przekątna trapezu B D o długości d oraz odcinek A B o długości dwanaście pierwiastków z trzech.

Zauważmy, że długość promienia okręgu opisanego na trapezie $A B C D$ jest taka sama, jak długość promienia okręgu opisanego na trójkącie $A B D$ .

Z trójkąta o kątach $90 °$ , $60 °$ , $30 °$ mamy $h = 3$ oraz $|A E| = 3 \sqrt{3}$ .

Zatem $|E B| = 12 \sqrt{3} - 3 \sqrt{3} = 9 \sqrt{3}$ .

Z twierdzenia Pitagorasa mamy:

${(9 \sqrt{3})}^{2} + h^{2} = d^{2}$

${(9 \sqrt{3})}^{2} + 3^{2} = d^{2}$

$243 + 9 = d^{2}$ , czyli $d = \sqrt{252} = 6 \sqrt{7}$

Niech $R$ będzie długością promienia okręgu opisanego na tym trapezie.

Pole trójkąta $A B D$ obliczamy za pomocą wzorów:

$P = \frac{1}{2} \cdot |A B| \cdot |E D|$

$P = \frac{|A B| \cdot |A D| \cdot |B D|}{4 \cdot R}$

Zatem do wyznaczenia wartości $R$ rozwiazujemy równanie:

$\frac{1}{2} \cdot 12 \sqrt{3} \cdot 3 = \frac{12 \sqrt{3} \cdot 6 \cdot 6 \sqrt{7}}{4 \cdot R}$

Wobec tego $R = 6 \sqrt{7}$ .

Słownik

pole trójkąta

miara przyporządkowująca trójkątowi pewną liczbę, która charakteryzuje jej rozmiar

twierdzenie sinusów

w dowolnym trójkącie stosunek długości dowolnego boku do sinusa kąta leżącego naprzeciw tego boku jest stały i równy długości średnicy okręgu opisanego na tym trójkącie

Wprowadzenie

Animacja

Jak zastosować twierdzenie sinusów do obliczania pola trójkąta?

Słownik