Przeczytaj
Graniastosłup prawidłowy trójkątny to taki graniastosłup prostygraniastosłup prosty, który ma w podstawie trójkąt równoboczny.
Bryła ta ma pięć ścian: dwie podstawy i trzy ściany boczne. Poniżej prezentujemy tabelę systematyzującą rodzaje odcinków leżących w płaszczyznach tych ścian oraz podającą ich liczbę i długość w zależności od długości krawędzi podstawy oraz krawędzi bocznej . Odcinki te zostały zaznaczone w przedstawionym niżej aplecie.
Nazwa odcinka | Oznaczenie | Liczba odcinków w graniastosłupie | Wzór na długość odcinka |
|---|---|---|---|
Krawędź podstawy | - | ||
Krawędź boczna | - | ||
Wysokość podstawy | |||
Przekątna ściany bocznej |
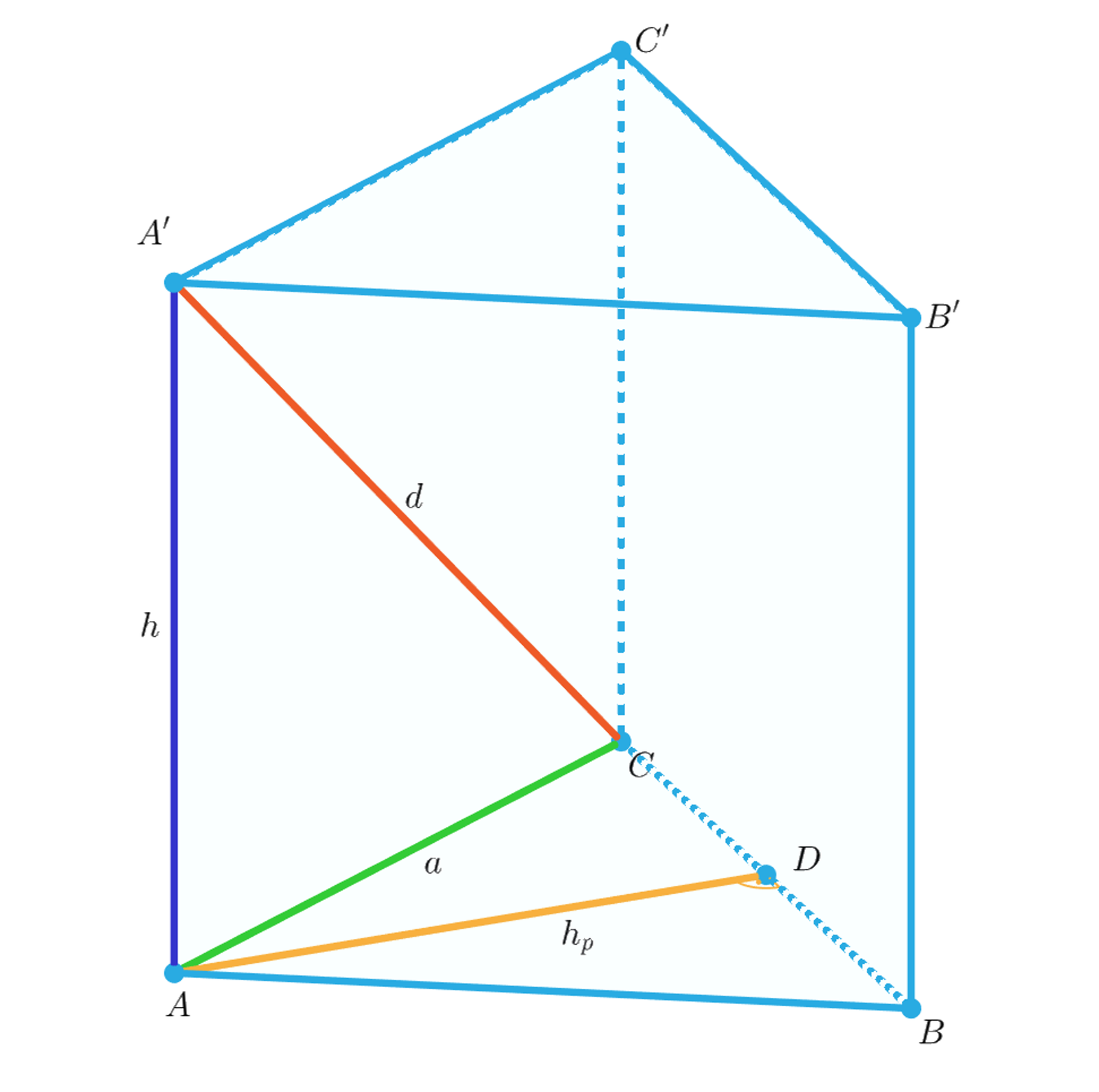
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUsectF8p
Pomiędzy przecinającymi się odcinkami w graniastosłupie powstają różne kąty. Miara części z nich jest stała, innych jest zależna od wymiarów graniastosłupa.
Kąt pomiędzy dwoma krawędziami w podstawie ma miarę , ponieważ figura w podstawie to trójkąt równoboczny.
Kąt pomiędzy krawędzią boczną a dowolnym odcinkiem leżącym w płaszczyźnie podstawy (w tym krawędzią podstawy czy jej wysokością) ma miarę , ponieważ w graniastosłupie prostym każda krawędź boczna jest prostopadła do płaszczyzny podstawy.
Poniżej zajmiemy się więc bardziej skomplikowanymi przypadkami kątów pomiędzy odcinkami w graniastosłupie prawidłowym trójkątnym.
Kąt pomiędzy przekątną ściany bocznej a krawędzią podstawy leżącą na tej samej ścianie
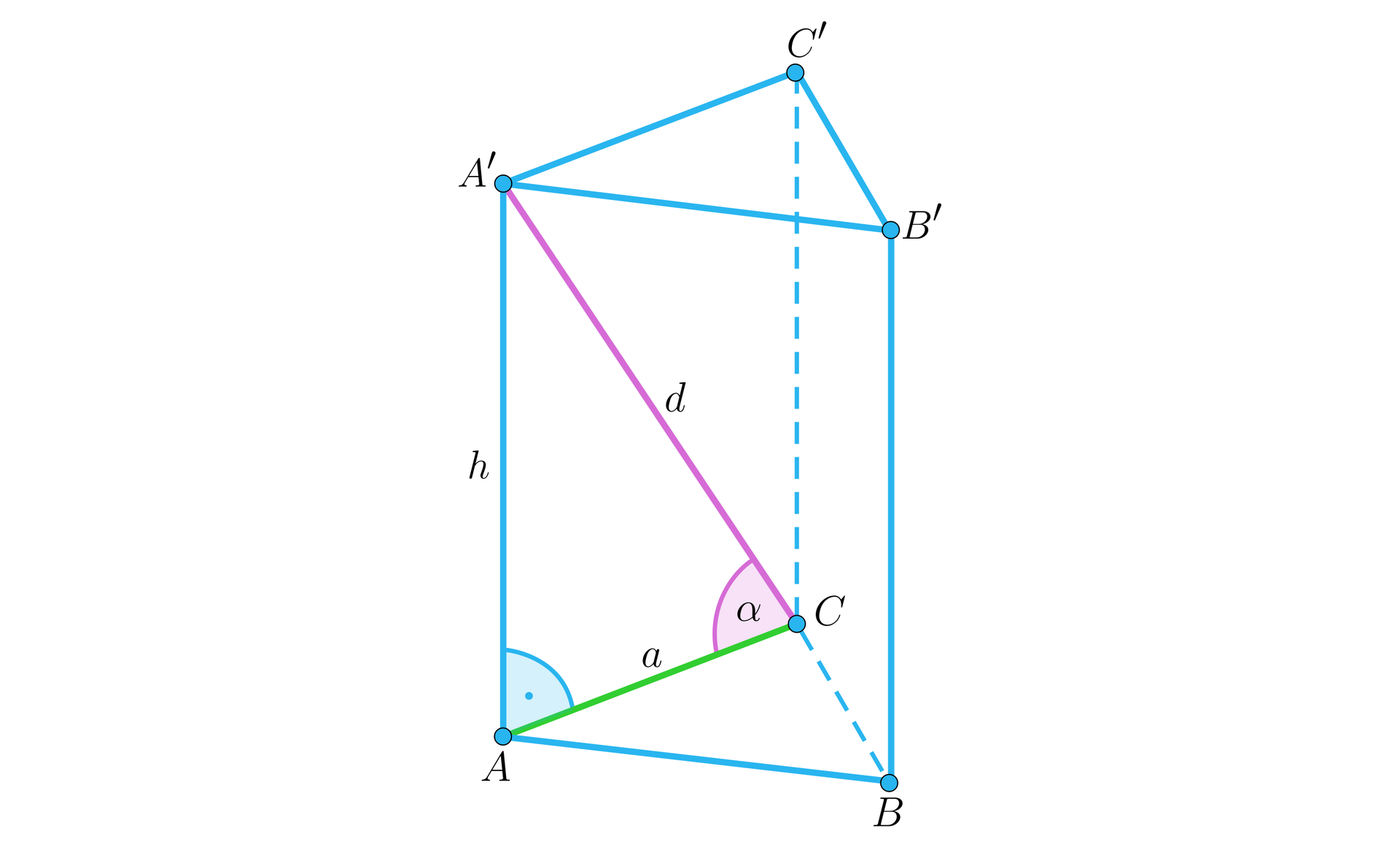
Kąt ten można znaleźć w trójkącie prostokątnym i wyznaczyć z wartości jednej z funkcji trygonometrycznych:
Wyznaczymy miarę kąta pomiędzy przekątną ściany bocznej graniastosłupa prawidłowego trójkątnego a krawędzią podstawy leżącą na tej samej ścianie wiedząc, że obwód podstawy wynosi , a obwód ściany bocznej jest równy .
Rozwiązanie
Obwód podstawy wynosi , zatem .
Obwód ściany bocznej wynosi , zatem , stąd .
Obliczamy tangens szukanego kąta
.
Szukamy odpowiedniej wartości w tablicy wartości funkcji trygonometrycznych.
i podajemy odpowiedź: .
Kąt pomiędzy przekątną ściany bocznej a krawędzią boczną

Kąt ten można znaleźć w trójkącie prostokątnym i wyznaczyć z wartości jednej z funkcji trygonometrycznych:
Warto zauważyć, że suma miar kątów pomiędzy przekątną ściany bocznej a krawędziami odpowiednio podstawy i boczną wynosi :
W graniastosłupie prawidłowym trójkątnym kąt pomiędzy przekątną ściany bocznej a krawędzią boczną ma miarę . Przekątna ściany bocznej jest o dłuższa od krawędzi podstawy. Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.
Rozwiązanie
Suma długości wszystkich krawędzi tego graniastosłupa wynosi .
Kąt pomiędzy przekątną ściany bocznej a wysokością podstawy

Kąt pomiędzy przekątną ściany bocznej a wysokością podstawy można znaleźć w trójkącie . Trójkąt ten jest prostokątny, ponieważ wysokość jest prostopadła do ściany , a więc jest prostopadła do każdej prostej leżącej w płaszczyźnie ściany, w tym do .
Warto zauważyć, że korzystając z twierdzenia Pitagorasatwierdzenia Pitagorasa możemy wyznaczyć długość odcinka w zależności od długości krawędzi graniastosłupa
Dane są następujące wartości funkcji trygonometrycznych omawianego kąta:
Wyznaczymy miarę kąta pomiędzy przekątną ściany bocznej a wysokością podstawy graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy jest razy krótsza od krawędzi bocznej.
Rozwiązanie
Oznaczmy przez długość krawędzi podstawy. Wtedy długość krawędzi bocznej .
Wysokość w podstawie ma długość .
Długość przekątnej ściany bocznej .
Obliczamy cosinus szukanego kąta:
i odczytujemy jego przybliżoną miarę
Kąt pomiędzy przekątnymi ścian bocznych o wspólnym wierzchołku
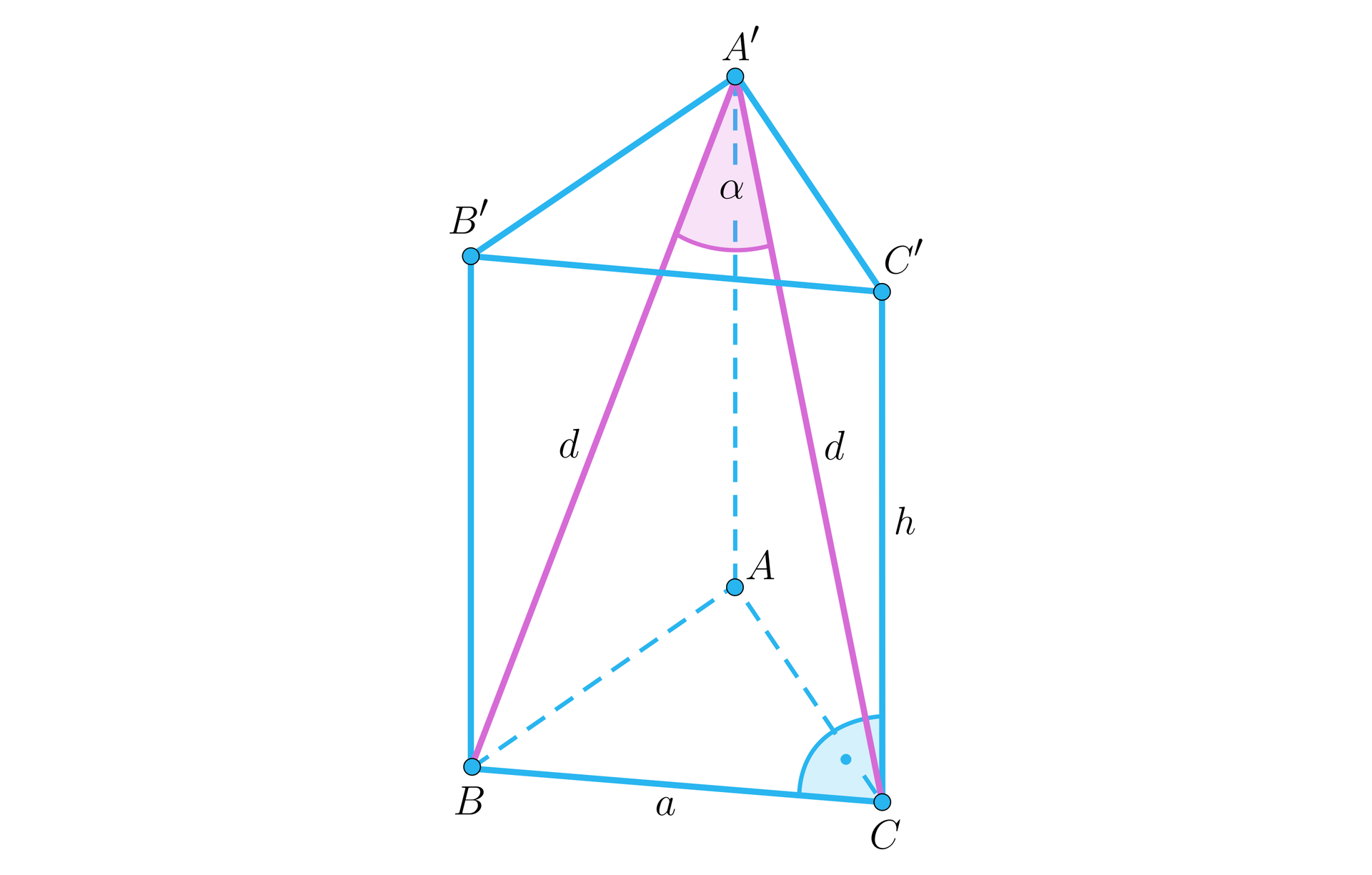
Kąt pomiędzy przekątnymi ścian bocznych o wspólnym wierzchołku leży w trójkącie równoramiennym pomiędzy ramionami o długości , na przeciwko podstawy . Cosinus tego kąta możemy wyznaczyć powołując się na twierdzenie cosinusówtwierdzenie cosinusów:
Z powyższych wyliczeń wynika, że , ponieważ powstaje jako różnica liczby i liczby dodatniej.
Co więcej, z geometrii graniastosłupa prawidłowego trójkątnego wynika, że krawędź podstawy jest krótsza od przekątnej ściany bocznej (ponieważ, przekątna jest przeciwprostokątną w trójkącie o przyprostokątnej ). Zatem możemy oszacować .
Uwzględniając szacowanie w wyznaczonym wzorze na cosinus otrzymujemy informację, że ponieważ cosinus obliczymy jako różnicę liczby i liczby mniejszej niż .
Pamiętając o tym, że dla kątów ostrych funkcja cosinus jest malejąca wnioskujemy, że kąt ma miarę mniejszą niż .
Obliczymy długość krawędzi podstawy graniastosłupa prawidłowego trójkątnego, w którym długość krawędzi bocznej wynosi , a miara kąta pomiędzy przekątnymi ścian bocznych o wspólnym wierzchołku jest jest równa , przy czym .
Rozwiązanie

Korzystając z tw. cosinusów w trójkącie zapisujemy:
uwzględniając fakt, że oraz otrzymujemy
Zapisujemy tw. Pitagorasa w trójkącie prostokątnym :
.
Szukana wielkość .
Kąt pomiędzy przekątną ściany bocznej a krawędzią podstawy leżącą na sąsiedniej ścianie bocznej
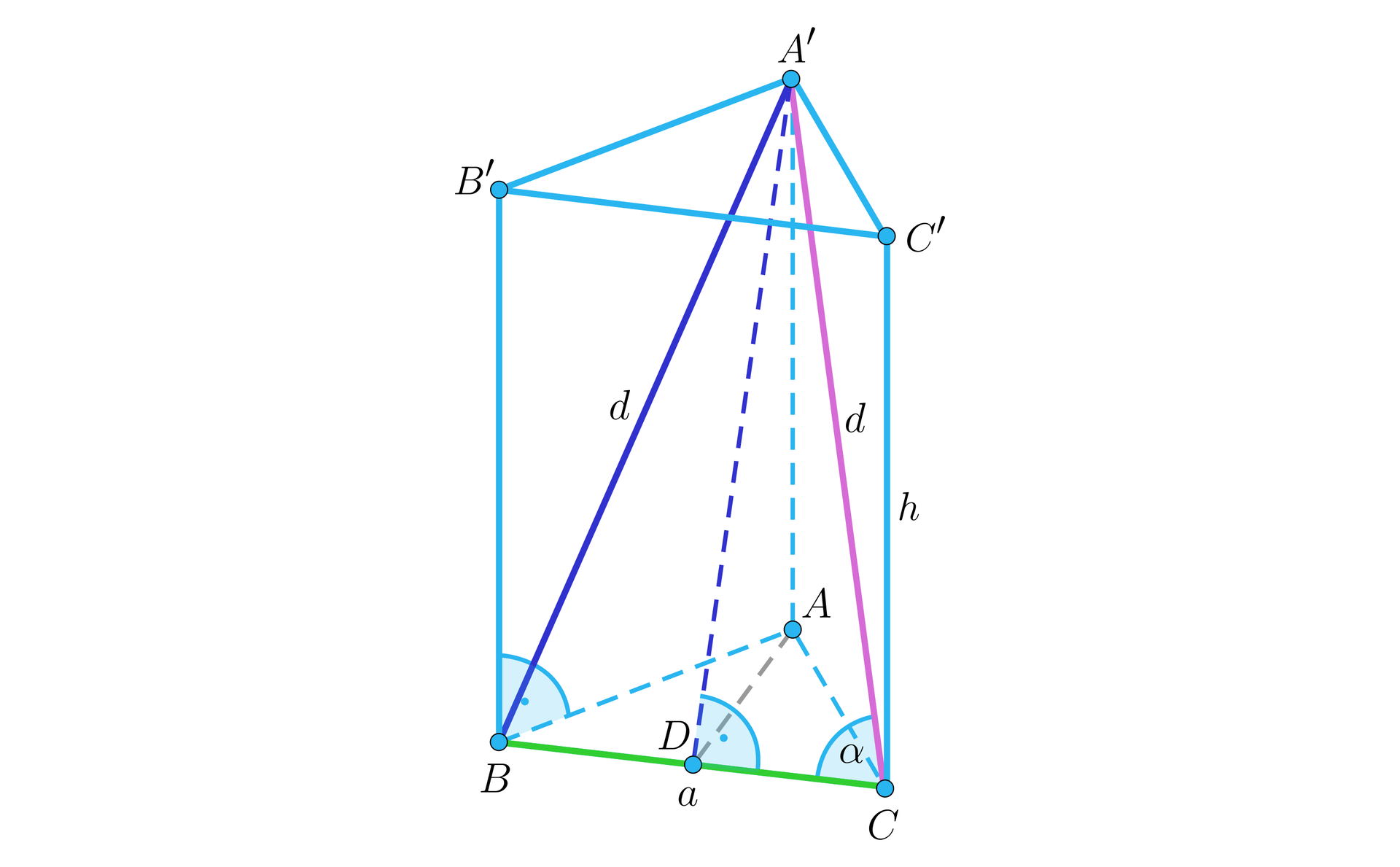
Z jednej strony miarę tego kąta możemy wyznaczyć, podobnie jak w poprzednim przypadku, zapisując twierdzenie cosinusów dla trójkąta równoramiennego .
Podobnie jak poprzednio, , zatem , a więc .
Z drugiej strony, kąt występuje w trójkącie prostokątnym , gdzie jest środkiem krawędzi i jednocześnie spodkiem wysokości w postawie. Jego miarę możemy wyznaczyć korzystając z wartości funkcji trygonometrycznych
W graniastosłupie prawidłowym trójkątnym tangens kąta pomiędzy przekątną ściany bocznej, a krawędzią podstawy leżącą na tej samej ścianie jest równy . Wyznaczymy sinus kąta pomiędzy przekątną ściany bocznej, a krawędzią podstawy leżącą na sąsiedniej ścianie bocznej.
Rozwiązanie
Zaznaczmy na rysunku dwa kąty przedstawione w treści zadania.

Wiemy, że , zatem , czyli .
Z tw. Pitagorasa w trójkącie otrzymujemy
Możemy obliczyć cosinus kąta korzystając z definicji funkcji trygonometrycznych w trójkącie :
Wstawiając wartość cosinusa do jedynki trygonometrycznejjedynki trygonometrycznej i pamiętając, że ma miarę mniejszą niż , otrzymujemy:
.
Słownik
to graniastosłup, w którym wszystkie krawędzie boczne są prostopadłe do podstaw, a więc wszystkie ściany boczne są prostokątami
jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej
w dowolnym trójkącie kwadrat długości dowolnego boku jest równy sumie kwadratów długości dwóch pozostałych boków pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi.
to tożsamość trygonometryczna mówiąca, że suma kwadratów sinusa i cosinusa tego samego kąta jest zawsze równa .
Dla dowolnego kąta zachodzi: