Na podstawie wykresu funkcji $y=a{x}^2+bx+c$ ustalimy znaki liczb: $a$, $b$, $c$, $\Delta$, $p$, $q$, $x_1$, $x_2$, gdzie $p$ jest argumentem, w którym funkcja przyjmuje wartość największą równą  $q$, natomiast $x_1$, $x_2$ to miejsca zerowe funkcji.

RGCGM7Hz5K5D2

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 2 do 5 i pionową osią y od minus 4 do jeden. W układzie zaznaczono wykres funkcji o równaniu $y=a{x}^2+bx+c$, wykres ma kształt paraboli o ramionach skierowanych do dołu. Wierzchołek tej paraboli ma współrzędne nawias dwa średnik jeden zamknięcie nawiasu. Lewe ramię przecina oś y w punkcie nawias zero średnik minus jeden zamknięcie nawiasu.

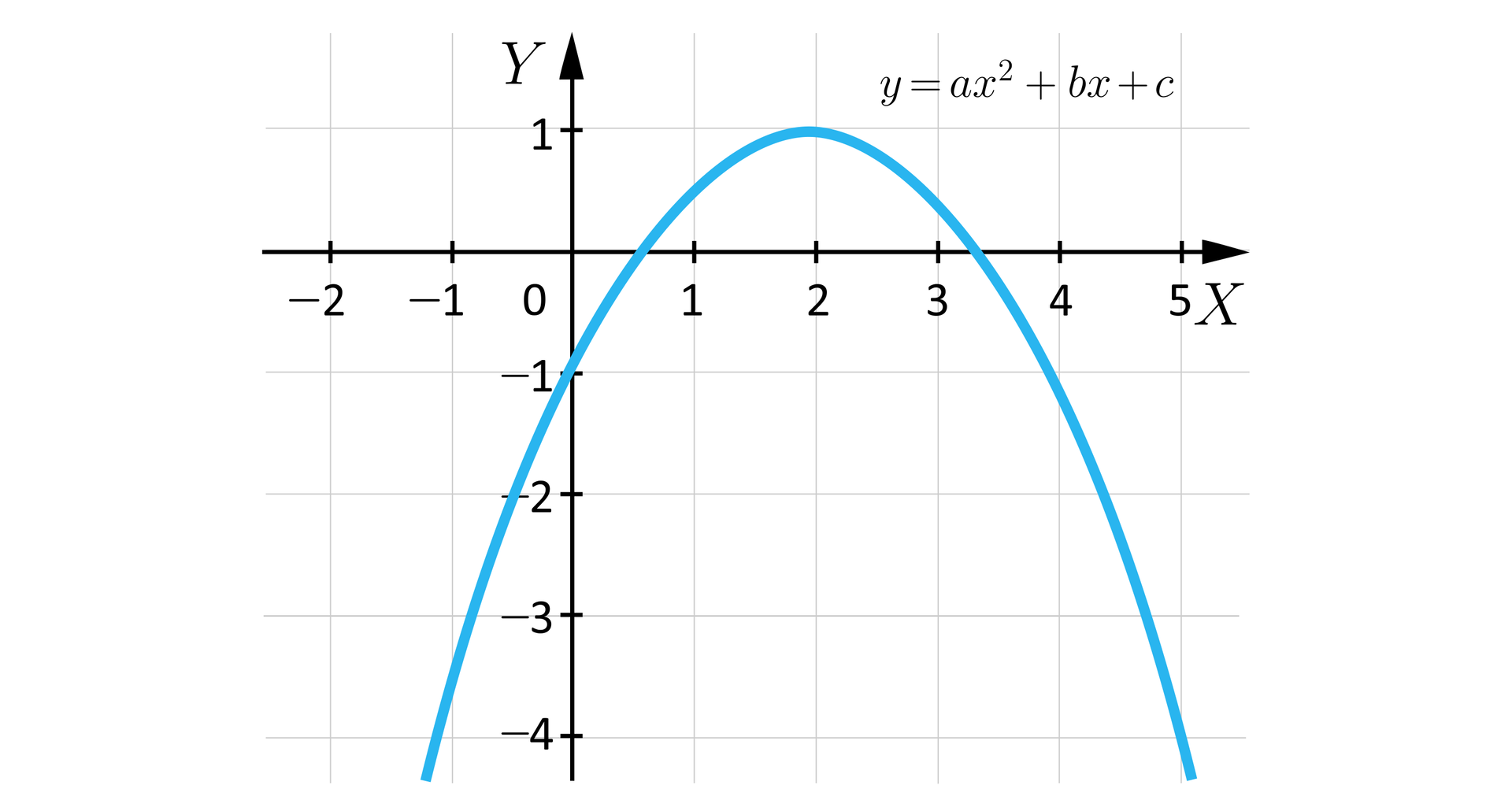
Rozwiązanie

Z wykresu odczytujemy:

• ramiona paraboli skierowane są w dół, co oznacza, że $a<0$;

• funkcja ma dwa miejsca zerowe, więc $\Delta >0$;

• punkt, w którym przyjmowana jest wartość największa funkcji, leży w I ćwiartce układu współrzędnych: $p>0$ i $q>0$;

• wykres przecina oś $Y$ pod osią $X$, czyli: $c<0$,
  $f\left(0\right)=a·0^2+b·0+c=c$: punkt $\left(0;c\right)$ jest punktem przecięcia z osią $Y$;

• wykres funkcji przecina oś $X$ w części dodatniej, stąd: $x_1>0$ i $x_2>0$;

• ponieważ $b=-2ap$ oraz $a<0$ i $p>0$, więc $b>0$.

Na podstawie wykresu funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$:

R1aHEaaftkw68

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 8 do 12 i pionową osią y od minus 6 do sześć. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do góry. Wierzchołek tej paraboli znajduje się w czwartej ćwiartce układu. Lewe ramię paraboli przechodzi przez punkt A o współrzędnych nawias zero średnik minus cztery zamknięcie nawiasu i punkt B o współrzędnych nawias minus cztery średnik zero zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt C o współrzędnych nawias osiem średnik zero zamknięcie nawiasu.

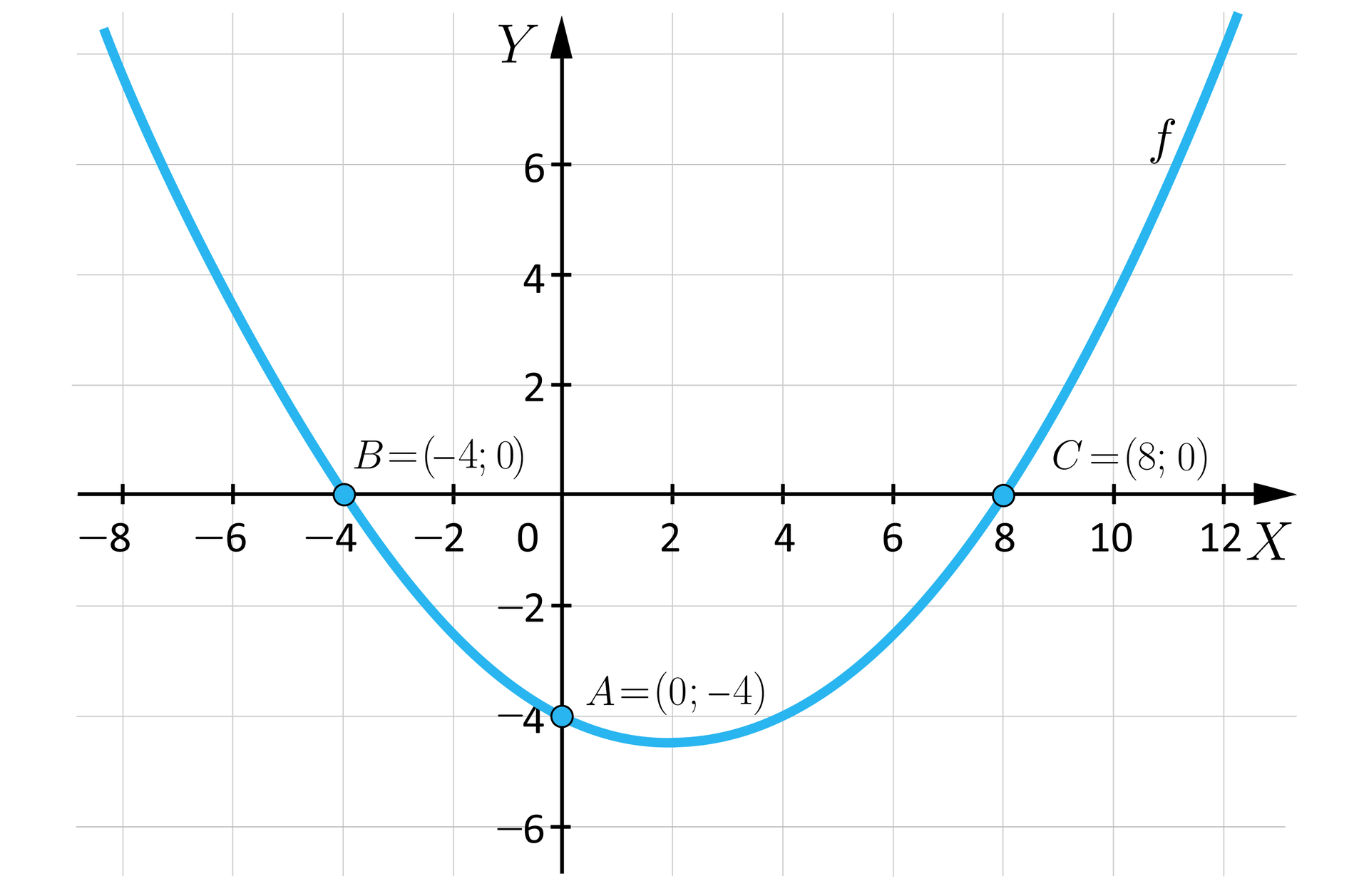
określimy współrzędne wierzchołka i postać kanoniczną; równanie osi symetrii; zbiór wartości funkcji; miejsca zerowe funkcji i postać iloczynową; przedziały monotoniczności; przedziały, w których funkcja przyjmuje wartości większe od $0$; zbiór wartości, jakie przyjmuje funkcja w przedziale $⟨-2;10⟩$; najmniejszą i największą wartość funkcji w tym przedziale.

Rozwiązanie

Na wykresie zaznaczamy oś symetrii paraboli oraz zaznaczamy przedziały, w których funkcja przyjmuje wartości dodatnie.

RIK4DTIRMOrng

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 8 do 12 i pionową osią y od minus 6 do sześć. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do góry. Wierzchołek tej paraboli znajduje się w czwartej ćwiartce układu. Lewe ramię paraboli przechodzi przez punkt A o współrzędnych nawias zero średnik minus cztery zamknięcie nawiasu i punkt B o współrzędnych nawias minus cztery średnik zero zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt C o współrzędnych nawias osiem średnik zero zamknięcie nawiasu. W układzie za pomocą linii przerywanej zaznaczono również pionową prostą o równaniu $x=2$. Wierzchołek paraboli leży na tej prostej. Na osi x zaznaczono obszary od minus nieskończoności do minus czterech oraz od ośmiu do plus nieskończoności.

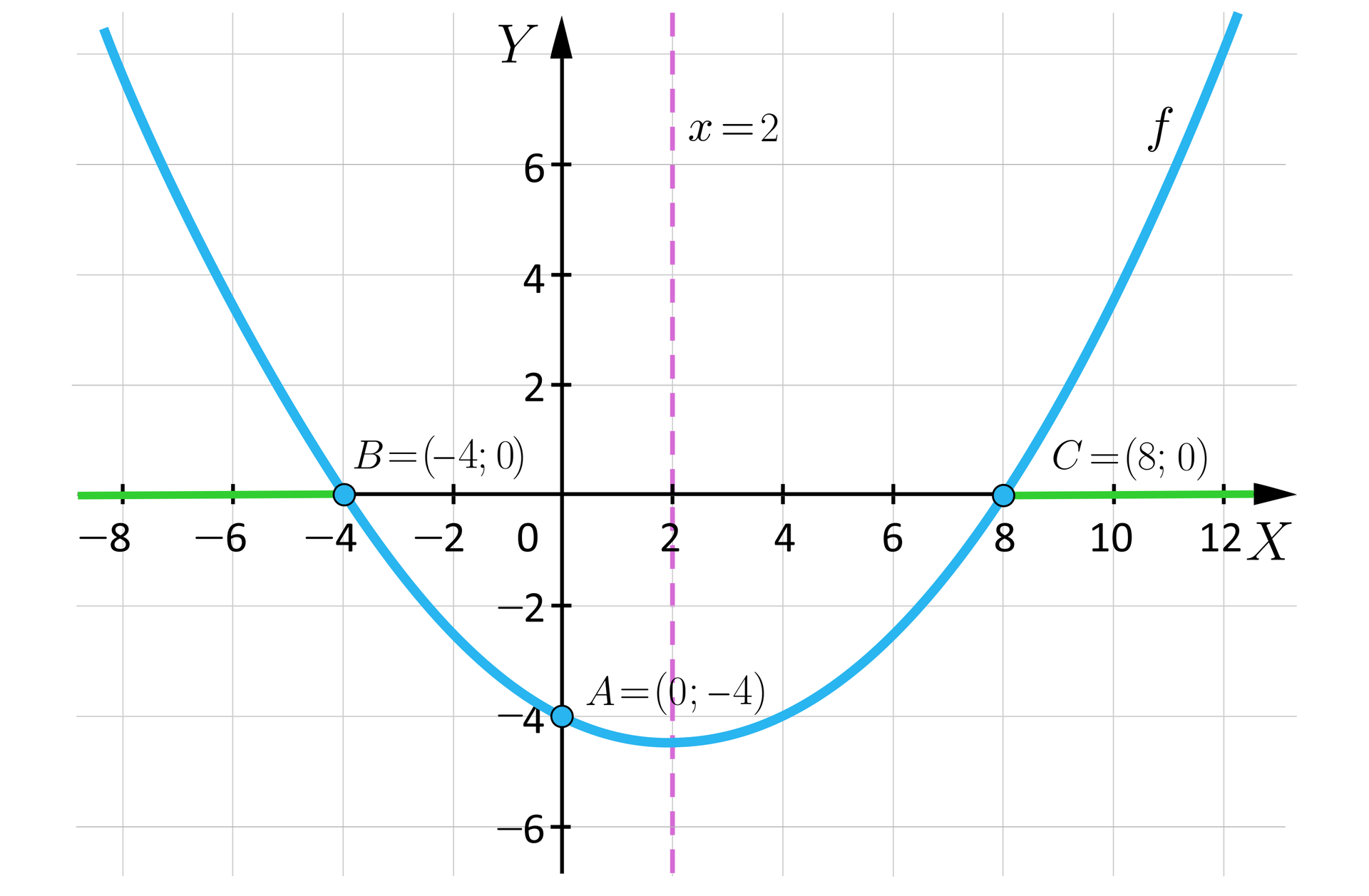
Z wykresu możemy odczytać:

• miejsca zerowe funkcji: $x_1=-4$ i $x_2=8$;

• oś symetrii paraboli: $x=2$ (ponieważ przechodzi przez środek odcinka $BC$);

• pierwszą współrzędną wierzchołka $p=2$ (ponieważ leży na osi symetrii paraboli);

• przedziały, w których funkcja przyjmuje wartości dodatnie: $f\left(x\right)>0$ dla $x\in \left(-\infty ;-4\right)\cup \left(8;+\infty \right)$;

• przedział, w którym funkcja jest malejąca: $x\in \left(-\infty ;2\right)$;

• przedział, w którym funkcja jest rosnąca: $x\in \left(2;+\infty \right)$.

Odpowiedzi do pozostałych poleceń określimy po podaniu wzoru funkcji, której wykres jest przedstawiony na rysunku.

Zapisujemy wzór funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej w postaci iloczynowej:

$f\left(x\right)=a\left(x-x_1\right)\left(x-x_2\right)$.

Miejsca zerowe to: $x_1=-4$ i $x_2=8$, więc wzór  funkcji możemy zapisać następująco:

$f\left(x\right)=a\left(x+4\right)\left(x-8\right)$.

Podstawiając współrzędne punktu $A =\left(0;-4\right)$ do wzoru funkcji $f\left(x\right)=a\left(x+4\right)\left(x-8\right)$, otrzymujemy:

$f\left(0\right)=a·\left(0+4\right)·\left(0-8\right)=-32a$,

a ponieważ

$f\left(0\right)=-4$, czyli

$a=\frac{1}{8}$.

Funkcja, której wykres przedstawiony jest na rysunku, ma postać:

$f\left(x\right)=\frac{1}{8}\left(x+4\right)\left(x-8\right)$.

Zapisujemy teraz wzór tej funkcji w postaci kanonicznej:

$f\left(x\right)=a{\left(x-p\right)}^2+q$.

Ponieważ $p=2$, więc $q=f\left(p\right)$, czyli

$q=f\left(2\right)=\frac{1}{8}·\left(2+4\right)·\left(2-8\right)=\frac{1}{8}·\left(6\right)·\left(-6\right)=-\frac{36}{8}=-\frac{9}{2}$.

Wartość najmniejsza  $q=-\frac{9}{2}$ osiągana jest dla argumentu $p=2$.

Wzór funkcji w postaci kanonicznej zapisujemy następująco:

$f\left(x\right)=\frac{1}{8}{\left(x-2\right)}^2-\frac{9}{2}$.

A ponieważ $a>0$, to $Z{W}_f=\left.⟨q;+\infty \right)$, więc $Z{W}_f=\left.⟨\frac{-9}{2};+\infty \right)$.

Z wykresu wynika, że funkcja w przedziale $⟨-2;10⟩$ przyjmuje wartości od $f\left(p\right)$ do $f\left(10\right)$.

Wyliczamy wartość funkcji dla $x=10$:

$f\left(10\right)=\frac{1}{8}·\left(10+4\right)·\left(10-8\right)=\frac{1}{8}·\left(14\right)·\left(2\right)=\frac{28}{8}=\frac{7}{2}$.

Rs4sGXCkoHtkK

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 8 do 12 i pionową osią y od minus 6 do sześć. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do góry. Wierzchołek tej paraboli znajduje się w czwartej ćwiartce układu. Lewe ramię paraboli przechodzi przez punkt A o współrzędnych nawias zero średnik minus cztery zamknięcie nawiasu i punkt B o współrzędnych nawias minus cztery średnik zero zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt C o współrzędnych nawias osiem średnik zero zamknięcie nawiasu. Na osi x zaznaczono obszar od minus dwóch do dziesięciu, przy czym końce tego obszaru połączono z wykresem funkcji f. Za pomocą klamry zaznaczono wartości od wierzchołka paraboli do wartości funkcji odpowiadającej wartości x równej dziesięć. Klamrę podpisano literą y.

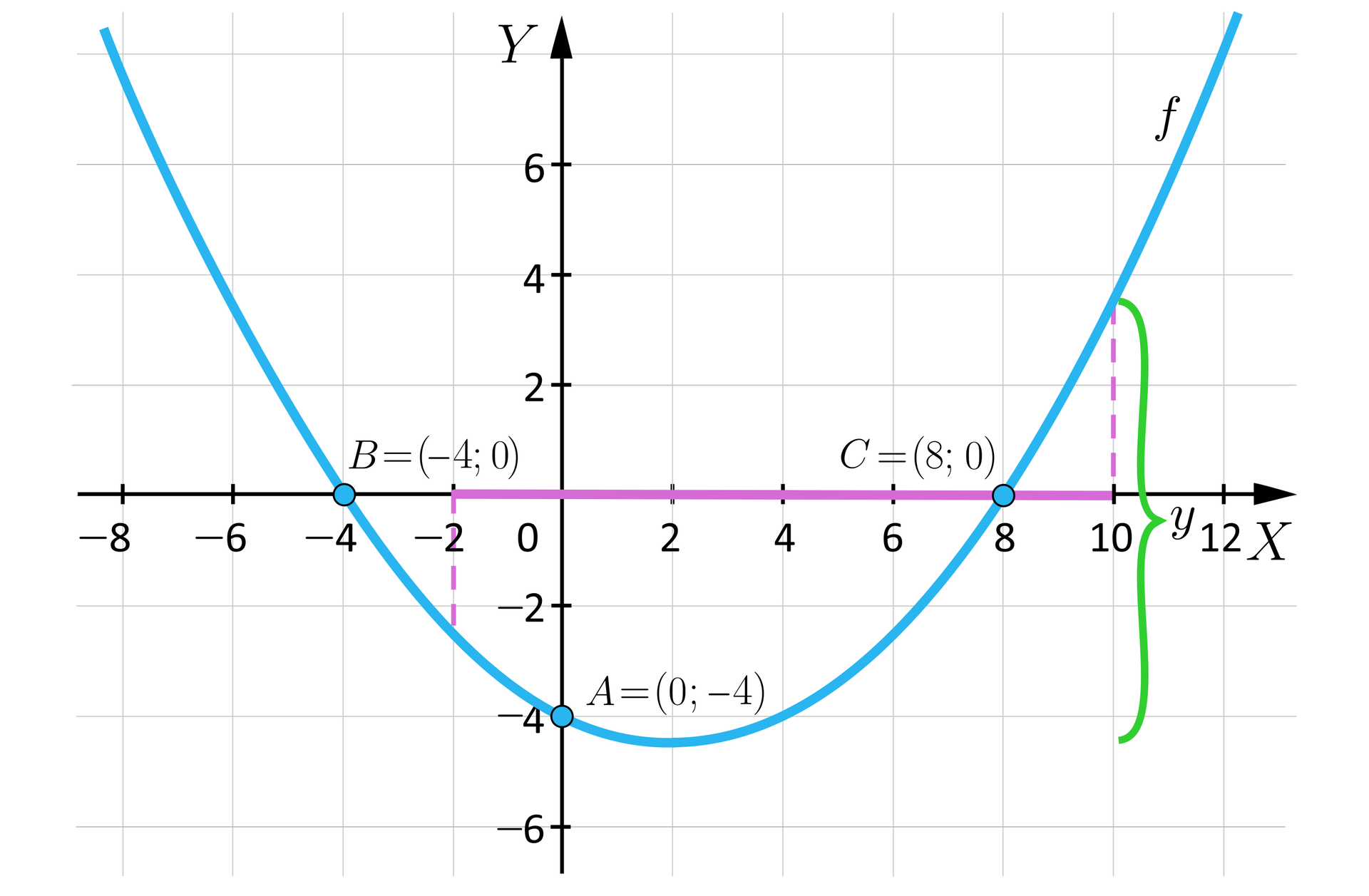
Widzimy, że funkcja przyjmuje w tym przedziale wartości: $y\in ⟨\frac{-9}{2};\frac{7}{2}⟩$.

Najmniejszą wartość w przedziale $⟨-2;10⟩$ funkcja przyjmuje dla $x=2$: $y_{\min }=-\frac{9}{2}$, największą dla $x=10$: $y_{\max }=\frac{7}{2}$.

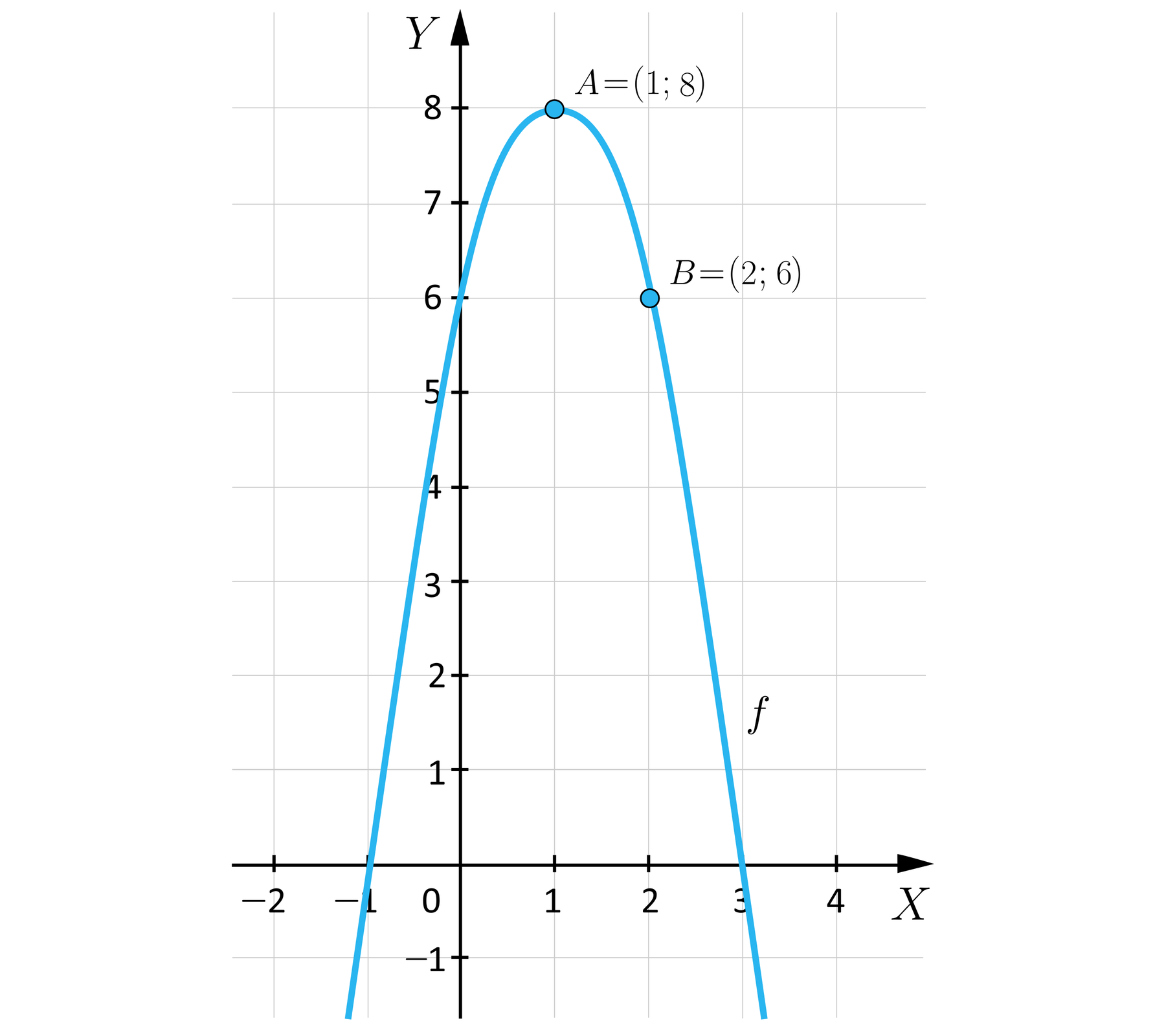
Na podstawie wykresu określimy: współrzędne wierzchołka, oś symetrii paraboli, zbiór wartości funkcji, przedziały monotoniczności, miejsca zerowe, przedział, w którym funkcja przyjmuje wartości nie mniejsze od $6$.

Rxa0huONBUO69

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 2 do 4 i pionową osią y od minus 1 do osiem. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do dołu. Wierzchołek tej paraboli znajduje się w punkcie A o współrzędnych nawias jeden średnik osiem zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt B o współrzędnych nawias dwa średnik sześć zamknięcie nawiasu.

Rozwiązanie

Z wykresu odczytujemy:

• punkt $A$ jest wierzchołkiem paraboli, współrzędne wierzchołka: $p=1$, $q=8$;

• oś symetrii paraboli: $x=1$ (ponieważ wierzchołek leży na osi paraboli);

• zbiór wartości funkcji $Z{W}_f=\left(-\infty ;8\right.⟩$;

• przedziały monotoniczności: funkcja jest rosnąca w przedziale $x\in \left(-\infty ;1\right)$, a malejąca w przedziale $x\in \left(1;+\infty \right)$.

Miejsca zerowe możemy odczytać z wykresu, ale możemy też wyliczyć je ze wzoru funkcji. W tym celu teraz wyznaczymy  wzór funkcji – ponieważ znamy współrzędne wierzchołka paraboli najlepiej skorzystać z postaci kanonicznej.

Zapiszmy wzór  funkcji  w postaci kanonicznej.

Aby podać miejsca zerowe, musimy podać wzór funkcji. Wykorzystamy w tym celu współrzędne punktu $B=\left(2;6\right)$.

$f\left(x\right)=a{\left(x-p\right)}^2+q$.

Podstawiając $p=1$ i $q=8$, otrzymujemy:

$f\left(x\right)=a{\left(x-1\right)}^2+8$.

Punkt $B=\left(2;6\right)$ leży na paraboli będącej wykresem funkcji $f\left(x\right)=a{\left(x-1\right)}^2+8$, czyli $f\left(2\right)=6$, więc

$f\left(2\right)=a{\left(2-1\right)}^2+8$, czyli

$a+8=6$.

Ostatecznie otrzymujemy: $a=-2$.

Wzór funkcji w postaci kanonicznej jest postaci: $f\left(x\right)=-2{\left(x-1\right)}^2+8$.

Wyliczamy miejsca zerowe, korzystając ze wzorów:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}$ i $x_2=\frac{-b-\sqrt{\Delta }}{2a}$.

Aby wyliczyć $x_1$ i $x_2$, potrzebujemy wartości $b$ i $\Delta$, które możemy wyznaczyć, wykorzystując przekształcone wzory:

$p=-\frac{b}{2a}$ i $q=-\frac{\Delta }{4a}$.

Skoro $p=-\frac{b}{2a}$, to $b=-2ap$, a po podstawieniu $p=1$ i $a=-2$, mamy:

$b=-2·\left(-2\right)·1=4$.

Skoro $q=-\frac{\Delta }{4a}$, to $\Delta =-4aq$, a po podstawieniu $q=8$ i $a=-2$, mamy:

$\Delta =-4·\left(-2\right)·8=64$.

Obliczone wartości $b$ i $\Delta$ podstawiamy do wzorów:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-4+\sqrt{64}}{2\left(-2\right)}=\frac{-4+8}{-4}=-1$,

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-4-\sqrt{64}}{2\left(-2\right)}=\frac{-4-8}{-4}=3$.

Możemy również wyznaczyć $x_1$ i $x_2$, opierając się na wzorze funkcji zapisanej w postaci ogólnej.

Wykorzystując wzór skróconego mnożenia ${\left(m-n\right)}^2=m^2-2mn+n^2$, przechodzimy ze wzoru zapisanego w postaci kanonicznej do postaci ogólnej:

$f\left(x\right)=-2{\left(x-1\right)}^2+8=-2\left(x^2-2x+1\right)+8=$

$=-2x^2+4x-2+8=-2x^2+4x+6$.

Otrzymujemy $b=4$ i $\Delta =b^2-4ac=4^2-4·\left(-2\right)·6=16+48=64$.

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-4+\sqrt{64}}{2\left(-2\right)}=\frac{-4+8}{-4}=-1$,

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-4-\sqrt{64}}{2\left(-2\right)}=\frac{-4-8}{-4}=3$.

Określimy teraz przedział, w którym funkcja przyjmuje wartości nie mniejsze od $6$, czyli $f\left(x\right)\ge 6$.

R8va4ymgcepTJ

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 2 do 4 i pionową osią y od minus 1 do osiem. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do dołu. Wierzchołek tej paraboli znajduje się w punkcie A o współrzędnych nawias jeden średnik osiem zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt B o współrzędnych nawias dwa średnik sześć zamknięcie nawiasu. W układzie zaznaczono również poziomą prostą o współrzędnych $y=6$, przechodzi ona przez punkt B. Z punktu B poprowadzono pionowy odcinek prowadzący do osi x. Na osi x zaznaczono obszar od zero do dwóch.

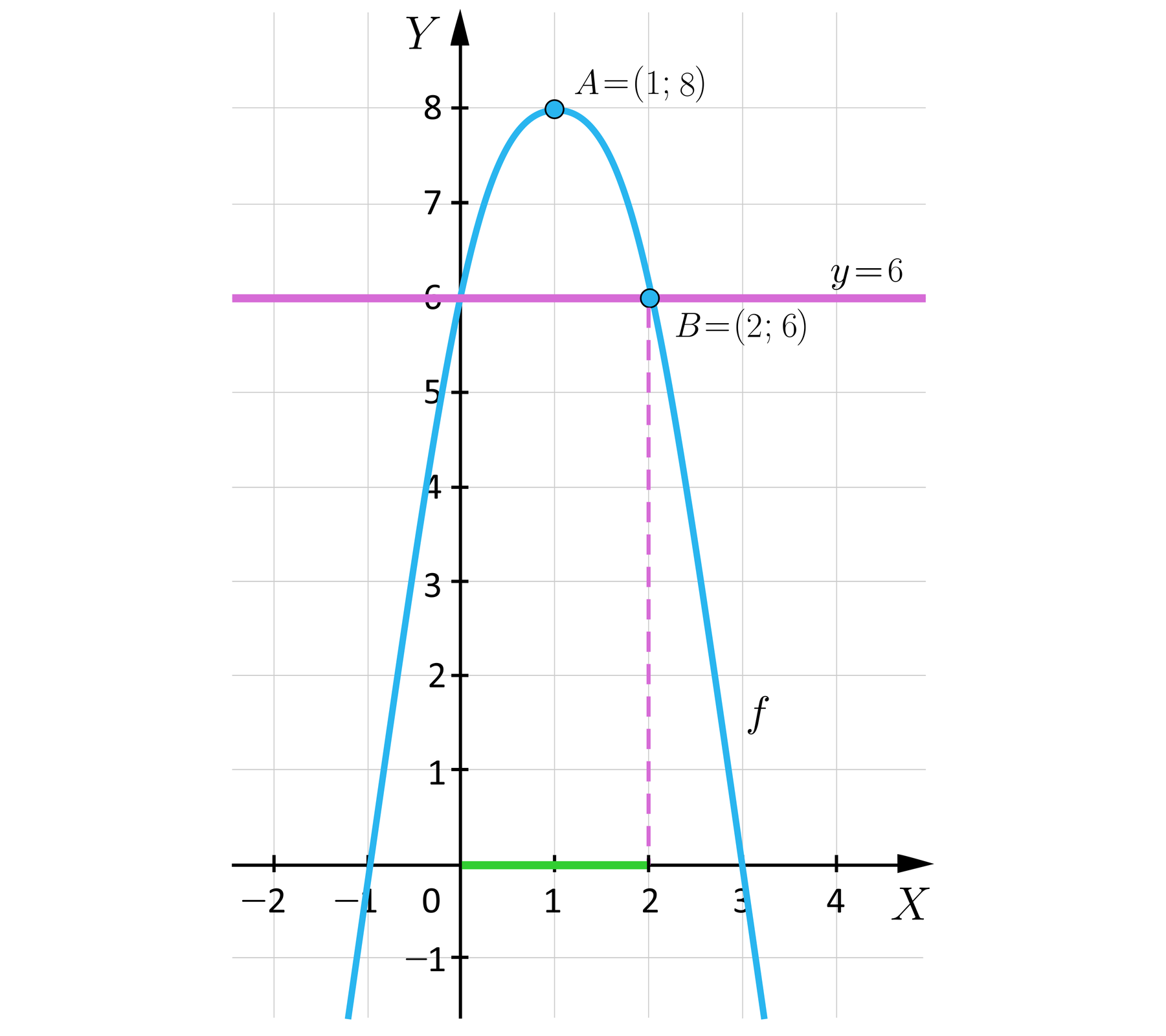
Funkcja przyjmuje wartości nie mniejsze od $6$, $f\left(x\right)⩾6$, gdy $x\in ⟨0;2⟩$.

funkcja $f\left(x\right)=a{x}^2+bx+c$ określona dla wszystkich liczb rzeczywistych, gdzie $a$, $b$, $c$ są liczbami rzeczywistymi, przy czym $a\ne 0$

wykres funkcji $f\left(x\right)=a{x}^2+bx+c$ dla $x\in \mathrm{ℝ}$, gdzie $a\ne 0$ jest krzywa zwana parabolą