Przeczytaj

W materiale omówimy różne własności funkcji liniowej, korzystając z jej wzoru oraz wykresu.

monotoniczność funkcji liniowej

Własność: monotoniczność funkcji liniowej

Funkcja liniowa określona wzorem $f (x) = a x + b$ jest:

rosnąca, gdy $a > 0$ ,
RBNMH1Zh50X0T

malejąca, gdy $a < 0$ ,
RV1cMyUMI7tcM

stała, gdy $a = 0$ .
RTuuQX6pGtIh2

Monotonicznośćmonotoniczność funkcjiMonotoniczność oraz istnienie miejsca zerowegomiejsce zerowe funkcjimiejsca zerowego funkcji liniowej decyduje o tym, w jakim przedziale funkcja przyjmuje wartości ujemne, a w jakim wartości dodatnie.

Niech $x_{0}$ będzie miejscem zerowym funkcji liniowej określonej wzorem
$f (x) = a x + b$ .

Jeżeli $a > 0$ , to:

funkcja przyjmuje wartości ujemne dla $x \in (- \infty, x_{0})$ ,

funkcja przyjmuje wartości dodatnie dla $x \in (x_{0}, \infty)$ .

Jeżeli $a < 0$ , to

funkcja przyjmuje wartości dodatnie dla $x \in (- \infty, x_{0})$ ,

funkcja przyjmuje wartości ujemne dla $x \in (x_{0}, \infty)$ .

Jeżeli $a = 0$ , to:

dla $b > 0$ funkcja przyjmuje tylko wartości dodatnie,

dla $b < 0$ funkcja przyjmuje tylko wartości ujemne.

Punkty szczególne, które należą do wykresu funkcji liniowej:

punkt przecięcia wykresu funkcji z osią $X$ ma współrzędne $(- \frac{b}{a}, 0)$ , dla $a \neq 0$ ,

punkt przecięcia wykresu funkcji z osią $Y$ ma współrzędne $(0, b)$ .

R1PVrvOWuZqt6

Ilustracja przedstawia układ współrzędnych z osią X i Y. Prosta rosnąca przechodzi przez osie tworząc punkty przecięcia w pierwszej drugiej oraz trzeciej ćwiartce.

Przykład 1

Na podstawie wykresu funkcji liniowej, odczytamy:

a) punkty przecięcia wykresu tej funkcji z osiami układu współrzędnych,

b) dla jakich argumentów funkcja przyjmuje wartości ujemne, a dla jakich dodatnie.

RugcxMJ8tdW2n

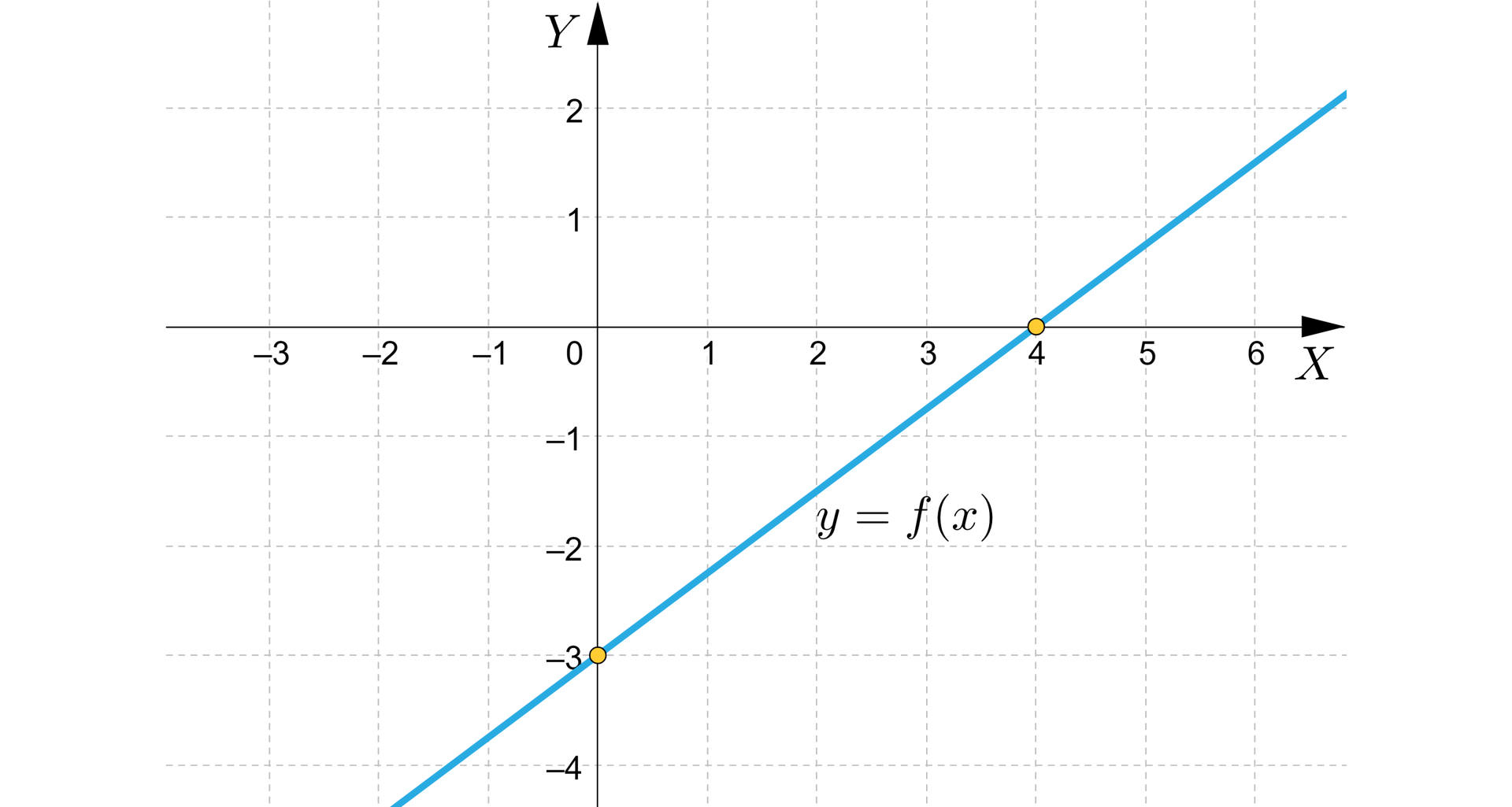
Ilustracja przedstawia układ współrzędnych z poziomą osią od minus 3 do sześciu oraz pionową osią od minus 4 do dwóch. Zaznaczono prostą rosnącą mającą miejsce zerowe równe cztery i wyraz wolny równy minus trzy.

Rozwiązanie

a) Punkt przecięcia wykresu funkcji z osią $X$ : $(4, 0)$ .

Punkt przecięcia wykresu funkcji z osią $Y$ ma współrzędne $(0, - 3)$ .

b) Z wykresu funkcji odczytujemy, że miejscem zerowym jest liczba $4$ .

Zauważmy, że funkcja jest rosnąca, zatem $a > 0$ .

Zatem funkcja przyjmuje wartości:

ujemne dla argumentów $x \in (- \infty, 4)$ ,

dodatnie dla argumentów $x \in (4, \infty)$ .

Wiedząc o tym, od czego zależy monotoniczność funkcji liniowej, możemy wyznaczać wartości parametrów we wzorze funkcji, dla których funkcja rośnie, maleje lub jest stała.

Przykład 2

Określimy, dla jakiej wartości parametru $m$ funkcja liniowa określona wzorem $f (x) = (- \frac{2}{3} m + \frac{1}{2}) x - 3$ jest malejąca.

Rozwiązanie

Ze wzoru funkcji możemy odczytać, że $a = - \frac{2}{3} m + \frac{1}{2}$ .

Jeżeli funkcja jest malejąca, to $a < 0$ , zatem do wyznaczenia wartości parametru $m$ rozwiązujemy nierówność:

$- \frac{2}{3} m + \frac{1}{2} < 0$

Zatem $m \in (\frac{3}{4}, \infty)$ .

Przykład 3

Obliczymy pole figury ograniczonej osiami układu współrzędnych oraz wykresem funkcji liniowej zadanej wzorem $f (x) = - \frac{1}{2} x + \frac{9}{5}$ .

Rozwiazanie

Obliczymy punkty przecięcia wykresu funkcji $f$ z osiami układu współrzędnych.

$0 = - \frac{1}{2} x + \frac{9}{5}$ , zatem $x = \frac{18}{5}$ .

Punkt przecięcia z osią $X$ ma współrzędne $(\frac{18}{5}, 0)$ .

Punkt przecięcia z osią $Y$ ma współrzędne $(0, \frac{9}{5})$ .

Wykres tej funkcji przedstawia się następująco:

RNlS6OsqL4d0A

Ilustracja przedstawia układ współrzędnych z poziomą osią od minus 3 do sześciu oraz pionową osią od minus 1 do trzech. Zaznaczono prostą malejącą przecinającą oś Y w punkcie dziewięć piątych oraz mającą miejsce zerowe równe 18 piątych.

Zauważmy, że figurą ograniczoną prostą, która jest wykresem tej funkcji oraz osiami układu współrzędnych jest trójkąt prostokątny.

Do wyznaczenia pola tego trójkąta użyjemy wzoru $P = \frac{1}{2} \cdot a \cdot h$ .

Z rysunku możemy odczytać, że $a = \frac{18}{5}$ oraz $h = \frac{9}{5}$ .

Zatem $P = \frac{1}{2} \cdot \frac{18}{5} \cdot \frac{9}{5} = \frac{81}{25}$ .

Przykład 4

Do wykresu funkcji liniowej określonej wzorem $f (x) = 3 m x + \frac{3}{4}$ należy punkt o współrzędnych $(- 1, 2)$ . Wyznaczymy, dla jakich argumentów funkcja przyjmuje wartości dodatnie.

Rozwiązanie

Ponieważ punkt o współrzędnych $(- 1, 2)$ należy do wykresu tej funkcji, zatem do wyznaczenia wartości $m$ rozwiązujemy równanie:

$2 = 3 \cdot m \cdot (- 1) + \frac{3}{4}$ , zatem $m = - \frac{5}{12}$

Funkcja jest określona wzorem $f (x) = - \frac{5}{4} x + \frac{3}{4}$ .

Ze wzoru funkcji odczytujemy, że $a = - \frac{5}{4}$ .

Obliczamy miejsce zerowe tej funkcji.

$- \frac{5}{4} x + \frac{3}{4} = 0$ , zatem $x = \frac{3}{5}$

Funkcja przyjmuje wartości dodatnie dla argumentów $x \in (- \infty, \frac{3}{5})$ .

Przykład 5

Określimy monotoniczność funkcji zadanej wzorem $f (x) = (6 - 2 m) x + 2$ w zależności od wartości parametru $m \in ℝ$ .

Rozwiązanie

Ponieważ $a = 6 - 2 m$ , wobec tego:

funkcja jest rosnąca, gdy $6 - 2 m > 0$ , zatem $m \in (- \infty, 3)$ ,

funkcja jest malejąca, gdy $6 - 2 m < 0$ , zatem $m \in (3, \infty)$ ,

funkcja jest stała, gdy $6 - 2 m = 0$ , zatem $m = 3$ .

Przykład 6

Funkcja liniowa jest określona wzorem $f (x) = - 3 x + b - 4$ . Wyznaczymy liczbę $b$ , dla której:

a) miejscem zerowym tej funkcji jest liczba $(- 2)$ ,

b) wykres tej funkcji przecina oś $Y$ w punkcie o rzędnej $1$ .

Rozwiązanie

a) Korzystając ze wzoru na miejsce zerowe funkcji liniowej, rozwiązujemy równanie:

$\frac{- b + 4}{- 3} = - 2$

Zatem $b = - 2$ .

b) Jeżeli wykres funkcji liniowej przecina oś $Y$ w punkcie o rzędnej $1$ , to do wyznaczenia wartości $b$ rozwiązujemy równanie $b - 4 = 1$ .

Zatem $b = 5$ .

Słownik

monotoniczność funkcji

własność funkcji, która określa zmianę wartości tej funkcji wraz ze zmianą argumentów

miejsce zerowe funkcji

argument, dla którego wartość funkcji wynosi $0$

Wprowadzenie

Schemat interaktywny

Słownik