Przeczytaj
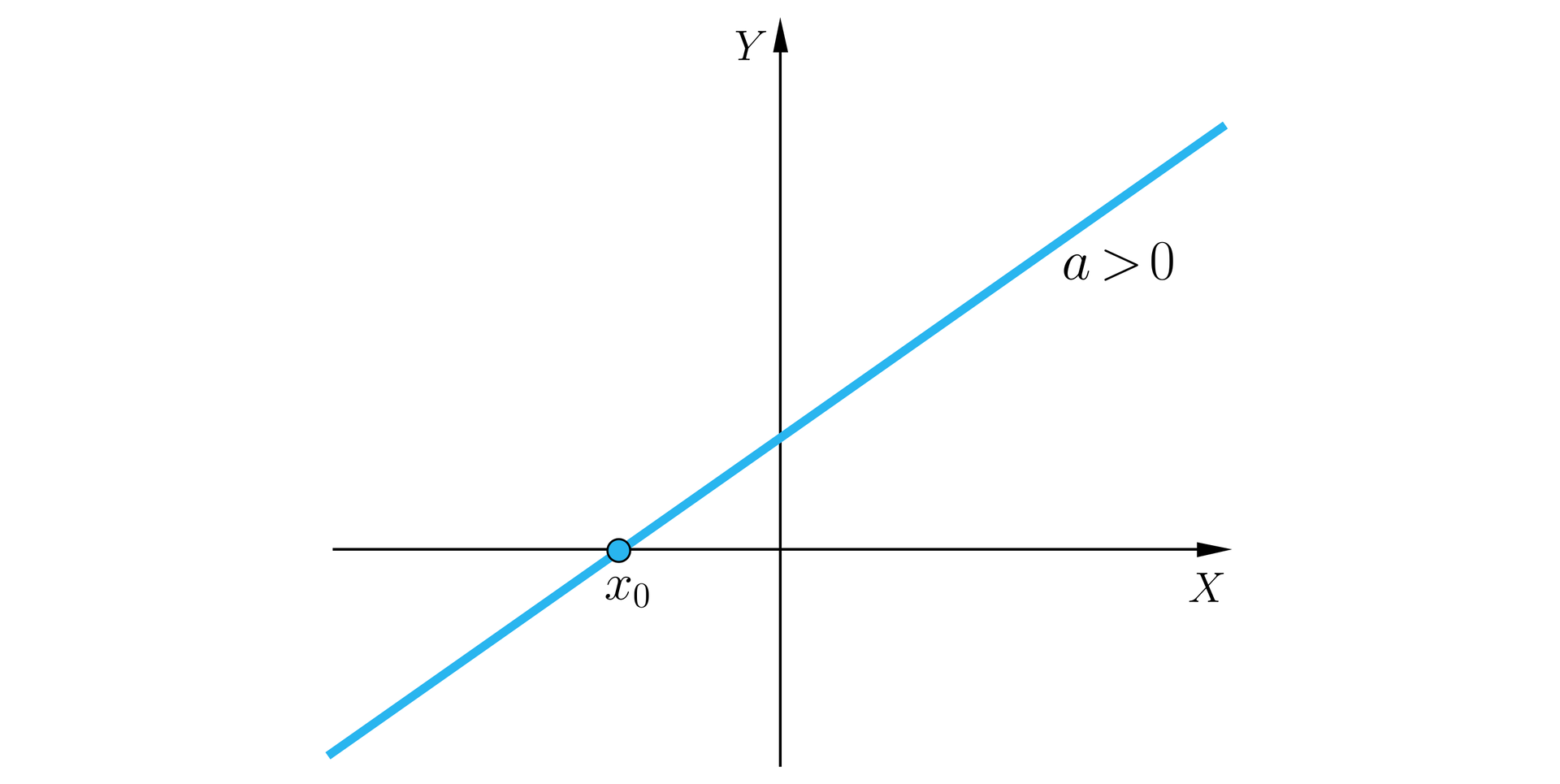
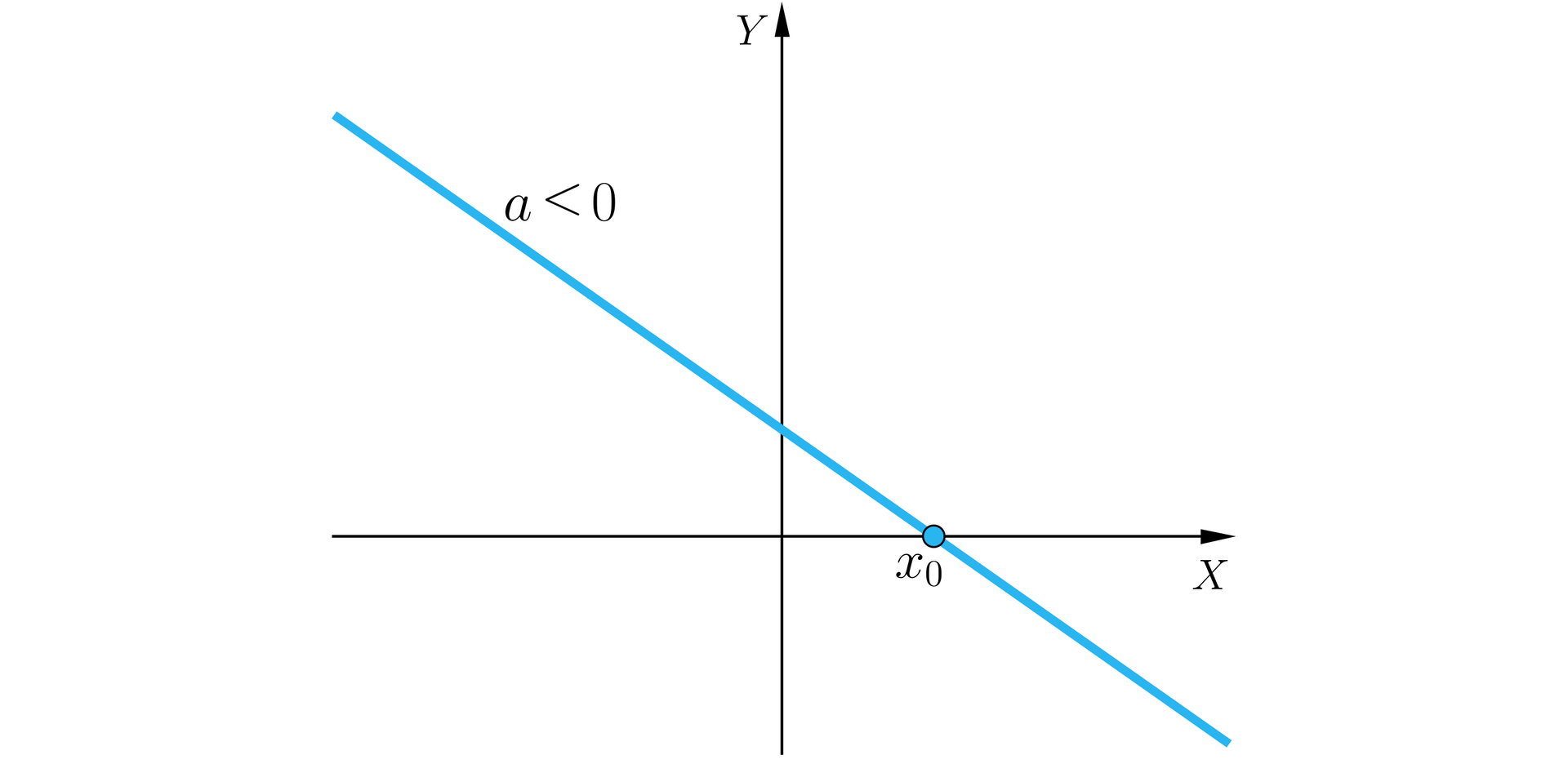
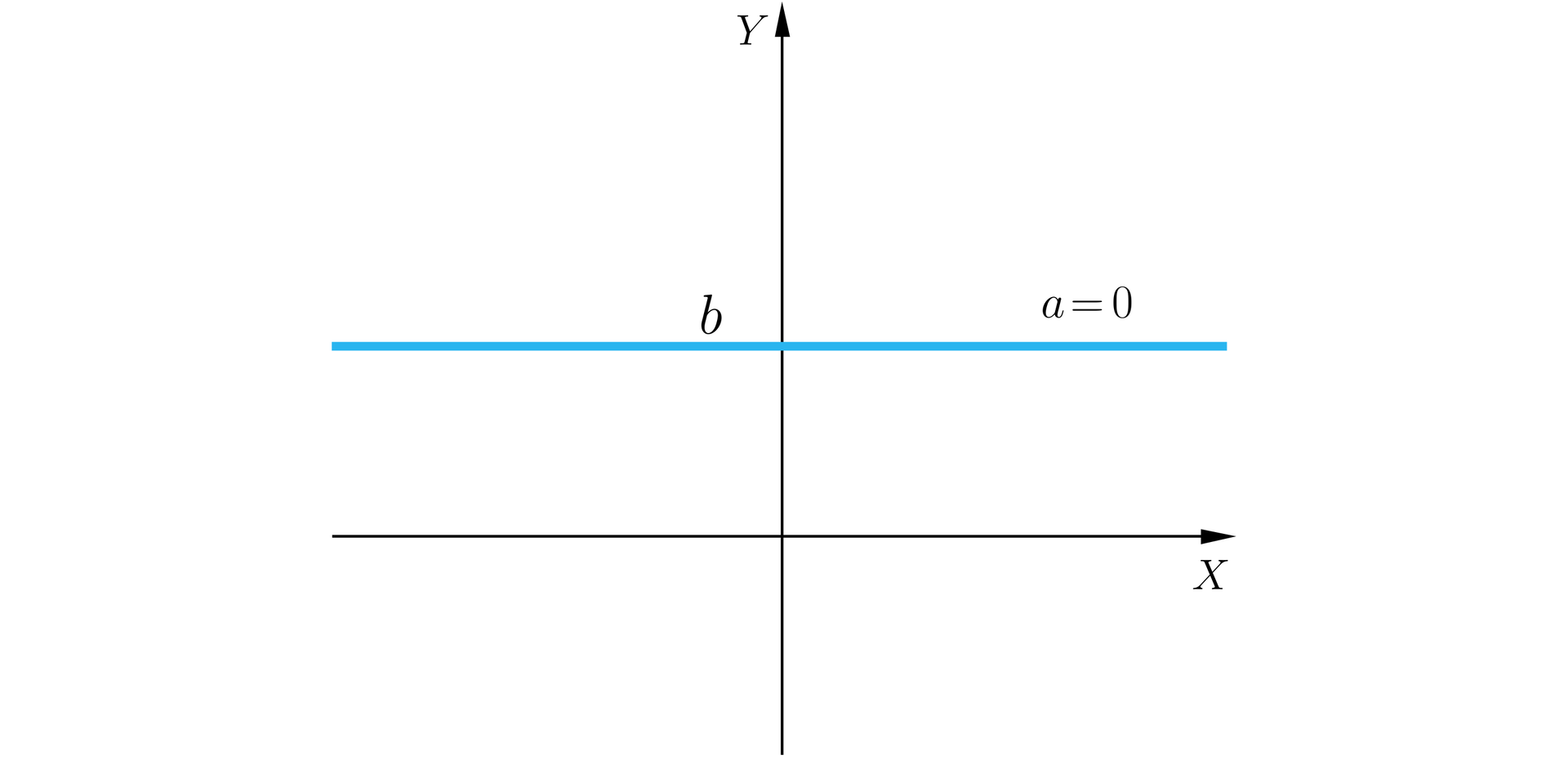
Przypomnijmy, że funkcję postaci , gdzie i są danymi liczbami rzeczywistymi nazywamy funkcją liniową.
Liczbę nazywamy współczynnikiem kierunkowym, – wyrazem wolnym.
Własności funkcji liniowej:
Mając dane dwa różne punkty możemy narysować tylko jedną prostą przechodzącą przez oba te punkty. Innymi słowy - dwa punkty jednoznacznie wyznaczają prostą. Jeśli wybrane punkty mają dodatkowo różne pierwsze współrzędne, możemy wyznaczyć wzór funkcji liniowej, która opisuje narysowaną prostą.
Napisz wzór funkcji liniowej, do wykresu której należą punkty: oraz .
Rozwiązanie:
Jeżeli punkt należy do wykresu funkcji liniowej , to znaczy, że współrzędne tego punktu spełniają równanie . Czyli
i
Jeżeli punkt należy do wykresu funkcji liniowej to znaczy, że współrzędne tego punktu spełniają równanie: .
Rozwiązujemy układ równań.
Odejmiemy stronami od pierwszego równania drugie .
, stąd
Wyznaczamy teraz wartość wyrazu wolnego z pierwszego równania.
Odpowiedź:
Szukana funkcja ma wzór .
Napisz wzór funkcji liniowej, mając dane jej miejsce zerowemiejsce zerowe i punkt , przez który przechodzi wykres tej funkcji.
Rozwiązanie (sposób ):
Miejsce zerowe funkcji to taki jej argument, dla którego przyjmuje ona wartość zero, czyli .
, więc , czyli .
Jeżeli punkt należy do wykresu funkcji liniowej to znaczy, że współrzędne tego punktu spełniają równanie .
i
Otrzymujemy układ równań z dwiema niewiadomymi i .
Tym razem wyznaczymy z pierwszego równania i podstawimy do drugiego .
Odpowiedź:
Wzór szukanej funkcji liniowej to .
Możemy też rozwiązać to zadanie, wykorzystując zależność między a współczynnikami i .
Rozwiązanie (sposób ):
Wyraźmy , miejsce zerowe funkcji liniowej, za pomocą współczynników i .
, przy założeniu: .
Punkt przecięcia z osią : .
, więc .
Punkt należy do wykresu funkcji .
Odpowiedź:
Wzór funkcji liniowej to .
Napisz wzór funkcji liniowej, której wykres przechodzi przez punkt i jest równoległy do wykresu funkcji .
Rozwiązanie:
Jeżeli proste i są równoległe, to .
Prosta jest równoległa do prostej , więc .
Równanie naszej prostej przyjmuje postać: .
Ponieważ wykres przechodzi przez punkt , to znaczy, że współrzędne tego punktu spełniają równanie .
Odpowiedź:
Wzór funkcji liniowej: .
Napisz wzór funkcji liniowej, której wykres tworzy z osią kąt o mierze i przecina oś w punkcie o współrzędnej .
Rozwiązanie:
Wykresem funkcji liniowej jest prosta nachylona do dodatniej półosi osi pod takim kątem , że .
Stąd .
Punkt przecięcia z osią to: .
(, stąd )
Ponieważ , to .
Odpowiedź:
Wzór funkcji liniowej: .
Znajdź wzór funkcji liniowejfunkcji liniowej, której wykres przechodzi przez punkt i która przyjmuje wartości dodatnie w przedziale , zaś ujemne w przedziale .
Rozwiązanie:
Funkcja przyjmuje wartości dodatnie w przedziale , zaś ujemne w przedziale , oznacza to, że jest miejscem zerowym tej funkcji.
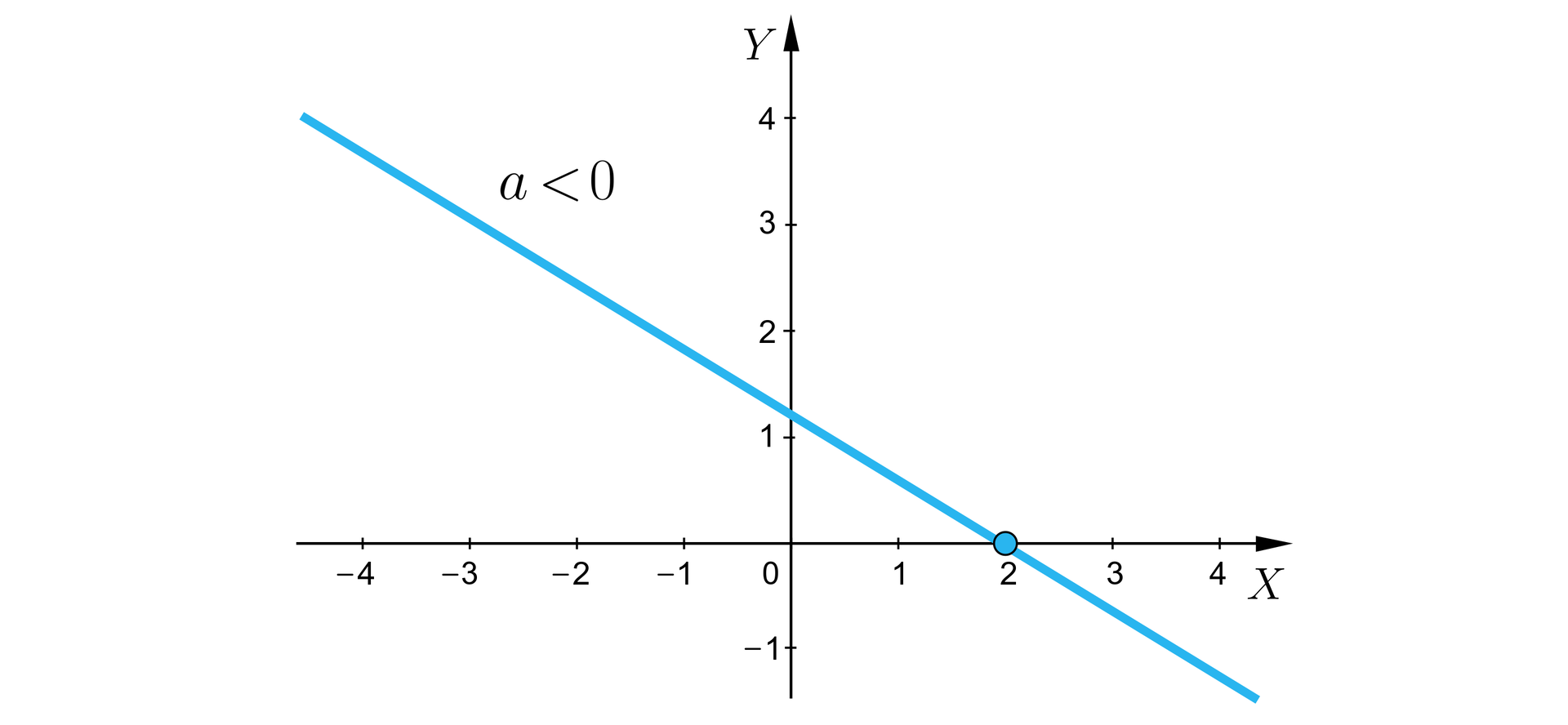
dla i dla .
Miejsce zerowe funkcji to taki jej argument, dla którego przyjmuje ona wartość zero, czyli taki , dla którego . Z wykresu możemy odczytać, że miejscem zerowym rozważanej funkcji jest . Możemy zatem wstawć punkt do równania funkcji:
.
Jeżeli punkt należy do wykresu funkcji liniowej to znaczy, że współrzędne tego punktu spełniają równanie: .
i
Otrzymujemy układ równań z dwiema niewiadomymi i .
Dodajemy stronami pierwsze równanie do drugiego.
Z pierwszego równania wyznaczamy .
Odpowiedź:
Wzór funkcji liniowej: .
Znajdź wzór funkcji liniowej , której wykres przechodzi przez punkt i która przyjmuje wartości dodatnie w przedziale , zaś ujemne w przedziale .
Rozwiązanie:
Funkcja przyjmuje wartości dodatnie w przedziale , zaś ujemne w przedziale , oznacza to, że jest miejscem zerowym tej funkcji i jest to funkcja rosnąca .
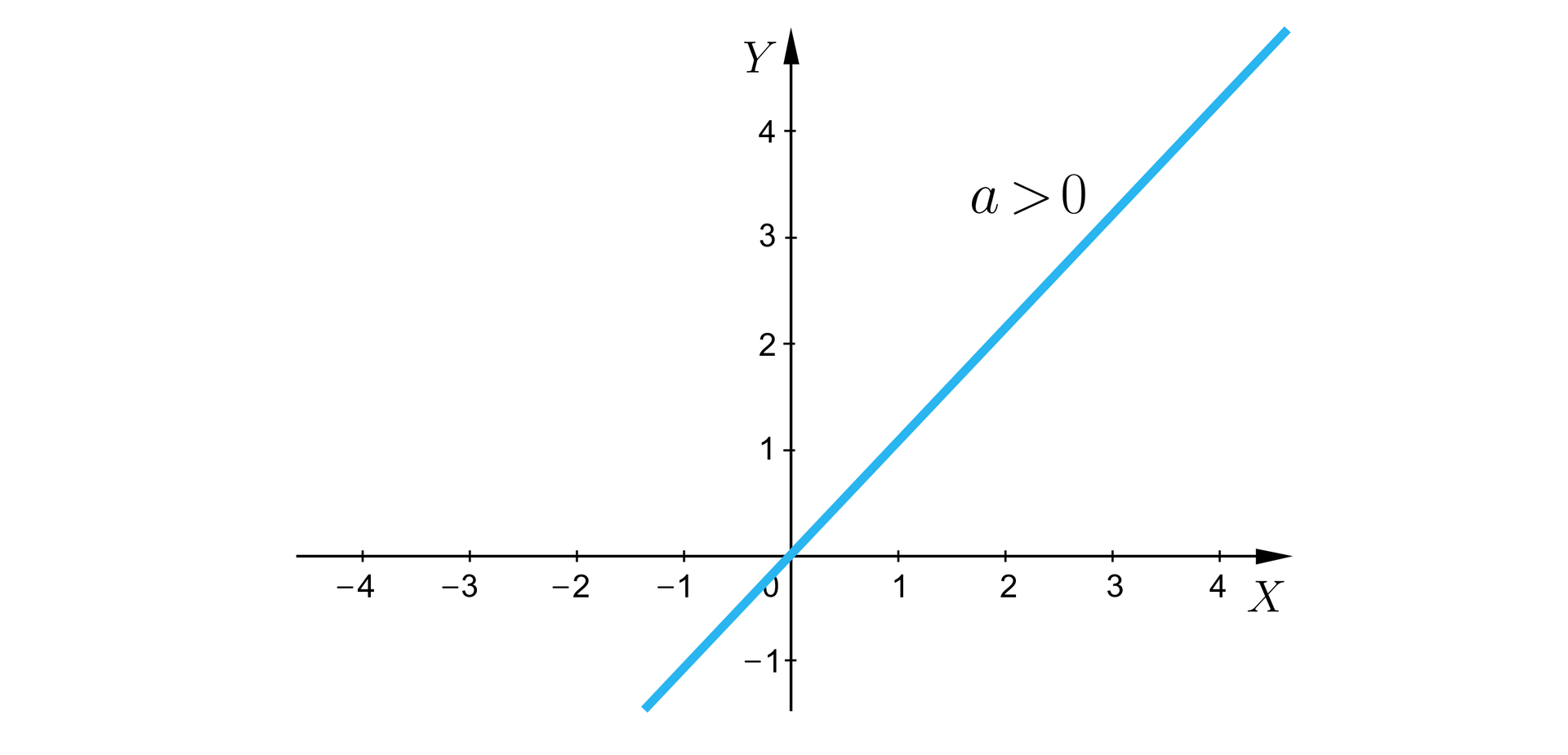
dla i dla .
, więc , czyli , stąd .
Punkt należy do wykresu funkcji liniowej , więc otrzymujemy .
, stąd otrzymujemy równanie . Rozwiązaniem równania są liczby: i .
Funkcja przyjmuje wartości dodatnie w przedziale , zaś ujemne w przedziale , funkcja jest rosnąca czyli , stąd .
,
Odpowiedź:
Wzór funkcji: .
Słownik
funkcja postaci , gdzie i są danymi liczbami rzeczywistymi
argument, dla którego funkcja przyjmuje wartość zero