Przeczytaj
Cosinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej przy tym kącie do długości przeciwprostokątnej.

Do oznaczenia funkcji cosinus używa się skrótu „cos”.
Stosując oznaczenia z rysunku mamy, że przyprostokątną leżącą przy kącie jest bok o długości a przyprostokątną leżącą naprzeciwko kąta jest bok o długości .
Zatem, zgodnie z definicją, mamy: oraz .
Z przyjętych oznaczeń wynika, że , więc .
Obliczymy wartości cosinusów kątów ostrych w trójkącie prostokątnym z rysunku.

Oznaczmy długość przeciwprostokątnej jako .
Z twierdzenia Pitagorasa otrzymujemy, że .
Z równania wynika, że , zatem lub .
Ponieważ , więc .
Z definicji funkcji cosinus otrzymujemy, że:
.
Dla dowolnego kąta ostrego zachodzi zależność:
Wyjaśnienie tej nierówności można zapisać w dwóch krokach:
nierówność wynika wprost z definicji funkcji cosinus w trójkącie prostokątnym,
ponieważ w dowolnym trójkącie prostokątnym długość przyprostokątnej jest zawsze mniejsza od długości przeciwprostokątnej, zatem:
.
Wyznaczymy wartości cosinusów niektórych kątów ostrych. Wykorzystamy do tego trójkąty charakterystyczne.
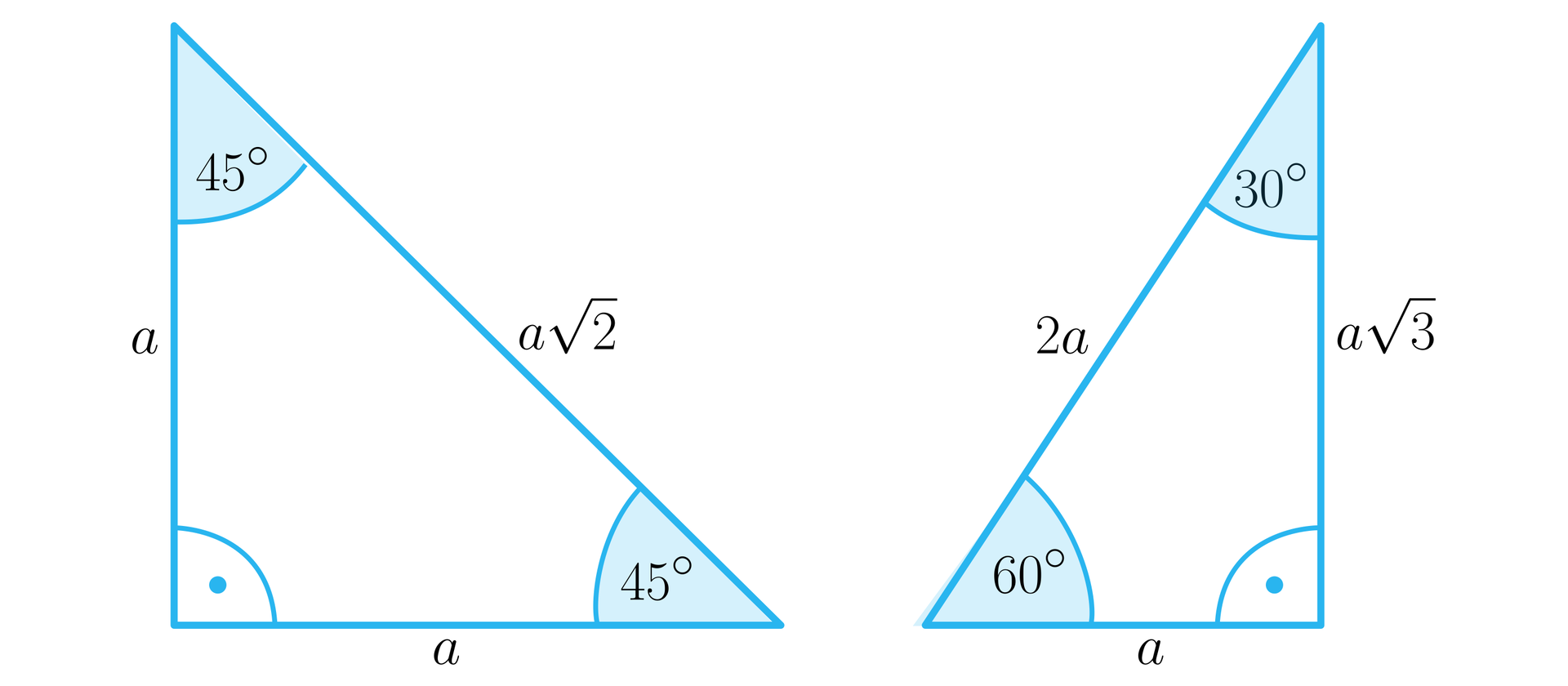
Korzystając z definicji funkcji cosinus, otrzymujemy, że:
Wyznaczymy wartość wyrażenia .
Po podstawieniu mamy:
.
Wiadomo, że suma cosinusów kątów ostrych w trójkącie prostokątnymcosinusów kątów ostrych w trójkącie prostokątnym wynosi . Obliczymy iloczyn cosinusów tych kątów.
Wprowadźmy oznaczenia, jak na rysunku.
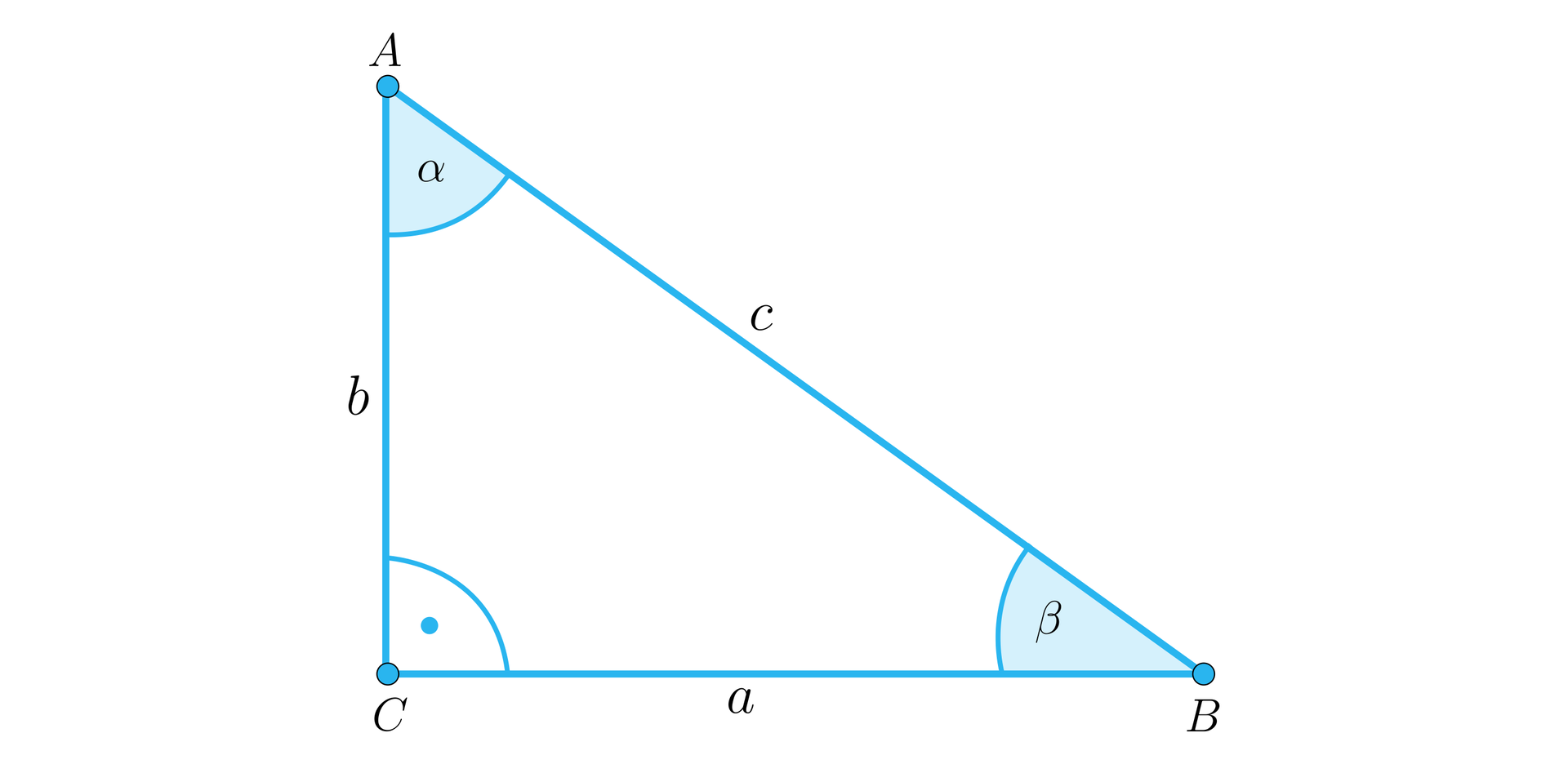
Z rysunku mamy, że oraz .
Wiadomo, że .
Stosując oznaczenia z rysunku, otrzymujemy równanie:
.
Podnosząc obie strony równania do kwadratu, mamy, że:
.
Po przekształceniu równanie jest postaci:
.
Z twierdzenia Pitagorasa wynika, że
, więc .
Równanie możemy zapisać w postaci .
Zatem , więc .
Po podstawieniu, zgodnie z wcześniejszymi oznaczeniami, otrzymujemy: .
Wyznaczymy długości przyprostokątnych w trójkącie prostokątnym o przeciwprostokątnej długości , jeżeli wiadomo, że cosinus jednego kąta ostrego jest dwa razy większy od cosinusa drugiego kąta ostrego.
Przyjmijmy oznaczenia jak na rysunku:
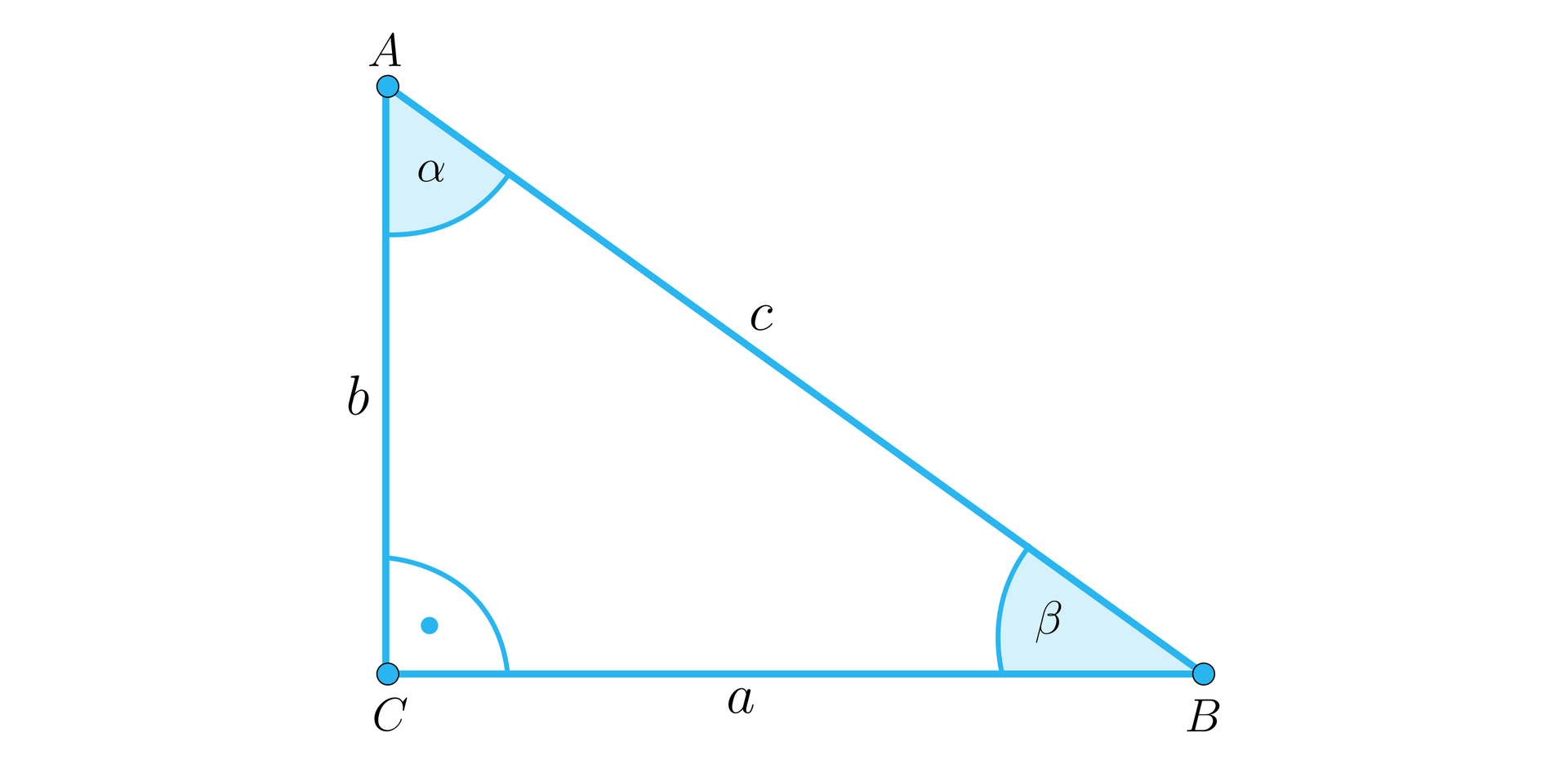
Z warunków zadania wynika, że oraz .
Z trójkąta prostokątnego z rysunku mamy, że oraz .
Po podstawieniu do zależności mamy, że:
, czyli .
Z twierdzenia Pitagorasa mamy, że
, więc .
Otrzymujemy równanie , zatem .
Przyprostokątne mają więc długości oraz .
Wykażemy, że jeżeli kąt jest ostry oraz , to .
Wprowadźmy następujące oznaczenia, jak na rysunku:
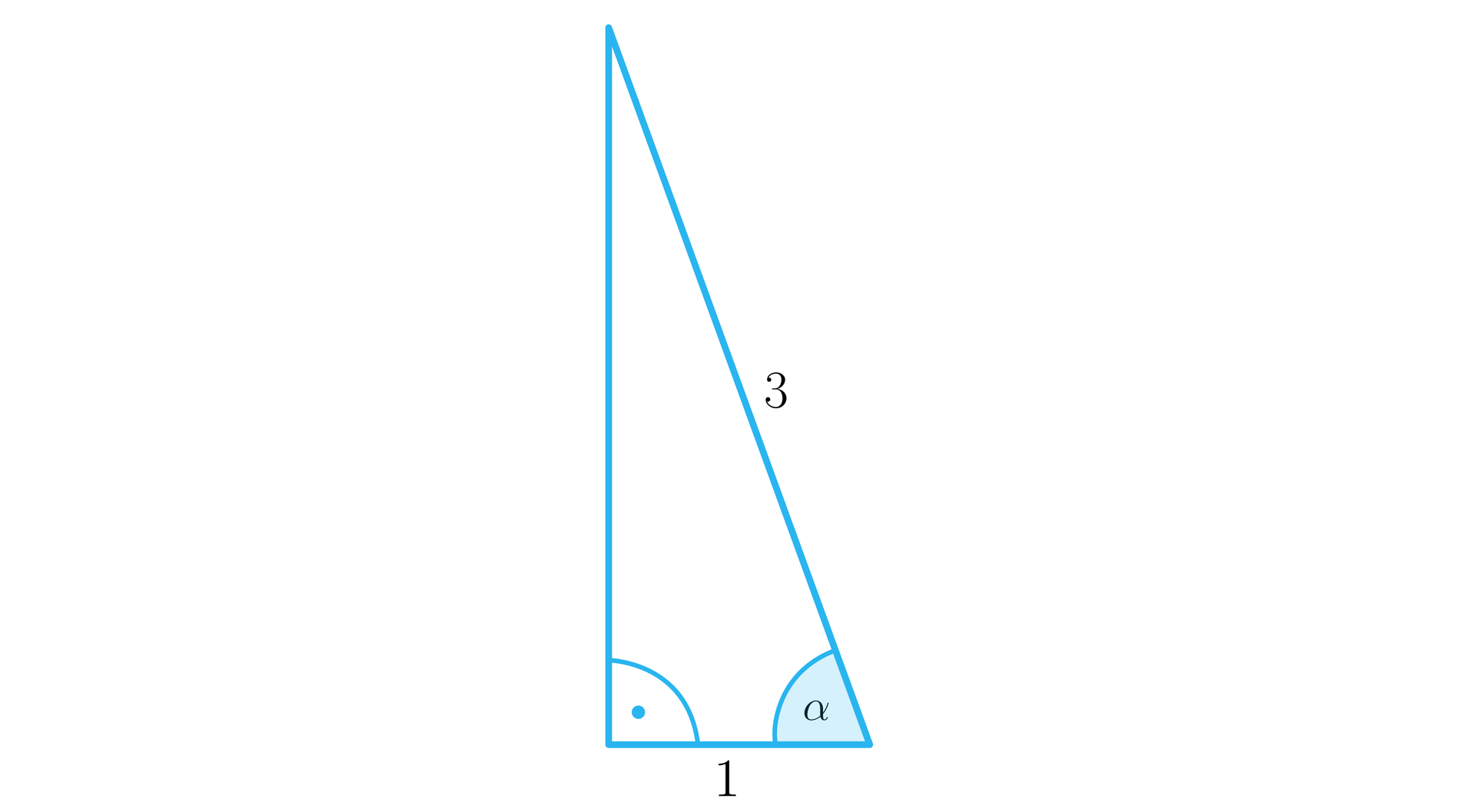
Z rysunku możemy odczytać, że .
Następnie dorysujmy, tak jak pokazano na rysunku, odcinek o długości oraz zaznaczmy kąt .
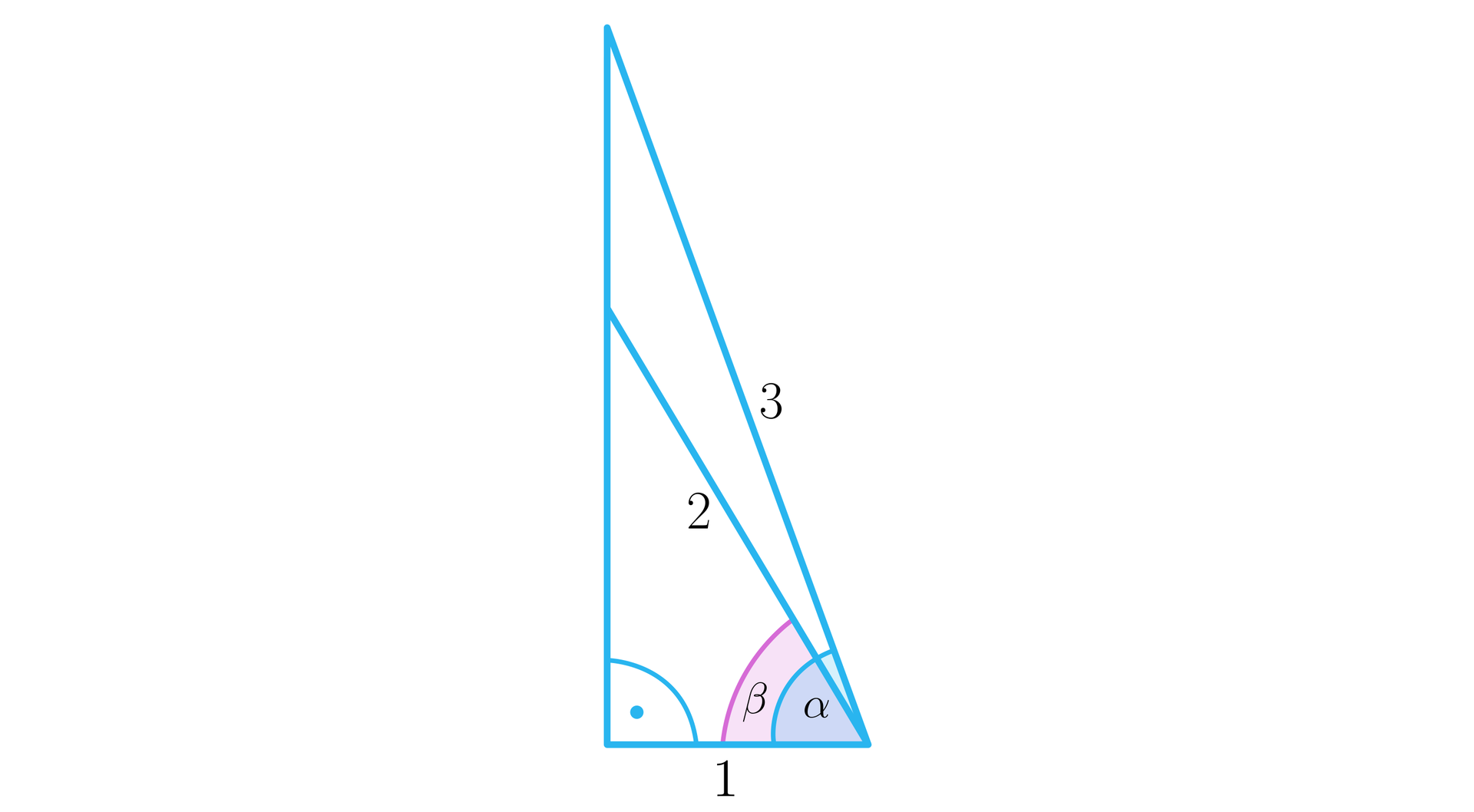
Z rysunku mamy, że , co oznacza że .
Ponieważ , więc .
Funkcja cosinus jest funkcją malejącą dla .
Słownik
stosunek długości przyprostokątnej leżącej przy kącie do długości przeciwprostokątnej