Dana jest funkcja $f$, której wykres znajduje się poniżej.

R1CsOjOnjQa8g

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Między zamalowanymi punktami $\left(1;4\right)$ oraz $\left(6;1\right)$. Pomiędzy punktami linią ciągłą narysowano kawałek krzywej f.

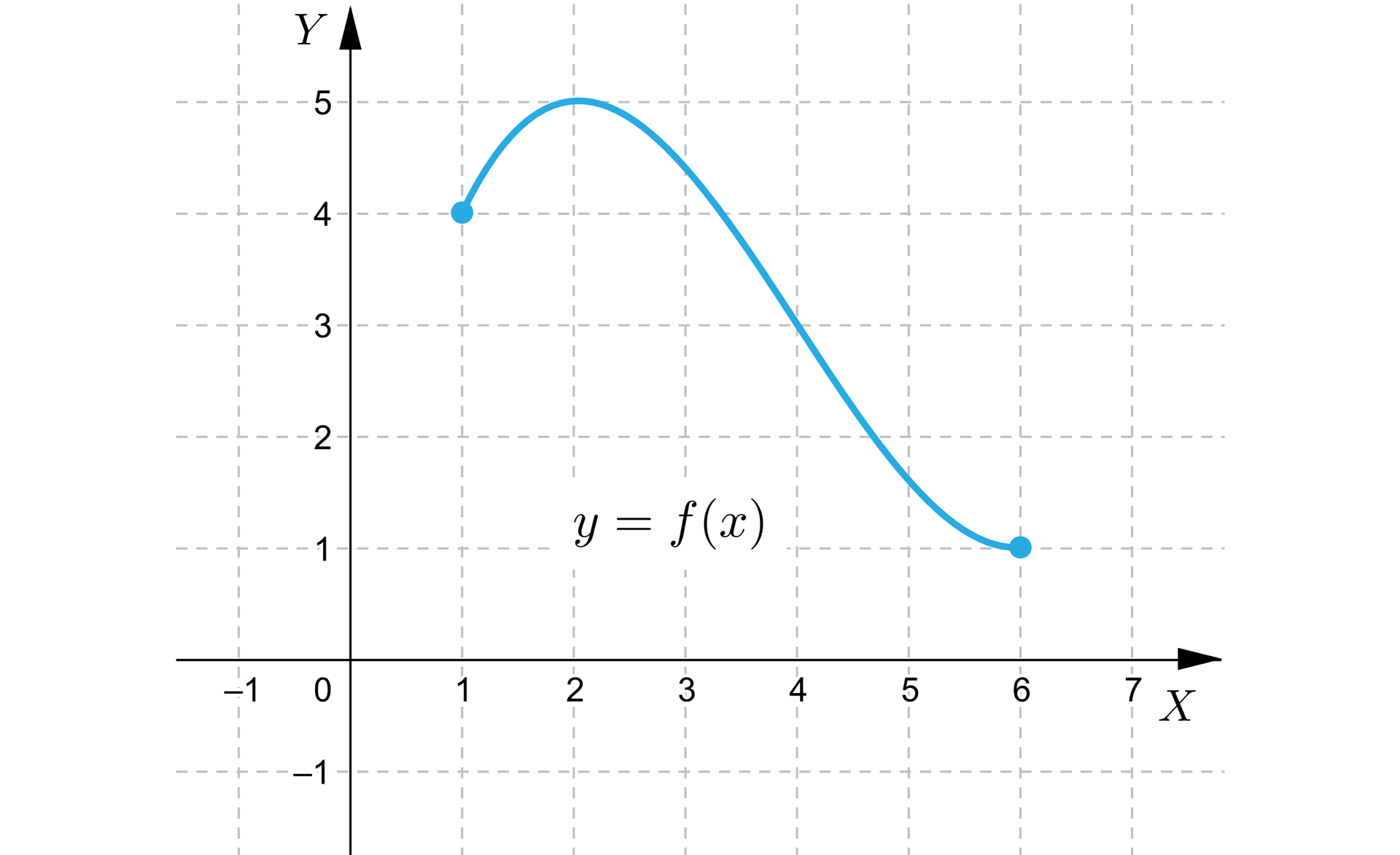
Zauważamy bez trudu, że wykres funkcji $f$ można narysować nie odrywając ołówka od kartki.

(Nieciągłość typu „skok”funkcja o nieciągłości typu „skok”Nieciągłość typu „skok”.)
Podamy przykład funkcji nieciągłej. Dana jest funkcja $f$ o następującym wykresie.

RdoTKs34R1njK

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 7, oraz pionową osią y od minus 1 do pięć. W układzie zaznaczono wykres funkcji o równaniu $y=f\left(x\right)$, składa się on z dwóch fragmentów. Pierwszy z  nich jest krzywą o kształcie łuku ograniczoną zamalowanymi punktami o współrzędnych nawias jeden średnik jeden zamknięcie nawiasu i nawias cztery średnik dwa zamknięcie nawiasu. Drugi fragment rozpoczyna się w niezamalowanym punkcie o współrzędnych nawias cztery średnik trzy zamknięcie nawiasu i biegnie ukośnie do zamalowanego punktu o współrzędnych nawias sześć średnik pięć zamknięcie nawiasu.

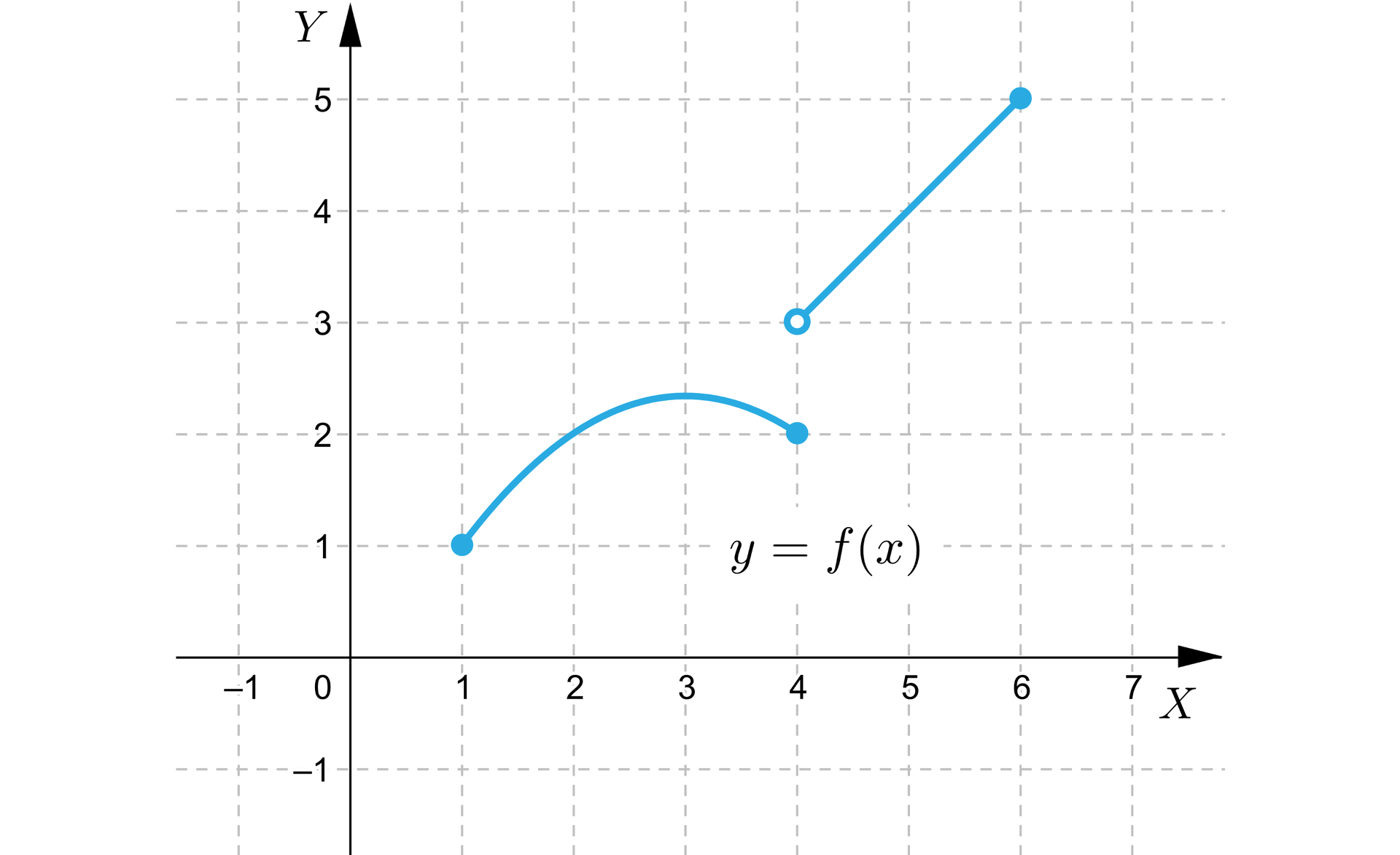
Zaczynając rysować wykres od strony lewej nie napotkamy żadnych problemów aż do punktu $4$. W tym miejscu ołówek rysujący wykres musi wykonać „skok”, podczas którego zostanie oderwany od podłoża.

(Nieciągłość typu „luka”funkcja o nieciągłości typu „luka”Nieciągłość typu „luka”.)
Pokażemy teraz inny przykład nieciągłości. Dana jest funkcja $f$ o wykresie

R1GrZdXBiXLOf

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 7, oraz pionową osią y od minus 1 do pięć. Na płaszczyźnie narysowano wykres funkcji f składający się z punktu oraz z krzywej w kształcie litery S ułożonej poziomo. Wykres rozpoczyna się w zamalowanym punkcie o współrzędnych nawias jeden średnik cztery zamknięcie nawiasu, następnie biegnie po łuku przez punkt nawias dwa średnik pięć zamknięcie nawiasu do niezamalowanego punktu nawias cztery średnik dwa zamknięcie nawiasu, dalej biegnie również po łuku do zamalowanego punktu nawias sześć średnik trzy zamkniecie nawiasu. Drugą częścią wykresu jest punkt nawias cztery średnik dwa zamknięcie nawiasu.

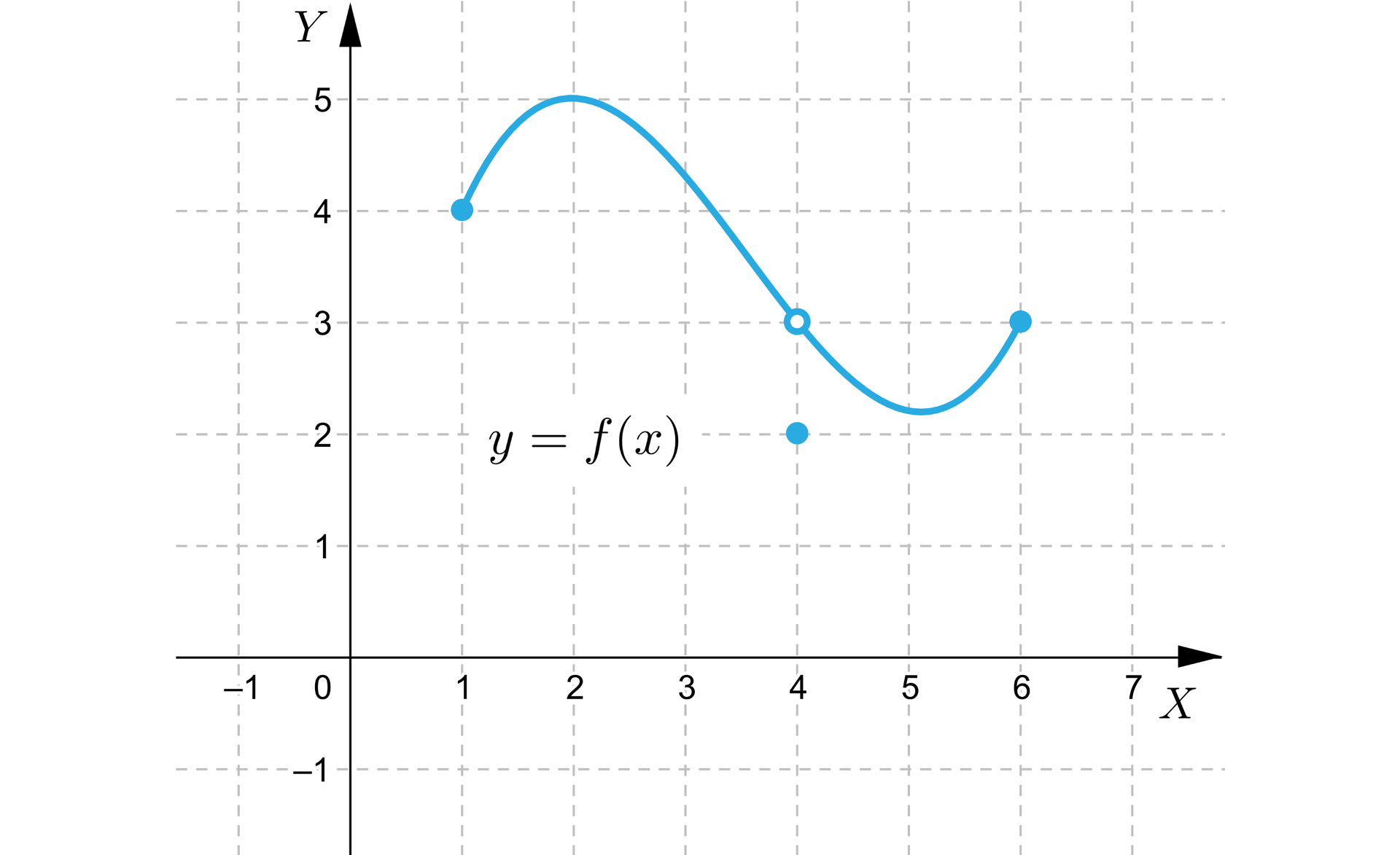
Podobnie jak w poprzednim przykładzie, kłopotliwy jest jedynie punkt $4$. Tym razem, problem stanowi jednak „luka”, którą rysujący wykres ołówek zmuszony jest przeskoczyć.

Funkcję $f$: $⟨a, b⟩⟶\mathrm{ℝ}$ nazywamy ciągłą, gdy dla każdego $x\in ⟨a, b⟩$

• istnieje granica (dla $x=a$ prawostronna, zaś dla $x=b$ lewostronna) funkcji $f$ w punkcie $x$ oraz

• granica ta wynosi $f\left(x\right)$.

Funkcja $f$: $D⟶\mathrm{ℝ}$ jest ciągła w punkcie $x_0\in D$, gdy dla każdego ciągu $\left(x_n\right)$ elementów $D$ zbieżnego do $x_0$ zachodzi

Mówimy, że funkcja $f$ jest ciągła, gdy jest ciągła w każdym punkcie swojej dziedziny.

Funkcję nazywamy parzystą, gdy jej wykres jest symetryczny względem osi $Y$.

Funkcję nazywamy nieparzystą, gdy jej wykres jest symetryczny względem początku układu współrzędnych.

Łatwo się przekonać, że wykres funkcji $f\left(x\right)=x-3$ nie jest symetryczny względem osi $Y$. Funkcja ta nie jest zatem parzysta. Nie jest jednak nieparzysta, gdyż wykres $f$ nie jest symetryczny również względem początku układu współrzędnych.

Otrzymujemy zatem, że funkcja, która nie jest parzysta nie musi być nieparzysta. Analogiczna sytuacja nie może mieć miejsca w przypadku ciągłości funkcji. Innymi słowy, każda funkcja jest albo ciągła, albo nieciągła.

Podamy przykład funkcji ciągłej, która wymyka się podanej na początku, intuicyjnej definicji. Dana jest funkcja $f$ o następującym wykresie

RuH1c7l4kjse1

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 7, oraz pionową osią y od minus 1 do pięć. Na płaszczyźnie narysowano wykres funkcji f składający się z dwóch krzywych. Pierwsza z nich rozpoczyna się w zamalowanym, którego współrzędna x ma wartość jeden, a współrzędna y znajduje się pomiędzy wartością 4 i pięć, następnie biegnie do punktu nawias trzy średnik trzy. Drugi fragment rozpoczyna się w zamalowanym punkcie nawias cztery średnik trzy zamknięcie nawiasu i biegnie przez punkt nawias pięć średnik dwa zamknięcie nawiasu do zamalowanego punktu, którego współrzędna x ma wartość 6, a wartość y znajduje się pomiędzy wartością 3 i cztery.

Możemy z łatwością zaobserwować, że funkcja $f$ jest ciągła w każdym punkcie swojej dziedziny. Nie jest jednak możliwe, by narysować wykres funkcji $f$ bez odrywania ołówka od kartki.

Pokażemy przykład funkcji ciągłej, której wykres wydaje się rozrywać. Dana jest funkcja $f\left(x\right)=\frac{1}{x}$. Jej dobrze znany wykres

Rbx5Cgox6OdBY

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do czterech oraz z pionową osią Y od minus trzech do trzech. Na płaszczyźnie narysowano hiperbolę, której części znajdują się w pierwszej i w trzeciej ćwiartce. Lewa część hiperboli przechodzi przez punkt nawias minus jeden średnik minus jeden, a prawa część hiperboli przechodzi przez punkt nawias jeden średnik jeden zamknięcie nawiasu.

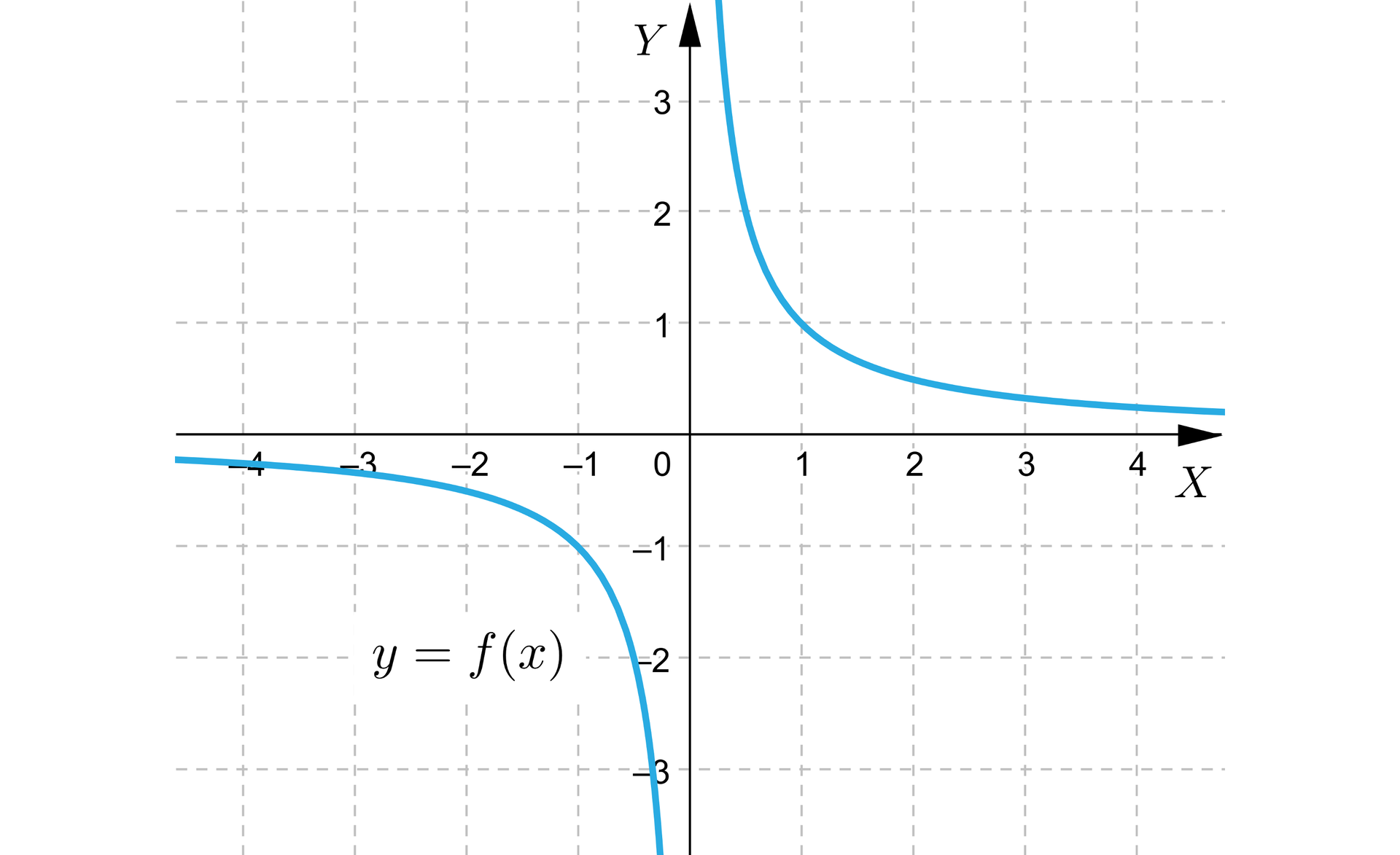
„rozrywa się” w punkcie $0$. Powstaje jednak niemały problem. Dziedziną funkcji $f$ jest zbiór $\mathrm{ℝ}\setminus \left\{0\right\}$, a więc funkcja $f$ w ogóle nie jest określona w zerze. Tym bardziej nie może być tam ciągła lub nieciągła. Jeżeli zaś weźmiemy jakikolwiek inny punkt $x\ne 0$, to bez trudu zauważymy, że funkcja $f$ jest ciągła w tym punkcie.

R19FMJYqBfrBf

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do czterech oraz z pionową osią Y od minus trzech do trzech. Na płaszczyźnie narysowano hiperbolę, której części znajdują się w pierwszej i w trzeciej ćwiartce. Lewa część hiperboli przechodzi przez punkt nawias minus jeden średnik minus jeden, a prawa część hiperboli przechodzi przez punkt nawias jeden średnik jeden zamknięcie nawiasu. Na osi x zaznaczono punkt znajdujący się pomiędzy wartością zero i jeden, z tego punktu biegnie pionowa linia przerywana aż do punktu leżącego na hiperboli.

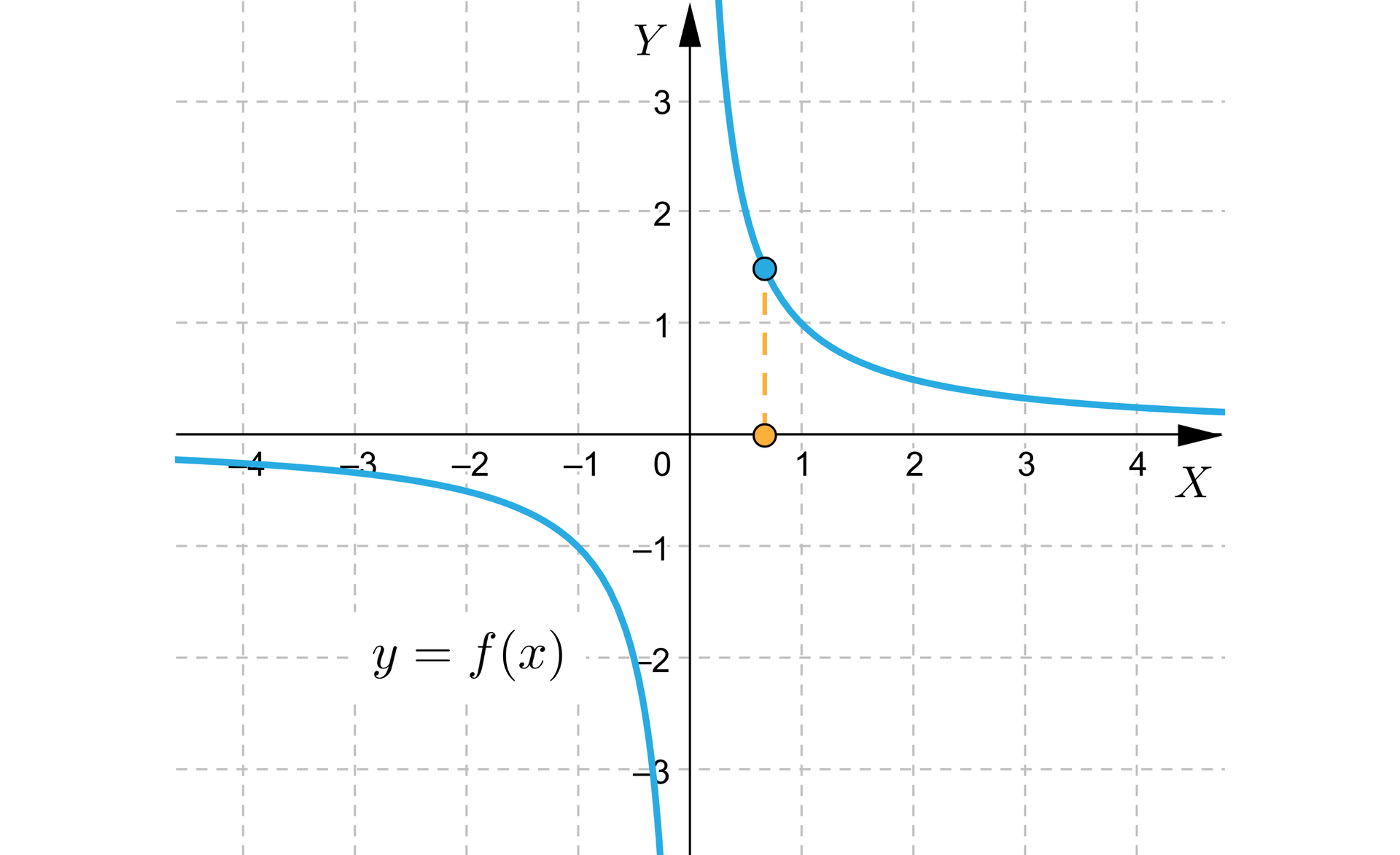
Nie ulega więc wątpliwości, że funkcja $f$ jest ciągła jako funkcja ciągłafunkcja ciągłafunkcja ciągła w każdym punkcie swojej dziedziny.

Pokażemy, że funkcja z przykładu 5 staje się nieciągła, gdy tylko włączymy zero do jej dziedziny. Rozważamy funkcję

$f\left(x\right)=\left\{\begin{array}{ll}{\displaystyle \frac{1}{x},}& \text{gdy }x\ne 0\\ 0,& \text{gdy }x=0\end{array}\right.$.

Teraz funkcja $f$ jest już określona dla wszystkich liczb rzeczywistych, w tym dla punktu $0$. Wykres wciąż rozrywa się w zerze.

R1KjDcWW6INwK

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do czterech oraz z pionową osią Y od minus trzech do trzech. Na płaszczyźnie narysowano hiperbolę, której części znajdują się w pierwszej i w trzeciej ćwiartce. Lewa część hiperboli przechodzi przez punkt nawias minus jeden średnik minus jeden, a prawa część hiperboli przechodzi przez punkt nawias jeden średnik jeden zamknięcie nawiasu. Środek układu współrzędnych zaznaczono zamalowanym punktem.

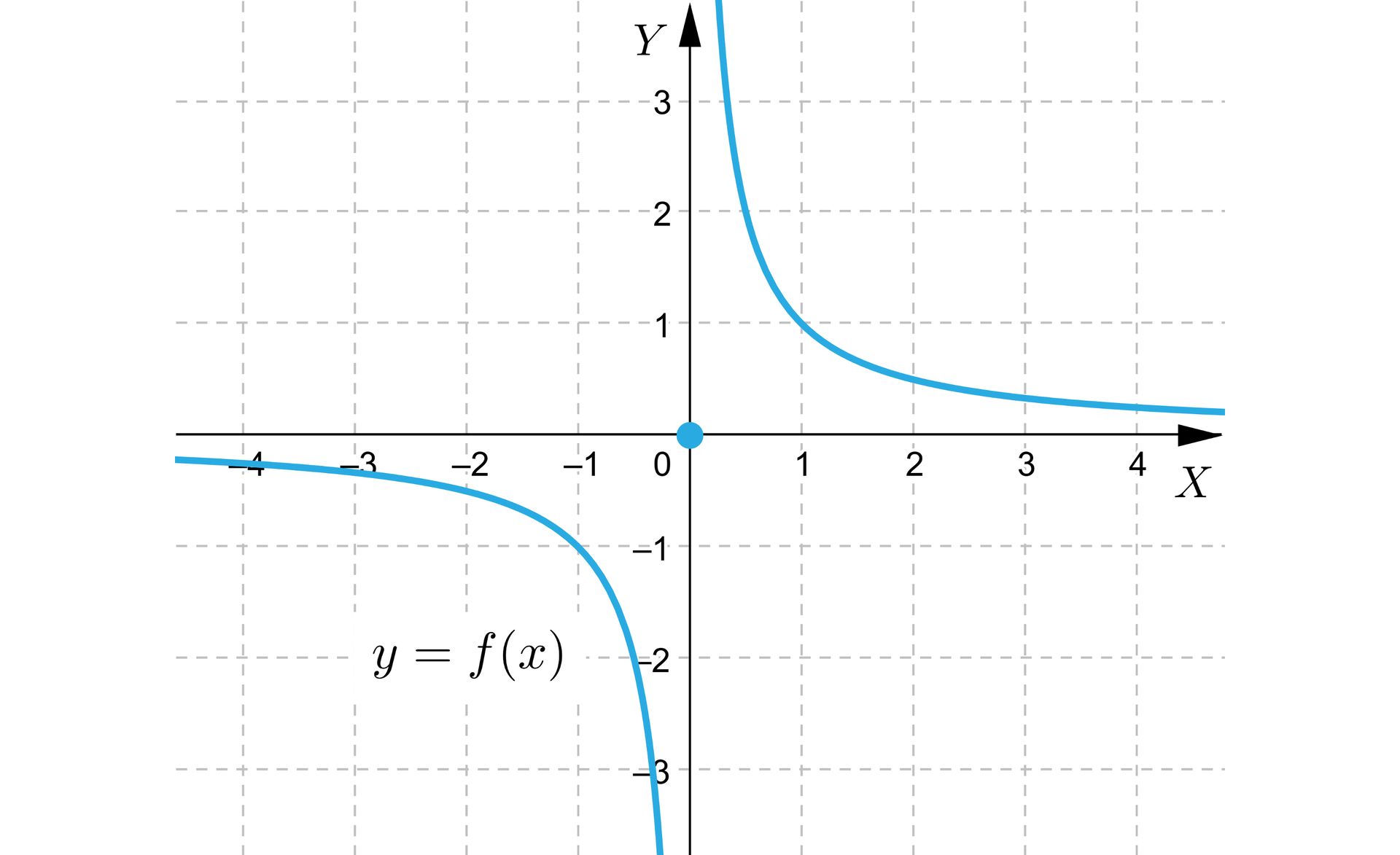
Tym samym funkcja $f$ jest nieciągła w zerze. Co za tym idzie, jest ona nieciągła. Zwróćmy uwagę, że nie da się przyjąć żadnej wartości w punkcie $0$ tak, by funkcja $f$ była ciągła.

funkcja ciągła w każdym punkcie dziedziny

funkcja, która w pewnym punkcie swej dziedziny posiada skończone, lecz różne granice lewostronną i prawostronną

funkcja, która w pewnym punkcie swej dziedziny posiada granicę różną od wartości funkcji w tym punkcie