Przeczytaj
Symetralna odcinka
Symetralną odcinka nazywamy taką prostą , która przechodzi przez środek odcinka i jest do niego prostopadła.
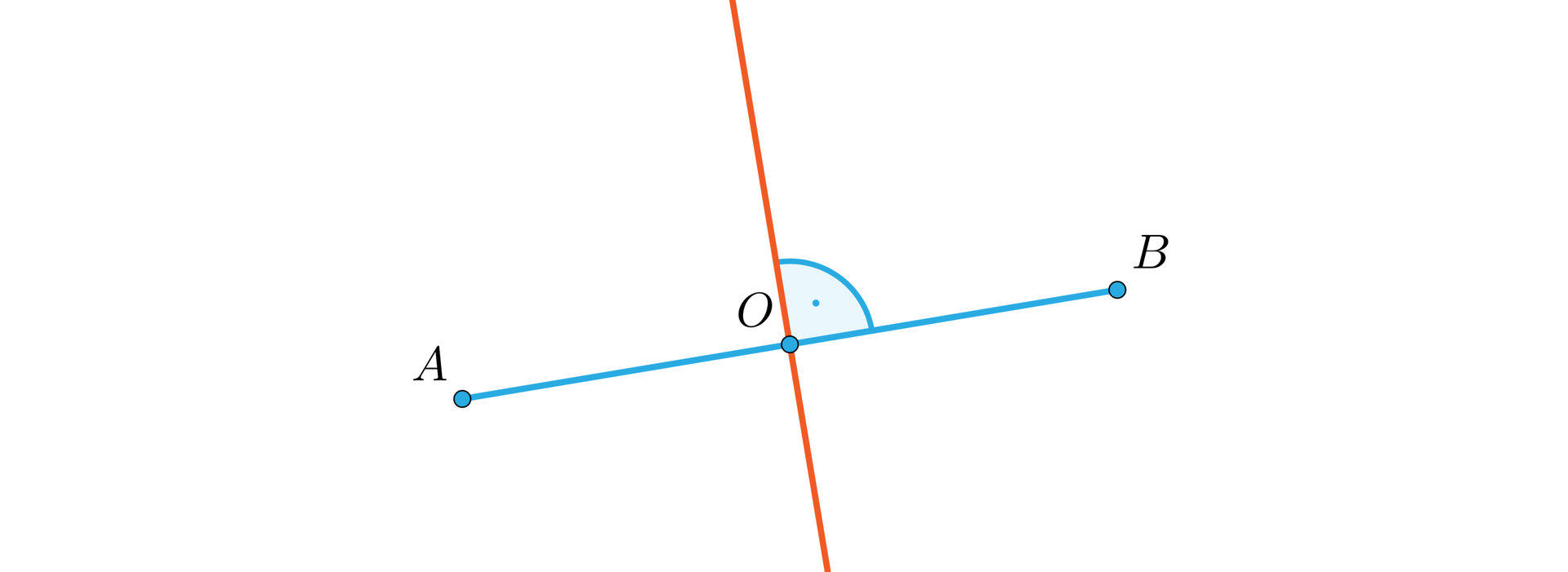
Przypomnimy poniżej bardzo ważne twierdzenie o symetralnej odcinka.
Symetralna odcinka jest zbiorem wszystkich punktów płaszczyzny równo oddalonych od jego końców.
Skonstruujemy trójkąt równoramienny wykorzystując powyższe twierdzenie.
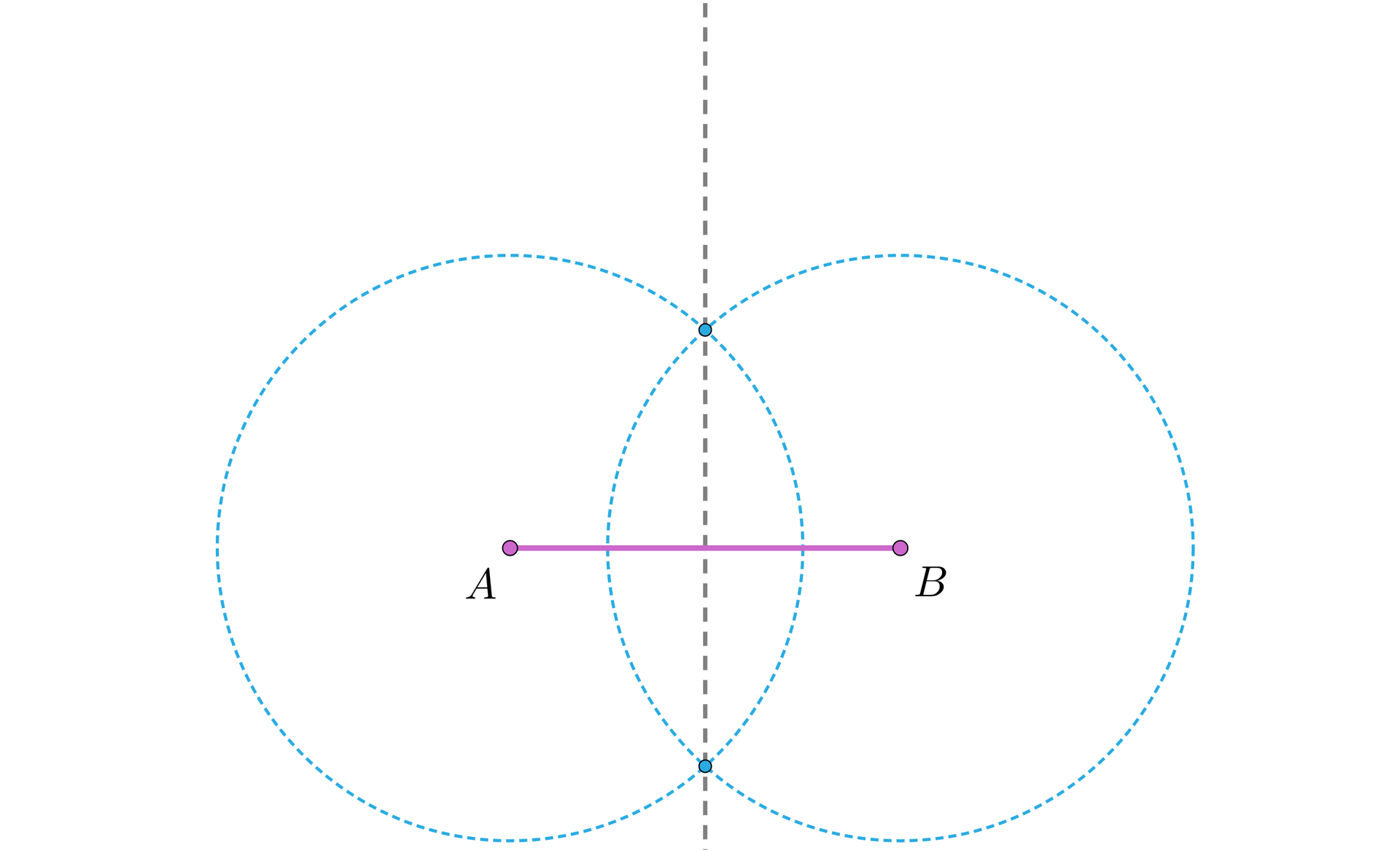
Rozwiązanie
Wykorzystując fakt, że punkt leżący na symetralnej odcinkasymetralnej odcinka jest równo odległy od końców odcinka, możemy w dowolny sposób skonstruować trójkąt równoramienny wybierając wierzchołek na symetralnej odcinka . Wtedy .
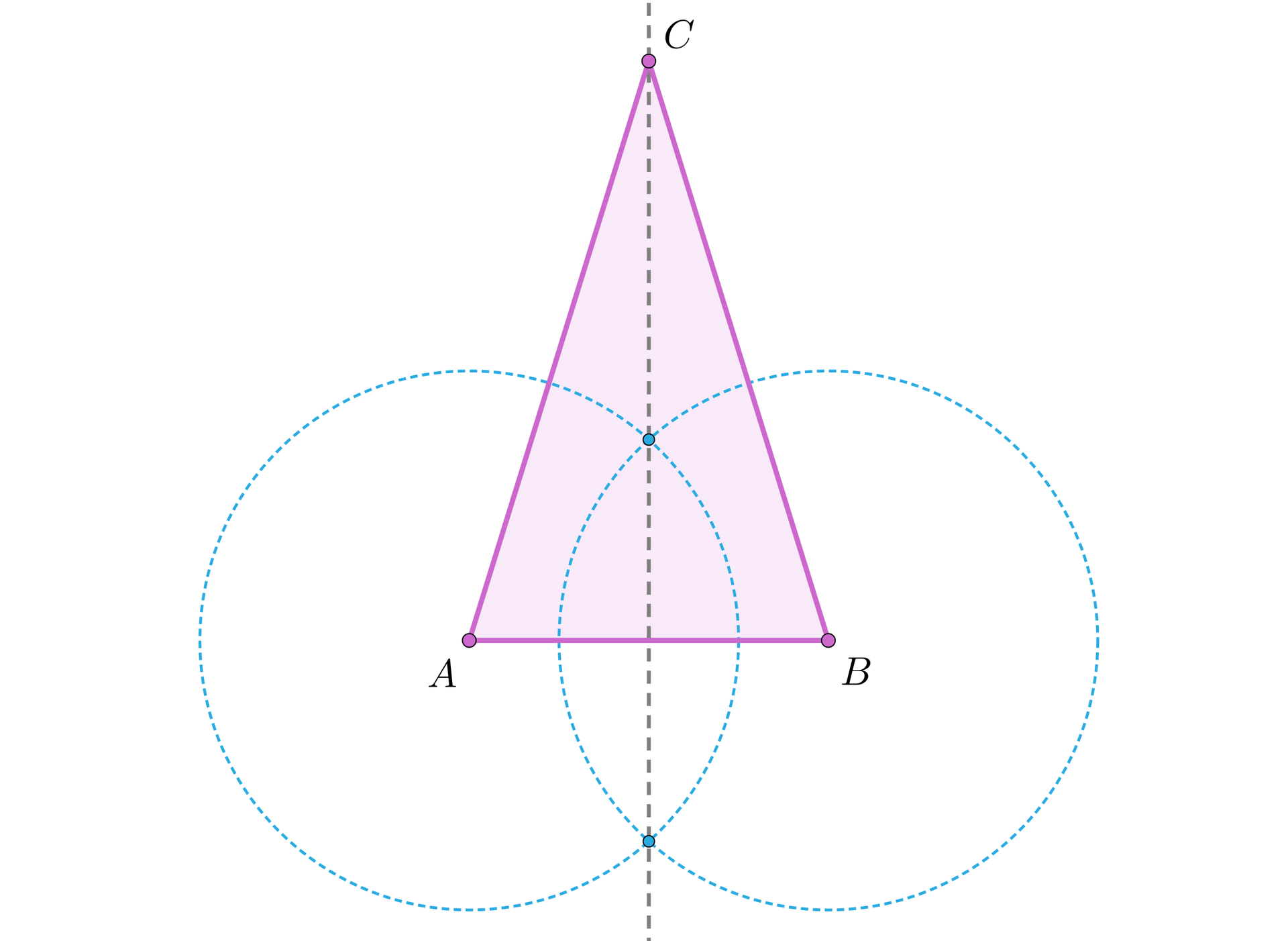
Symetralne boków trójkąta
Skonstruujemy symetralne boków trójkąta ostrokątnego.
Rozwiązanie
Przypomnijmy schemat konstrukcji symetralnej odcinka:
Z obu końców odcinka kreślimy łuki o równych promieniach. Łuki te przecinają się w punktach.
Przez wyznaczone punkty prowadzimy prostą – jest ona symetralną tego odcinka.

Zauważmy, że symetralne boków trójkąta ostrokątnego przecinają się w punkcie, który leży wewnątrz tego trójkąta.
Skonstruujemy symetralne boków trójkąta prostokątnego.
Rozwiązanie
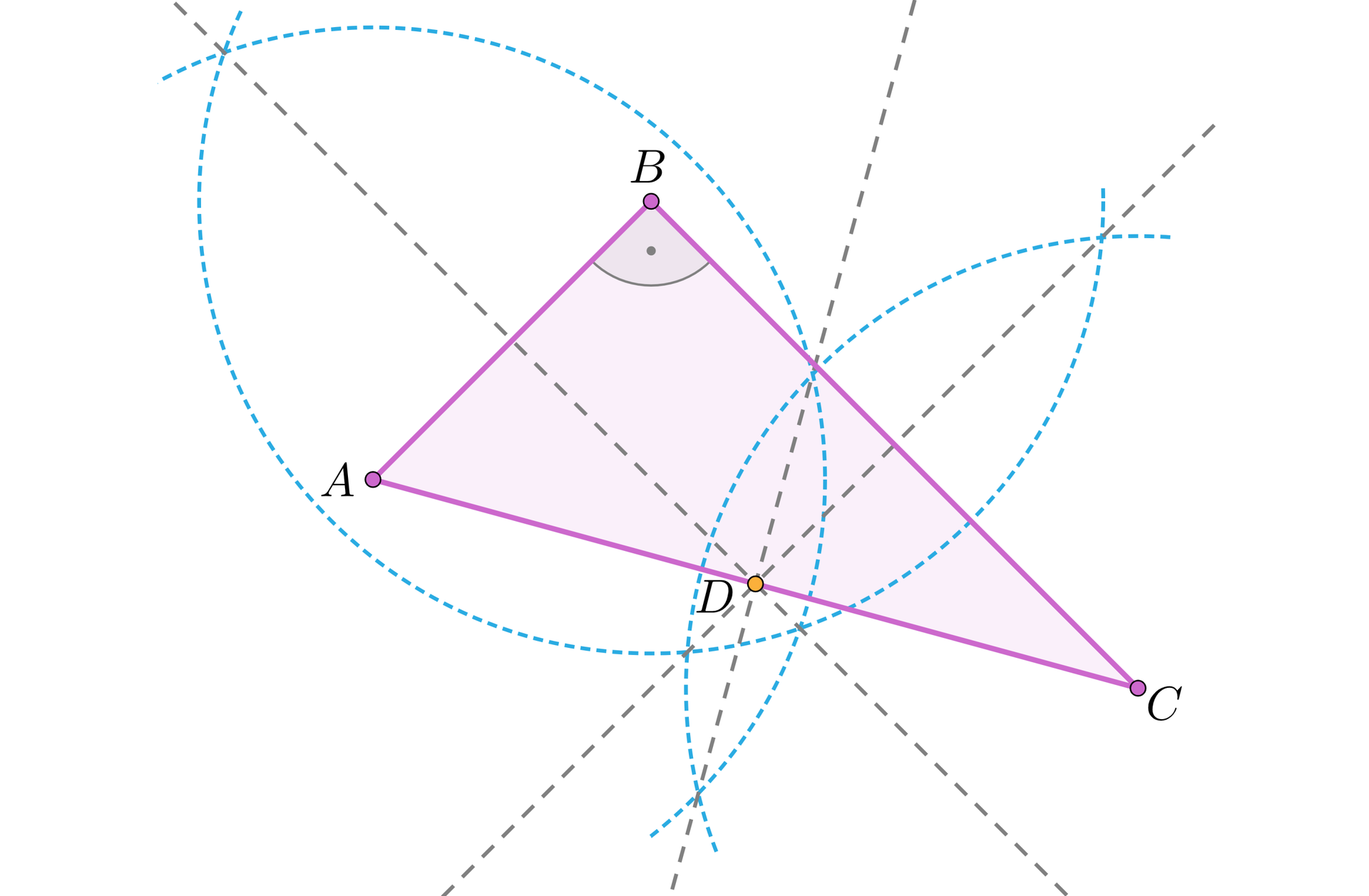
Zauważmy, że symetralne boków trójkąta prostokątnego przecinają się w punkcie, który leży na jego przeciwprostokątnej.
Udowodnimy, że punkt przecięcia symetralnych boków trójkąta prostokątnego jest środkiem przeciwprostokątnej.
Rozwiązanie
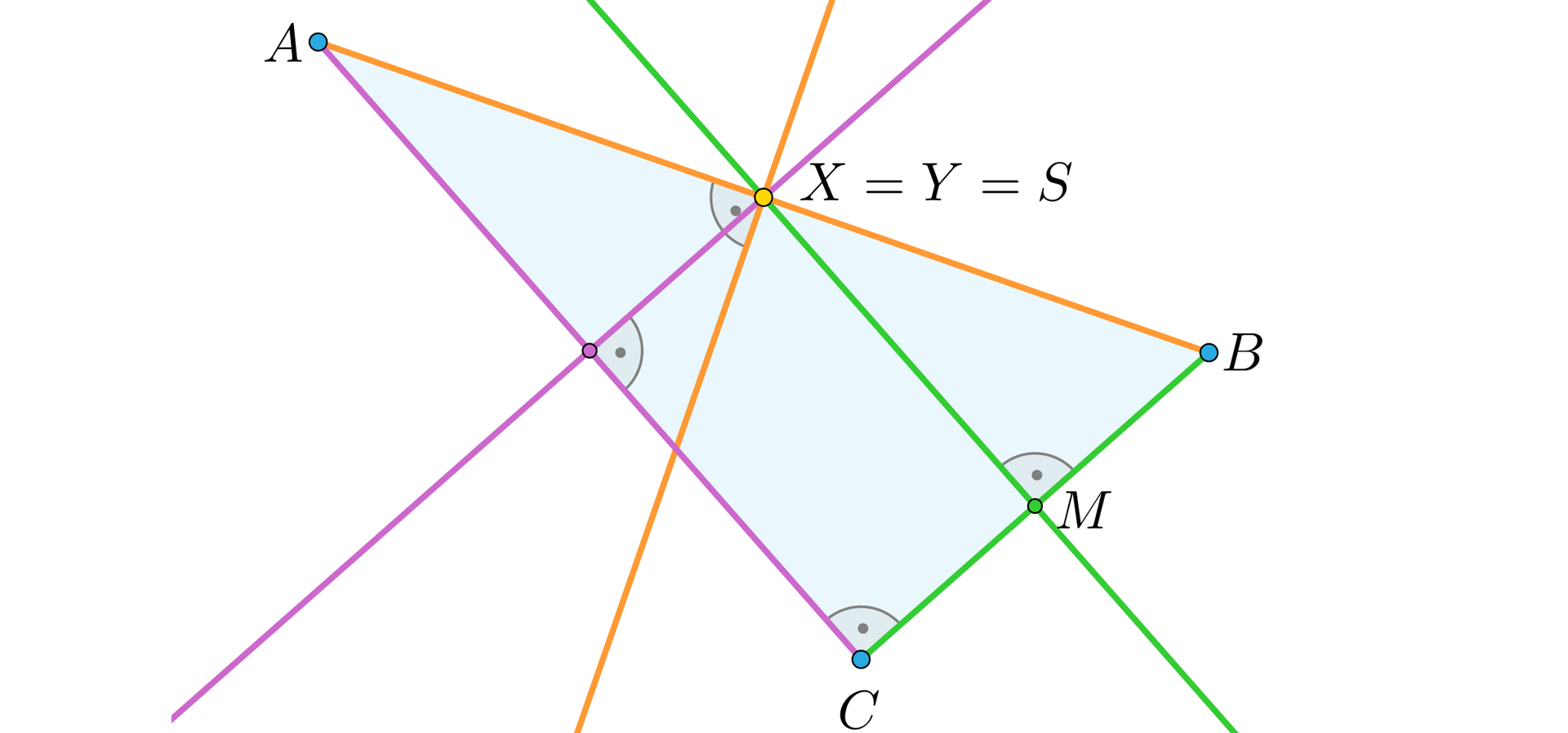
Niech dany będzie trójkąt prostokątny , gdzie kąt prosty znajduje się przy wierzchołku i niech będzie punktem przecięcia symetralnych boków. Oznaczmy przez środek odcinka . Oznaczmy również przez przecięcie symetralnej odcinka z przeciwprostokątną .
Wiadomo, że i , a zatem proste i są równoległe, tj. . Wynika stąd, z zasady zachowania kątów (cecha KKK), że trójkąty i są podobne.
Zauważmy, że skoro , to trójkąt jest dwa razy większy od trójkąta (skala podobieństwa wynosi ). Z tego faktu wprost wynika, że .
Oznaczając przez przecięcie symetralnej odcinka z przeciwprostokątną analogicznie otrzymamy, że .
Ostatecznie skoro i oraz z faktu, że punkty , leżą na przeciwprostokątnej wynika, że , gdzie jest środkiem odcinka co kończy dowód.
Skonstruujemy symetralne boków trójkąta rozwartokątnego.
Rozwiązanie
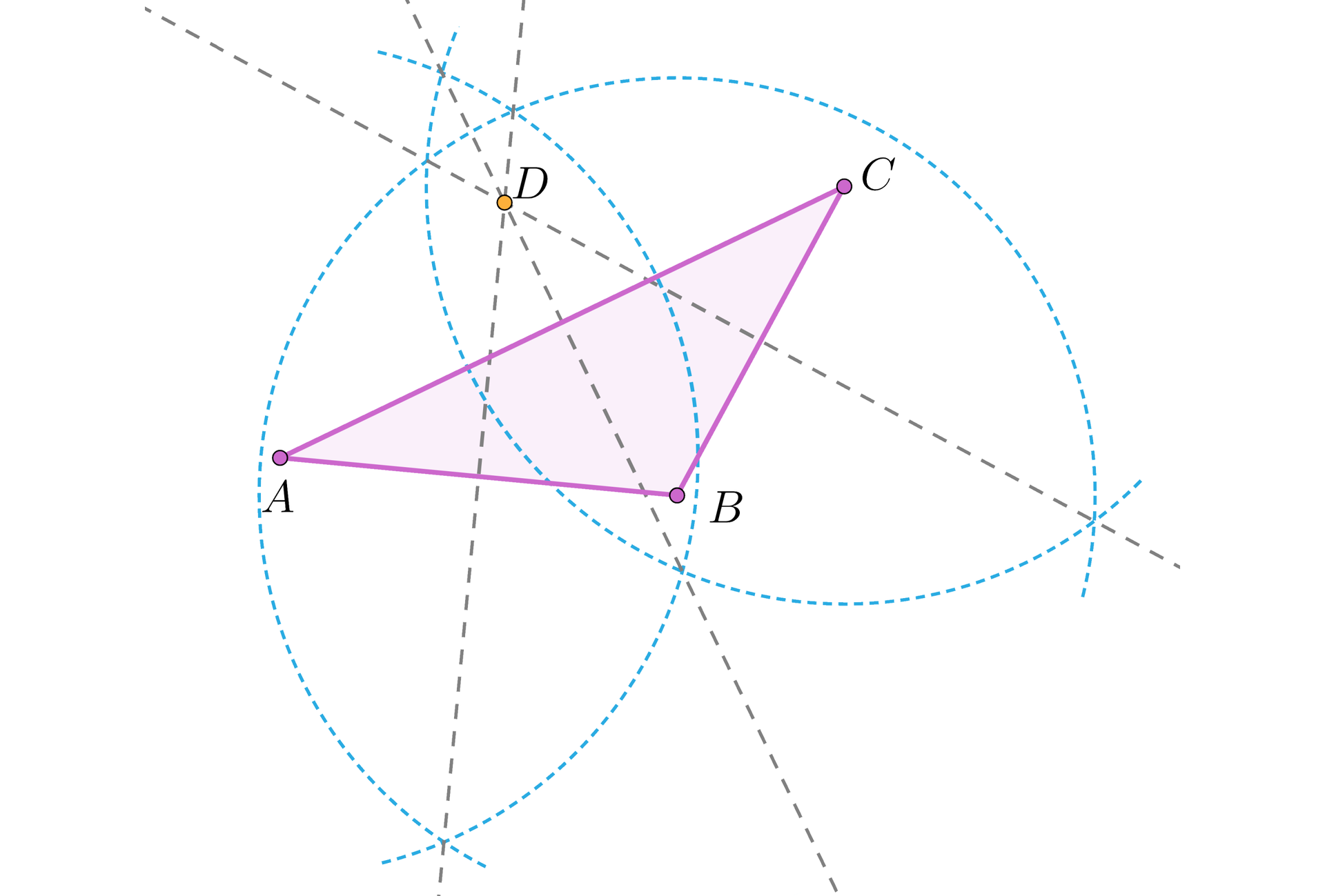
Zauważmy, że symetralne boków trójkąta rozwartokątnego przecinają się w punkcie, który leży na zewnątrz tego trójkąta.
Symetralne boków trójkąta przecinają się w jednym punkcie.

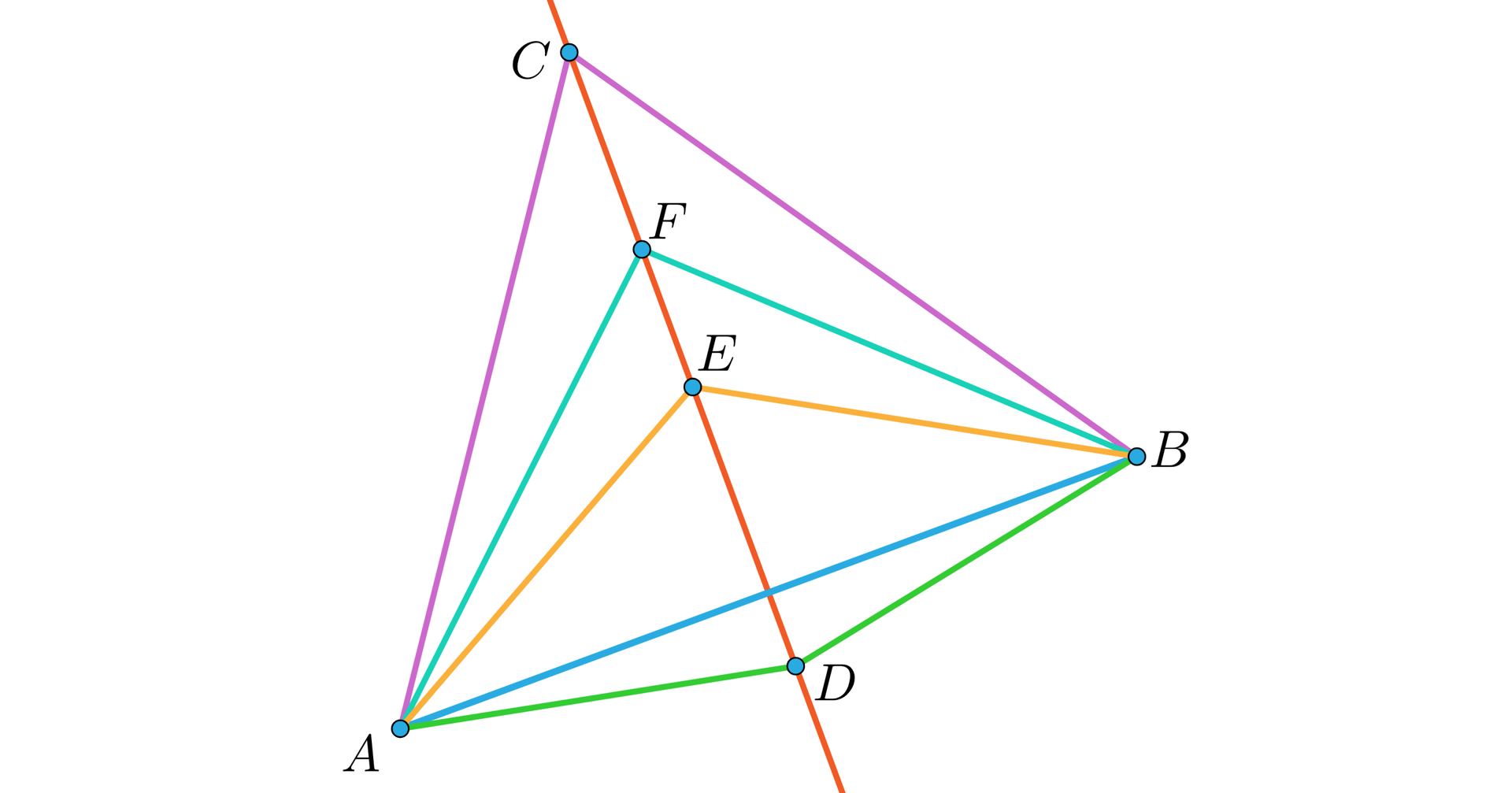
Niech dany będzie trójkąt i przez oznaczmy przecięcie symetralnych odcinka i odcinka . Wtedy, z faktu, że symetralna odcinka jest zbiorem wszystkich punktów równo odległych od jego końców wynika, że
a stąd wynika, że , czyli punkt leży również na symetralnej boku . Zatem symetralne trójkąta przecinają się w jednym punkcie.
Skonstruujemy trójkąt tak, aby narysowane proste były symetralnymi jego boków.

Rozwiązanie
Zauważmy, że istnieje nieskończenie wiele takich trójkątów. Dla dowolnego punktu na danej symetralnej (poza punktem przecięcia symetralnych) możemy wyznaczyć przykładowy bok jednego z takich trójkątów. Wybieramy dowolny punkt na jednej z symetralnych. Konstruujemy prostą prostopadłą do tej symetralnej i przechodzącą przez ten punkt. Następnie wyznaczamy dowolne punkty leżące na tej prostej równo odległe od wybranego punktu, oznaczamy je przez i .

Teraz należy skonstruować prostą prostopadłą do drugiej symetralnej przechodzącą przez jeden z końców odcinka , niech to będzie .
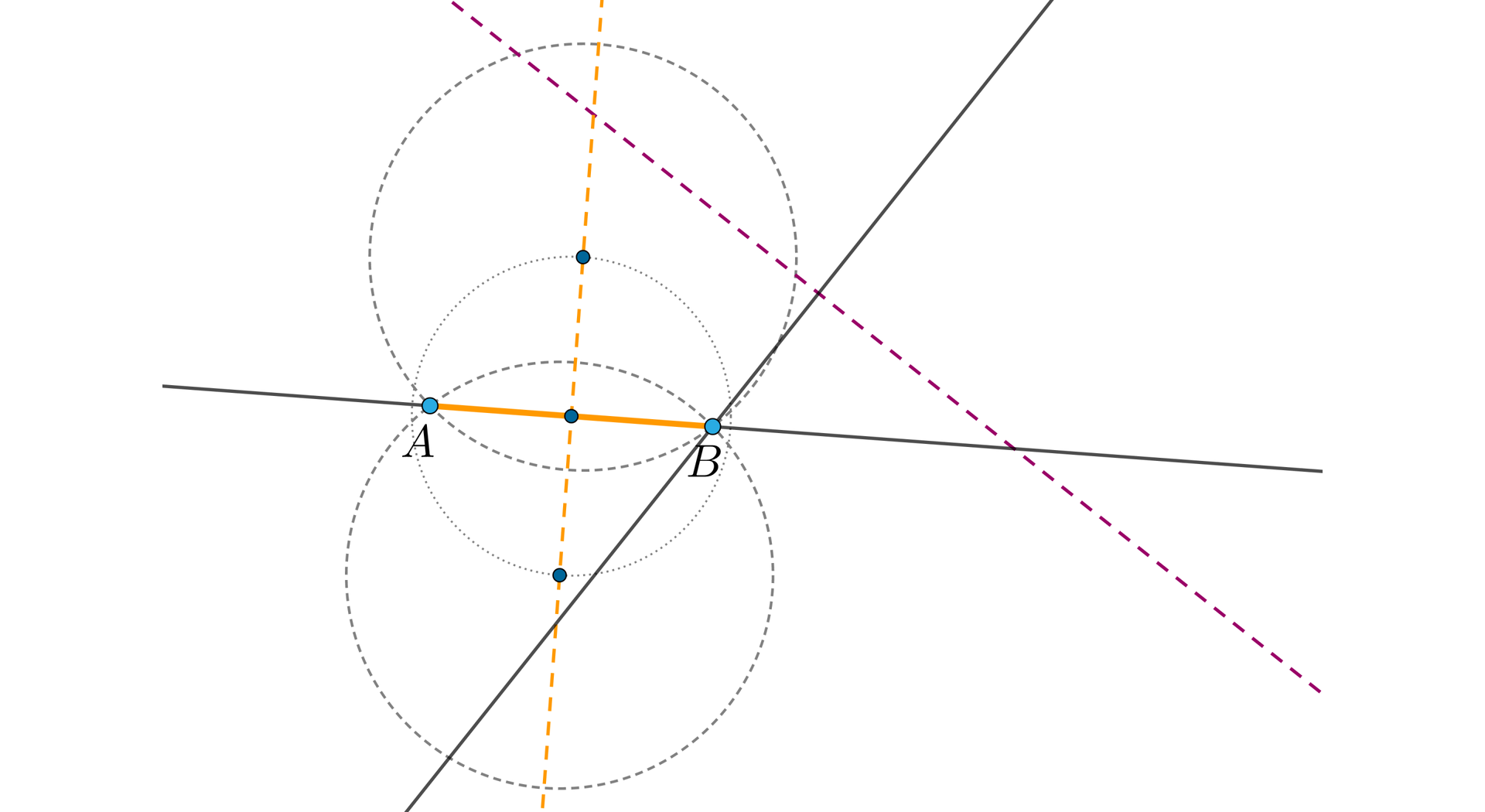
Ostatecznie musimy teraz wyznaczyć punkt leżący na tej prostej w takiej samej odległości od symetralnej co punkt .

Uzasadnienie poprawności konstrukcji
Symetralne boków trójkąta to proste, które dzielą boki trójkąta na dwie równe części i są do tych boków prostopadłe. Rzut prostokątny dowolnego punktu symetralnej na prostą zawierającą bok trójkąta będzie środkiem tego boku. Poprowadzona prosta prostopadła w tym punkcie będzie zawierać bok trójkąta. Jednak ze względu na to, że punkt wybrany na symetralnej jest środkiem tego boku to narysowany okrąg o środku w tym punkcie pozwoli nam wyznaczyć dwa wierzchołki trójkąta.
Dla danej prostej i punktu leżącego poza nią istnieje dokładnie jedna prosta prostopadła do tej prostej i przechodząca przez ten punkt. Odbicie tego punktu względem prostej wyznacza trzeci wierzchołek trójkąta.
Odległość punktu przecięcia symetralnych boków trójkąta prostokątnego równoramiennego od wierzchołka kąta prostego jest o mniejsza od długości przyprostokątnych. Obliczymy pole tego trójkąta.
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku:
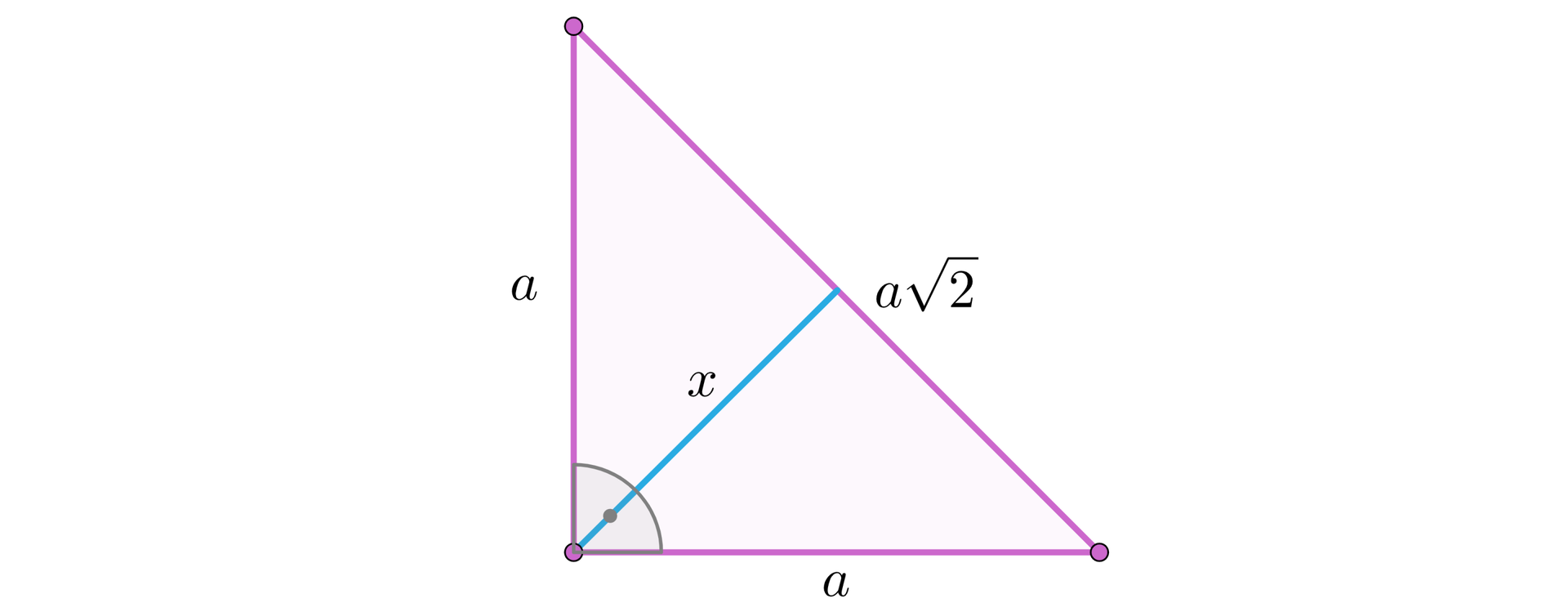
Zauważmy, że .
Zatem:
Symetralne boków ostrokątnego trójkąta równoramiennego , w którym , przecinają się w punkcie . Odległość punktu od ramion trójkąta jest równa zaś odległość punktu od wierzchołków tego trójkąta jest równa . Obliczymy obwód tego trójkąta.
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku:

Wyznaczamy długość odcinka :
Stąd: .
Wyznaczamy długość odcinka :
Stąd: , co daje: i .
Zatem: .
Obliczamy obwód trójkąta : .
Słownik
prosta, która przechodzi przez środek odcinka i jest do niego prostopadła