Problem ośmiu hetmanów – powtórzenie

Rozwiązanie problemu ośmiu hetmanów polega na znalezieniu takiego ustawienia figur hetmanów na planszy, które uniemożliwia wykonanie wzajemnego bicia.

Rzecz jest o tyle skomplikowana, że hetman, zwany również królową, ma największe wśród figur szachowych spektrum ruchów. Może on poruszać się o dowolną liczbę pól w liniach poziomych, pionowych oraz na ukos. Nie bez powodu jest to figura mająca w grze w szachy największą wartość.

R19QgZsxcqnDB

Ilustracja przedstawia białą figurę hetmana na czarnym polu na środku szachownicy. Iksami zaznaczono pola, po których figura ta może się poruszać.
Zaznaczony jest rząd pól pionowych, poziomych, oraz po skosach od pola, na którym stoi hetman. Poziom pól szachownicy oznaczony jest literami od a do h a pion od 1 do 8.

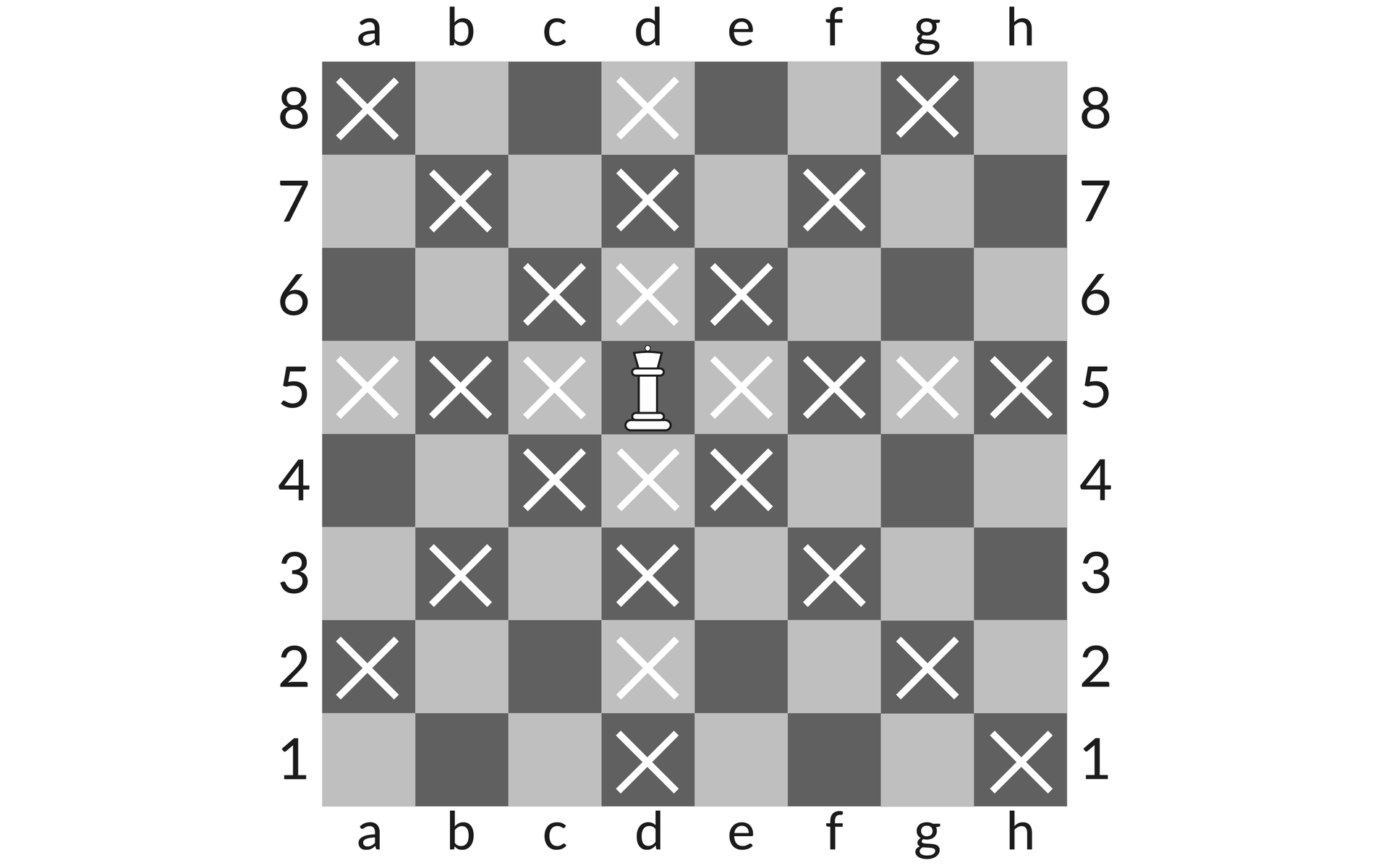
Trzeba wziąć też pod uwagę fakt, że osiem figur hetmanów musimy rozmieścić na szachownicy o wymiarach 8 x 8. Oznacza to, że przy ustawieniu spełniającym kryteria zagadki na planszy nie pozostaje ani jedno pole, które nie byłoby w zasięgu hetmanów.

Przykładowe zadanie typu maturalnego

Zadanie 1. Problem ośmiu hetmanów

Problem ośmiu hetmanów polega na takim rozstawieniu figur hetmanów na planszy, by żadna z nich nie znalazła się w pozycji, w której może zostać zaatakowana przez innego hetmana.

Rozstawienie figur zapisujemy w postaci ośmiocyfrowego ciągu liczb. Indeks danej liczby jest oznaczeniem kolumny, w której znajduje się hetman, zaś wartość liczbowa danego elementu ciągu wskazuje numer wiersza. Przykładowo, zapis (61528374) oznacza, że w kolumnie pierwszej hetman znajdzie się w szóstym wierszu, w kolumnie drugiej hetman będzie umieszczony w wierszu pierwszym itd.

R1LHLqOAG2mfP

Ilustracja przedstawia szachownicę z hetmanami ustawionymi na polach: a6, b1, c5, d2, e8, f3, g7, h4.

Hetman może poruszać się o dowolną liczbę pól w pionie i w poziomie oraz na ukos. Oznacza to, że aby rozwiązanie było prawidłowe, dla każdego hetmana muszą zostać spełnione następujące dwa warunki:

• Żaden z hetmanów nie może znaleźć się w tym samym wierszu lub kolumnie co inny.

• Żaden z hetmanów nie może znaleźć się na jednej przekątnej z innym hetmanem. Jeżeli oznaczymy pozycje dwóch hetmanów jako $(a,b)$ oraz $(x,y)$, wówczas reguła ta będzie mieć postać: $|a-x|\ne |b-y|$.

Zadanie 1.1.

Treść polecenia

W tabeli podane są przykładowe rozwiązania problemu ośmiu hetmanów. Zastanów się, które z nich są prawdziwe, a następnie wpisz odpowiednie odpowiedzi: P/F (prawda/fałsz).

Rozwiązanie zadania

Pierwszy podpunkt zadania jest dosyć prosty, a jednocześnie pozwoli oswoić się z zastosowaną notacją. Zacznijmy od interpretacji zapisu rozwiązań.

Odczytując numery wierszy z pierwszego przykładu (41584736), rozstawiamy kolejne figury na szachownicy. Zacznijmy od pierwszej liczby w ciągu. Indeks (wynoszący 1) oznacza, że pierwszego hetmana wstawimy w kolumnie pierwszej, zaś wartość liczbowa określa, że będzie to wiersz czwarty. Przyjmując zapis współrzędnych jako pary (numer kolumny, numer wiersza), pierwsza figura znajdzie się na polu (1, 4).

Pierwszego hetmana możemy ustawić na dowolnym polu, a zatem na razie nie musimy jeszcze sprawdzać żadnych warunków.

Odczytując drugą liczbę w ciągu, dowiadujemy się, że kolejna figura trafi do pierwszego wiersza drugiej kolumny, czyli (2, 1).

RY339zvjAFIex

Ilustracja przedstawia szachownicę z hetmanami ustawionymi na polach: a4, b1.

Od razu widać, że figury na pozycjach (1, 4) oraz (2, 1) spełniają pierwszy warunek niezbędny do rozwiązania problemu ośmiu hetmanów, ponieważ znajdują się w innych wierszach oraz kolumnach.

Sprawdźmy również, czy nie występuje kolizja po przekątnej. Jeżeli podstawimy pozycje hetmanów do wzoru zapisanego w zadaniu, otrzymamy wyrażenie
$|1-2|\ne |4-1|$, które potwierdza poprawność ustawienia.

Ponieważ spełnione są oba warunki niezbędne do rozwiązania problemu ośmiu hetmanów, możemy przejść do ustawiania kolejnych figur. Trudności napotkamy dopiero przy próbie uzupełnienia piątej kolumny.

RMLTEaVb9tF7c

Ilustracja przedstawia szachownicę z hetmanami ustawionymi na polach: a4, b1, c5, d8, e4.

Według zapisu hetman z piątej kolumny powinien znaleźć się w czwartym wierszu. W tym samym wierszu umieszczona została już jednak figura z pierwszej kolumny – doszło zatem do złamania pierwszego warunku opisanego w zadaniu.

Skoro mamy już pierwszą odpowiedź, przejdźmy do kolejnego przykładu. Tu również wystąpi kolizja przy wstawianiu hetmana w piątej kolumnie. Tym razem jednak nie jest ona tak łatwa do dostrzeżenia w ośmiocyfrowym zapisie ustawienia.

R1dLg9YrMrbgZ

Ilustracja przedstawia szachownicę z hetmanami ustawionymi na polach: a2, b4, c6, d8, e1.

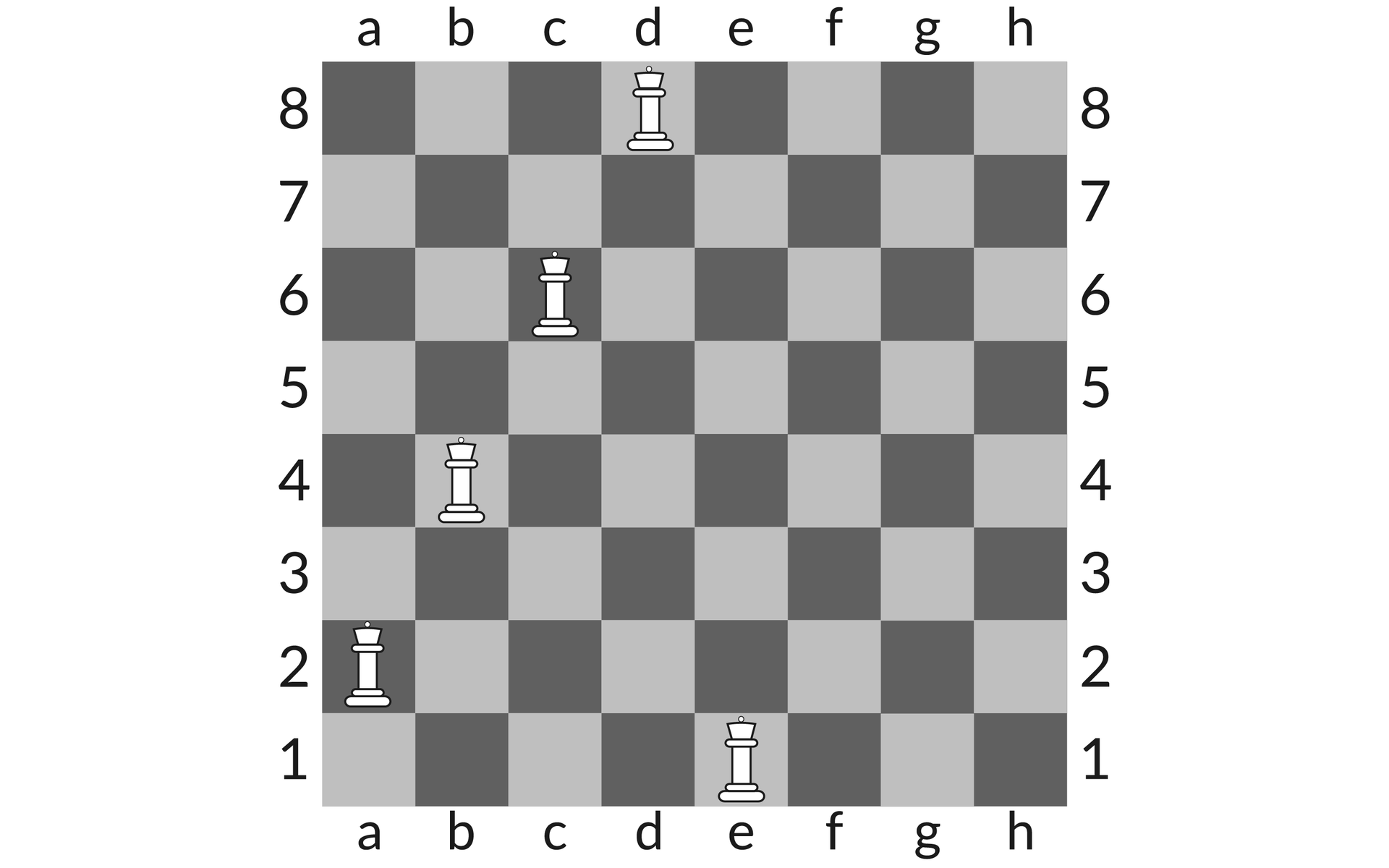
Co prawda żaden wiersz ani żadna kolumna nie zostały w tym przypadku zajęte dwa razy, jednak mamy do czynienia z kolizją przy ruchu na ukos.

Gdybyśmy chcieli wyliczyć współrzędne kolizyjne dla każdej kolejnej wpisywanej figury, z pewnością zajęłoby to dużo czasu. Najprostszym sposobem znalezienia poprawnej odpowiedzi będzie przygotowanie rysunku pomocniczego. Łatwo dostrzeżemy wówczas, na jakich pozycjach nie powinniśmy ustawiać kolejnego hetmana.

W przykładzie atakują się nawzajem figury o współrzędnych (2, 4) oraz (5, 1). Po podstawieniu tych liczb do wzoru okazuje się, że strony wyrażenia są sobie równe, a zatem mamy do czynienia z kolizją po przekątnej.

Zwróćmy uwagę na tak zwaną relację skoczkarelacja skoczkarelację skoczka – każde poprawne rozwiązanie problemu ośmiu hetmanów wymaga umieszczenia figur w układach, w których skoczek miałby możliwość bicia.

Jeżeli dla kolejnych dwóch przykładów sprawdzisz warunki przedstawione w treści zadania (bądź wykonasz odpowiednie rysunki), przekonasz się, że są to poprawne rozwiązania problemu ośmiu hetmanów.

Poprawna odpowiedź

Zadanie 1.2.

Treść polecenia

Prześledź algorytm z nawrotamialgorytm z nawrotamialgorytm z nawrotami opisany w postaci listy kroków i ustal, jakie pozycje figur na planszy będą skutkowały wywołaniem nawrotu. Do nawrotu dochodzi w momencie, gdy figury znajdą się w pozycji prowadzącej do wzajemnego bicia.

Jeżeli odkryjesz, że wstawienie hetmana bądź zmiana jego pozycji w danej kolumnie nie są możliwe, zasygnalizuj to, wpisując „X” w miejscu wiersza niemożliwego do obsadzenia.

Wywołanie wykonaj dla początkowego układu: (60000000). Jeżeli uzupełnienie wiersza tabeli jest niemożliwe, ponieważ nawrót o numerze n nie zachodzi – zasygnalizuj to, wpisując notę: „nie dotyczy” zamiast kombinacji wywołującej nawrót.

RQhmDY1bqe1A6

Ilustracja przedstawia szachownicę z hetmanem ustawionym na polu: a6.

Lista kroków:

1. Wybieramy wiersz początkowy, który znajdzie się na pierwszej pozycji ciągu. Możemy wybrać liczby z przedziału <1, 8>.

2. Jeżeli wszystkie hetmany zostały ustawione, wypisujemy rozwiązanie.

3. Szukamy wolnego wiersza dla następnej kolumny, która nie jest jeszcze obsadzona. Dobieramy kolejne liczby, zaczynając od wiersza pierwszego, a kończąc na wierszu ósmym.

4. Jeżeli znaleźliśmy takie pole, sprawdzamy, czy nie dochodzi na nim do bicia z figurami stojącymi już na planszy.

5. Jeżeli nie znaleźliśmy takiego pola, które jest poza zasięgiem ruchu ustawionych już figur, zdejmujemy hetmana z poprzedniej kolumny i wracamy do kroku trzeciego.

6. Jeżeli znaleźliśmy pole nieatakowane przez inną figurę, ustawiamy na nim hetmana, a następnie powracamy do kroku drugiego.

Przykład:

Sprawdźmy rezultat zastosowania algorytmu z zajętym początkowo czwartym wierszem pierwszej kolumny równym 4. Rozpatrujemy zatem układ (40000000).

Drugi krok nie jest spełniony dopóty, dopóki nie wyeliminujemy wszystkich zer z ośmiocyfrowego ciągu. W trzecim kroku szukamy pierwszego od lewej strony zera w rozwiązaniu. Znajdziemy je na drugiej pozycji, więc w tym przebiegu obsadzimy drugą kolumnę.

Ponieważ jest to dopiero druga figura do wstawienia, wiele pól pozostało jeszcze wolnych. Umieśćmy więc hetmana z drugiej kolumny w pierwszym wierszu. W rezultacie układ będzie miał postać (41000000). Wykonując krok czwarty, sprawdzamy, czy nie występuje żadna kolizja.

Do wzajemnego atakowania się figur nie doszło, a zatem pomijamy krok piąty i przechodzimy do szóstego: ustawiamy hetmana w znalezionym polu i wracamy do kroku drugiego.

Opisane czynności powtarzamy aż do momentu wystąpienia ewentualnej kolizji (czyli sytuacji, w której dwa hetmany się atakują). W takim przypadku będziemy musieli dokonać nawrotu: zdjąć ostatniego obsadzonego hetmana i spróbować ustawić go na innej pozycji. Jeżeli takiego miejsca nie znajdziemy, ponownie dokonamy nawrotu, czyli zdejmiemy poprzedniego hetmana itd.

Rozwiązanie

Przedstawione zadanie jest typowym ćwiczeniem polegającym na analizowaniu algorytmu. Wykonujemy kolejne czynności, aby zrozumieć ideę algorytmu oraz przyswoić sobie mechanizm nawrotów. Będziemy obserwować na bieżąco skutek jego zastosowania.

Pierwsze ustawienie jest z góry narzucone, więc od razu zaczynamy od poszukiwania wolnego wiersza w drugiej kolumnie. Do dyspozycji mamy już pierwszy wiersz, więc ośmiocyfrowy ciąg przybierze postać: (61000000).

Dla każdej kolumny poszukujemy rozwiązania (wolnego pola), zaczynając od pierwszego wiersza, a kończąc na ósmym. Kierując się taką właśnie, przyjętą odgórnie zasadą, nie przeoczymy żadnej kombinacji, która mogłaby spełniać warunki zadania.

W trzeciej kolumnie pierwszym bezkolizyjnym wierszem jest wiersz trzeci. W kolumnach od czwartej do siódmej wolne są (odpowiednio): wiersz piąty, siódmy, drugi oraz czwarty. Mamy więc do czynienia z następującym układem: (61357240).

R26lSh6ZEvTob

Ilustracja przedstawia szachownicę z hetmanami ustawionymi na polach: a6, b1, c3, d5, e7, f2, g4.

W ósmej kolumnie hetmana możemy wstawić jedynie w wierszu ósmym, jednak atakuje go hetman ustawiony na pozycji (3, 3). Jest to zatem pierwszy nawrót; układem wywołującym go jest (6135724X). Taki sam zapis znajdziemy w uzupełnionej już części tabelki, co potwierdza poprawność takiego rozumowania.

Ponieważ doszło do nawrotu, zdejmujemy hetmana z siódmej kolumny  i szukamy dla niego innego miejsca na szachownicy. Wędrując po kolejnych wierszach, stwierdzamy, że moglibyśmy go wstawić jedynie w wierszu ósmym. W tym przypadku wystąpi jednak kolizja z hetmanem na pozycji (4, 5). Ponieważ nie jest możliwe wstawienie figury w żadnym innym miejscu, notujemy, iż układem wywołującym nawrót jest (613572X0).

Przekładamy zatem hetmana z szóstej kolumny z drugiego wiersza. Szukając dla niego miejsca, widzimy, że wolne są wiersze czwarty i ósmy. Przekładamy zatem hetmana z wiersza drugiego na wiersz czwarty. Nie dochodzi do żadnego ataku między nim a innymi hetmanami. Możemy przejść do kolejnej — siódmej kolumny.

W tym momencie hetmana możemy spróbować ustawić w wierszu drugim oraz wierszu ósmym. W obu przypadkach jednak nie będzie to możliwe ze względu na atak hetmana z kolumny czwartej. Następuje powrót. Kombinacja, którą wpisujemy do tabeli to (613574X0).

Hetman z szóstej kolumny był już przełożony, zatem kolejnym wierszem, który sprawdzamy, jest wiersz ósmy, jednak jest to pole atakowane przez hetmana z kolumny piątej. Próba znalezienia miejsca zakończyła się fiaskiem i skutkuje kolejnym nawrotem w układzie (61357X00).

Poszukiwanie kontynuujemy, przestawiając hetmana w piątej kolumnie z wiersza siódmego do wiersza ósmego. Przechodzimy do kolumny szóstej. W tym momencie wolne wiersze to drugi, czwarty i siódmy. W przypadku dwóch pierwszych są to pozycje, które nie są atakowane. Kontynuujemy, ustawiając hetmana w wierszu drugim. Następną kolumną, którą chcemy obsadzić, jest kolumna siódma. Wolne wiersze to wiersz czwarty oraz siódmy. Pozycja w wierszu czwartym jest odpowiednia, zatem ustawiamy tu hetmana. Przechodzimy do ostatniej kolumny. Niestety okazuje się, że ostatni wolny wiersz — siódmy, jest atakowany. Następuje powrót. Wpisujemy do tabeli (6135824X). Ponieważ wiersz siódmy jest również atakowany na kolumnie siódmej, następuje kolejny powrót – kombinacja (613582X0).

Wytłumaczyliśmy, w jaki sposób szukać kolejnych kombinacji wykonujących powrót. W podobny sposób dojdziemy do kolejnych rozwiązań, które prezentują się następująco:

• (613584X0)

• (61358X00)

• (6135X000)

• (6137X000)

W tym momencie wypełnimy już całą tabelę, więc możemy przestać podążać za algorytmem.

Warto zaznaczyć, że dalsze podążanie opisanym algorytmem doprowadzi nas jeszcze do dwóch powrotów — kombinacji (6138X000) oraz (613X0000), a następnie do kombinacji (61528374), która jest poprawnym rozwiązaniem problemu ośmiu hetmanów.

Warto zwrócić uwagę na to, że problem, który jeszcze chwilę temu zdawał się ogromnym wyzwaniem, przy doborze odpowiedniego algorytmu jest możliwy do rozwiązania bez wykorzystania komputera. Problem ośmiu hetmanów doskonale obrazuje, na czym polega stosowanie algorytmów z nawrotami.

Poprawna odpowiedź

Słownik