Przeczytaj
Podstawową jednostką miary pola jest metr kwadratowy.
Inne, stosowane w praktyce jednostki miary pola to:
milimetr kwadratowy: ,
centymetr kwadratowy: ,
decymetr kwadratowy: .
Pole powierzchni gruntu podaje się często w:
arach – jest równy polu kwadratu o boku ,
hektarach – jest równy polu kwadratu o boku ,
kilometrach kwadratowych – jest równy polu kwadratu o boku .
W zadaniach dotyczących pól będziemy stosowali następujące zasady:
figura, którą można podzielić na dwie figury o polach odpowiednio oraz , ma pole ,
jeśli pewna figura ma pole , a druga jest do niej przystająca, to ta druga figura też ma pole .
Na początku przypomnimy wzór na pole prostokąta.
Pole prostokąta
Pole prostokąta o bokach oraz jest równe .
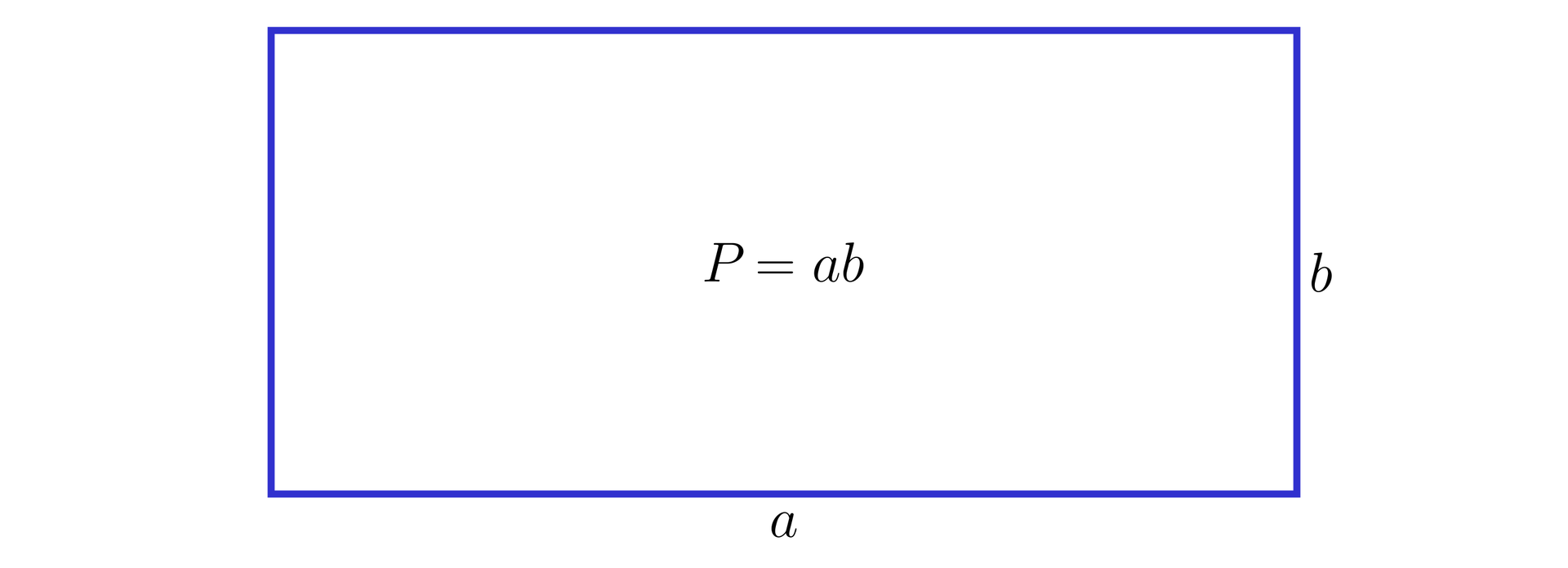
Korzystając ze wzoru na pole prostokąta, możemy wyznaczać pola innych figur.
Pole trójkąta
Pole trójkąta o wysokości opuszczonej na bok długości jest równe:
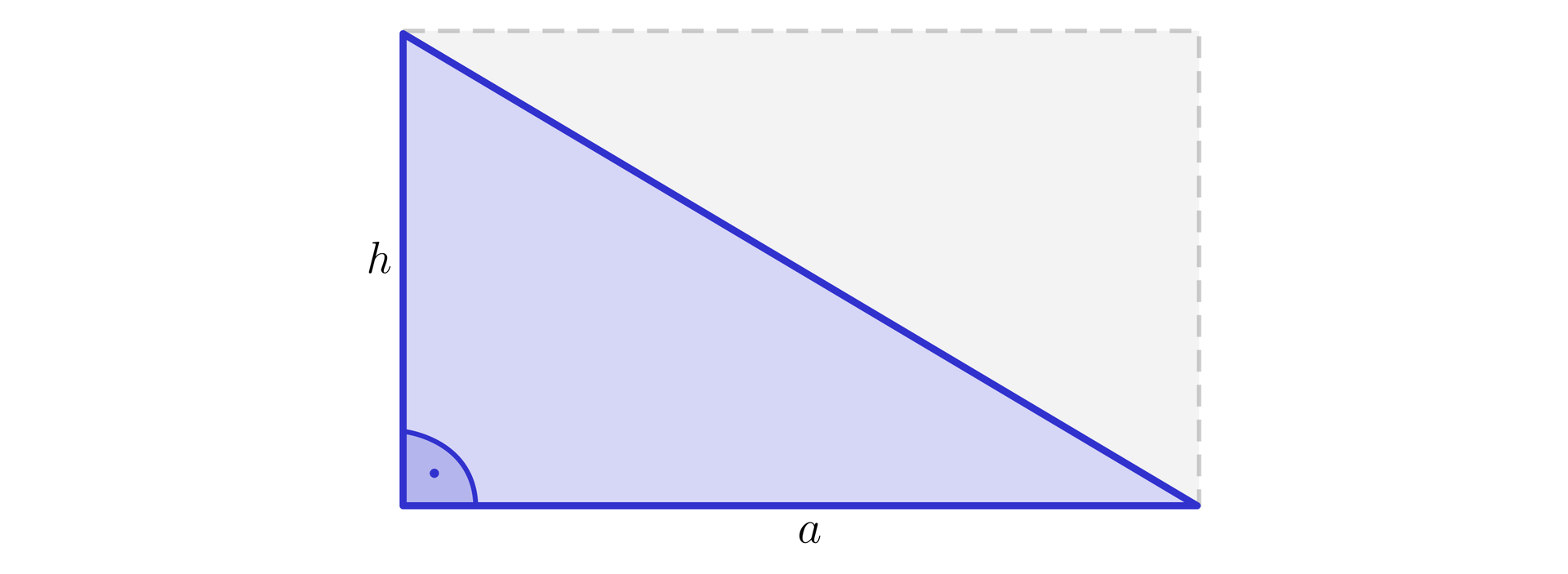
Jeśli trójkąt jest prostokątny, to jego pole stanowi połowę pola prostokąta o bokach i . Zatem jest równe .
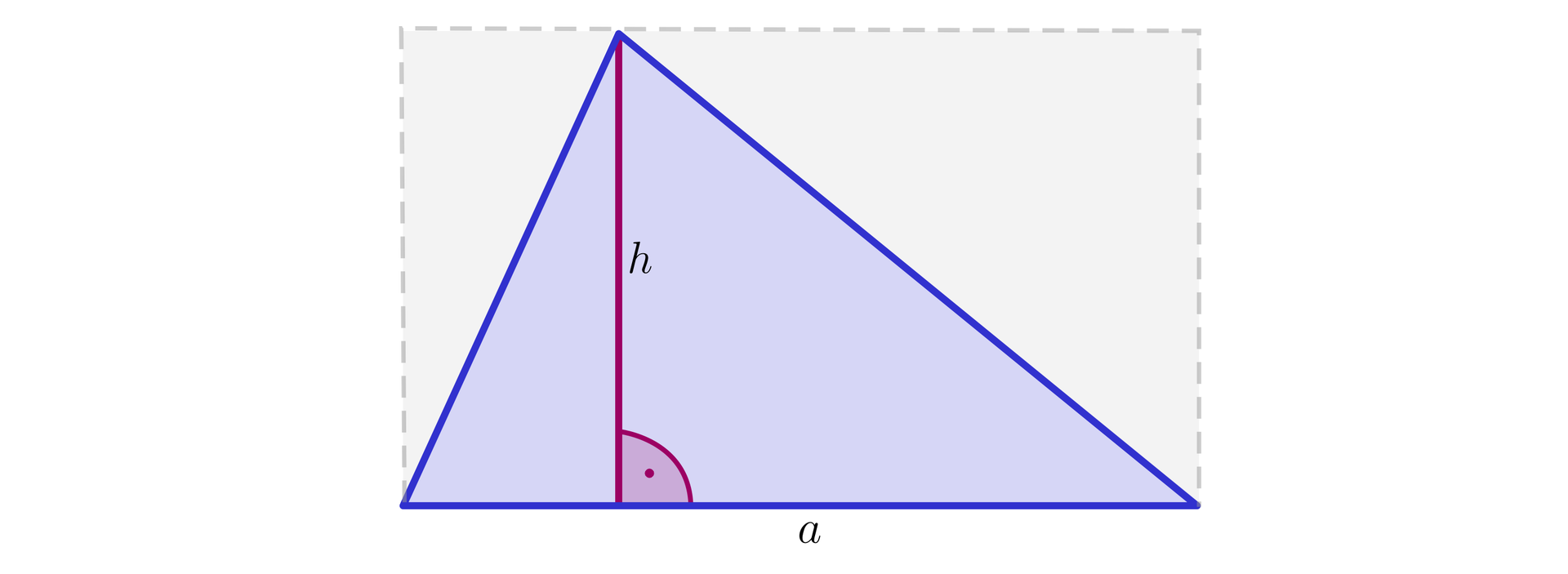
Gdy wysokość łączy wierzchołek trójkąta z przeciwległym bokiem, to pole trójkąta też jest połową pola prostokąta o bokach i (patrz rysunek).
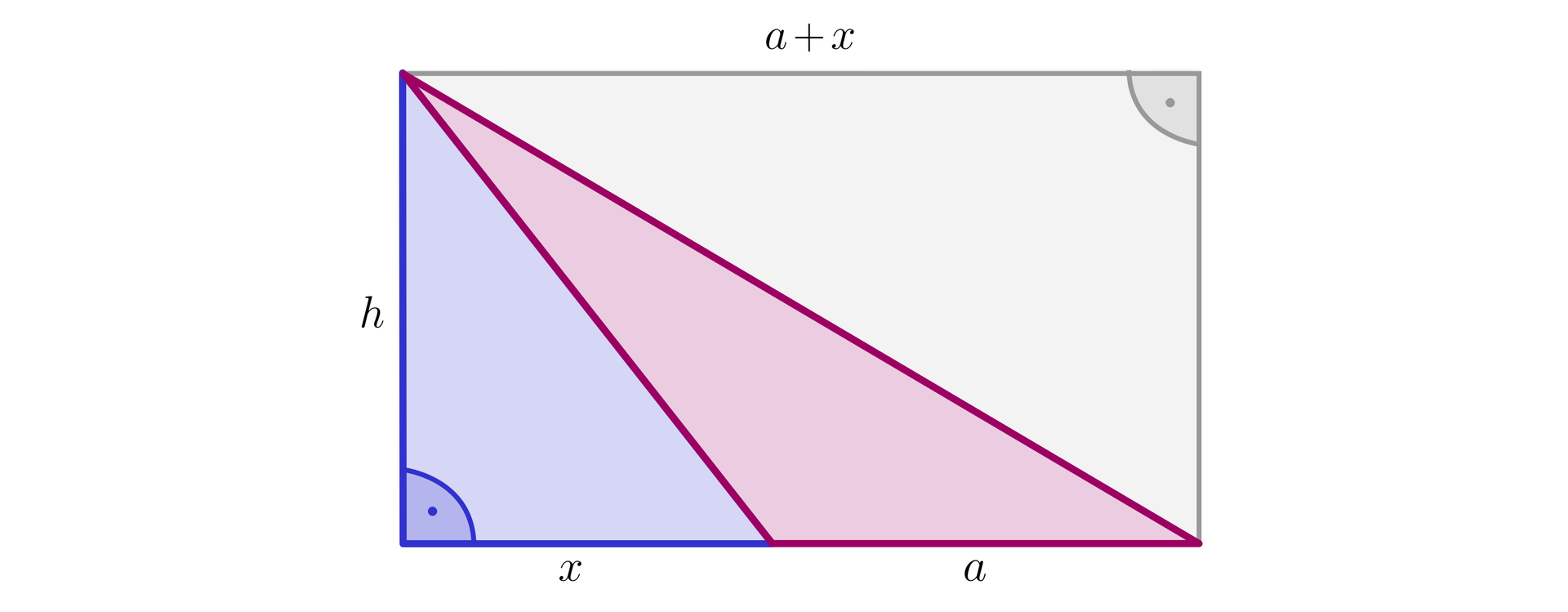
Jeśli wysokość łączy wierzchołek trójkąta z przedłużeniem przeciwległego boku to, aby wykazać prawdziwość wzoru , wprowadzimy oznaczenia, jak na poniższym rysunku. Pola dwóch kolorowych trójkątów dają w sumie połowę pola prostokąta o bokach oraz . Z tego, co już wykazaliśmy, pole niebieskiego trójkąta prostokątnego wynosi , zatem pole różowego trójkąta jest równe:
Słowa „wysokość” używać będziemy w dwóch znaczeniach. W zależności od kontekstu będzie chodziło o odpowiedni odcinek lub o jego długość.
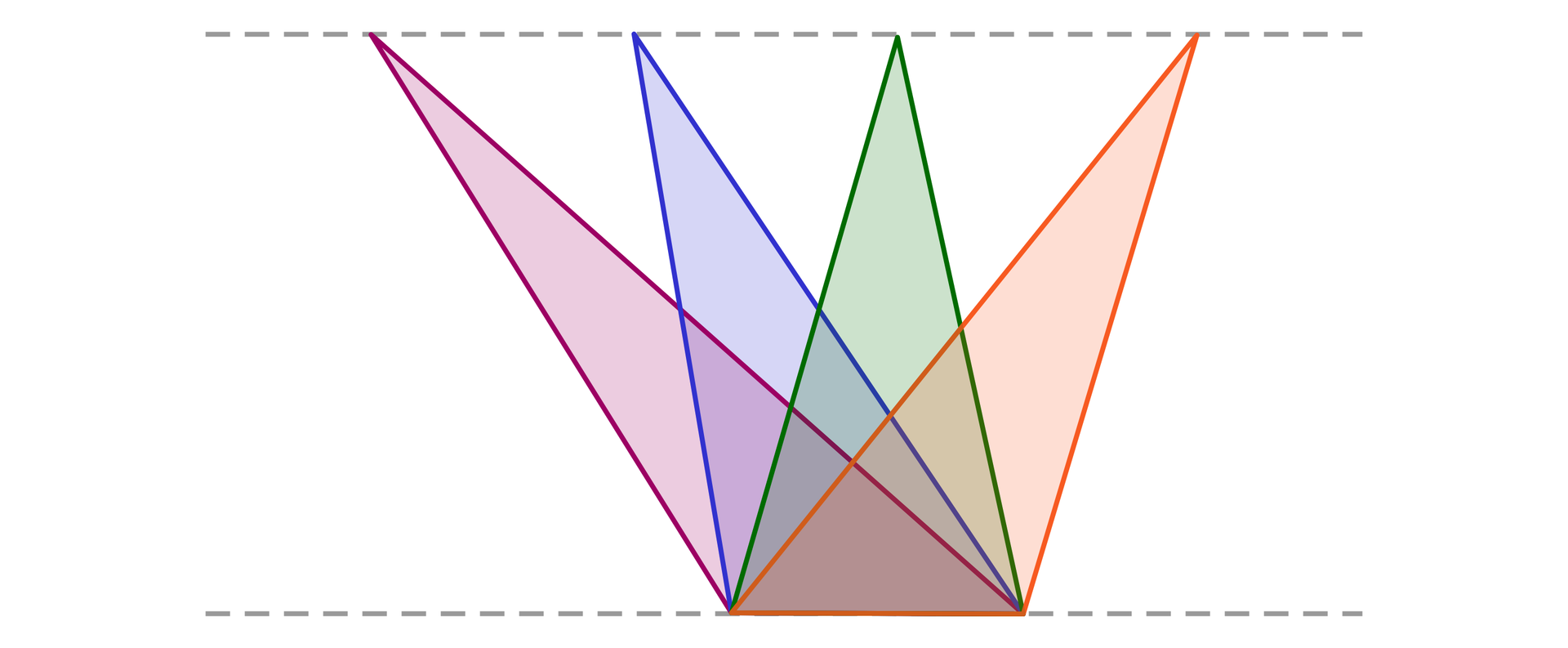
Na poniższym rysunku proste zaznaczone linią przerywaną są równoległe. Wszystkie kolorowe trójkąty mają więc równe pola, gdyż mają wspólny bok (podstawę) i równej długości wysokości opuszczone na prostą zawierającą ten bok. Wynika stąd, że przy ustalonym polu, obwód trójkąta może być dowolnie duży.
Pole równoległoboku
Pole równoległoboku jest równe
gdzie jest dowolnym bokiem równoległoboku, a jest wysokością opuszczoną na ten bok.
Skorzystajmy z rozumowania dotyczącego pola trójkątów.
Pole równoległoboku o boku długości i odpowiadającej mu wysokości jest równe: , ponieważ jest sumą pól dwóch przystających trójkątów, o polu każdy.

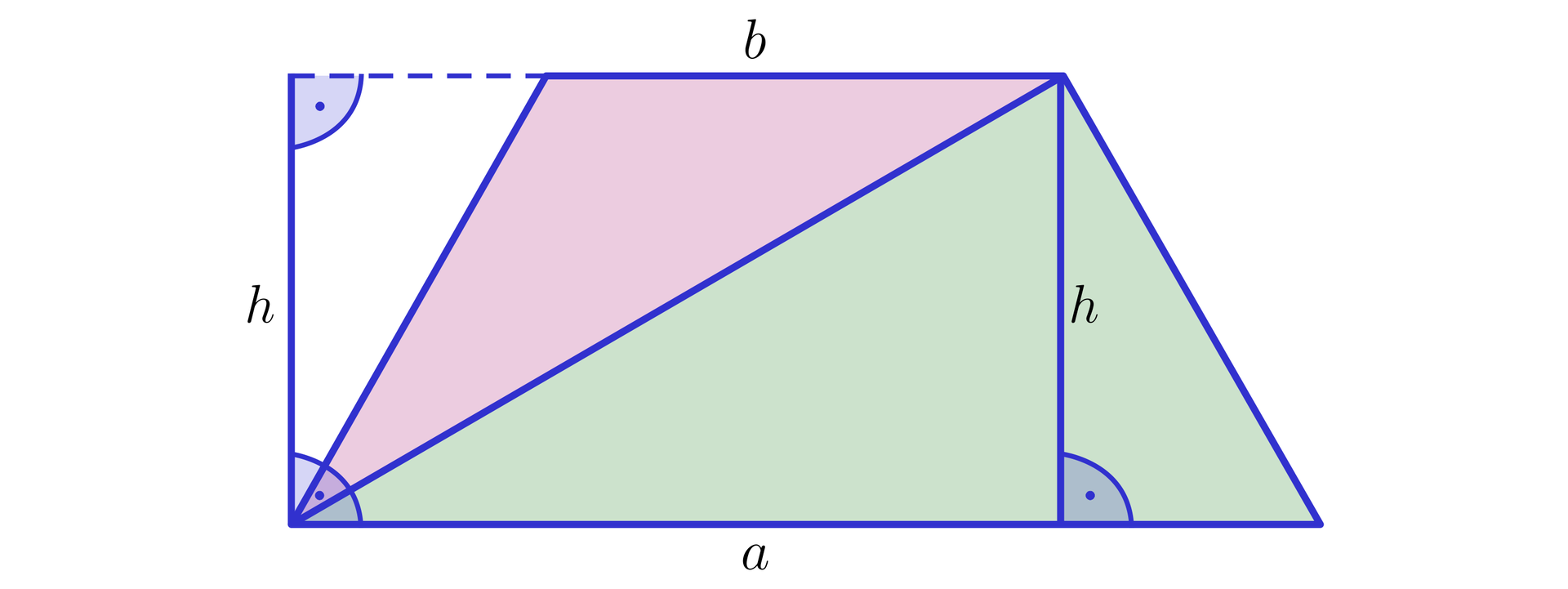
Pole trapezu o podstawach długości , i wysokości jest równe
Pole trapezutrapezu o podstawach i oraz o wysokości jest równe: , gdyż jest sumą pól dwóch trójkątów o polach odpowiednio i .
Pole dowolnego wielokąta
Pole dowolnego wielokąta obliczamy zwykle w ten sposób, że dzielimy go na trójkąty i dodajemy pola wszystkich trójkątów otrzymanych w wyniku tego podziału.
Przypomnijmy teraz najbardziej znane twierdzenie geometrii elementarnej.
Jeżeli w trójkącie prostokątnym przyprostokątne mają długości oraz , a długość przeciwprostokątnej jest równa , to:

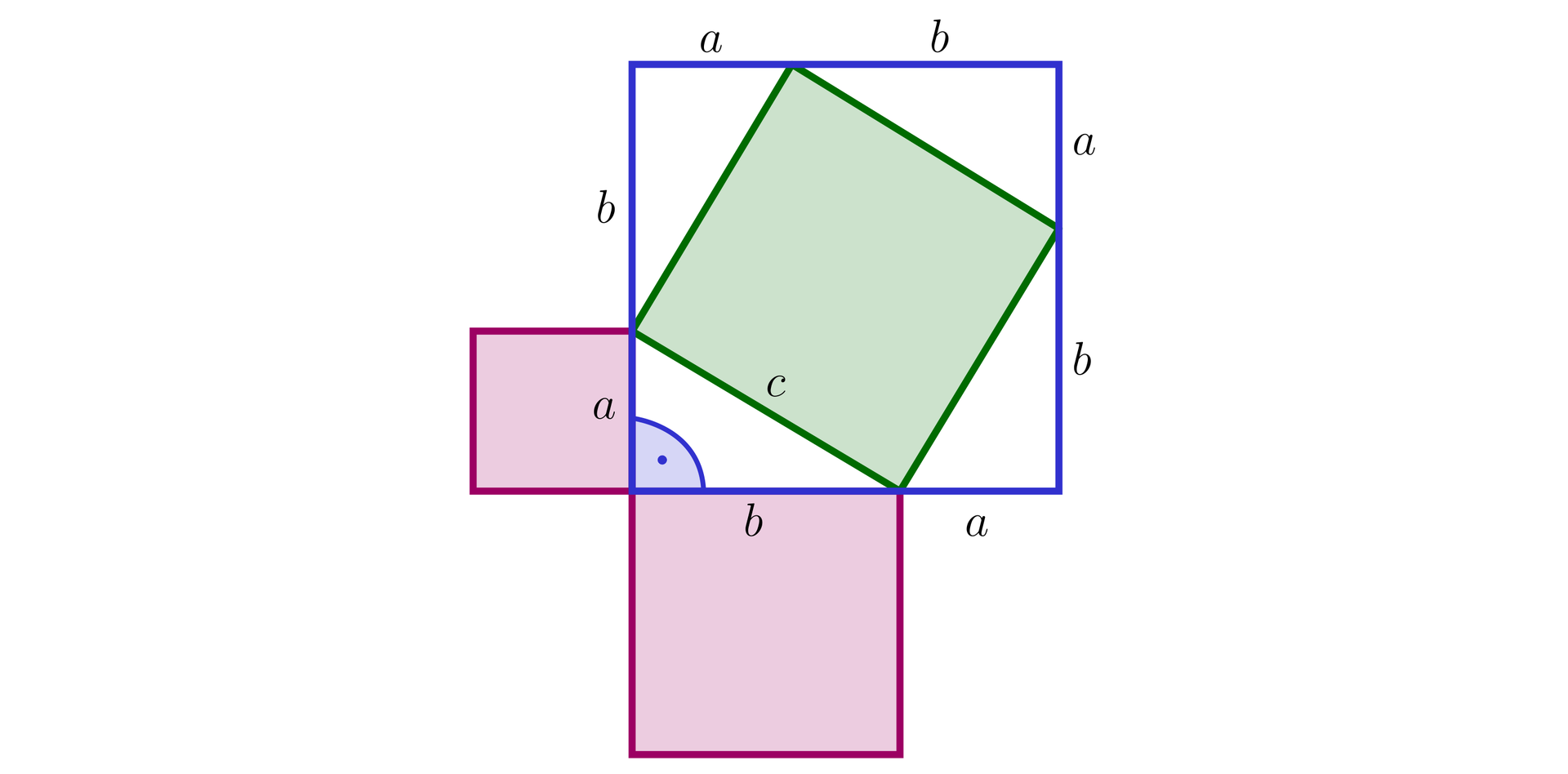
Na rysunku poniżej przedstawiono kwadrat o boku . Pole zielonego kwadratu jest równe (gdyż jest on zbudowany na przeciwprostokątnej długości ). Z drugiej strony jest ono równe różnicy pól dużego kwadratu i pól czterech małych, przystających trójkątów. Stąd:
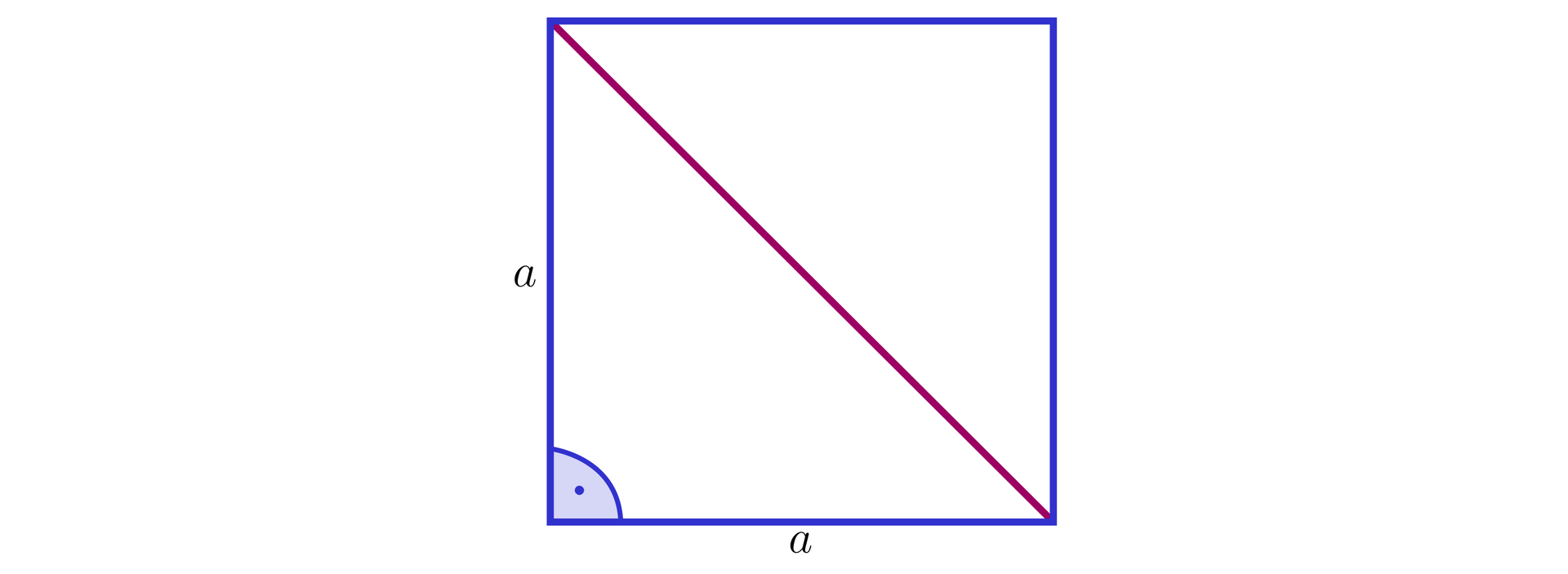
Przekątna kwadratu o boku ma zgodnie z twierdzeniem Pitagorasa długość: .
Zachodzi też twierdzenie odwrotne do twierdzenia Pitagorasa, które brzmi następująco: Jeśli w trójkącie o bokach długości , oraz zachodzi równość , to jest on prostokątny, zaś jest jego przeciwprostokątną.
a) Trójkąt o bokach: , i jest prostokątny, ponieważ: .
b) RównoległobokRównoległobok, którego przekątne mają długości i , a jeden z boków ma długość nie jest rombem (jego przekątne nie są prostopadłe).
Zauważmy mianowicie, że jeden z trójkątów otrzymanych z podziału tego równoległoboku przekątnymi ma boki o długościach , i . Przekątne w rombie przecinają się pod kątem prostym, zatem możemy skorzystać z twierdzenia Pitagorasa. Ponieważ oraz , więc , czyli ten trójkąt nie jest prostokątny. Oznacza to, że rozpatrywany równoległobok nie jest rombem.
Wysokość w trójkącie równobocznym o boku ma długość:
Korzystając z twierdzenia Pitagorasa, przy oznaczeniach jak na rysunku poniżej mamy:

W konsekwencji pole trójkąta równobocznego o boku jest równe:
Wykażemy, że jeżeli punkt leży na boku trójkąta , to stosunek pola trójkąta do pola trójkąta jest równy .
Dowód
Oznaczmy przez wysokość trójkąta opuszczoną z wierzchołka na bok (zobacz rysunek poniżej).
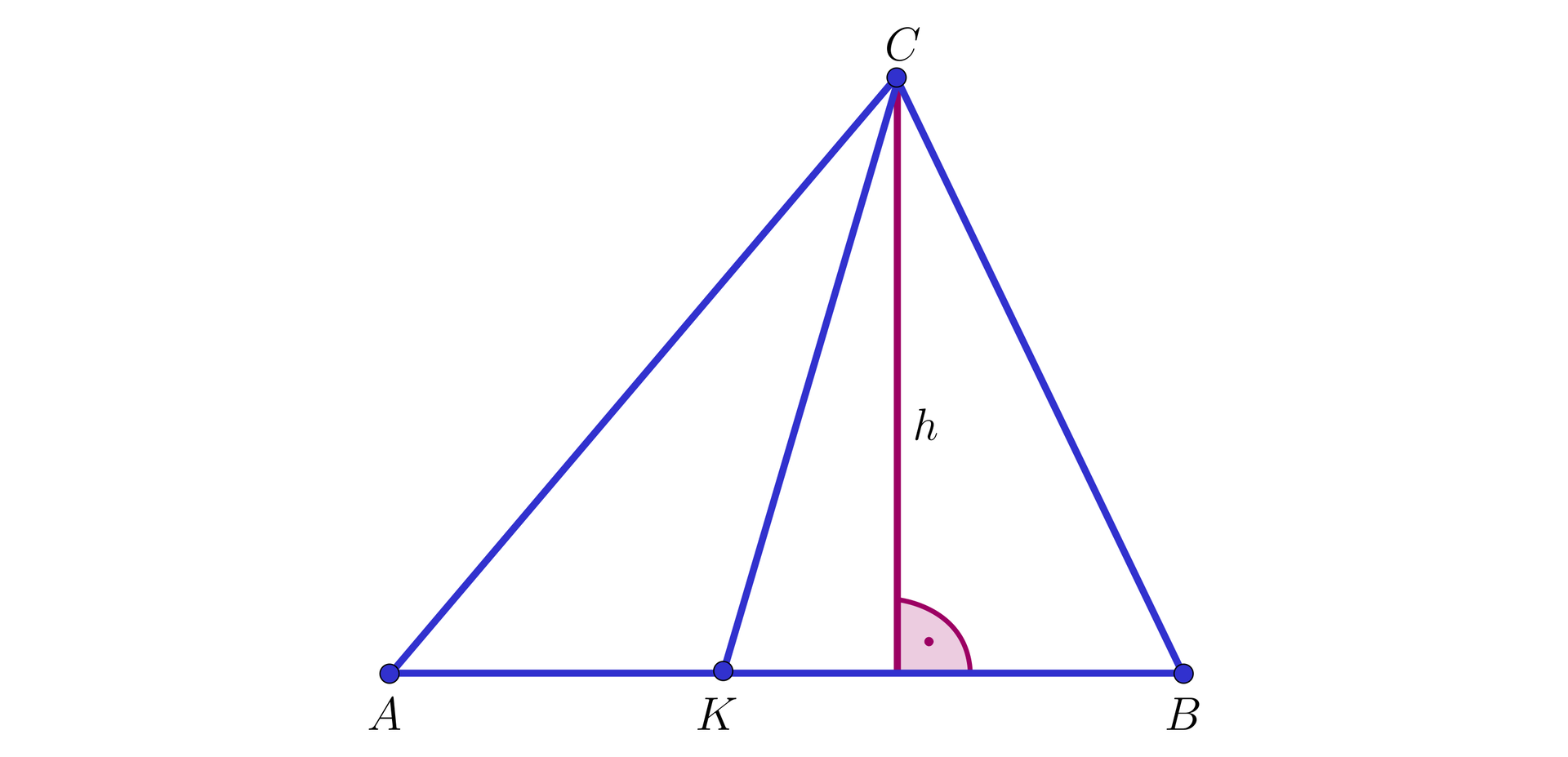
Wówczas pola trójkątów oraz możemy wyrazić za pomocą i długości odpowiedniej podstawy:
,
.
Wynika stąd, że
,
a to właśnie mieliśmy udowodnić.
Uwaga
W szczególności wynika stąd, że punkt jest środkiem boku wtedy i tylko wtedy, gdy pola trójkątów oraz są równe.
Wewnątrz trójkąta leży punkt . Proste i przecinają się w punkcie (zobacz rysunek poniżej).
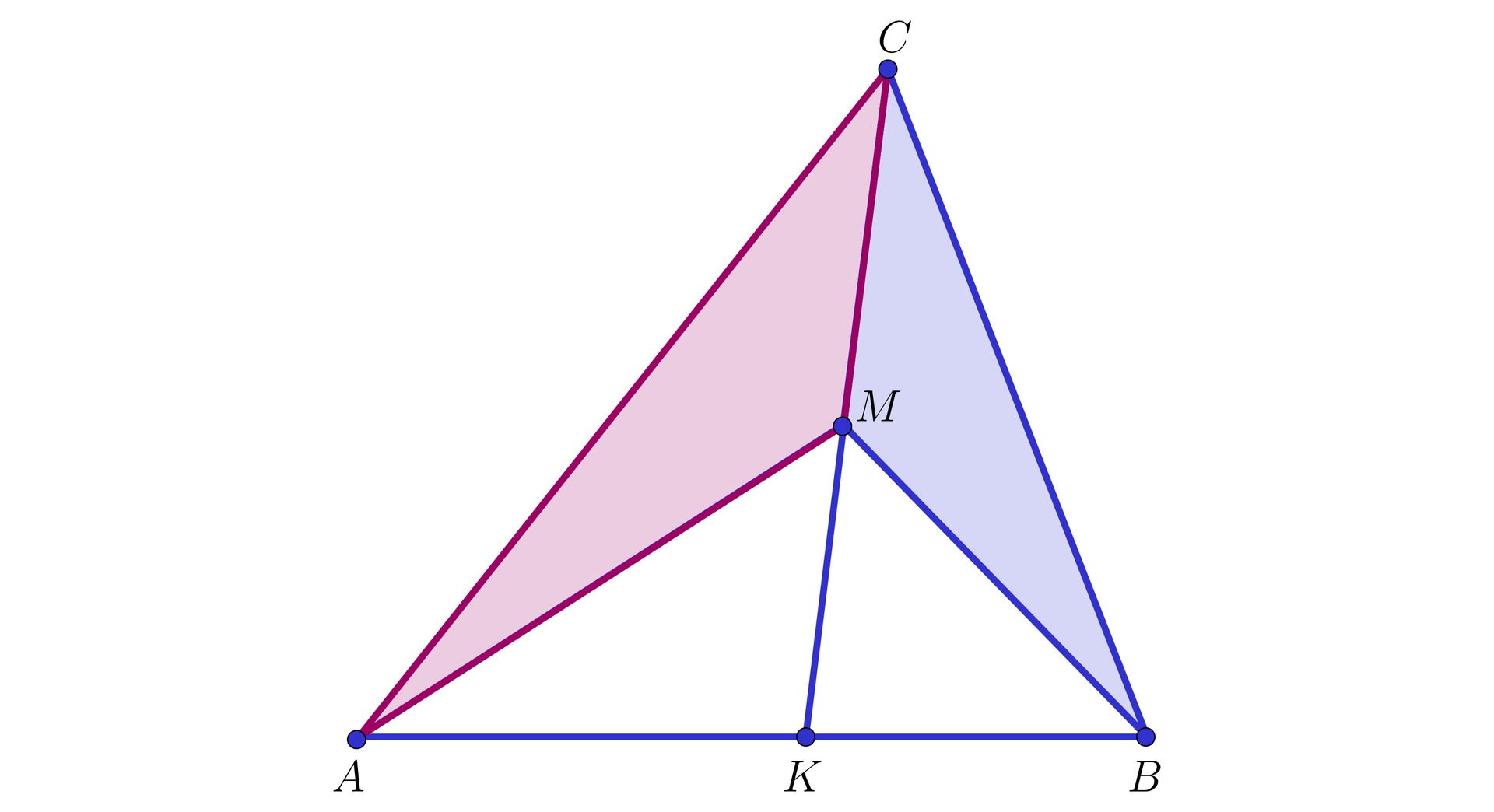
Wykażemy, że stosunek pola trójkąta do pola trójkąta jest równy stosunkowi odcinków do :
.
Dowód
Zauważmy, że:
ponieważ punkt leży na boku trójkąta , więc stosunek pola trójkąta do pola trójkąta jest równy (patrz poprzedni przykład).
Wynika stąd, że .
ponieważ punkt leży na boku trójkąta , więc stosunek pola trójkąta do pola trójkąta jest równy .
Oznacza to, że .
ponieważ pole trójkąta jest równe sumie pól trójkątów i , a także pole trójkąta jest równe sumie pól trójkątów i , więc
.
Stąd .
Wykażemy że środkowe trójkąta dzielą go na sześć części o równych polach.
Dowód
Rozpatrzmy trójkąt , w którym środki boków , oraz oznaczamy przez - odpowiednio - , i , a punkt przecięcia środkowych (czyli środek ciężkości trójkąta ) oznaczamy przez (zobacz rysunek poniżej).
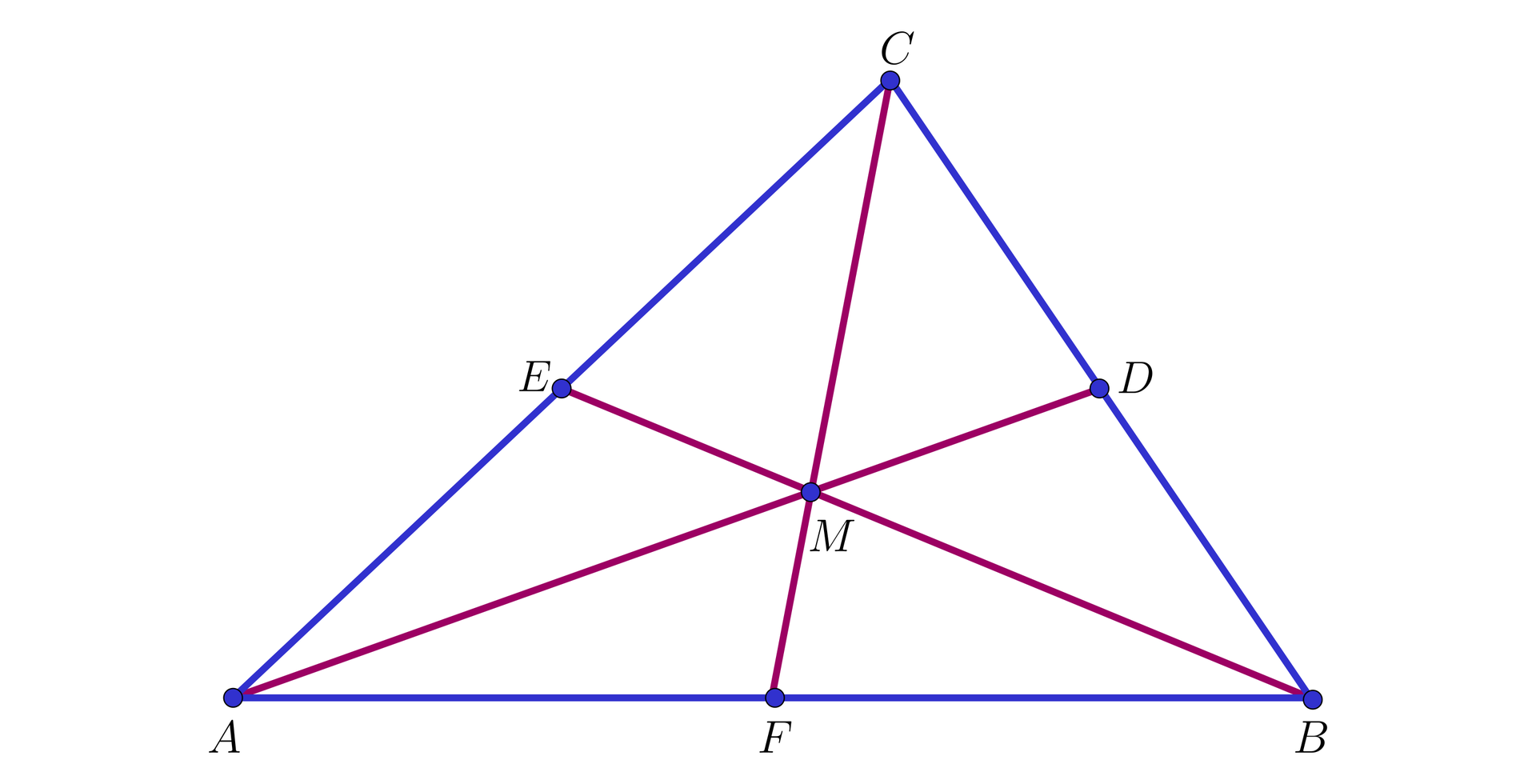
Zauważmy, że:
ponieważ punkt jest środkiem boku trójkąta , więc pola trójkątów oraz są równe . Oznaczamy każde z tych pól przez . Wtedy pole trójkąta jest równe ;
ponieważ punkt jest środkiem boku trójkąta , więc pola trójkątów oraz są równe. Oznaczamy każde z tych pól przez . Wtedy pole trójkąta jest równe ;
ponieważ punkt jest środkiem boku trójkąta , więc pola trójkątów oraz są równe. Oznaczamy każde z tych pól przez . Wtedy pole trójkąta jest równe .
Ponadto zauważmy, że:
ponieważ prosta przecina bok trójkąta w środku tego boku, więc pola trójkątów oraz są równe (patrz poprzednie przykłady). Zatem , skąd ;
ponieważ prosta przecina bok trójkąta w środku tego boku, więc pola trójkątów oraz są równe. Zatem , skąd .
Wobec tego , co oznacza, że
.
Wynika stąd, że w dowolnym trójkącie trzy środkowe boków dzielą ten trójkąt na sześć trójkątów o równych polach.
Udowodnimy, że jeżeli przekątne czworokąta wypukłego przecinają się w punkcie (zobacz rysunek), to pola trójkątów: , , oraz spełniają warunek
.
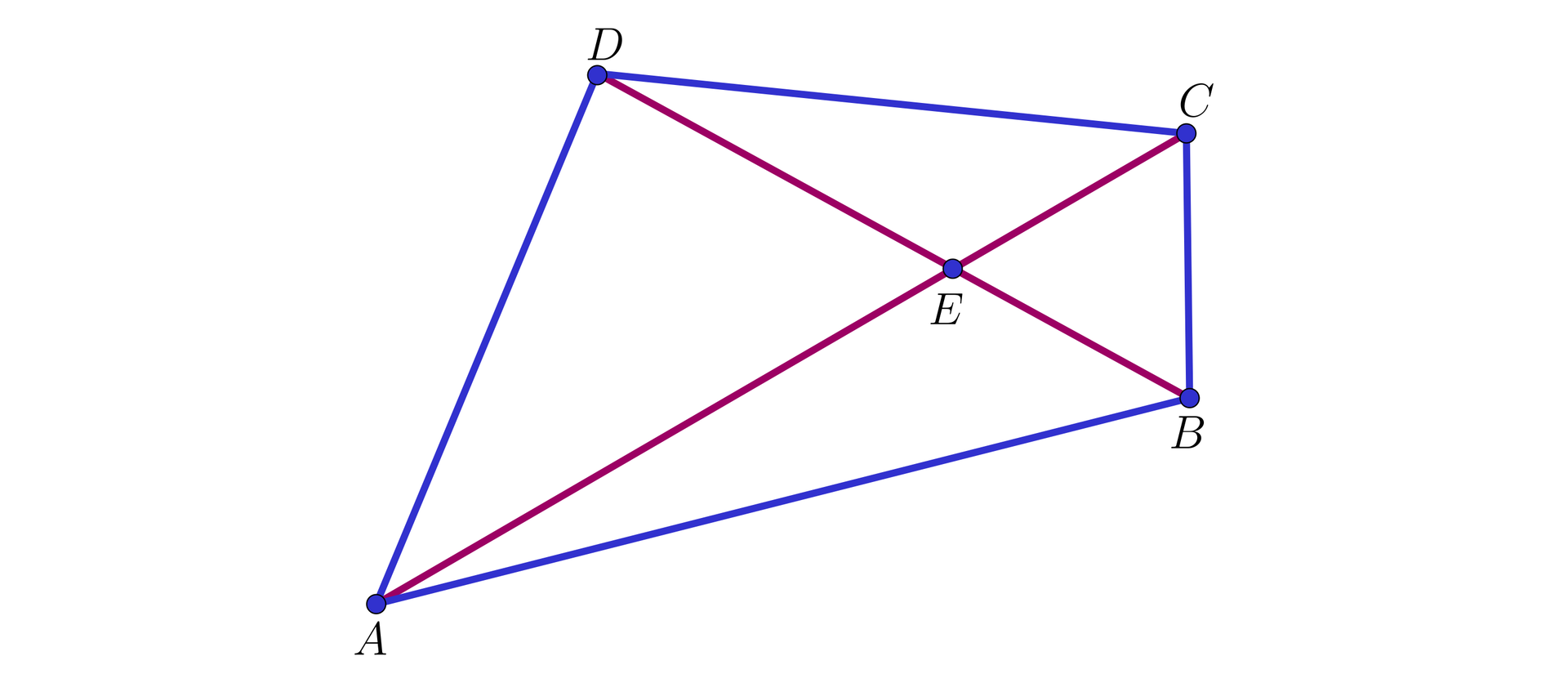
Dowód
Skorzystamy z wniosku udowodnionego w przykładzie .
Ponieważ:
punkt leży na boku trójkąta , więc ,
punkt leży na boku trójkąta , więc .
Wynika stąd, że , a więc .
To spostrzeżenie kończy dowód.
W trapezie równoramiennym o podstawach i przekątne i przecinają się w takim punkcie , że . Pole trójkąta jest równe . Oblicz pole trapezu .
Rozwiązanie
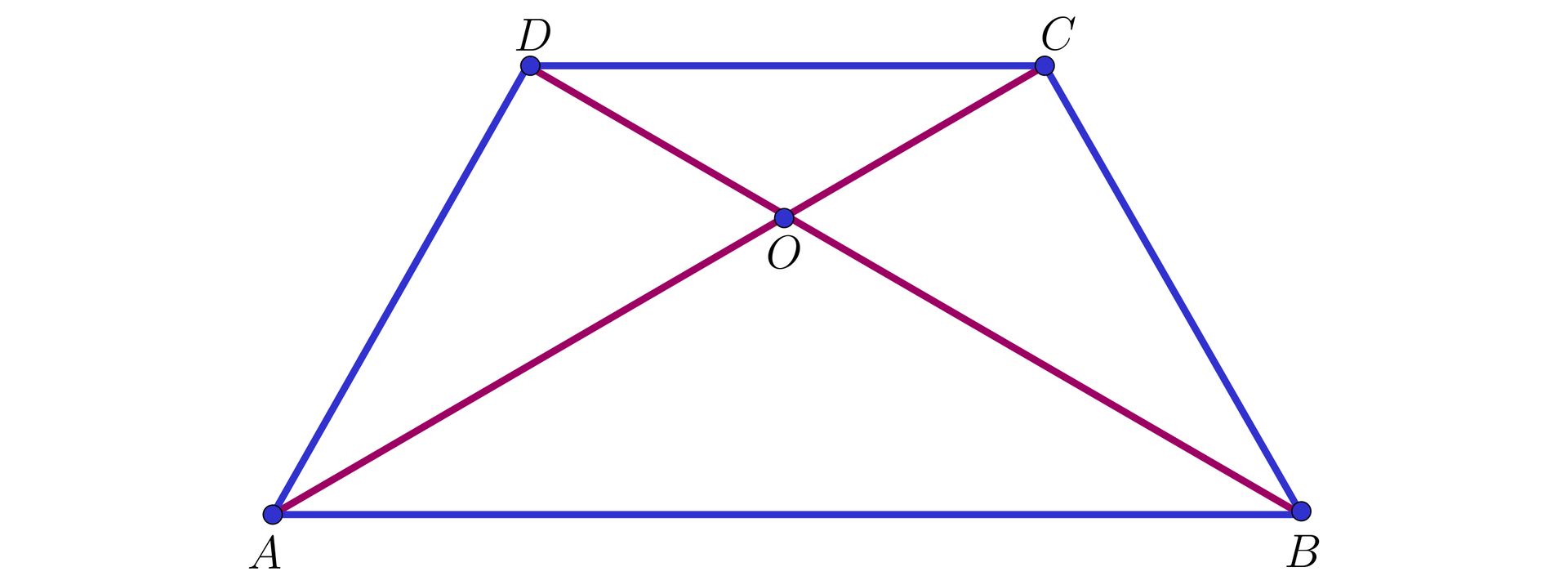
Wiemy, że w opisanym trapezie przekątne i przecinają się w takim punkcie , że . Zatem , a więc .
Pole trapezu jest równe .
Pole trójkąta jest równe . Na bokach i tego trójkąta wybrano takie punkty odpowiednio i , że . Odcinki i przecinają się w punkcie . Obliczymy pola trójkątów: , i .
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku.
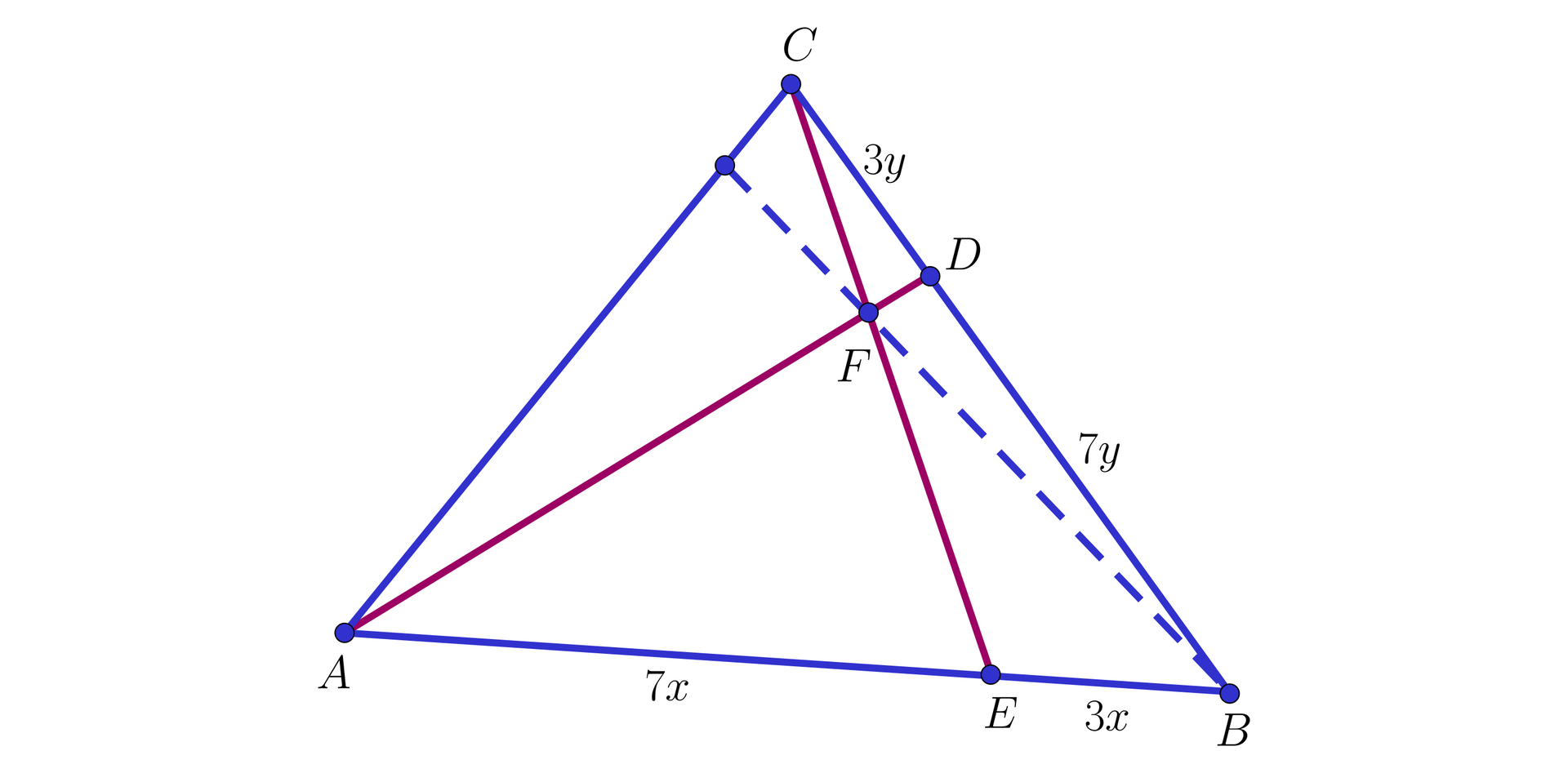
Trójkąty i mają wspólną wysokość. Stosunek ich podstaw .
Analogicznie trójkąty i mają wspólną wysokość. Stosunek ich podstaw .
Niech
i ,
i .
Zauważmy, że trójkąty i mają tą samą wysokość oraz
,
.
Rozwiązmy układ równań.
A stąd otrzymujemy, że , , .
Dany jest równoległobok . Punkt należy do boku , a punkt należy do boku . Prosta przecina prostą w punkcie , a prostą w punkcie .
Wykażemy, że niezależnie od wyboru punktów i pole trójkąta jest równe polu trójkąta .
Dowód
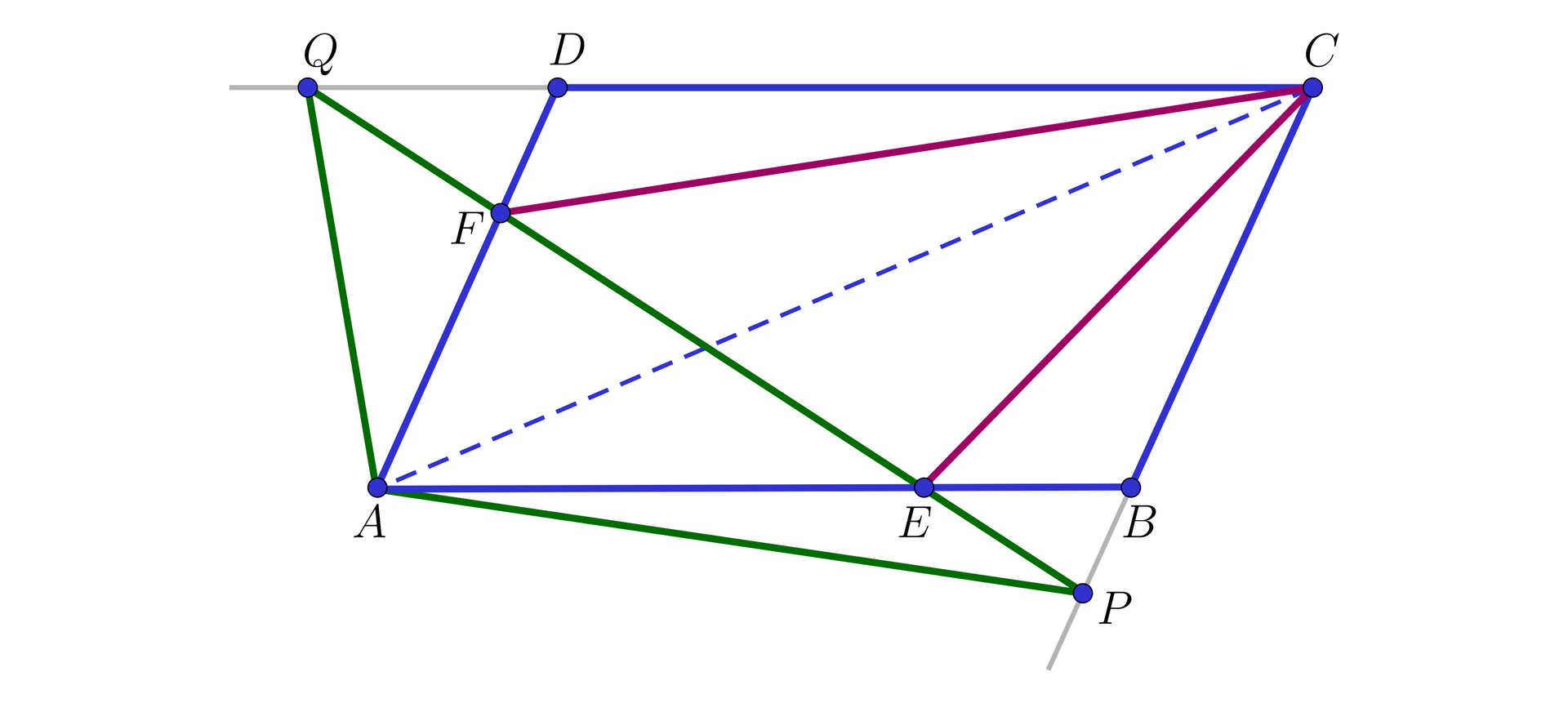
Ponieważ:
więc ,
więc .
(te pary trójkątów mają te same podstawy i równe wysokości).
Wynika stąd, że:
Ponadto:
, oraz
a więc otrzymujemy równość:
Zatem:
.
Koniec dowodu.
Dany jest trójkąt ostrokątny , w którym . Punkt jest spodkiem wysokości tego trójkąta poprowadzonej z wierzchołka . Punkt jest środkiem okręgu opisanego na trójkącie .
Udowodnij, że pola czworokątów oraz są równe.
Dowód
Oznaczmy środek boku przez . Wtedy środkowa dzieli trójkąt na dwa trójkąty o równych polach:
.
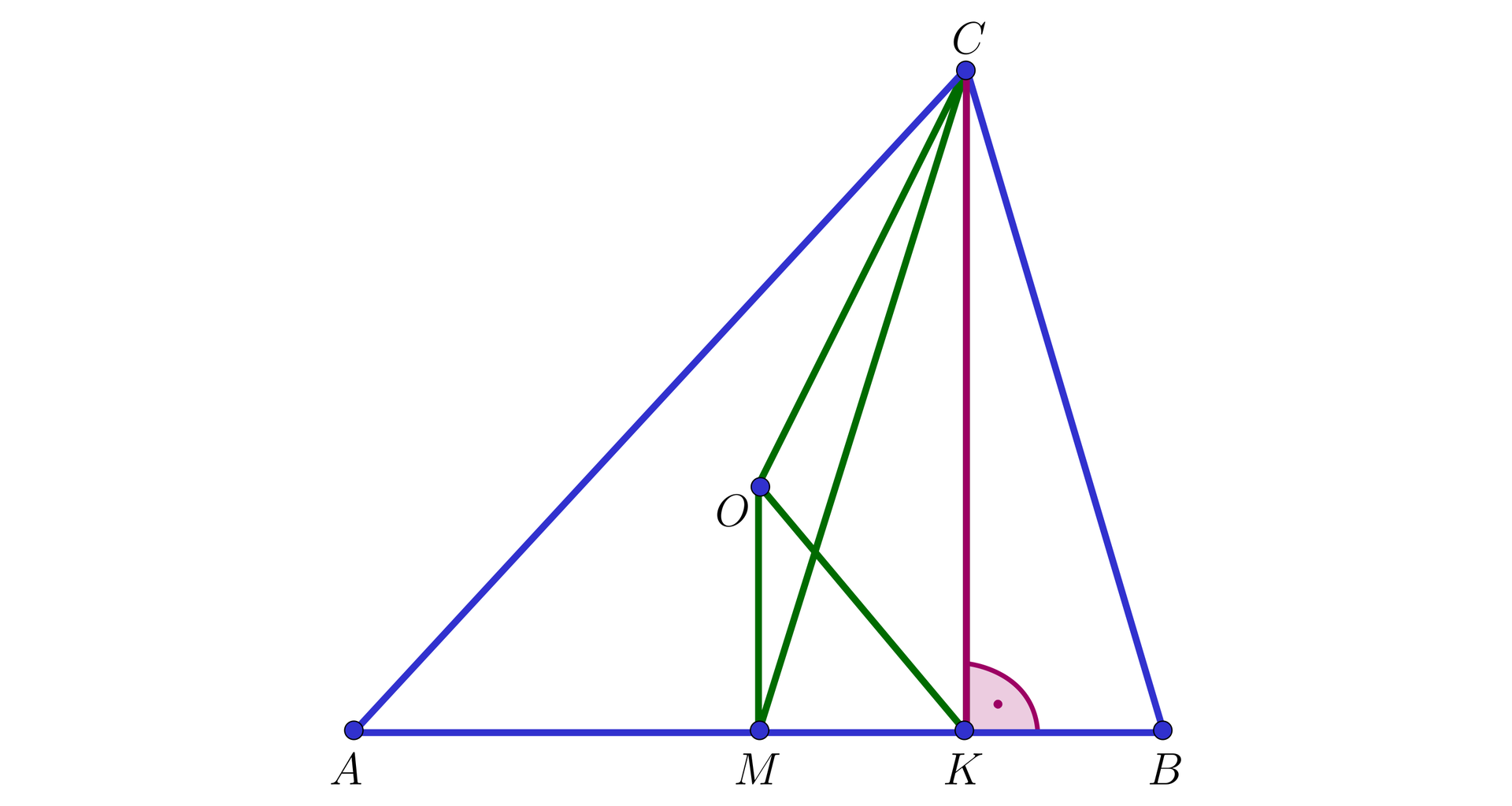
Ponieważ jest środkiem okręgu opisanego na trójkącie , więc trójkąt jest równoramienny, co oznacza, że .
Jednocześnie (jako wysokość opuszczona z na ).
Zatem , czyli czworokąt jest trapezem.
Oznaczmy przez punkt przecięcia przekątnych tego trapezu.
Wówczas pola trójkątów i są równe: .
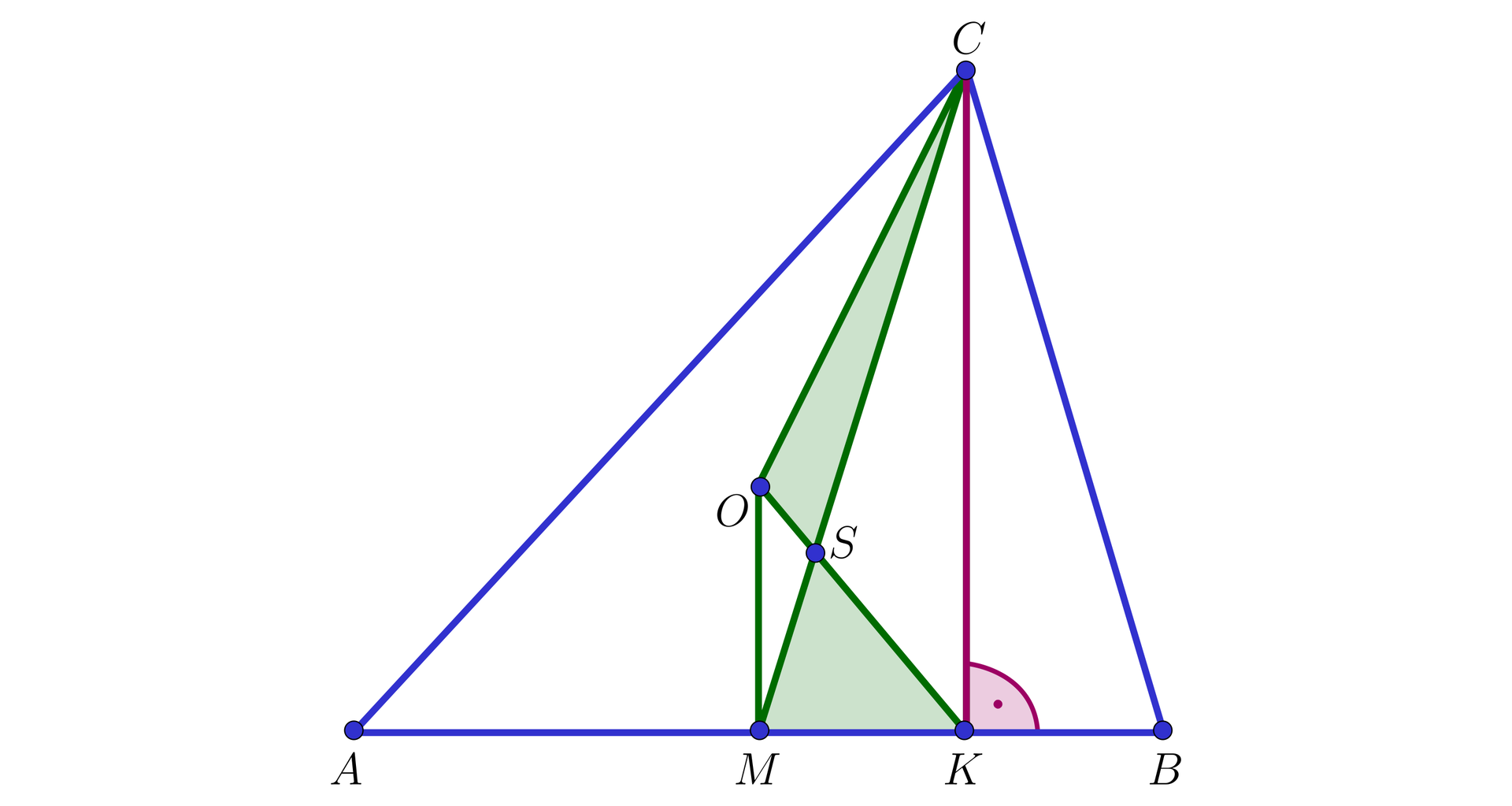
Zauważmy, że:
skąd
.
Ponadto
, a więc , czyli .
Koniec dowodu.
Słownik
wielokąt wypukły, który ma przynajmniej jedną parę boków równoległych
szczególny przypadek trapezu, w którym boki przeciwległe są równoległe i równe