Objętość graniastosłupa prawidłowego trójkątnego jest równa iloczynowi pola podstawy przez wysokość.

RhLPCcbKVgKud

Ilustracja przedstawia graniastosłup prawidłowy trójkątny z krawędziami podstawy równymi a oraz wysokością równą h.

W graniastosłupie prawidłowym trójkątnymgraniastosłup prawidłowy trójkątnygraniastosłupie prawidłowym trójkątnym o objętości równej $1$, pole powierzchni bocznej jest równe sumie pól podstaw. Wyznaczymy długość krawędzi podstawy i długość wysokości tego graniastosłupa.

Rozwiązanie:

Niech $a>0$ oznacza długość krawędzi podstawy oraz $h>0$ długość wysokości rozważanego graniastosłupa. Z warunków zadania wynika, że

$3ah=2\cdot \frac{a^2\sqrt{3}}{4}$ oraz $\frac{a^2\sqrt{3}}{4}h=1$.

Przekształcając równoważnie pierwsze równanie, uzyskujemy kolejno

$3ah=\frac{a^2\sqrt{3}}{2}$

$3h=\frac{a\sqrt{3}}{2}$

$h=\frac{a\sqrt{3}}{6}$.

Następnie, podstawiając powyższą zależność do drugiego równania, otrzymujemy kolejno

$\frac{a^2\sqrt{3}}{4}·\frac{a\sqrt{3}}{6}=1$

$\frac{a^3}{8}=1$

$a=2$.

Możemy wyliczyć długość wysokości

$h=\frac{2\sqrt{3}}{6}=\frac{\sqrt{3}}{3}$.

Zatem krawędź podstawy graniastosłupa ma długość $2$, a wysokość $\frac{\sqrt{3}}{3}$.

Na rysunku przedstawiono graniastosłup prawidłowy trójkątny. Przyjmując że $h=10$ oraz $\cos \alpha =\frac{9}{10}$, obliczymy jego objętość.

R1NQYxxPHdUhM

Ilustracja przedstawia graniastosłup prawidłowy trójkątny $ABCDEF$ z krawędziami podstawy równymi a  oraz wysokością równą h. Zaznaczono przekątną ściany bocznej graniastosłupa tworzącą z krawędzią podstawy kąt o mierze $\alpha$

Rozwiązanie:

Niech $a>0$ oznacza długość krawędzi podstawy, $h>0$ długość wysokości oraz $d>0$ długość przekątnej ściany bocznej rozważanego graniastosłupa. Korzystając z twierdzenia Pitagorasatwierdzenie Pitagorasatwierdzenia Pitagorasa dla trójkąta $ACF$ mamy

$d^2=a^2+h^2=a^2+100$.

Stosujemy twierdzenie kosinusówtwierdzenie cosinusówtwierdzenie kosinusów do trójkąta $ABF$, otrzymujemy kolejno

$a^2=d^2+d^2-2·d·d·\cos \alpha$

$a^2=2\left(a^2+100\right)-2\left(a^2+100\right)·\frac{9}{10}$

$a^2=\frac{1}{5}{a}^2+20$

$a^2=25$

$a=5$.

Możemy obliczyć objętość

$V=\frac{a^2\sqrt{3}}{4}h=\frac{25\sqrt{3}}{4}·10=\frac{125}{2}\sqrt{3}$.

Graniastosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy i nachyloną do płaszczyzny podstawy pod kątem ostrym, którego $\mathrm{tg}\alpha =2\sqrt{3}$. Pole otrzymanego przekroju wynosi $\sqrt{39}$. Stosunek długości wysokości do długości krawędzi podstawy tego graniastosłupa wynosi $2$. Obliczymy objętość tego graniastosłupa.

Rozwiązanie:

R10kC18OcVgZn

Ilustracja przedstawia graniastosłup prawidłowy trójkątny A B C D E F z krawędziami podstawy równymi a  oraz wysokością równą h. Graniastosłup prawidłowy trójkątny przecięto płaszczyzną od punktu R na krawędzi ściany bocznej przechodzącą przez krawędź podstawy AC i nachyloną do płaszczyzny podstawy pod kątem $\alpha$.

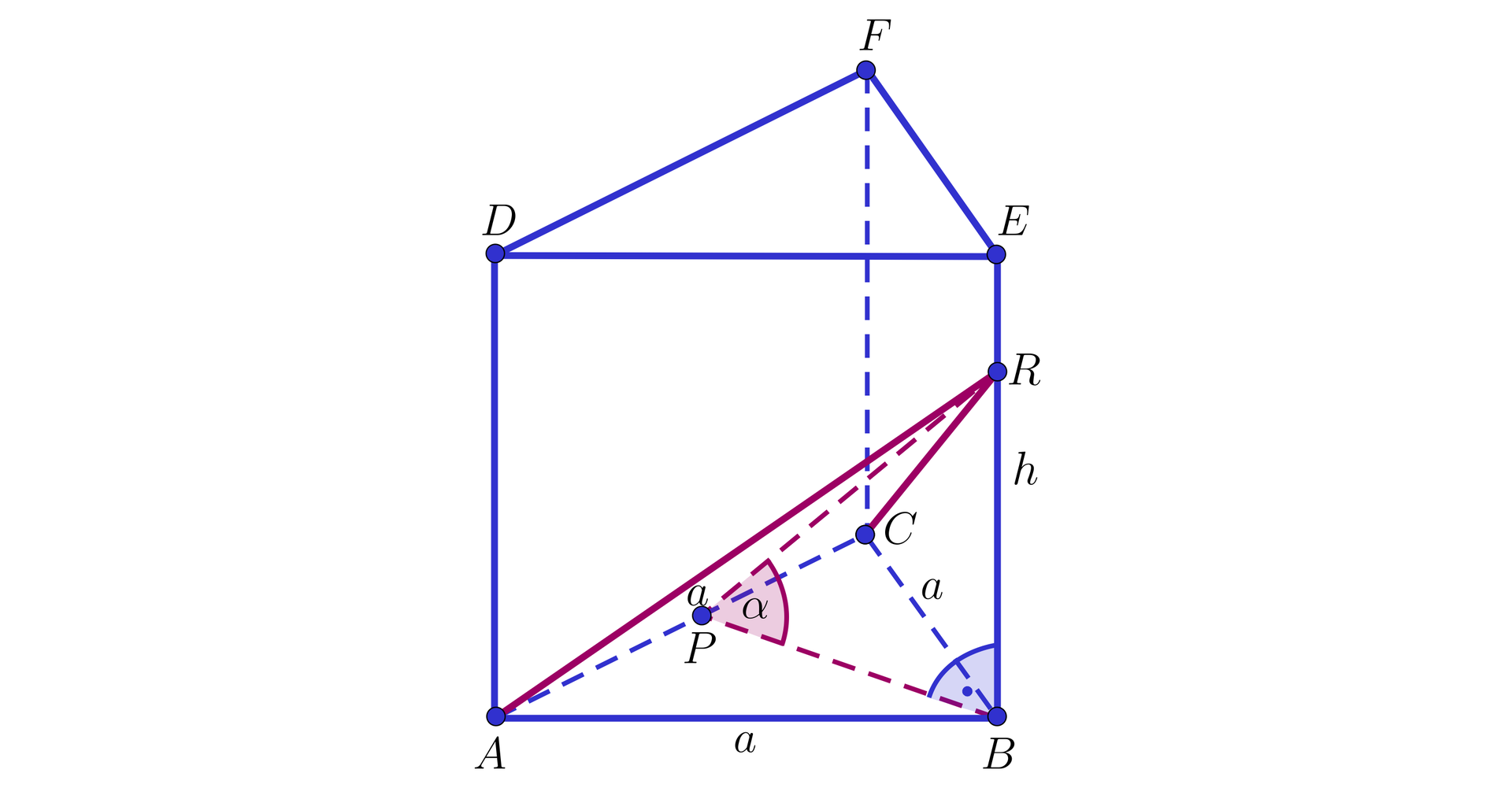
Niech $a>0$ oznacza długość krawędzi podstawy oraz $h>0$ długość wysokości rozważanego graniastosłupa. Zauważmy, że przekrój jest trójkątem równoramiennym, a nie trapezem wtedy i tylko wtedy gdy punkt $R$ znajduje się na krawędzi $EB$. Dzieję się tak, gdy

$\mathrm{tg}\alpha \le \frac{h}{\frac{a\sqrt{3}}{2}}=\frac{2h}{a\sqrt{3}}=\frac{2\sqrt{3}h}{3a}=\frac{4\sqrt{3}}{3}$.

Ostatnia równość wynika z faktu, że stosunek długości wysokości do długości krawędzi podstawy tego graniastosłupa wynosi $2$. Zatem pole trójkąta równoramiennego wynosi $P_{ACR}=\sqrt{39}$ i wysokości $h_{ACR}>0$. Z warunków zadania mamy

$\mathrm{tg}\alpha =2\sqrt{3}$ oraz $P_{ACR}=\frac{1}{2}a{h}_{ACR}=\sqrt{39}$ i $h=2a$.

Z trójkąta $RPB$ otrzymujemy

$\frac{\left|BR\right|}{\left|PB\right|}=2\sqrt{3}$,

gdzie odcinek $\left|PB\right|=\frac{a\sqrt{3}}{2}$ jest wysokością podstawy. Otrzymujemy kolejno

$\frac{\left|BR\right|}{{\displaystyle \frac{a\sqrt{3}}{2}}}=2\sqrt{3}$

$\left|BR\right|=3a$.

Możemy teraz wyznaczyć zależność wysokości trójkąta $ACR$ od długości krawędzi podstawy. Korzystając z twierdzenia Pitagorasa dla trójkąta $RPB$ otrzymujemy

$h_{ACR}=\sqrt{9a^2+\frac{3a^2}{4}}=\frac{\sqrt{39}}{2}a$.

Podstawiając tę zależność do wzoru na pole przekroju graniastosłupa otrzymujemy

$P_{ACR}=\frac{1}{2}a{h}_{ACR}=\frac{1}{2}a·\frac{\sqrt{39}}{2}a=\frac{\sqrt{39}}{4}{a}^2=\sqrt{39}$.

Stąd $a=2$ oraz $h=4$. Możemy obliczyć objętość

$V=\frac{a^2\sqrt{3}}{4}h=\frac{4\sqrt{3}}{4}·4=4\sqrt{3}$.

W graniastosłupie prawidłowym trójkątnym krawędź podstawy jest równa $4$, a tangens kąta jaki przekątna ściany bocznej tworzy z sąsiednią ścianą boczną wynosi $\frac{\sqrt{15}}{5}$. Obliczymy objętość tego graniastosłupa.

Rozwiązanie:

Rozważmy graniastosłup prawidłowy trójkątny przedstawiony na rysunku.

R8ubrB07bHNab

Ilustracja przedstawia graniastosłup prawidłowy trójkątny A B C D E F. Środek krawędzi podstawy B C oznaczono punktem P. W środku graniastosłupa powstał trójkąt prostokątny A P F. Kąt przy wierzchołku F ma miarę $\alpha$.

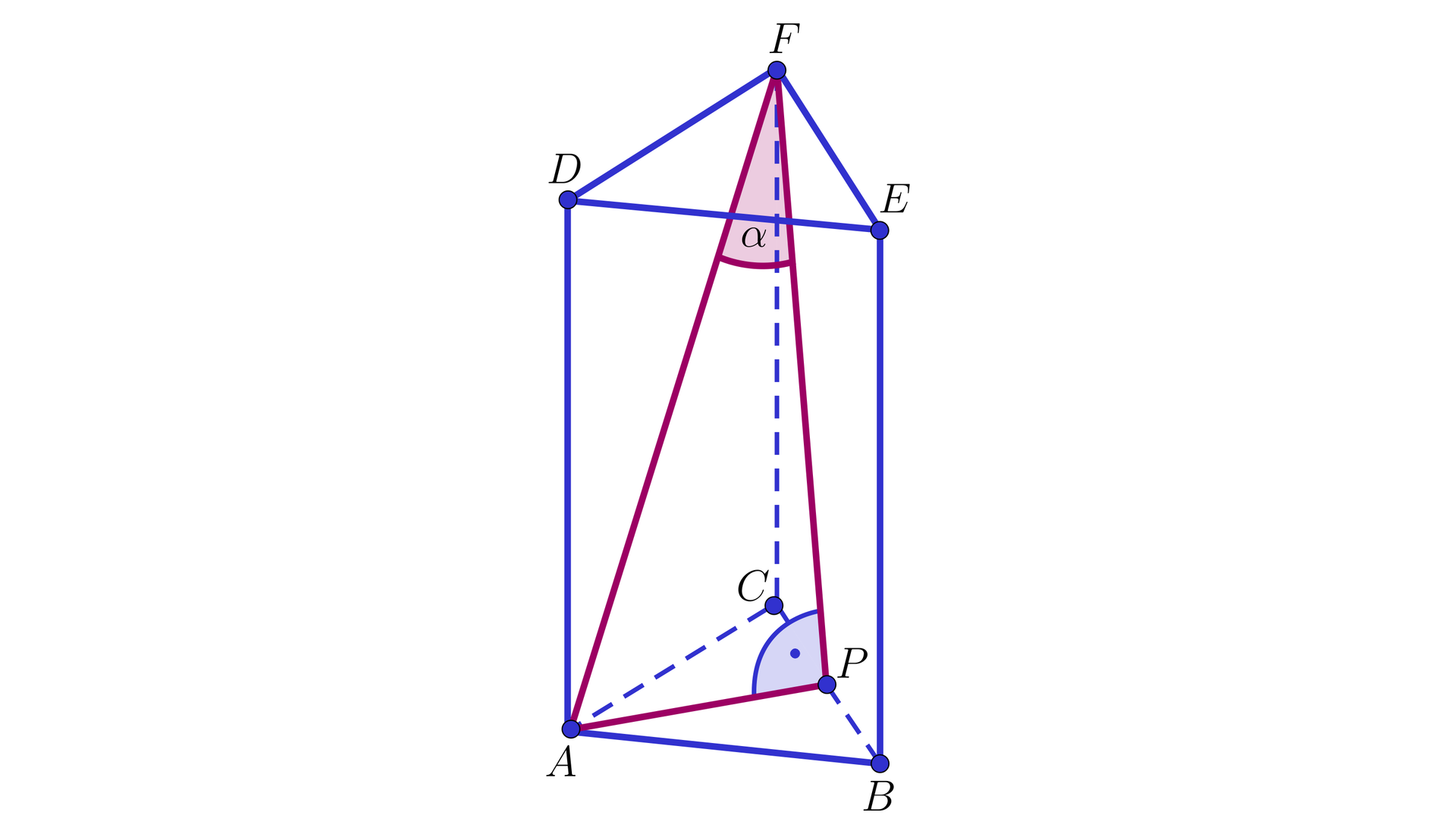
Niech $a>0$ oznacza długość krawędzi podstawy oraz $h>0$ długość wysokości rozważanego graniastosłupa. Z treści zadania wynika, że $a=\left|AB\right|=\left|BC\right|=\left|AC\right|=4$. Odcinek $\left|AP\right|=\frac{a\sqrt{3}}{2}=2\sqrt{3}$ jest wysokością podstawy. Z warunków zadania otrzymujemy kolejno

$\mathrm{tg}\alpha =\frac{\left|AP\right|}{\left|PF\right|}$

$\frac{2\sqrt{3}}{\left|PF\right|}=\frac{\sqrt{15}}{5}$

$\left|PF\right|=2\sqrt{5}$.

Korzystając z twierdzenia Pitagorasa dla trójkąta $FCP$ otrzymujemy

${\left|PF\right|}^2=h^2+\frac{1}{4}{a}^2$, stąd mamy $h=4$.

Możemy obliczyć objętość

$V=\frac{a^2\sqrt{3}}{4}h=\frac{16\sqrt{3}}{4}·4=16\sqrt{3}$.

W graniastosłupie prawidłowym trójkątnym pole powierzchni całkowitej jest równe $3\sqrt{3}$. Kosinus kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej wynosi $\frac{2\sqrt{13}}{13}$. Obliczymy objętość tego graniastosłupa.

Rozwiązanie:

R1dBj5PFgTVob

Ilustracja przedstawia graniastosłup prawidłowy trójkątny A B C D E F. Środek krawędzi podstawy B C oznaczono punktem P. W środku graniastosłupa powstał trójkąt prostokątny A P F. Kąt przy wierzchołku F ma miarę $\alpha$.

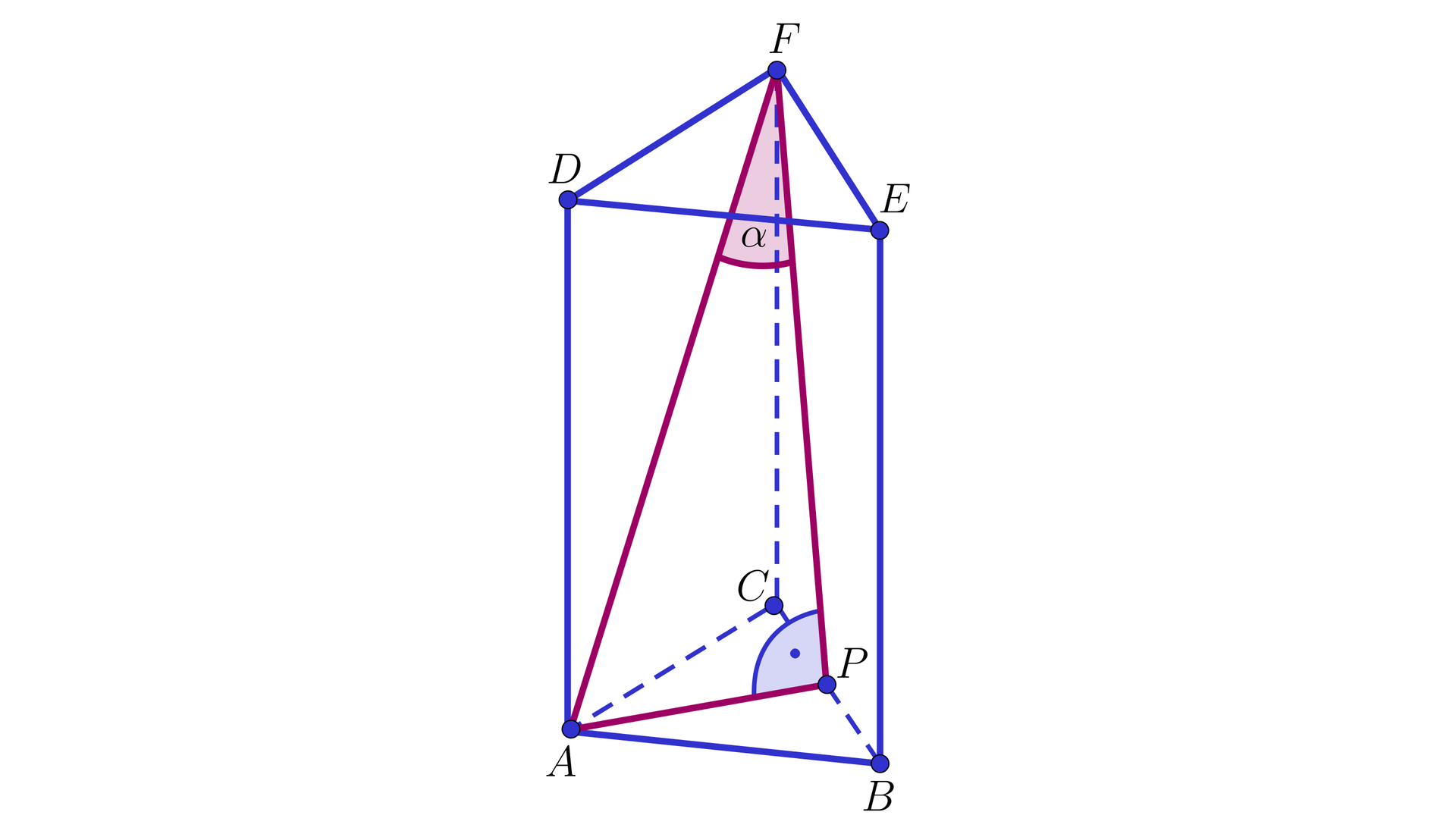
Niech $a>0$ oznacza długość krawędzi podstawy oraz $h>0$ długość wysokości rozważanego graniastosłupa. Korzystając z twierdzenia Pitagorasa kolejno dla trójkątów $ACF$ i $PCF$ otrzymujemy, że

$\left|AF\right|=\sqrt{h^2+a^2}$ oraz $\left|FP\right|=\sqrt{h^2+\frac{1}{4}{a}^2}$.

Z warunków zadania mamy kolejno

$\cos \alpha =\frac{\left|FP\right|}{\left|AF\right|}$

$\frac{\sqrt{h^2+{\displaystyle \frac{1}{4}}{a}^2}}{\sqrt{h^2+a^2}}=\frac{2\sqrt{13}}{13}$

$13\left(h^2+\frac{1}{4}{a}^2\right)=4\left(h^2+a^2\right)$

$9h^2=\frac{3}{4}{a}^2$

$h=\frac{\sqrt{3}}{6}a$.

Podstawiamy tę zależność do wzoru na pole powierzchni całkowitej graniastosłupa. Otrzymujemy kolejno

$3ah+\frac{a^2\sqrt{3}}{2}=3\sqrt{3}$

$3a·\frac{\sqrt{3}}{6}a+\frac{a^2\sqrt{3}}{2}=3\sqrt{3}$

$a^2=3$

$a=\sqrt{3}$ zatem $h=\frac{1}{2}$.

Możemy obliczyć objętość

$V=\frac{a^2\sqrt{3}}{4}h=\frac{3\sqrt{3}}{4}·\frac{1}{2}=\frac{3\sqrt{3}}{8}$.

graniastosłup prosty, którego podstawą jest trójkąt równoboczny

w dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta

w dowolnym trójkącie, kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi