Przeczytaj
Przypomnijmy najpierw niektóre wzory na pola wielokątów z wykorzystaniem funkcji sinus:
Wzory na pola wielokątów z wykorzystaniem funkcji sinus | |
|---|---|
Trójkąt o bokach długości , i kącie między nimi . | |
Równoległobok o bokach długości , i kącie między nimi . | |
Równoległobok o przekątnych długości , i kącie między nimi . | |
Romb o boku długości i kącie . | |
Pole równoległoboku o kącie ostrym wynosi . Obliczymy długości jego boków, jeśli pozostają one w stosunku .
Rozwiązanie
Oznaczymy długości boków równoległoboku przez i . Zatem:
.
Korzystając ze wzoru na sinus sumy kątów wyznaczymy :
.
Zatem:
Boki równoległoboku mają długości: i .
Pole koła wpisanego w romb o kącie ostrym o mierze wynosi . Wyznaczymy pole tego rombu.
Rozwiązanie
Wysokość rombu, w którym wpisano koło o promieniu długości , jest równa :
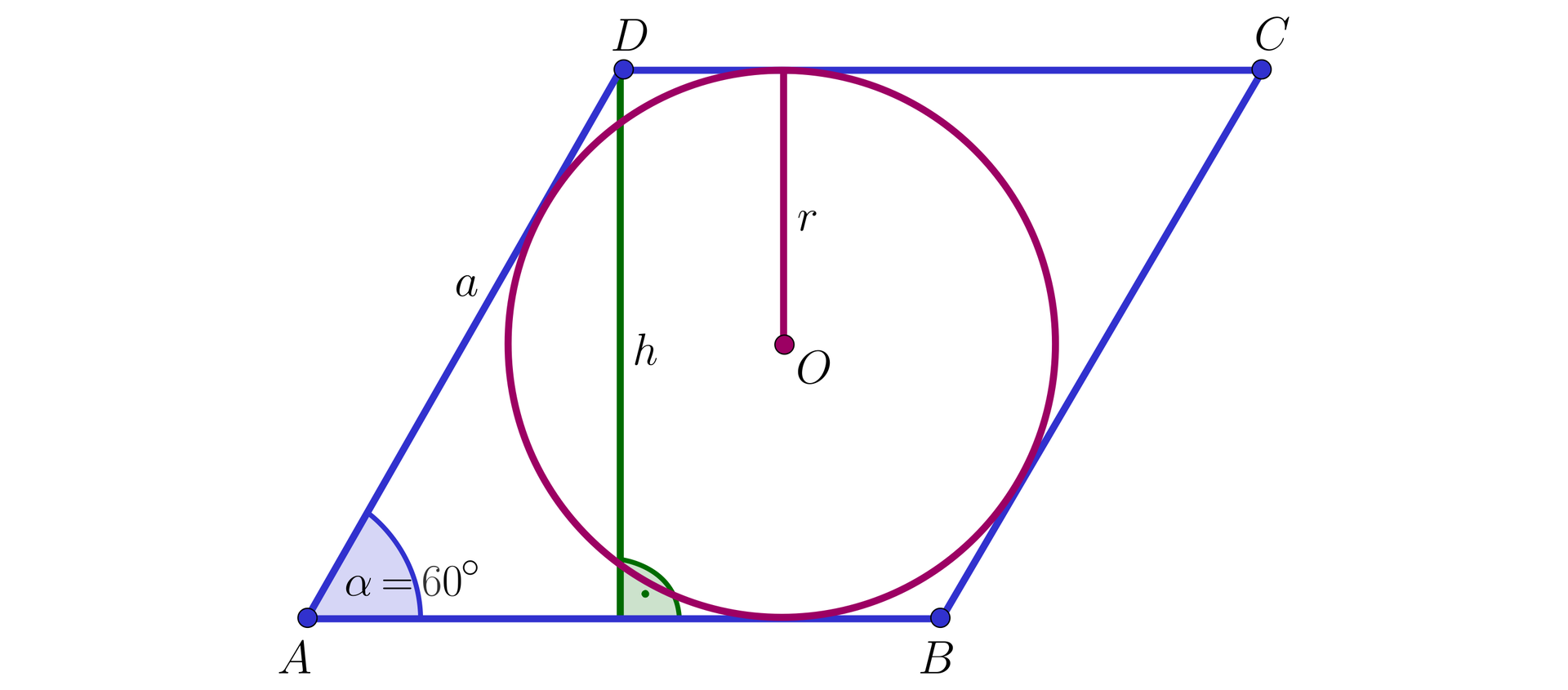
Wyznaczymy długość promienia koła wpisanego w romb:
Zatem wysokość tego rombu ma długość: .
Wykorzystamy definicję sinusa kąta ostrego w trójkącie prostokątnymsinusa kąta ostrego w trójkącie prostokątnym:
Obliczamy pole rombu:
.
Bok trójkąta ma długość , zaś bok jest dwa razy krótszy niż bok . Sinus kąta ostrego wynosi . Wyznaczymy pole tego trójkąta, jeśli .
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku:

Do wyznaczenia długości boku zastosujemy twierdzenie cosinusówtwierdzenie cosinusów:
Wartość wyznaczymy z jedynki trygonometrycznejjedynki trygonometrycznej:
Zatem:
Stąd: lub
Tylko dla długość boku jest większa od , co daje: .
Pole trójkąta jest równe:
.
Obliczymy pole trapezu równoramiennego, którego krótsza podstawa ma długość a miara kąta ostrego wynosi , jeśli promień okręgu opisanego na tym trapezie ma długość .
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku:
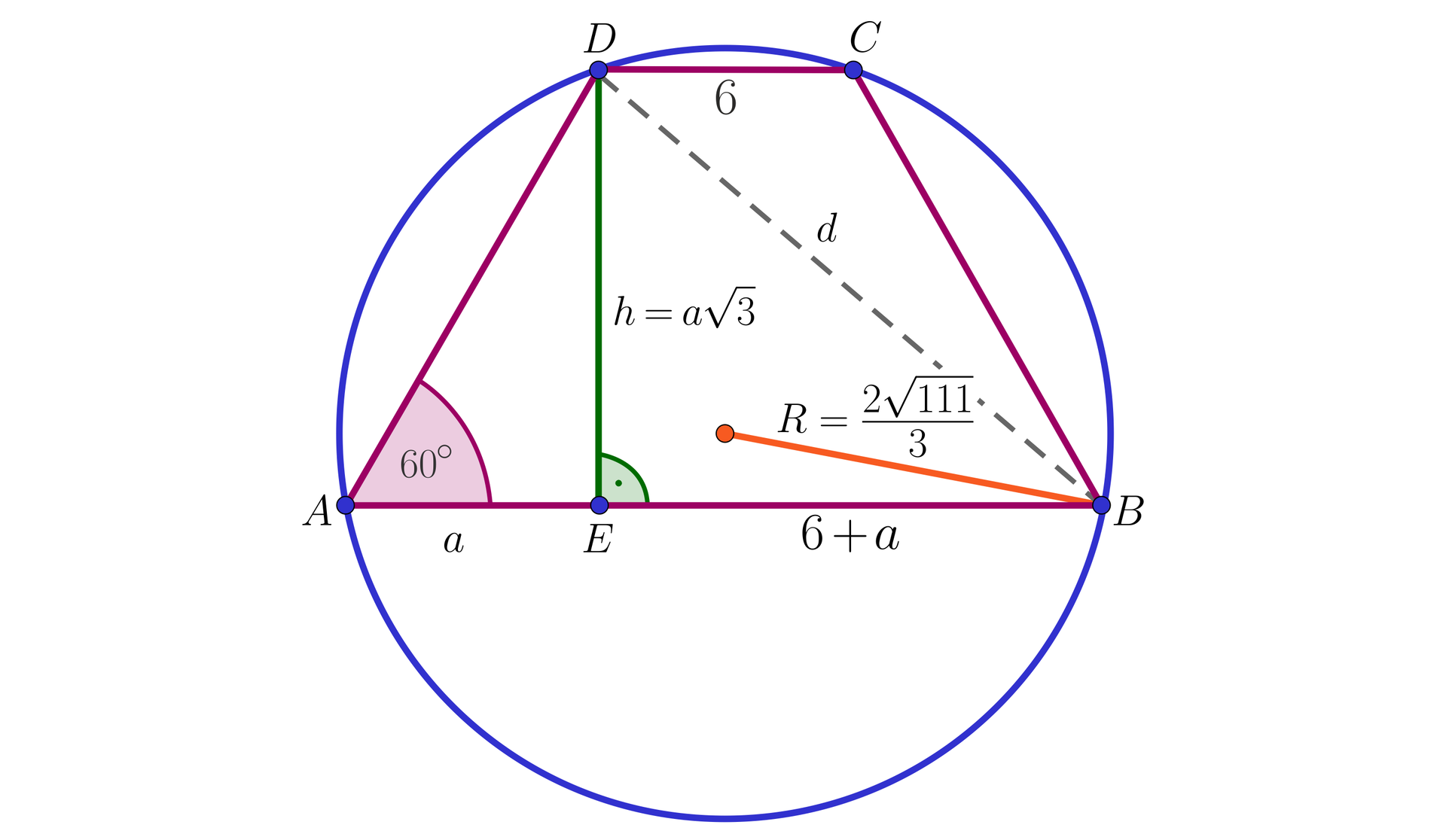
Zauważmy, że okrąg opisany na trapezie jest jednocześnie okręgiem opisanym na trójkącie . Zastosujemy zatem twierdzenie sinusówtwierdzenie sinusów:
Z twierdzenia Pitagorasa dla trójkąta :
lub
Zatem: .
Stąd:
Udowodnimy, że dla dowolnego czworokąta o bokach długości , , , , który można wpisać w okrąg, jego pole wyraża się wzorem:
gdzie oznacza połowę obwodu czworokąta.
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku:
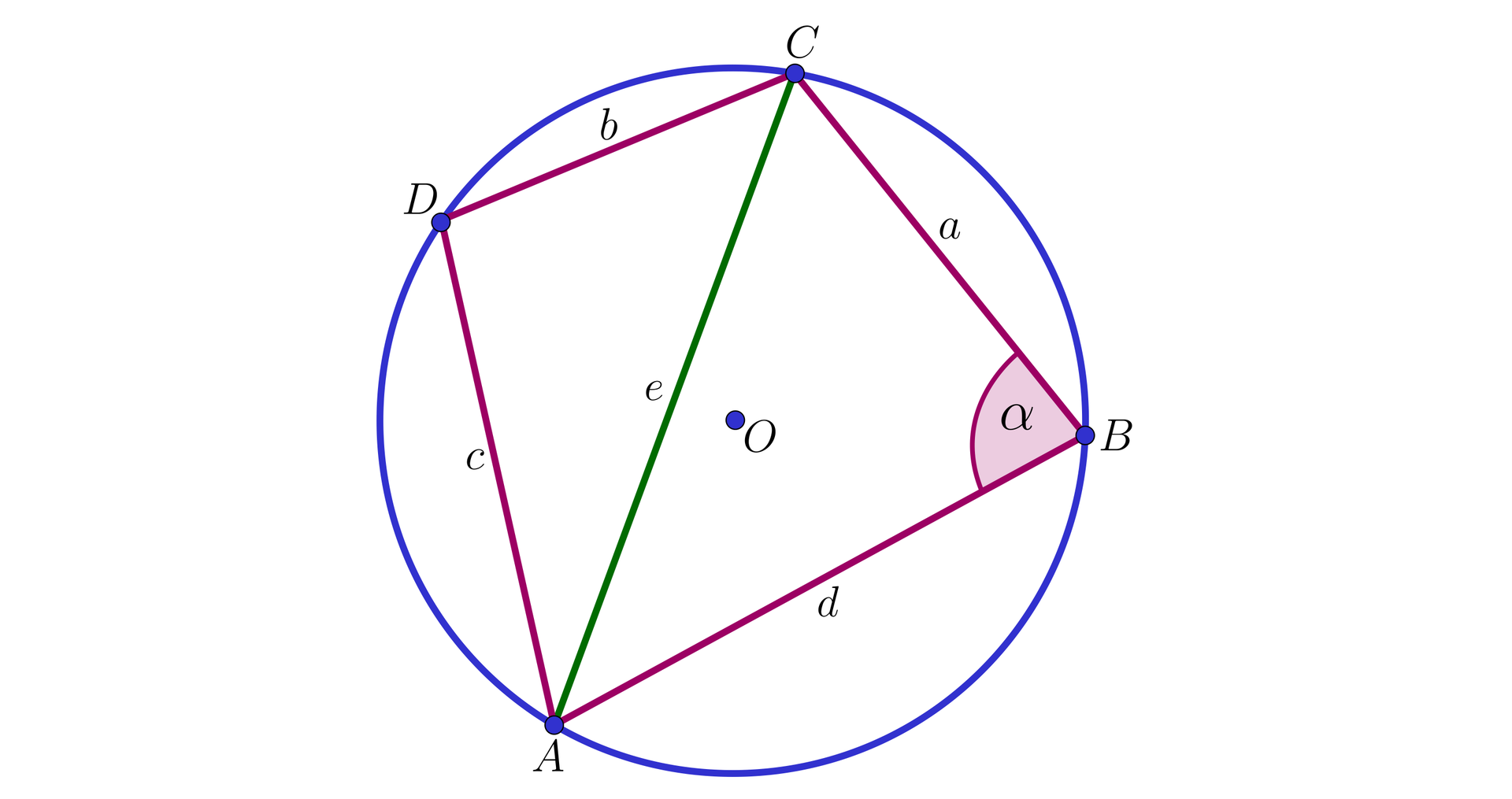
Czworokąt jest sumą trójkątów i , zatem:
Ponieważ na czworokącie da się opisać okrąg, to i .
Stosując dwukrotnie twierdzenie cosinusów otrzymujemy:
Zatem:
, co daje: i stąd:
Zastosujemy następnie jedynkę trygonometryczną:
Zauważmy, że:
Zatem:
Oznaczmy przez obwód czworokąta: .
Mamy zatem:
Słownik
stosunek długości przyprostokątnej leżącej naprzeciw kąta do długości przeciwprostokątnej
w dowolnym trójkącie kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków minus podwojony iloczyn długości tych boków przez cosinus kąta leżącego między nimi
dla dowolnego kąta suma kwadratów wartości sinusa i cosinusa tego kąta jest równa
w dowolnym trójkącie stosunek długości boku do sinusa dowolnego kąta jest stały i równy średnicy okręgu opisanego na trójkącie