Przeczytaj

Optymalizacja

Definicja: Optymalizacja

Optymalizacją nazywamy metodę najlepszego rozwiązania z punktu widzenia określonego kryterium. W matematyce jest to problem polegający na znalezieniu ekstremum funkcjiekstremum funkcjiekstremum funkcji, przy ustalonym warunku.

OptymalizacjaoptymalizacjaOptymalizacja w przypadku funkcji kwadratowej składa się z następujących kroków:

analiza treści zadania i wskazanie wielkości, którą będziemy optymalizować,
zapisanie wzoru odpowiedniej funkcji kwadratowej,
obliczenie współrzędnych wierzchołka funkcji kwadratowej.

Funkcja kwadratowa posiada dokładnie jedno ekstremum w punkcie, który jest wierzchołkiem wykresu funkcji kwadratowej. Oznacza to, że nie musimy szukać ekstremum lokalnego, możemy od razu przejść do wyznaczania ekstremum globalnego funkcji.

Przypomnijmy definicję maksimum oraz minimum globalnego funkcji.

Maksimum, minimum globalne

Definicja: Maksimum, minimum globalne

Niech dana będzie funkcja rzeczywista $f : X ⟶ ℝ$ . Powiemy, że funkcja $f$ osiąga maksimum globalne w punkcie $x_{0} \in X$ , jeżeli dla dowolnego punktu $x \in X$ spełniona jest nierówność

f (x_{0}) \geq f (x)

Analogicznie, powiemy, że funkcja $f$ osiąga minimum globalne w punkcie $x_{0} \in X$ , jeżeli dla dowolnego punktu $x \in X$ zachodzi nierówność

f (x_{0}) \leq f (x)

Liczbę $f (x_{0})$ nazywamy wówczas (odpowiednio) największą lub najmniejszą wartością funkcji $f$ w zbiorze $X$ .

W przypadku funkcji kwadratowej jest jednak inaczej, co wynika z kształtu paraboli, będącej jej wykresem. Przeanalizujmy poniższe wykresy.

Ra3Ij24tfCuYw

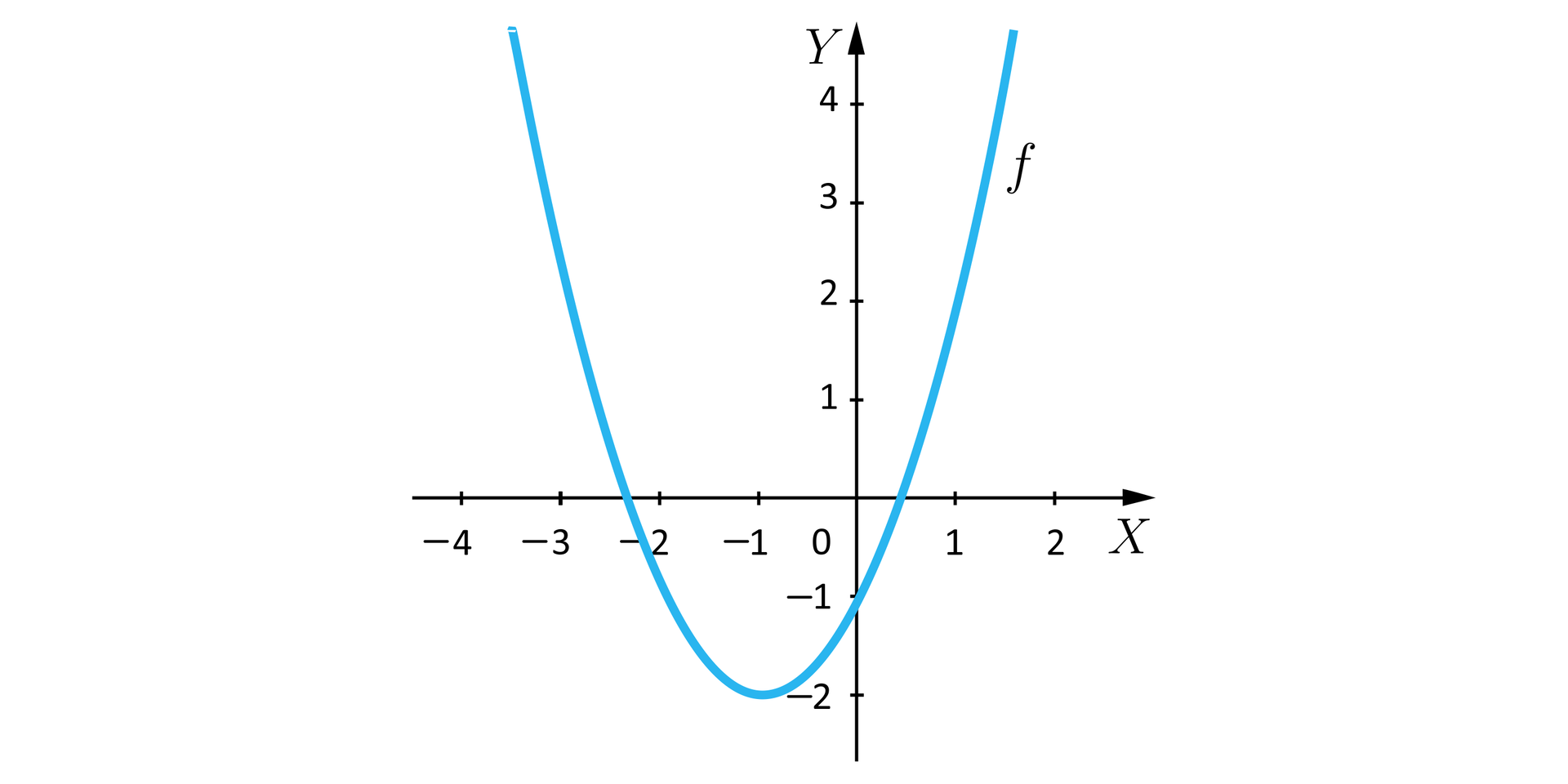
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus czterech do dwóch, oraz z pionową osią Y od minus dwóch do czterech. Na płaszczyźnie narysowano wykres funkcji fx. Wykresem funkcji jest parabola o wierzchołku w punkcie -2;-3 i ramionach skierowanych w górę.

RjDNJz7f8ar68

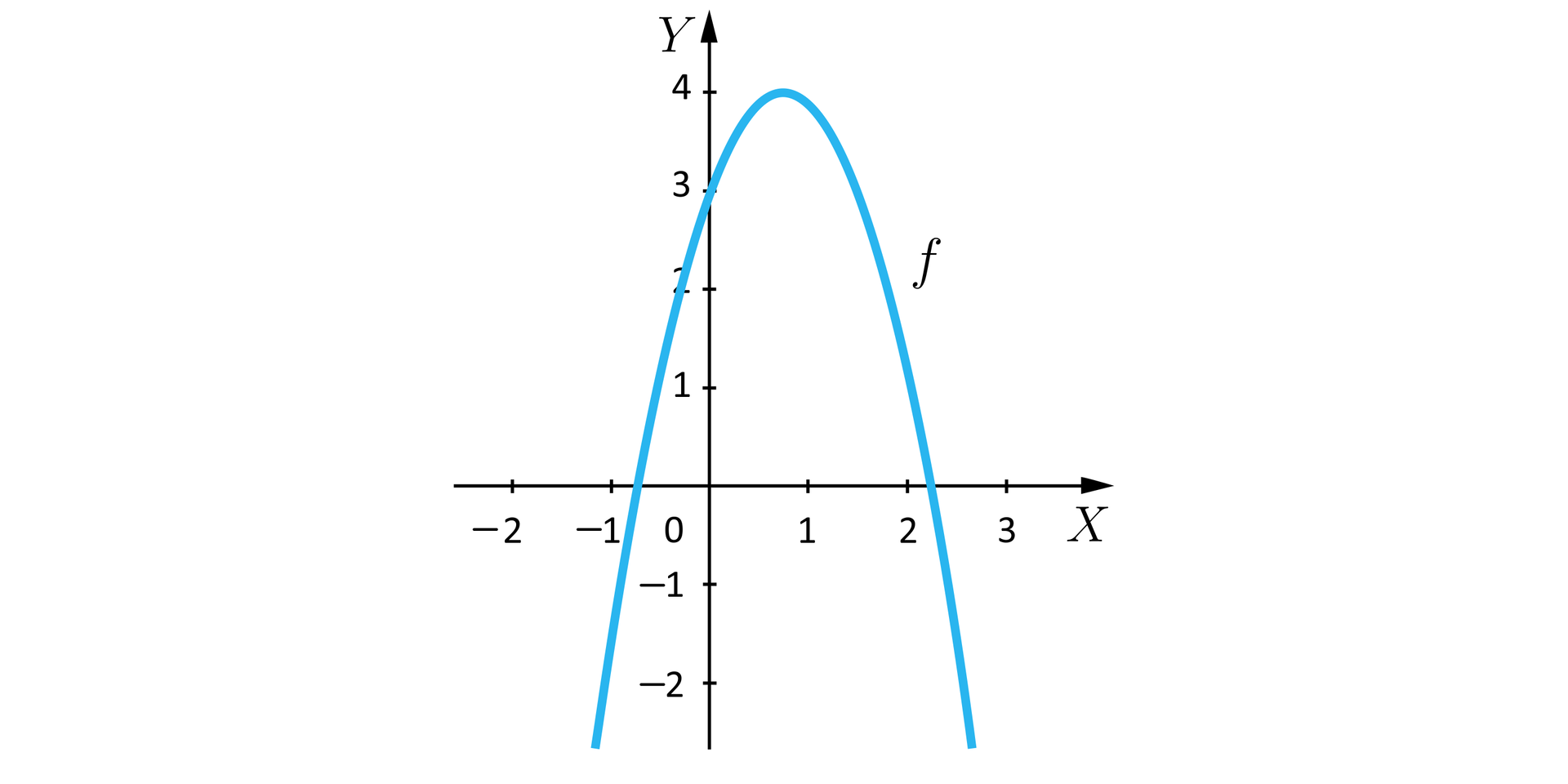
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus dwóch do trzech, oraz z pionową osią Y od minus dwóch do czterech. Na płaszczyźnie narysowano wykres funkcji fx. Wykresem funkcji jest parabola o wierzchołku w punkcie 1;4 i ramionach skierowanych do dołu.

Każda parabola, będąca wykresem funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2} + b x + c$ , gdzie $a \neq 0$ , ma dokładnie jeden wierzchołek. Druga współrzędna punktu, będącego wierzchołkiem tej paraboli odpowiada największej lub najmniejszej wartości przyjmowanej przez zadaną funkcję kwadratową.

O tym, czy jest to minimum, czy maksimum decyduje wartość współczynnika $a$ przy wyrażeniu $x^{2}$ .

Ważne!

Funkcja kwadratowa $f (x) = a x^{2} + b x + c$ :

dla $a > 0$ osiąga wartość najmniejszą w wierzchołku paraboli, będącej wykresem funkcji $f$ ,
dla $a < 0$ osiąga wartość największą w wierzchołku paraboli, będącej wykresem funkcji $f$ .

Przykład 1

Arek i Marek grają w grę, która polega na wyznaczeniu największego iloczynu dwóch liczb, gdy dana jest suma tych liczb. W grze wygrywa się, gdy jeden z graczy wymieni takie liczby, których suma jest równa $10$ , a iloczyn tych liczb jest największy. Wyznaczymy te liczby.

Rozwiązanie:

Niech $x$ i $y$ będą szukanymi liczbami.

Układamy warunek, który przedstawia zależność z zadania: $x + y = 10$ .

Z tego warunku otrzymujemy, że: $y = 10 - x$ .

Zapisujemy wzór funkcji kwadratowej, która określa iloczyn liczb $x$ i $y$ , ale w zależności od zmiennej $x$ .

$f (x) = x \cdot y = x \cdot (10 - x) = - x^{2} + 10 x$ .

Otrzymujemy funkcję kwadratową, której wykres jest parabolą z ramionami skierowanymi do dołu.

Zatem funkcja $f$ przyjmuje wartość największą w wierzchołku paraboli, będącej jej wykresem.

Wyznaczamy współrzędną $p$ wierzchołka paraboli.

Otrzymujemy $p = \frac{- b}{2 a} = \frac{- 10}{2 \cdot (- 1)} = 5$ , czyli $x = 5$ .

Dla $x = 5$ mamy $y = 10 - 5 = 5$ .

Iloczyn tych liczb jest największy, gdy $x = 5$ i $y = 5$ .

Zatem jeden z graczy wygra grę, gdy poda obie liczby równe $5$ .

Dodatkowo możemy obliczyć wartość tego iloczynu. W tym celu wystarczy znaleźć wielkość $q$ .

$q = f (p) = f (5) = - 5^{2} + 10 \cdot 5 = - 25 + 50 = 25$

Przykład 2

Mamy $200$ metrów siatki ogrodzeniowej. Jaką maksymalną, prostokątną powierzchnię możemy ogrodzić?

Rozwiązanie:

Oznaczmy przez $x$ – długość oraz $y$ – szerokość działki.

Z warunku w zadaniu wiemy, że obwód działki wynosi $200$ metrów.

Otrzymujemy rówanie: $2 x + 2 y = 200$ .

Po uproszczeniu mamy, że $x + y = 100$ , więc $y = 100 - x$ .

Z treści zadania wiemy, że $x > 0$ , więc $y \in (0, 100)$ .

Określamy odpowiednią funkcję następująco: $f (x) = x \cdot y = x \cdot (100 - x) = - x^{2} + 100 x$ .

Otrzymaliśmy funkcję kwadratową, której wykres jest parabolą z ramionami skierowanymi do dołu.

Zatem funkcja $f$ przyjmuje wartość największą w wierzchołku.

Wyznaczamy współrzędną $p$ wierzchołka paraboli, będącej wykresem funkcji $f$ .

Otrzymujemy, że $p = \frac{- b}{2 a} = \frac{- 100}{2 \cdot (- 1)} = 50$ , czyli $x = 50$ .

Dla $x = 50$ mamy $y = 50$ .

Aby działka miała największe pole powierzchni, powinna być kwadratem o boku $50$ .

Przykład 3

Strona książki ma kształt prostokąta o obwodzie równym $72 cm$ . Obliczymy, jakie wymiary powinna mieć strona tej książki, aby zapewnić maksymalną powierzchnię druku, przy założeniu, że marginesy boczne i dolne mają szerokość $1 cm$ , a margines górny $2 cm$ .

Rozwiązanie:

Niech $x$ i $y$ będą wymiarami strony w kształcie prostokąta $(x > 0, y > 0)$ . Wykonajmy rysunek pomocniczy do zadania:

R1SMJJS6TNVH8

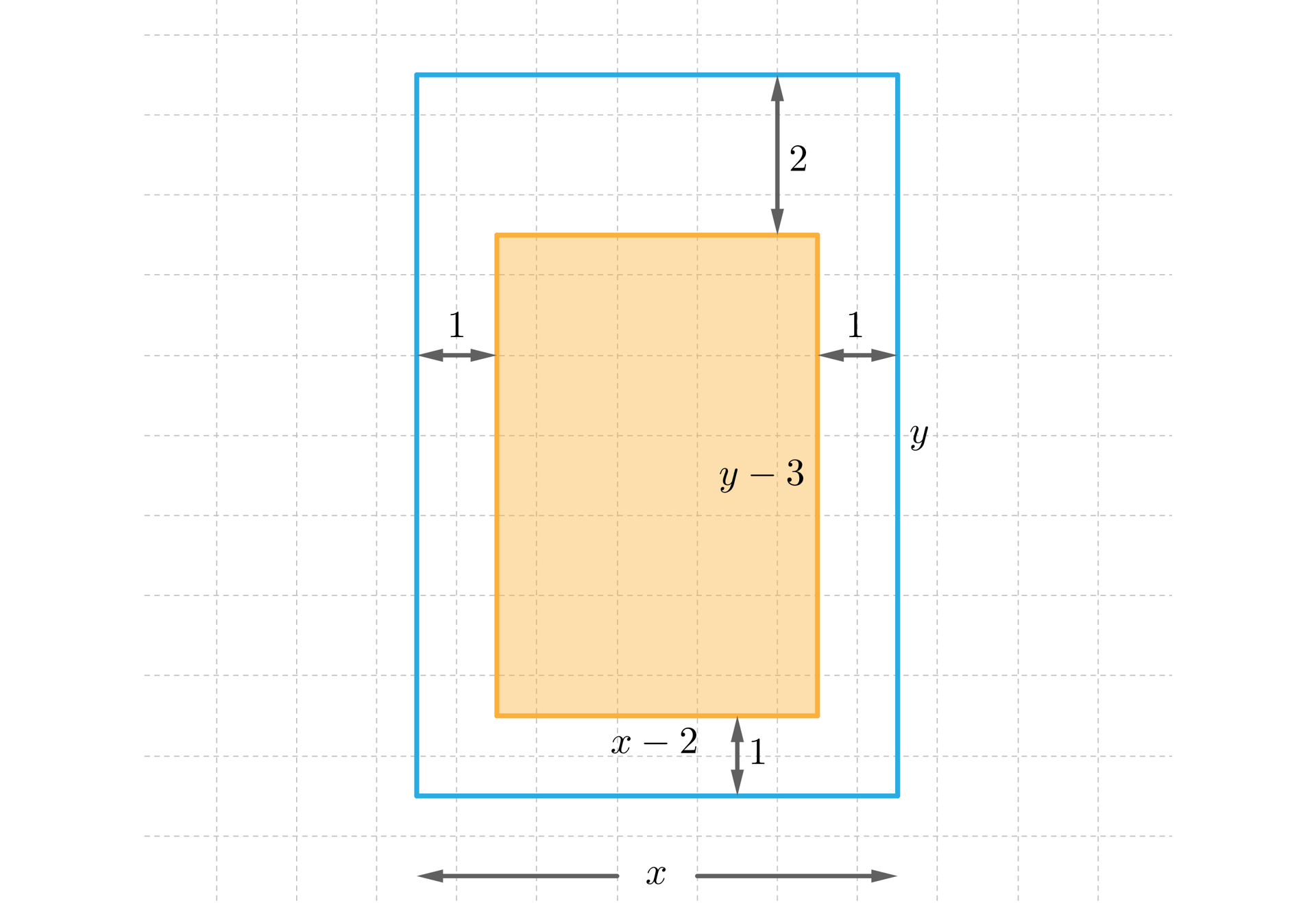
Na ilustracji przedstawiono niebieską ramkę w kształcie prostokąta. Krótszy bok oznaczono x, natomiast dłuższy y. Wewnątrz ramki, znajduje się pomarańczowy prostokąt z zamalowanym polem. Długości jego boków wynoszą odpowiednio x-2, oraz y-3. Pomarańczowy prostokąt jest odsunięty od krawędzi ramki o dwie jednostki w dół od krawędzi górnej, jedną jednostkę w górę od krawędzi dolnej, jedną jednostkę od krawędzi lewej, oraz prawej.

Ponieważ obwód tego prostokąta jest równy $72 cm$ , zatem:

$2 x + 2 y = 72$

Wobec tego $y = 36 - x$ oraz $x \in (0, 36)$ .

Niech $f$ będzie funkcją, która opisuje pole powierzchni strony do druku. Wówczas:

$f (x) = (x - 2) \cdot (y - 3) = (x - 2) (33 - x)$

Otrzymujemy wzór funkcji kwadratowej, której wykresem jest parabola z ramionami skierowanymi do dołu. Zauważmy, że miejscami zerowymi paraboli, będącej wykresem funkcji $f$ są liczby $2$ oraz $33$ . Funkcja przyjmuje wartość największą w wierzchołku paraboli, będącej jej wykresem. Pierwsza współrzędna $p$ wierzchołka paraboli będącej wykresem funkcji $f$ wynosi:

$p = \frac{2 + 33}{2} = 17, 5$

Wobec tego $x = 17, 5 cm$ oraz $y = (36 - 17, 5) cm = 18, 5 cm$ .

W celu zapewnienia maksymalnej powierzchni druku strona książki powinna mieć wymiary $17, 5 cm$ na $18, 5 cm$ .

Przykład 4

Obrazek ma kształt równoległoboku, w którym suma długości boku i wysokości opuszczonej na ten bok wynosi $8$ . Wyznaczymy długość tego boku i wysokości tak, aby pole tego obrazka było największe.

Rozwiązanie:

Przyjmijmy oznaczenia: $a$ - długość boku równoległoboku, $h$ - długość wysokości opuszczonej na ten bok.

Z warunków zadania mamy, że $a + h = 8$ , więc $h = 8 - a$ .

Ponieważ $a > 0$ , zatem $h \in (0, 8)$ .

Pole równoległoboku obliczamy ze wzoru $P = a h$ .

Funkcję pola w zależności od $a$ zapisujemy następująco: $f (a) = a h = a \cdot (8 - a) = - a^{2} + 8 a$ .

Wykres tej funkcji jest parabolą z ramionami skierowanymi do dołu, zatem funkcja przyjmuje wartość największą w wierzchołku paraboli, będącej jej wykresem.

Obliczamy wartość $p = \frac{- 8}{- 2} = 4$ , więc $a = 4$ i $h = 4$ .

Przykład 5

Tygodniowy popyt na pewien towar wyraża się wzorem $p (x) = 2000 - 20 x$ , gdzie $x$ oznacza cenę towaru. Wyznacz cenę, dla której dochód jest maksymalny. Obliczymy ten dochód.

Rozwiązanie:

Z warunków w zadaniu mamy, że $x > 0$ oraz $2000 - 20 x > 0$ , więc $x \in (0, 100)$ .

Funkcję dochodu możemy zapisać jako $f (x) = x \cdot p (x) = x \cdot (2000 - 20 x) = - 20 x^{2} + 2000 x$ .

Ponieważ otrzymaliśmy funkcję kwadratową, której wykres jest parabolą z ramionami skierowanymi do dołu, zatem wartość największa przyjmowana jest w wierzchołku tej paraboli.

Wyznaczamy pierwszą współrzędną wierzchołka paraboli, będącej wykresem funkcji $f$ :

$p = \frac{- 2000}{2 \cdot (- 20)} = \frac{- 2000}{- 40} = 50$ .

Otrzymujemy więc, że dla $x = 50$ dochód jest maksymalny i wynosi:

$f (50) = - 20 \cdot 50^{2} + 2000 \cdot 50 = - 50000 + 100000 = 50000$ .

Słownik

optymalizacja

metoda najlepszego rozwiązania przy uwzględnieniu zadanego warunku

ekstremum funkcji

maksymalna lub minimalna wartość funkcji

Wprowadzenie

Animacja

Słownik