Przeczytaj
Intuicyjnie każdy uczeń wie, czym jest siatka ostrosłupa. Aby jednak ujednolicić nasze wyobrażenia, rozstrzygnąć ewentualne wątpliwości, przyjmijmy następującą definicję:
Siatką ostrosłupa nazywamy rysunek płaski odzwierciedlający w rzeczywistych wymiarach ściany ostrosłupa, zawierający największą możliwą liczbę wspólnych krawędzi bryły.
Siatki ostrosłupów mogą być projektowane na różne sposoby - najczęściej rozcina się wszystkie krawędzie boczne.
W poniższym aplecie zwróć uwagę na liczbę krawędzi i wierzchołków bryły w przestrzeni oraz liczbę odcinków i wierzchołków trójkątów ścian bocznych w siatce.
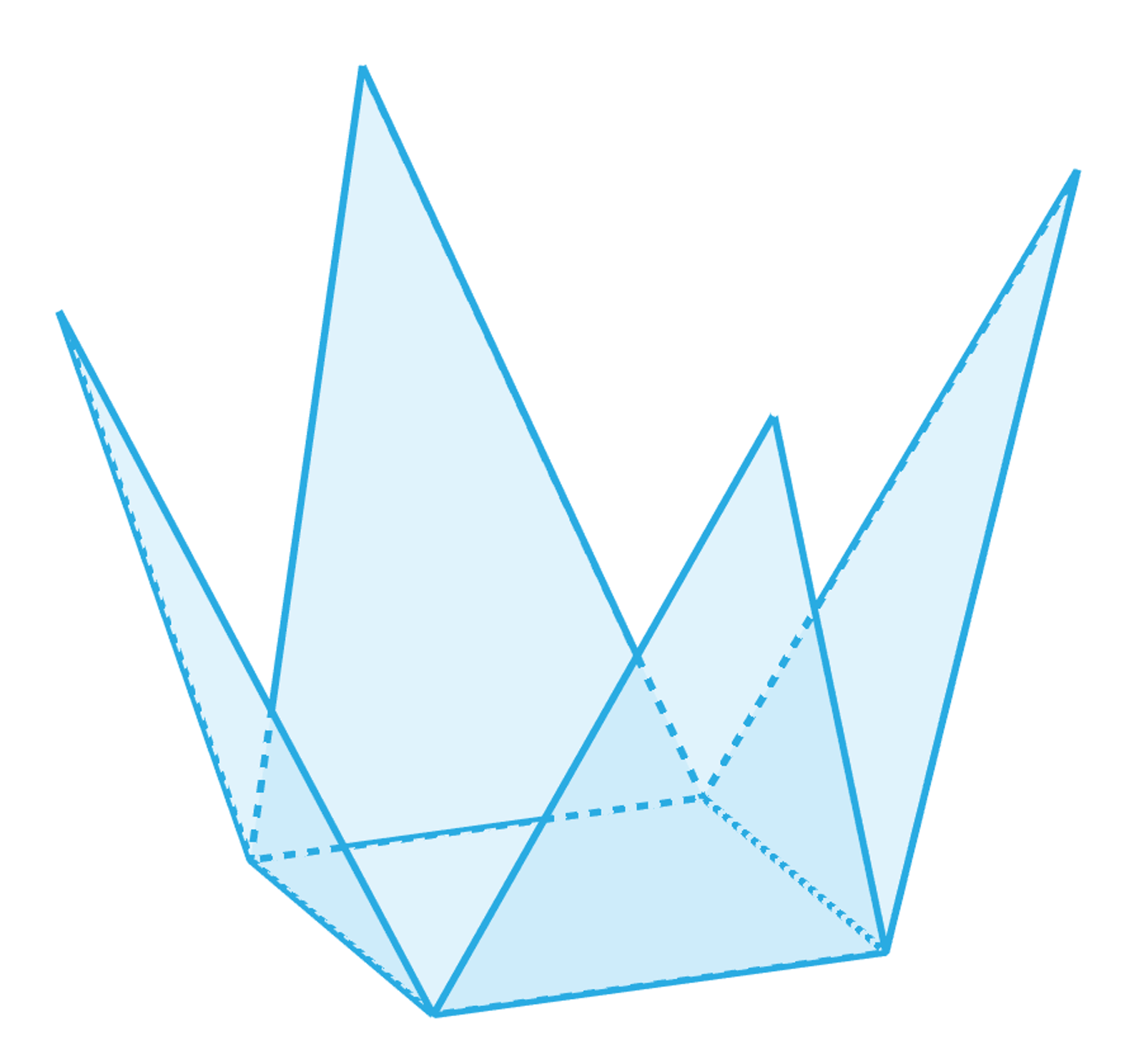
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DdeRiAl33
Aby zaprojektować siatkę ostrosłupa, musisz dobrze znać wszystkie wymiary jego ścian. Jest to zatem typowe zadanie konstrukcyjne. Przedstawiając rozwiązanie zadania konstrukcyjnego, powinniśmy wyodrębnić jego cztery etapy:
Analizę warunków.
Opis konstrukcji.
Właściwą konstrukcję.
Dowód poprawności konstrukcji.
Najczęściej w rzeczywistości szkolnej jednak, trzy wymienione etapy: analiza, opis i dowód poprawności konstrukcji są wykonywane ustnie. Uczeń skupia się jedynie na właściwej konstrukcji, którą kreśli za pomocą cyrkla i linijki.
Dane są dwa odcinki o długości odpowiednio oraz . Skonstruuj siatkę ostrosłupa sześciokątnego, którego podstawa jest wielokątem foremnymwielokątem foremnym o boku długości , wysokość jest równa i wszystkie krawędzie boczne są sobie równe.
Rozwiązanie:
Analiza zadania:
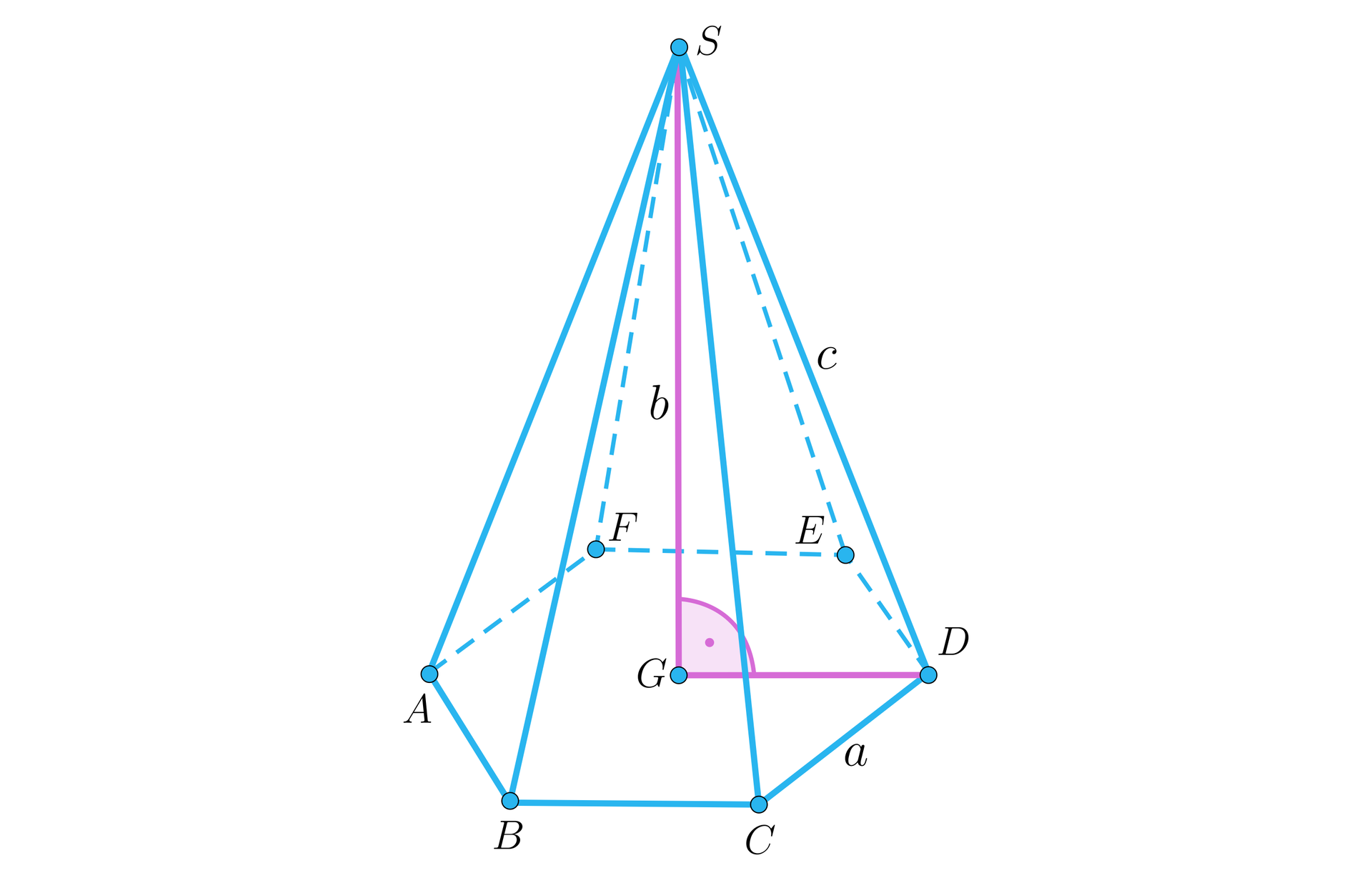
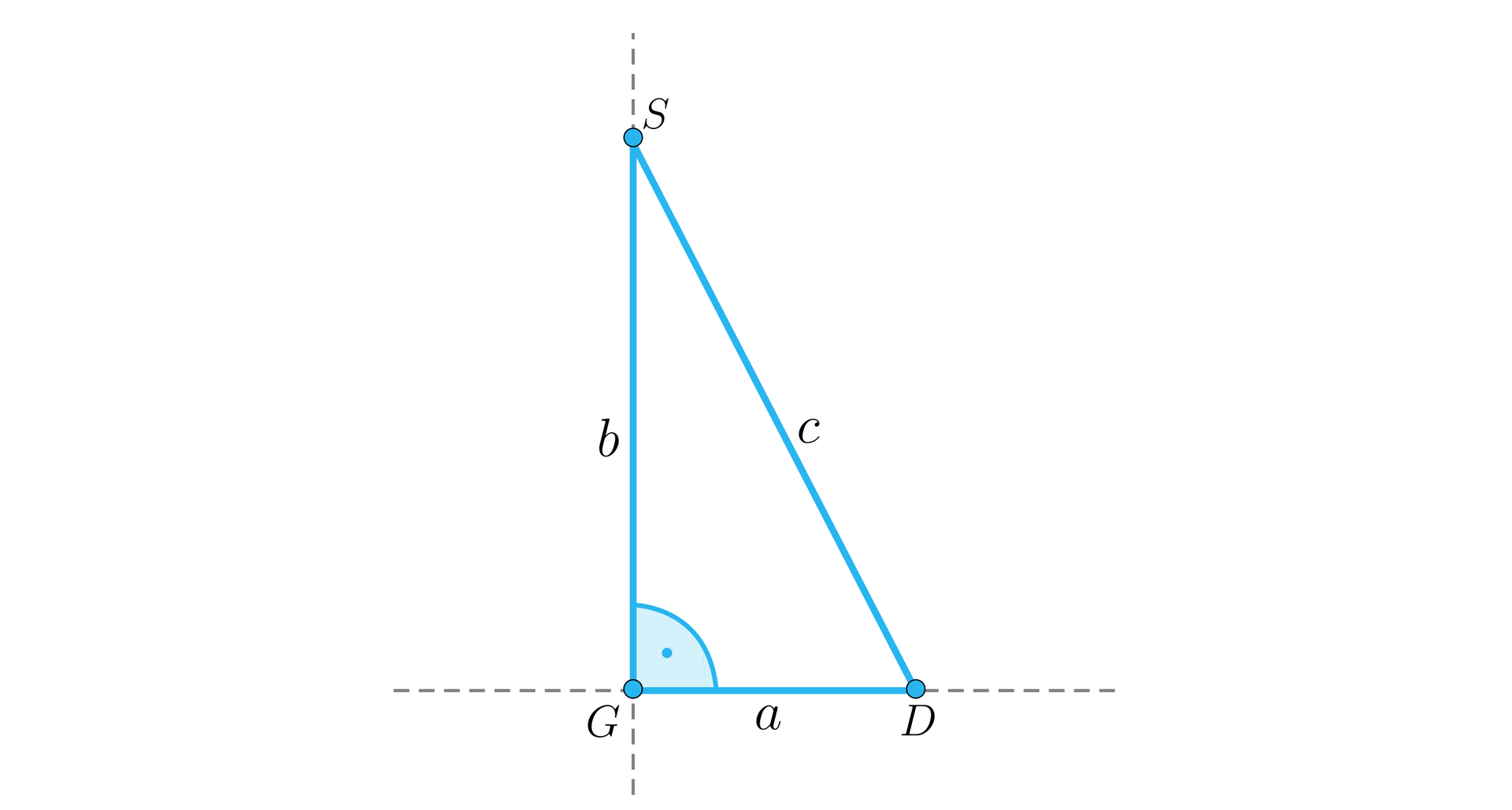
Celem zadania jest konstrukcja siatki ostrosłupa przedstawionego w rzucie. Jeżeli wszystkie krawędzie boczne tego ostrosłupa są sobie równe, to spodek wysokości znajduje się w środku symetrii podstawy. Aby skonstruować siatkę, brakuje nam odcinka , który reprezentuje krawędź boczną ostrosłupa. Konstrukcja musi zatem być dwuetapowa. W pierwszym etapie wykreślimy odcinek . W drugim etapie wykreślimy właściwą siatkę.
Opis konstrukcji:
Nr | Opis czynności | Efekt |
|---|---|---|
. | Konstruujemy trójkąt prostokątny o przyprostokątnych długości oraz . | Krawędź boczna ostrosłupa. |
. | Kreślimy sześciokąt foremny o boku długości . | Podstawa ostrosłupa. |
. | Kreślimy okręgi o środkach w wierzchołkach sześciokąta i promieniach . | Punkty siatki ostrosłupa |
. | Kreślimy trójkąty ścian bocznych. | Siatka ostrosłupa. |
Zauważmy, że w opisie konstrukcji nie trzeba podawać wszystkich czynności konstrukcyjnych. Na tym etapie nauki możemy wykorzystywać poznane wcześniej konstrukcje podstawowe, jako etapy nowych konstrukcji.
Właściwa konstrukcja:
Pierwszy etap:
Drugi etap:
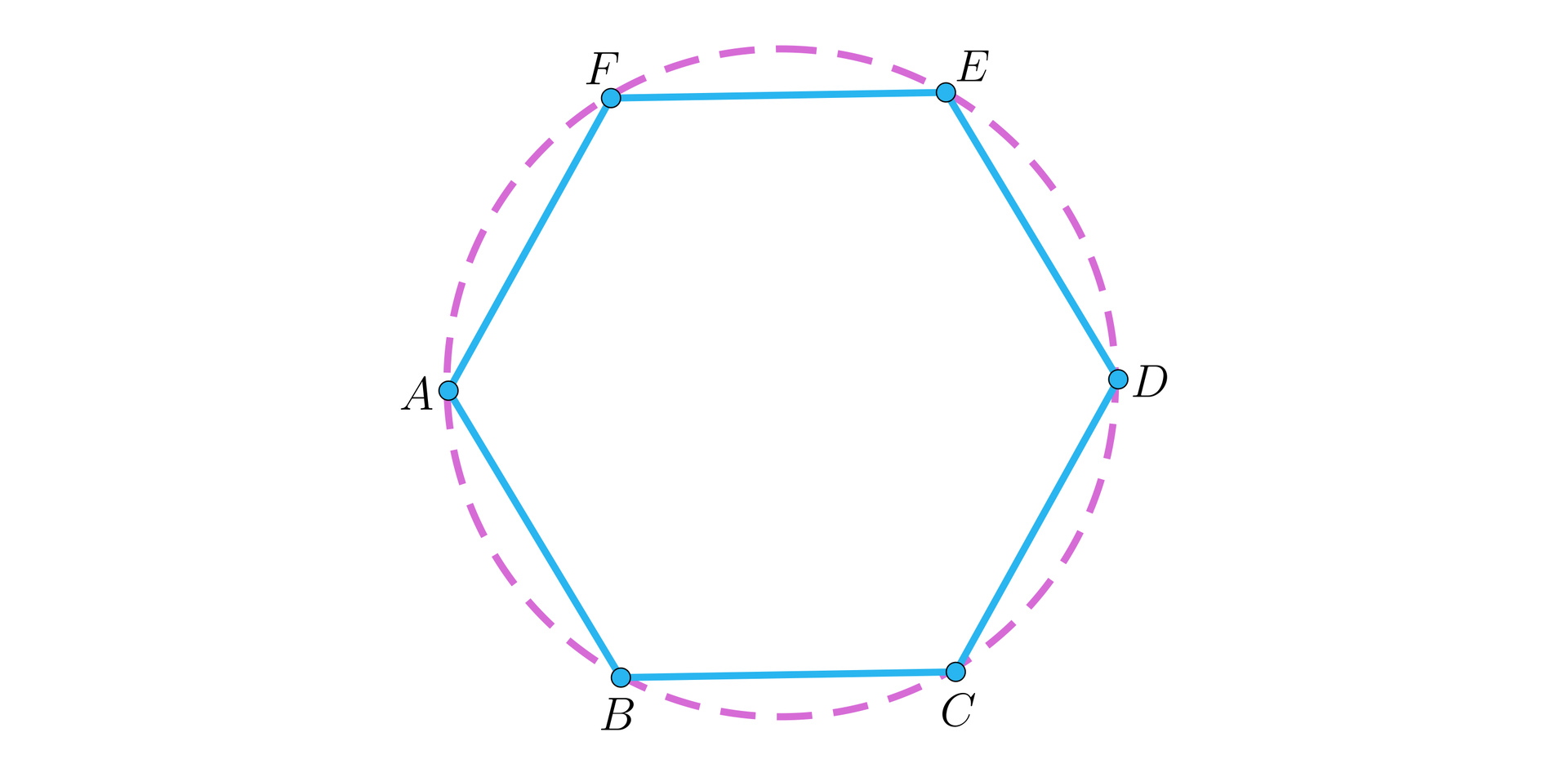

W praktyce, zamiast rysować pełne okręgi można zaznaczać tylko te ich fragmenty (łuki), które będą potrzebne do zlokalizowania punktu przecięcia kreślonych obiektów.
Dowód poprawności konstrukcji:
Podstawa jest sześciokątem foremnym (z konstrukcji), a wszystkie ściany boczne są trójkątami równoramiennymi, ponieważ ich ramiona są promieniami izometrycznych okręgówizometrycznych okręgów. Ponadto w pierwszym etapie konstrukcji widać trójkąt , który gwarantuje, że wysokość ostrosłupa po sklejeniu siatki jest równa . Konstrukcja jest możliwa do wykonania przy dowolnych zadanych z góry długościach odcinków oraz .
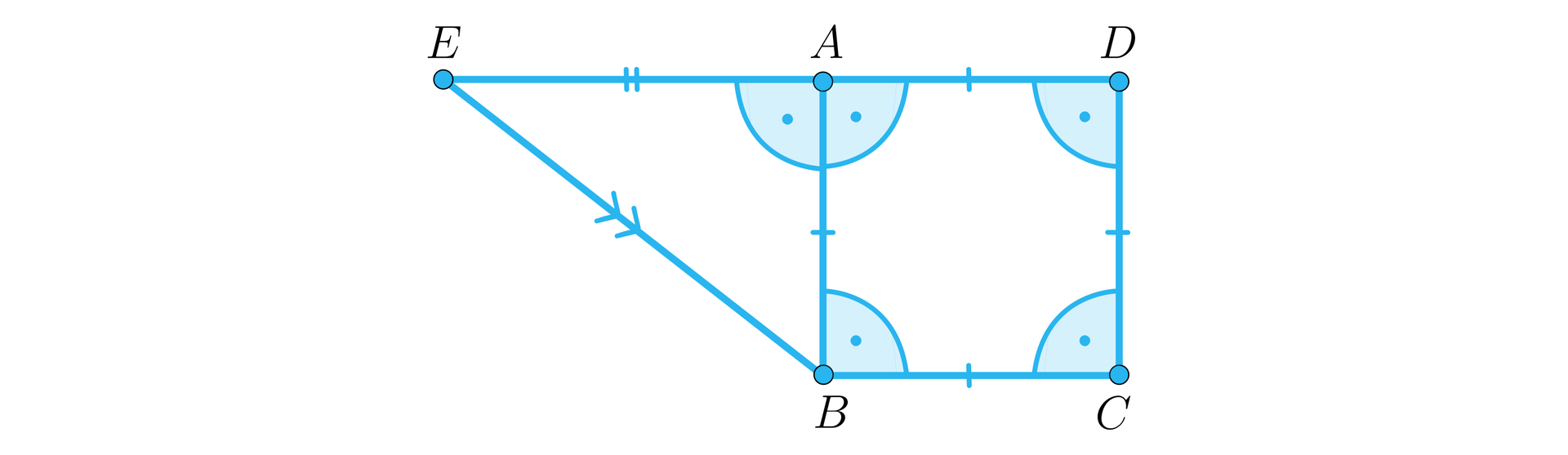
Dany jest fragment siatki ostrosłupa - jego podstawa oraz jedna ze ścian. Dokończmy tę siatkę wiedząc, że punkt jest jego spodkiem wysokości. Korzystając z siatki i informacji, że oraz obliczmy miary kątów wewnętrznych ścian bocznych danego ostrosłupa.
Rozwiązanie:
Zwróćmy uwagę na symbole umieszczone na rysunku. Jednakowymi symbolami zaznaczone są odcinki tej samej długości. Naszą bryłą jest zatem ostrosłup, którego podstawą jest kwadrat a wysokością jest krawędź . Wykonujemy odpowiedni szkic do zadania w rzucie:
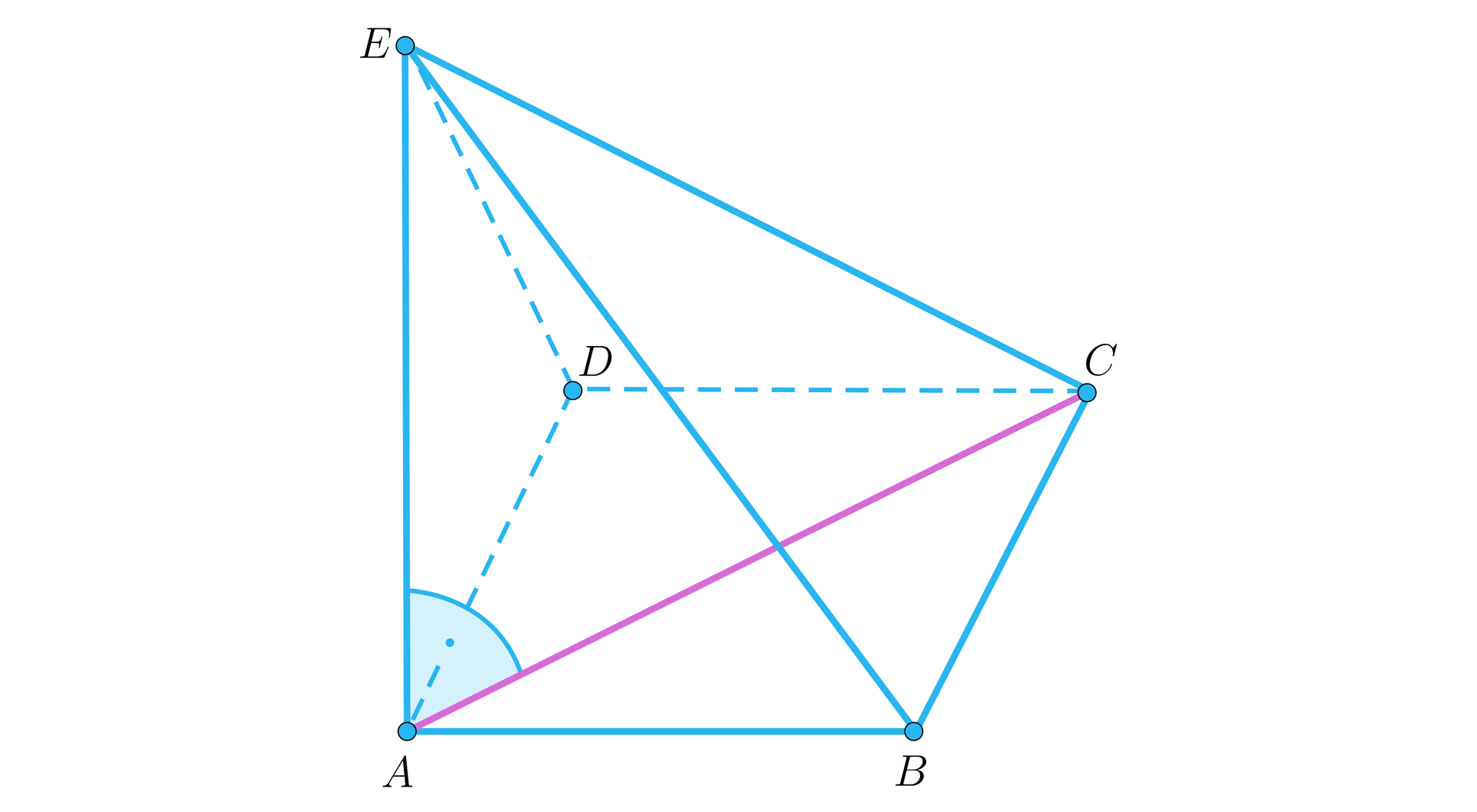
Nietrudno zauważyć, że ściany boczne tego ostrosłupa są trójkątami prostokątnymi. Trójkąty oraz mają kąt prosty przy wierzchołku . Trójkąty i są prostokątne, a krawędź jest ich przeciwprostokątną. Możemy zatem zaprojektować siatkę ostrosłupa, wystawiając w punktach , oraz odpowiednie proste prostopadłe.

Zauważmy, że dokładność konstrukcji możemy sprawdzić mierząc cyrklem odcinki o końcu . Mają one obrazować tę samą krawędź, zatem muszą być sobie równe. Jednocześnie istotnym jest, że trójkąty oraz są przystające, analogicznie trójkąty oraz .
Obliczymy teraz miary kątów wewnętrznych ścian bocznych naszego ostrosłupa. Zastosujemy definicje funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym. Wykorzystując definicję tangensa kąta ostrego w trójkącie otrzymamy:
Zatem kąty wewnętrzne trójkątów oraz to , , .
Aby wykorzystać funkcje trygonometryczne w trójkącie musimy najpierw obliczyć długość odcinka . Z twierdzenia Pitagorasa w trójkącie otrzymujemy:
Konsekwentnie zatem wyliczamy miary kątów w trójkącie :
Zatem kąty wewnętrzne trójkątów oraz to , , .
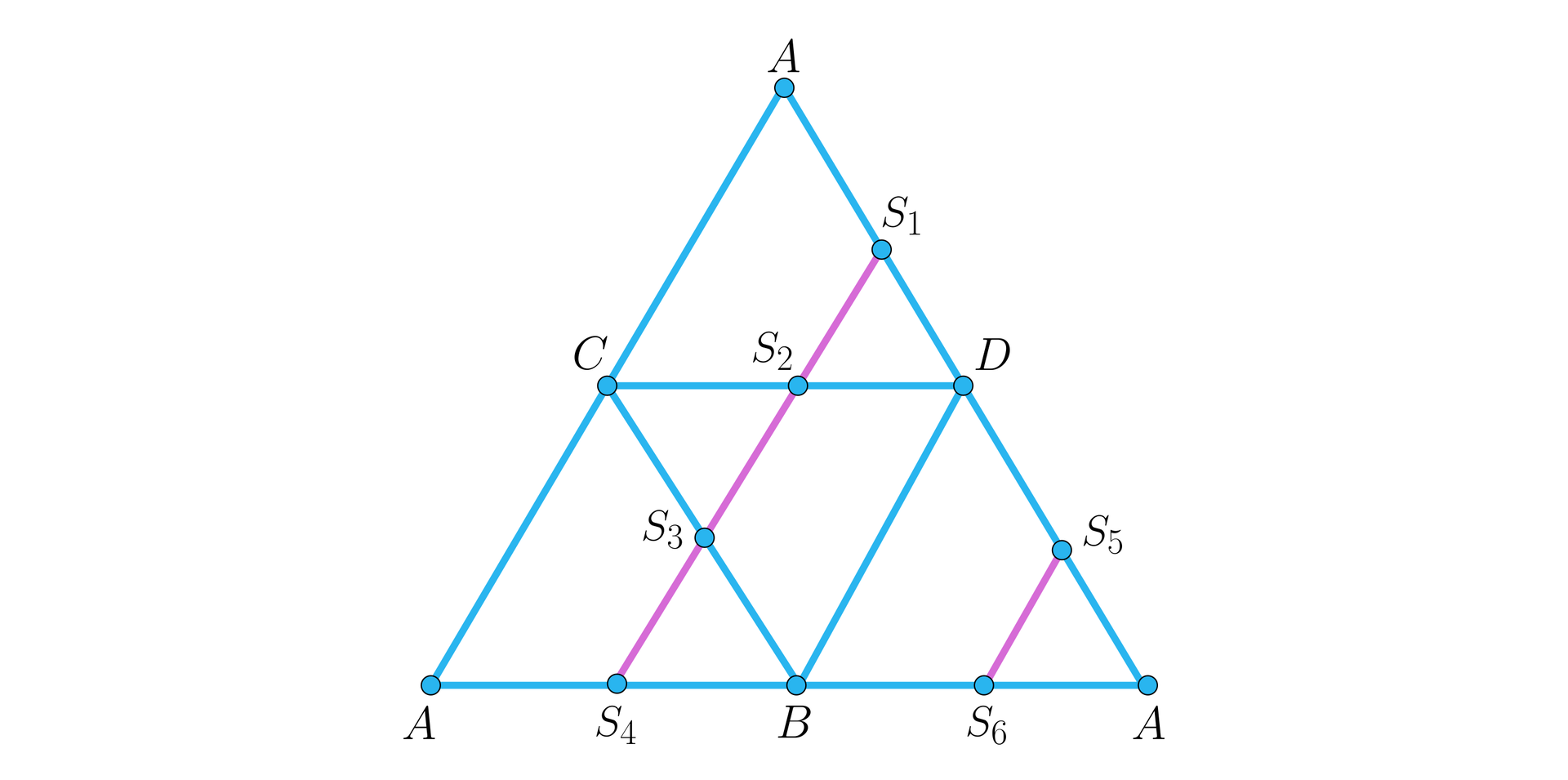
Na rysunku przestawiona jest siatka pewnego ostrosłupa, którego wszystkie krawędzie mają długość . Narysowano na niej kolorowe odcinki, których końce są każdorazowo środkami odpowiednich boków trójkątów równobocznych. Kolorowe odcinki po sklejeniu siatki w ostrosłup ograniczą pewien wielokąt. Oblicz pole tego wielokąta.
Rozwiązanie:
Po pierwsze zauważmy, że siatka zbudowana jest z czterech identycznych trójkątów równobocznych. Ostrosłupem, którego tyczy zadanie jest więc ostrosłup trójkątny. Analizując, które punkty z siatki skleją się ze sobą w przestrzeni, możemy wykonać szkic czworościanu w rzucie, który pozwoli nam zobaczyć wielokąt opisany w zadaniu.
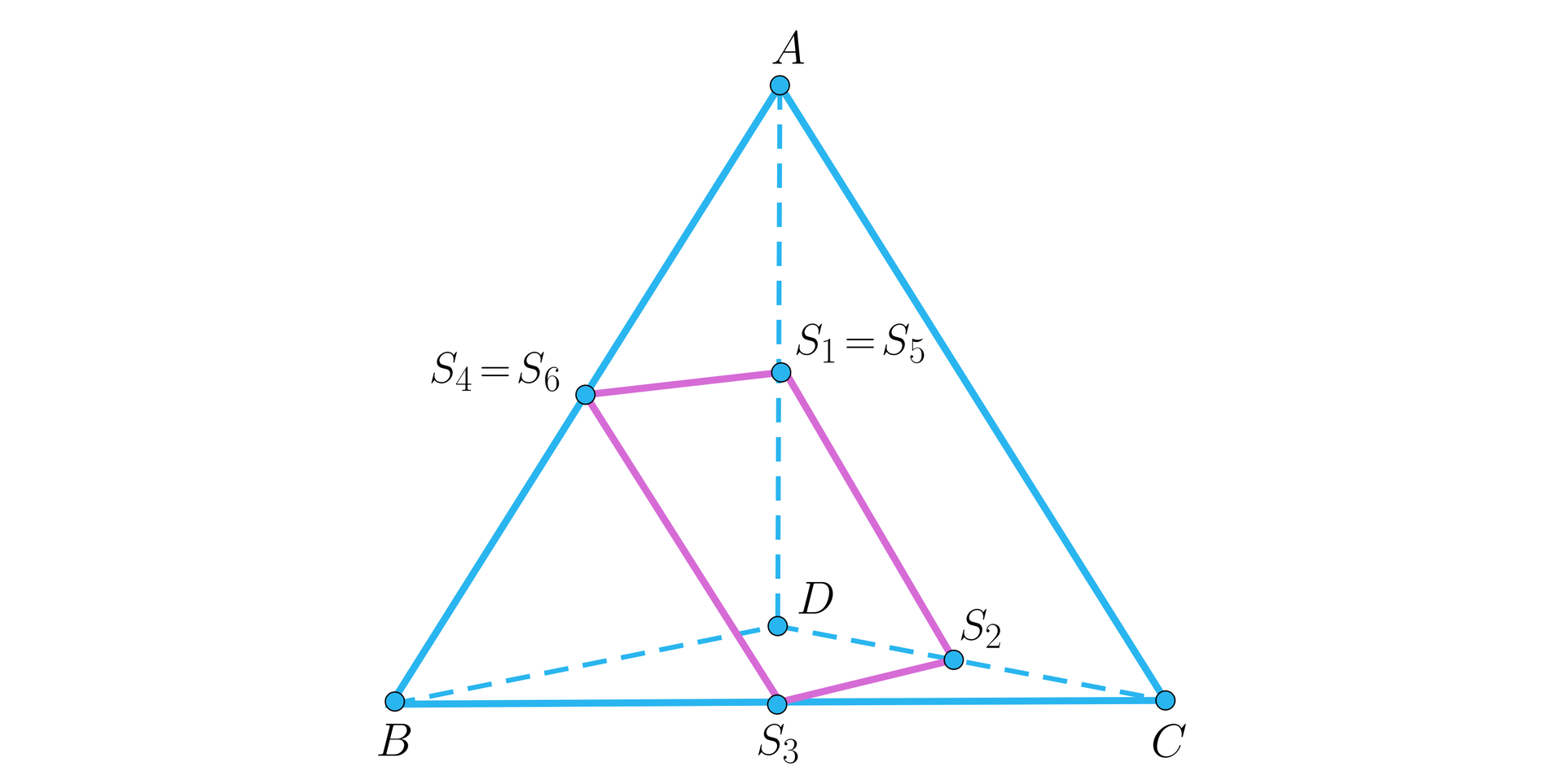
Na rysunku zaznaczona jest informacja, że punkty oraz zostały ze sobą utożsamione, analogicznie punkty oraz . Ostatecznie rozpatrujemy czworokąt . Aby obliczyć jego pole, musimy go sklasyfikować. W pierwszym etapie zauważmy, że wszystkie boki tego czworokąta są odcinkami, które łączą środki dwóch boków w trójkącie. Zgodnie z twierdzeniem odcinki te są równe zatem połowie długości trzeciego boku trójkąta, czyli w naszym przypadku . Wiemy teraz, że nasz czworokąt jest rombem.
Zauważmy teraz, że trójkąty oraz są przystające na mocy znanej nam cechy przystawania trójkątówcechy przystawania trójkątów bok - kąt - bok. Istotnie, dwa sąsiednie boki trójkątów to odpowiednio wysokość ściany bocznej i połowa krawędzi bocznej naszego ostrosłupa. Jednocześnie kąt między tymi bokami w obu trójkątach jest identyczny ze względu na symetrię naszego czworościanu. Oznacza to, że omawiany czworokąt jest rombem o przekątnych równej długości, zatem jest kwadratem. To pozwala już obliczyć pole czworokąta i rozwiązuje problem zadania.
Zauważmy, że tym razem kluczowym elementem rozwiązania zadania było wykorzystanie naszej wyobraźni przestrzennej, która pozwoliła przeanalizować własności bryły na podstawie jej siatki. Taka umiejętność rozumienia i interpretacji pojęcia matematycznego oraz operowania obiektami matematycznymi jest zapisanym w podstawie programowej wymaganiem ogólnym i jeszcze wielokrotnie będzie wykorzystywana na zajęciach. Warto ją zatem trenować.
Słownik
wielokąt, którego wszystkie boki są równej długości i wszystkie kąty wewnętrzne są równej miary
okręgi, dla których istnieje takie przekształcenie zachowujące długości boków (izometria), w którym obrazem jednego okręgu jest drugi okrąg. Warunkiem koniecznym i wystarczającym na to, by dwa okręgi były izometryczne jest równość promieni tych okręgów
twierdzenie, które wskazuje, ile minimalnie i które elementy trójkąta należy ze sobą porównać, aby udowodnić, że dane dwa trójkąty są przystające:
(a) cecha bok‑bok‑bok – przystawanie odpowiednich boków,
(b) cecha bok‑kąt‑bok – przystawanie dwóch boków i kąta między nimi,
(c) cecha kąt‑bok‑kąt – przystawanie dwóch kątów i boku zawartego w ich wspólnym ramieniu,
(d) cecha bok‑bok‑kąt – przystawanie dwóch boków i kąta naprzeciw dłuższego z nich,
(e) cecha bok‑kąt‑kąt – przystawanie dwóch kątów i boku leżącego naprzeciw wskazanego spośród nich