Równanie okręgu

Okrąg jest zbiorem punktów leżących w tej samej odległości od danego punktu, zwanego środkiem okręgu.

Rch5LjXAK5hhN

Grafika przedstawia pionową oś x oraz poziomą oś y. Na płaszczyźnie, w pierwszej ćwiartce znajduje się okrąg. Środek okręgu zaznaczono punktem C o współrzędnych: początek nawiasu, a, b, zamknięcie nawiasu. Współrzędne zostały zrzutowane na osie za pomocą przerywanych linii. Punkt a na oś x, natomiast punkt b na oś y. Okrąg przechodzi przez punkt P o współrzędnych początek nawiasu, x, y, zamknięcie nawiasu. Współrzędne tego punktu również zostały zrzutowane na osie. Punkt x na oś x, natomiast punkt y na oś y. Punkt C został połączony z punktem P linią ciągłą.

Oznaczając współrzędne środka $C$ okręgu przez $\left(a, b\right)$ a promień przez $r$, jego równanie na płaszczyźnie kartezjańskiej możemy zapisać w postaci kanonicznej:

Równanie to możemy zapisać również w innej postaci:

Podstawiając:

otrzymujemy równanie w postaci ogólnej:

Równanie to jest równaniem okręgu wtedy i tylko wtedy, gdy:

Współrzędne środka okręgu $C$ i długość promienia $r$ wyznaczamy ze wzorów:

Prosta styczna do okręgu

Przypomnijmy, że prostą nazywamy styczną do okręgu, jeśli ma z nim dokładnie $1$ punkt wspólny. Punkt wspólny nazywamy punktem styczności.

Dany jest punkt $P=\left(x_0, y_0\right)$ oraz okrąg o równaniu:

Ilość stycznych do okręgu przechodzących przez punkt $P$ zależy od wzajemnego położenia okręgu i punktu $P$. Może zachodzić jeden z trzech następujących przypadków:

1. punkt $P$ leży na zewnątrz okręgu;

   RxO2CCjiEnpfw

   Grafika przedstawia pionową oś x oraz poziomą oś y. Środek układu współrzędnych zaznaczono literą O. Na płaszczyźnie, w pierwszej ćwiartce znajduje się okrąg. Na okręgu zaznaczono dwa punkty. Przez każdy z punktów poprowadzono ukośną prostą, która jest styczna do okręgu. Jedną z nich podpisano $t_1$, a drugą $t_2$. Proste przecinaj się w punkcie, który podpisano literą P.

   

   Przez punkt $P$ przechodzą dokładnie $2$ proste styczne do tego okręgu.

2. punkt $P$ leży na okręgu;

   R3Y8krdd6Xlnn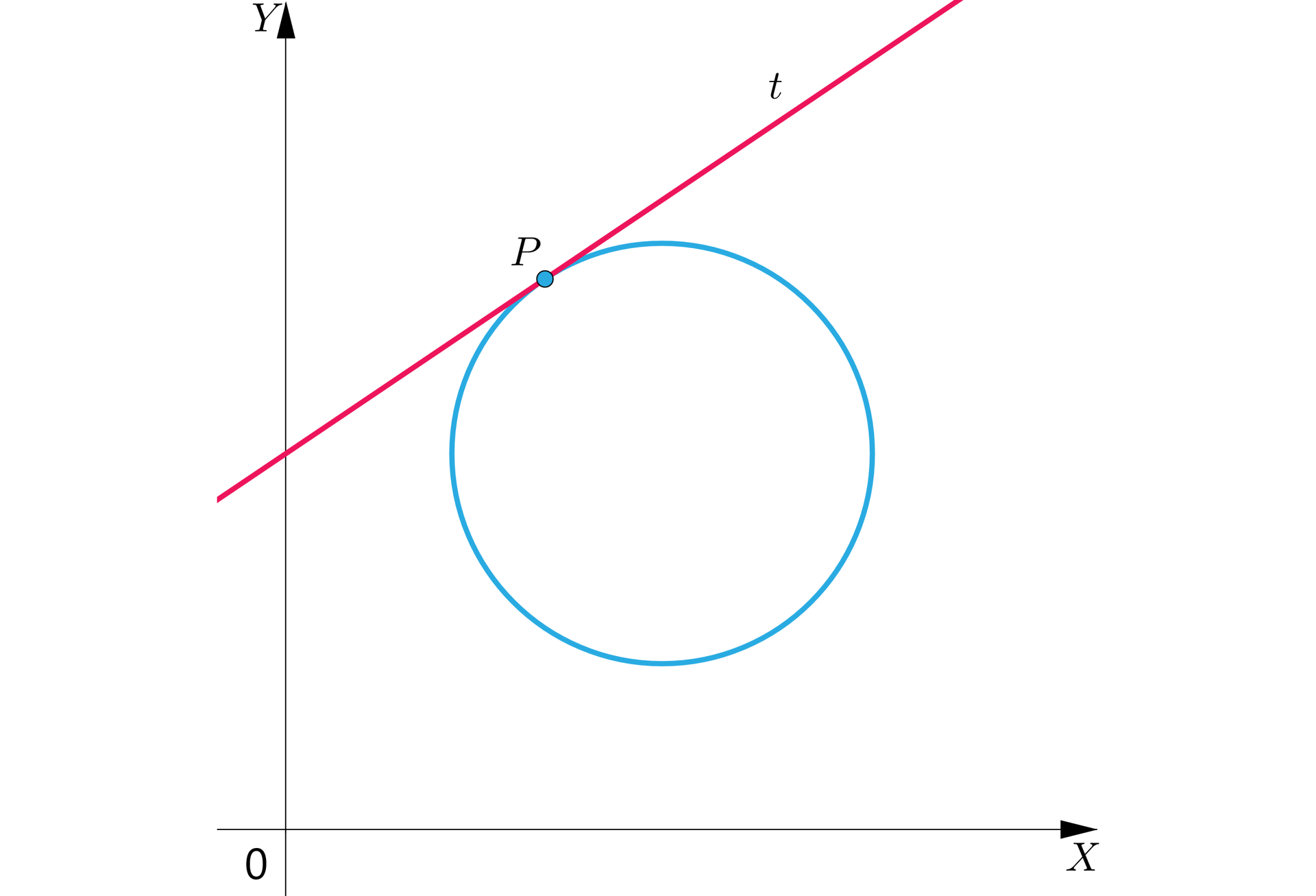

   Grafika przedstawia pionową oś x oraz poziomą oś y. Środek układu współrzędnych zaznaczono literą O. Na płaszczyźnie, w pierwszej ćwiartce znajduje się okrąg. Na okręgu zaznaczono punkt P. Przez ten punkt poprowadzono ukośną prostą, która jest styczna do okręgu. Prostą tą podpisano literą t.

   

   Przez punkt $P$ przechodzi dokładnie $1$ prosta styczna do tego okręgu. Punkt $P$ jest jednocześnie punktem styczności.

3. punkt $P$ leży wewnątrz okręgu;

   Rvx9beh94gGDV

   Grafika przedstawia pionową oś x oraz poziomą oś y. Środek układu współrzędnych zaznaczono literą O. Na płaszczyźnie, w pierwszej ćwiartce znajduje się okrąg. Wewnątrz okręgu zaznaczono punkt P.

   

   Przez punkt $P$ nie przechodzi żadna prosta styczna do tego okręgu.

Aby, w przypadkach $1$ i $2$, wyznaczyć równania stycznych do okręgu, na których leży punkt $P$, postępujemy zgodnie z poniższym algorytmem:

• Wyznaczamy współrzędne środka $C$ okręgu i długość promienia okręgu.

• Piszemy równanie pęku prostychpęk prostychpęku prostych o środku $P$ w postaci ogólnej:

  $y-y_0=m\left(x-x_0\right)$
  $mx-y+y_0-m{x}_0=0$.

• Stosujemy wzór na odległość punktu $P=\left(x_0;y_0\right)$ od prostej danej równaniem ogólnym $Ax+By+C=0$odległość punktu od prostejodległość punktu $P=\left(x_0;y_0\right)$ od prostej danej równaniem ogólnym $Ax+By+C=0$:

  $d=\frac{\left|A{x}_0+B{y}_0+C\right|}{\sqrt{A^2+B^2}}$.

• Obliczoną odległość przyrównujemy do długości promienia.

• Podstawiamy obliczone wartości $m$ do równania pęku prostych.

Przykład 3

Wyznaczymy równania stycznych do okręgu o równaniu $x^2+y^2-2x=0$ przechodzących przez punkt $P=\left(\frac{9}{4}, 0\right)$.

Rozwiązanie

Wyznaczamy współrzędne środka $C$ okręgu i długość jego promienia:

$C=\left(1, 0\right)$, $r=1$.

Piszemy równanie pęku prostych o środku $P$:

$y-0=m\left(x-\frac{9}{4}\right)$

$4mx-4y-9m=0$.

Obliczamy odległość prostych od punktu $C$:

$d=\frac{\left|4m·1-4·0-9m\right|}{\sqrt{16m^2+16}}=\frac{\left|-5m\right|}{\sqrt{16m^2+16}}$.

Przyrównujemy tak obliczoną odległość do długości promienia:

$\frac{\left|-5m\right|}{\sqrt{16m^2+16}}=1$

$\left|-5m\right|=\sqrt{16m^2+16}$.

Podnosimy obie strony do kwadratu:

$25m^2-16m^2=16$

$9m^2=16$

$m^2=\frac{16}{9}$, zatem: $m=-\frac{4}{3}$ lub $m=\frac{4}{3}$.

Podstawiamy obliczone wartości $m$ do równania pęku i otrzymujemy równania stycznych:

$t_1: y=\frac{4}{3}x-3$,

$t_2: y=-\frac{4}{3}x+3$.

R1LK2NYwyO3Qa

Grafika przedstawia pionową oś x od minus dwóch do siedmiu i pionową oś y od minus czterech do pięciu. Na płaszczyźnie zaznaczono okrąg oraz dwie ukośne proste. Środek okręgu znajduje się w punkcie początek nawiasu, 1, 0, zamknięcie nawiasu, punkt ten podpisano literą C. Okrąg ma promień o długości jeden. Na osi x w punkcie początek nawiasu $\frac{9}{4}$, 0, zamknięcie nawiasu został zaznaczony punkt P. Przez ten punkt poprowadzone zostały dwie styczne do okręgu o środku w punkcie C. Jedną styczną podpisano $t_1$ a drugą styczną podpisano $t_2$. Pierwsza styczna ma równanie $y=\frac{4}{3}x-3$ i przechodzi przecina oś y w punkcie początek nawiasu, 0, minus 3, zamknięcie nawiasu. Druga styczna ma równanie $y=-\frac{4}{3}x+3$ i przecina oś y w punkcie początek nawiasu, 0, 3, zamknięcie nawiasu

Jeśli punkt $P$ jest punktem okręgu, to poza metodami zaprezentowanymi wyżej, możemy zastosować również inną metodę.

• Wyznaczamy współrzędne środka $C$ okręgu.

• Wyznaczamy współczynnik kierunkowy $m$ prostej $l$ przechodzącej przez punkty $P$ i $C$.

• Jeśli $m\ne 0$, to wyznaczamy współczynnik $m^{\text{'}}=-\frac{1}{m}$ prostej prostopadłej do prostej $l$.

• Piszemy równanie stycznej:

  $y-y_0=m^{\text{'}}\left(x-x_0\right)$.

Ważne!

1. Jeśli prosta przechodząca przez punkty $P$ i $C$ jest równoległa do osi $X$, to równanie stycznej do okręgu ma postać: $x=x_0$, gdzie $x_0$ - odcięta punktu $P$.

2. Jeśli prosta przechodząca przez punkty $P$ i $C$ jest równoległa do osi $Y$, to równanie stycznej do okręgu ma postać: $y=y_0$, gdzie $y_0$ - rzędna punktu $P$.

Przykład 5

Wyznaczymy równania wspólnych stycznych do okręgów o równaniach $x^2+y^2-6x=0$ i $x^2+y^2+2x=0$.

Rozwiązanie

Dane okręgi mają środki w punktach $C_1=\left(3,0\right)$ i $C_2=\left(-1,0\right)$ oraz promienie o długościach odpowiednio $r_1=3$ i $r_2=1$.

Jeśli prosta o równaniu $ax+by+c=0$ jest wspólną styczną do tych okręgów, to jej odległość od środka pierwszego okręgu wynosi $3$, zaś od drugiego wynosi $1$.

Mamy zatem układ:

$\left\{\begin{array}{l}\frac{\left|3a+c\right|}{\sqrt{a^2+b^2}}=3\\ \frac{\left|-a+c\right|}{\sqrt{a^2+b^2}}=1\end{array}\right.$

stąd:

$\left\{\begin{array}{l}\left|3a+c\right|=3\sqrt{a^2+b^2}\\ \left|-a+c\right|=\sqrt{a^2+b^2}\end{array}\right.$.

Mnożąc obie strony drugiego równania przez $3$ i odejmując równanie drugie od równania pierwszego, otrzymujemy:

$\left|3a+c\right|-3\left|-a+c\right|=0$

co daje:

$\left|3a+c\right|=3\left|-a+c\right|$,

czyli

$3a+c=3·\left(c-a\right)$ lub $3a+c=-3·\left(c-a\right)$.

Stąd $c=3a$ lub $c=0$.

Jeśli $c=0$, to każde z równań układu redukuje się do równania $\left|a\right|=\sqrt{a^2+b^2}$. Oznacza to, że $b=0$, czyli prosta styczna ma równanie $x=0$.

Jeśli $c=3a$, to każde z równań układu redukuje się do postaci $\left|2a\right|=\sqrt{a^2+b^2}$. Oznacza to, że $b=\sqrt{3}a$ lub $b=-\sqrt{3}a$.

Wówczas dla dowolnego $a\ne 0$ otrzymujemy równania dwóch wspólnych stycznych:

$x+\sqrt{3}y+3=0$ i $x-\sqrt{3}y+3=0$,

które przecinają się w punkcie $A=\left(-3,0\right)$.

RMba3zFTGEikr

Grafika przedstawia pionową oś x od minus trzech do sześciu i pionową oś y od minus czterech do czterech. Na płaszczyźnie zaznaczono dwa okręgi oraz trzy proste. Pierwszy okrąg ma środek $C_1$ w punkcie początek nawiasu, 3, 0, zamknięcie nawiasu. Okrąg ten ma promień równy trzy. Drugi okrąg ma środek $C_2$ w punkcie początek nawiasu, minus 1, 0, zamknięcie nawiasu. Okrąg ten ma promień jeden. Okręgi mają punkt wspólny w początku układu współrzędnych. Przez ten punkt przechodzi pionowa prosta, pokrywająca się z osią y o równaniu $x=0$. Druga prosta jest styczna do obu okręgów i przechodzi przez trzecią, drugą i pierwszą ćwiartkę. Prosta ta ma równanie $x+\sqrt{3}y+3=0$. Trzecia prosta jest również styczna do obu okręgów i przechodzi przez drugą trzecią i czwartą ćwiartkę. Prosta ta ma równanie $x-\sqrt{3}y+3=0$. Druga i trzecia prosta przecinają się w punkcie A o współrzędnych początek nawiasu, minus 3, 0, zamknięcie nawiasu. Środki okręgów są połączone z punktami, w których przecinają się ze stycznymi.

Słownik