Nierównością pierwszego stopnia z dwiema niewiadomymi nazywamy każdą nierówność, którą możemy przedstawić w jednej z  postaci:

gdzie:
$a, b, c\in \mathrm{ℝ}$ i $a^2+b^2\ne 0$ ($a$ i $b$ nie mogą być jednocześnie zerami).

Wykresem nierówności pierwszego stopnia z dwiema niewiadomymi jest jedna z półpłaszczyzn (z krawędzią, jeśli nierówność jest nieostra lub bez krawędzi, jeśli nierówność jest ostra), wyznaczona przez prostą $ax+by=c$.

Narysujemy w jednym układzie współrzędnych ilustrację graficzną nierównościwykres nierówności pierwszego stopnia z dwiema niewiadomymiilustrację graficzną nierówności:

$x\ge 0$ i $y\ge 0$ i $x+y\le 4$.

Ilustracją geometryczną każdej z nierówności jest półpłaszczyzna, której krawędzią jest prosta odpowiednio o równaniu $x=0$, $y=0$ oraz $x+y=4$.

R2ZiWmYLgQi79

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do sześciu i pionową osią y od minus 4 do sześciu. Ćwiartki układu są zaznaczone na różne kolory: ćwiartka pierwsza ma kolor pomarańczowy, druga ma kolor różowy, trzecia ma kolor jasnoniebieski a czwarta żółty. Na płaszczyźnie zaznaczony został trójkąt prostokątny o wierzchołkach A, B oraz C, które oznaczono zamalowanymi punktami. Współrzędne wierzchołków są następujące: wierzchołek A: początek nawiasu, zero, zero, zamknięcie nawiasu, wierzchołek B: początek nawiasu, cztery, zero, zamknięcie nawiasu, wierzchołek C: początek nawiasu, zero, cztery, zamknięcie nawiasu. Przeciwprostokątna BC leży na prostej o równaniu $x+y=4$, natomiast oś y jest opisana równaniem $y=0$. Fragment płaszczyzny znajdujący się po lewej stronie prostej $x+y=4$ jest zaznaczony kolorem ciemnoniebieskim i podpisany $x+y\le 4$. Część ćwiartki drugiej znajdującej się poza ciemnoniebieskim obszarem jest podpisana $y\ge 0$, a część ćwiartki czwartej jest podpisana $x\ge 0$.

Nałożone na siebie półpłaszczyzny tworzą trójkąt $ABC$. Współrzędne punktów należących do tego trójkąta to pary liczb, będące rozwiązaniami układu    nierówności $\left\{\begin{array}{c}x\ge 0 \\ y\ge 0 \\ x+y\le 4\end{array}\right.$.

Układem nierówności pierwszego stopnia z dwiema niewiadomymi nazywamy koniunkcję tych nierówności.

Znajdziemy teraz zbiór rozwiązań układu nierównościukład nierówności pierwszego stopnia z dwiema niewiadomymiukładu nierówności $\left\{\begin{array}{c}2x-3y+6>0\\ 2x-3y-9<0\end{array}\right.$.

W prostokątnym układzie współrzędnych umieszczamy ilustrację graficzną każdej nierówności zapisanej w układzie.

Na poniższym rysunku kolorem różowym zaznaczono graficzną interpretację zbioru rozwiązań nierównościnierówność pierwszego stopnia z dwiema niewiadomyminierówności $2x-3y+6>0$, a kolorem niebieskim nierówności $2x-3y-9<0$. Proste ograniczające półpłaszczyzny zaznaczyliśmy linią przerywana, ponieważ nierówności są ostre.

Część płaszczyzny zaznaczona kolorem szarym jest częścią wspólną tych półpłaszczyzn, a więc interpretacją geometryczną zbioru rozwiązań układu nierówności.

RnIvVC9R2ad64

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do sześciu i pionową osią y od minus 5 do pięciu. Na płaszczyźnie znajdują się dwie proste zaznaczone linią przerywaną. Pierwsza prosta ma równanie $2x-3y+6=0$, druga prosta ma równanie $2x-3y-9=0$. Obszar znajdujący się nad pierwszą prostą ma kolor niebieski i jest podpisany $2x-3y-9<0$, obszar pomiędzy prostymi jest zaznaczony kolorem fioletowym, obszar pod drugą prostą ma kolor różowy i jest podpisany $2x-3y+6>0$.

A zatem ilustracją geometryczną rozwiązania układu nierówności $\left\{\begin{array}{c}2x-3y+6>0\\ 2x-3y-9<0\end{array}\right.$ jest zbiór wszystkich punktów przedstawionych na rysunku.

R98HTgFjkejAT

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do sześciu i pionową osią y od minus 5 do pięciu. Na płaszczyźnie znajdują się dwie proste zaznaczone linią przerywaną. Pierwsza prosta ma równanie $2x-3y+6=0$, druga prosta ma równanie $2x-3y-9=0$. Obszar znajdujący się pomiędzy prostymi został zaciemniony.

Zapiszemy układ nierówności, który opisuje zbiór punktów przedstawiony na rysunku.

RZR4HzwwDhJ2h

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do sześciu i pionową osią y od minus 3 do sześciu. Na płaszczyźnie zaznaczony został czworokąt o wierzchołkach A, B, C oraz D, które oznaczono zamalowanymi punktami. Współrzędne wierzchołków są następujące: wierzchołek A początek nawiasu, 3, 4, zamknięcie nawiasu, wierzchołek B początek nawiasu, minus 4, 2, zamknięcie nawiasu, wierzchołek C początek nawiasu, minus 2, minus 2, zamknięcie nawiasu, wierzchołek D początek nawiasu, 6, minus 1, zamknięcie nawiasu. Boki czworokąta są opisane następującymi równaniami: Bok BA $3x-7y+26=0$, bok AD $2x+y-11=0$, bok CD $x-8y-14=0$, bok BC $2x+y+6=0$.

Z rysunku odczytujemy informacje:

• przedstawiony obszar jest częścią wspólną czterech półpłaszczyzn,

• każda z tych półpłaszczyzn jest ilustracją graficzną nierówności pierwszego stopnia z dwiema niewiadomymi,

• każda z tych nierówności jest nierównością nieostrą, ponieważ proste ograniczające figurę są narysowane linią ciągłą.

Pierwsza z półpłaszczyzn znajduje się poniżej prostej $AB$.

Doprowadzamy prostą $AB$ do postaci kierunkowej $y=ax+b$:

$3x-7y+26=0$

$-7y=-3x-26 \left|:\left(-7\right)\right.$

$y=\frac{3}{7}x+\frac{26}{7}$

Jest więc półpłaszczyzną określoną nierównością

$y\le \frac{3}{7}x+\frac{26}{7}$.

Możemy tę nierówność zapisać w postaci ogólnej:

$y\le \frac{3}{7}x+\frac{26}{7} \left|·7\right.$

$7y\le 3x+26$

$-3x+7y-26\le 0 \left|:\left(-1\right)\right.$

$3x-7y+26\ge 0$

Postępując analogicznie otrzymujemy półpłaszczyzny wyznaczone przez:

• prostą $AD$:
  $y\le -2x+11$
  lub
  $2x+y-11\le 0$,

• prostą $CD$:
  $y\ge \frac{1}{8}x-\frac{14}{8}$
  lub
  $x-8y-14\le 0$,

• prostą $CB$:
  $y\ge -2x-6$
  lub
  $2x+y+6\ge 0$.

A zatem przedstawiony na rysunku obszar możemy zapisać za pomocą układu nierówności

$\{\begin{array}{l}y\le \frac{3}{7}x+\frac{26}{7}\\ y\le -2x+11\\ y\ge \frac{1}{8}x-\frac{14}{8}\\ y\ge -2x-6\end{array}$

lub za pomocą układu równoważnego

$\{\begin{array}{l}3x-7y+26\ge 0\\ 2x+y-11\le 0\\ x-8y-14\le 0\\ 2x+y+6\ge 0\end{array}$.

Za pomocą układu nierówności opiszemy trójkąt $ABC$, gdzie $A=\left(-2, -2\right)$, $B=\left(6, -1\right)$, $C=\left(\mathrm{2,} 5\right)$.

Rysujemy trójkąt $ABC$ w układzie współrzędnych.

RqYPTA3iSNgBG

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do ośmiu i pionową osią y od minus 4 do sześciu. Na płaszczyźnie zaznaczony został trójkąt o wierzchołkach A, B, oraz C, które oznaczono zamalowanymi punktami. Współrzędne wierzchołków są następujące: wierzchołek A początek nawiasu, minus 2, minus 2, zamknięcie nawiasu, wierzchołek B początek nawiasu, 6,minus 1, zamknięcie nawiasu, wierzchołek C początek nawiasu, 2, 5, zamknięcie nawiasu.

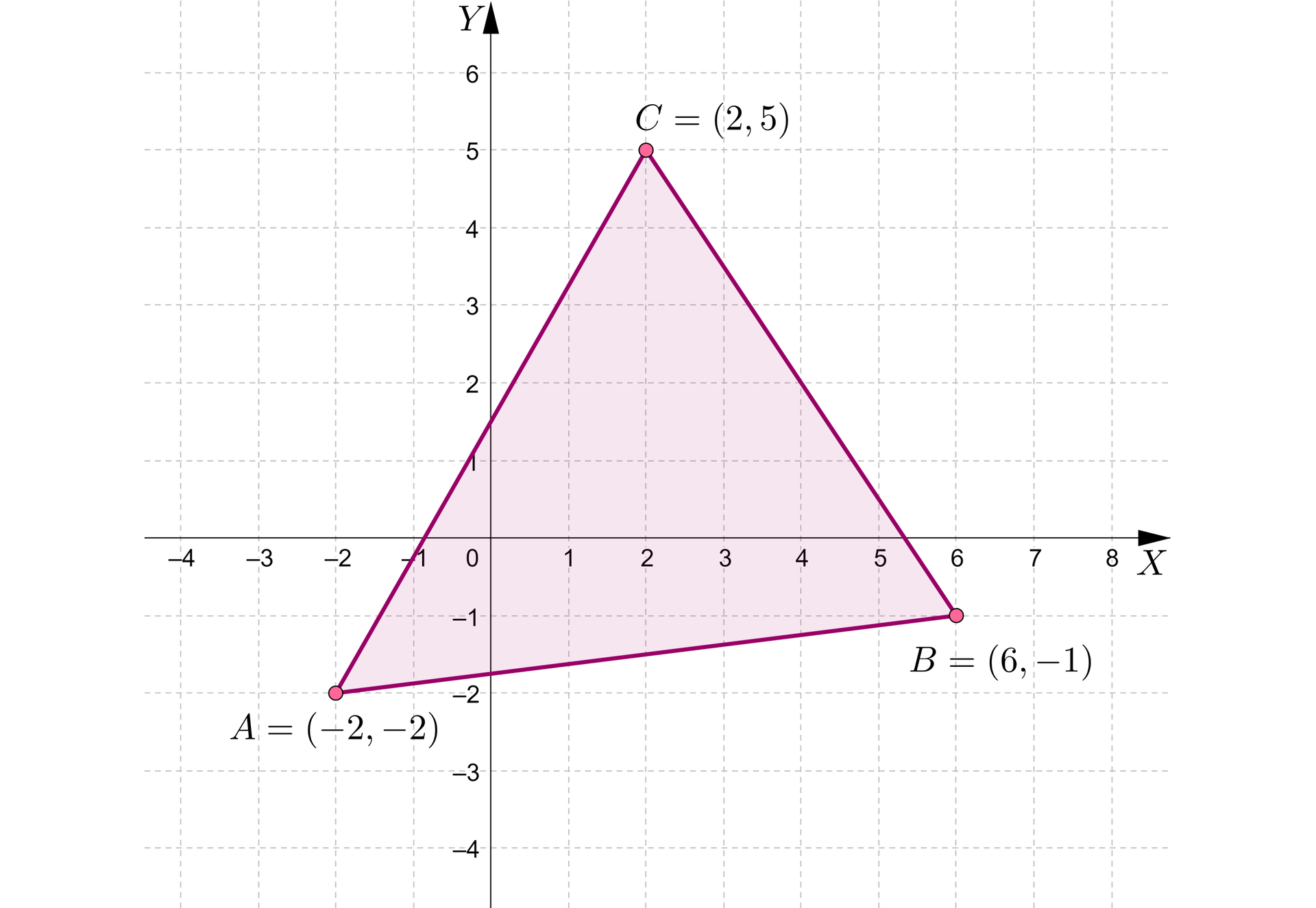
Zapisujemy równania prostych, w których zawarte są boki trójkąta.

Prosta $AB$, to prosta przechodząca przez punkty $A=\left(-2, -2\right)$ i $B=\left(6, -1\right)$.

Podstawiając współrzędne punktu $A$ do równania kierunkowego prostej $y=a_{1}x+b_1$, otrzymujemy:

$-2=-2a_1+b_1 \Rightarrow b_1=2a_1-2$.

Podstawiając współrzędne punktu $B$ do równania kierunkowego prostej $y=a_{1}x+b_1$, otrzymujemy:

$-1=6a_1+b_1\Rightarrow b_1=-6a_1-1$.

Z powyższych równań mamy:

$2a_1-2=-6a_1-1$

$8a_1=1$

$a_1=\frac{1}{8}$.

A wtedy:

$b_1=2a_1-2=-1\frac{3}{4}$.

A zatem równanie prostej $AC$ przyjmuje postać:

$y=\frac{1}{8}x-1\frac{3}{4}$.

Prosta $BC$, to prosta przechodząca przez punkty $B=\left(6, -1\right)$ i $C=\left(\mathrm{2,} 5\right)$.

Podstawiając współrzędne punktu $B$ do równania kierunkowego prostej $y=a_{2}x+b_2$, otrzymujemy:

$-1=6a_2+b_2\Rightarrow b_2=-6a_2-1$.

Podstawiając współrzędne punktu $C$ do równania kierunkowego prostej $y=a_{2}x+b_2$, otrzymujemy:

$5=2a_2+b_2\Rightarrow b_2=-2a_2+5$.

Z powyższych równań mamy:

$-6a_2-1=-2a_2+5$

$-4a_2=6$

$a_2=-\frac{3}{2}$.

A wtedy:

$b_2=-6a_2-1=8$.

A zatem równanie prostej $BC$ przyjmuje postać:

$y=-\frac{3}{2}x+8$.

Prosta $AC$, to prosta przechodząca przez punkty $A=\left(-2, -2\right)$ i $C=\left(\mathrm{2,} 5\right)$.

Podstawiając współrzędne punktu $A$ do równania kierunkowego prostej $y=a_{3}x+b_3$, otrzymujemy:

$-2=-2a_3+b_3\Rightarrow b_3=2a_3-2$.

Podstawiając współrzędne punktu $C$ do równania kierunkowego prostej $y=a_{3}x+b_3$, otrzymujemy:

$5=2a_3+b_3\Rightarrow b_3=-2a_3+5$.

Z powyższych równań mamy:

$2a_3-2=-2a_3+5$

$4a_3=7$

$a_3=\frac{7}{4}$.

A wtedy:

$b_3=2a_3-2=\frac{3}{2}$.

A zatem równanie prostej $AB$ przyjmuje postać:

$y=1\frac{3}{4}x+1\frac{1}{2}$.

R7ULkk7j8b6CK

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do ośmiu i pionową osią y od minus 4 do sześciu. Na płaszczyźnie zaznaczony został trójkąt o wierzchołkach A, B, oraz C, które oznaczono zamalowanymi punktami. Współrzędne wierzchołków są następujące: wierzchołek A początek nawiasu, minus 2, minus 2, zamknięcie nawiasu, wierzchołek B początek nawiasu, 6,minus 1, zamknięcie nawiasu, wierzchołek C początek nawiasu, 2, 5, zamknięcie nawiasu. Boki trójkąta są opisane następującymi równaniami: bok AC $y=\frac{1}{3}x+1\frac{1}{2}$, bok CB $y=-1\frac{1}{3}x+8$, bok AB $y=\frac{1}{8}x-1\frac{3}{4}$.

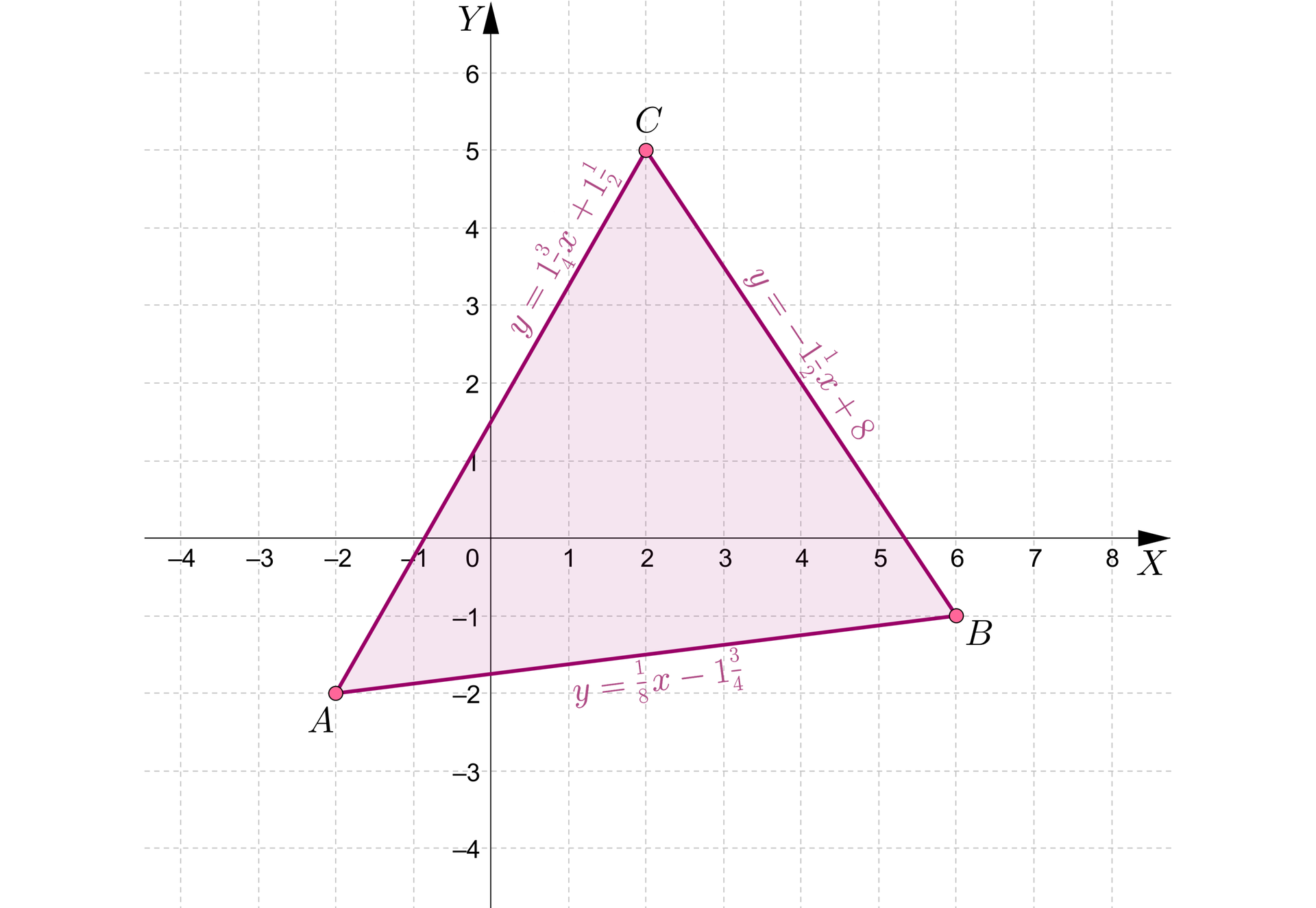
Część płaszczyzny wyznaczona przez trójkąt jest częścią wspólną półpłaszczyzn wyznaczonych przez te proste i znajdujących się odpowiednio powyżej prostej $AB$, poniżej prostej $BC$ i poniżej prostej $AC$.

A zatem możemy ją opisać za pomocą układu nierówności

$\{\begin{array}{c}y\ge \frac{1}{8}x-1\frac{3}{4}\\ y\le -\frac{3}{2}x+8\\ y\le 1\frac{3}{4}x+1\frac{1}{2}\end{array}$.

W prostokątnym układzie współrzędnych zaznaczymy zbiór punktów spełniających układ nierówności.

$\left\{\begin{array}{l}\left|x\right|+\left|y\right|<4 \\ \left|x-2\right|+1<y\end{array}\right.$

Korzystając z definicji modułu, możemy zapisać nierówność $\left|x\right|+\left|y\right|<4$ w postaci alternatywy układów nierówności:

$\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y<4\end{array}\right.$ lub $\left\{\begin{array}{l}x\ge 0\\ y<0\\ x-y<4\end{array}\right.$ lub $\left\{\begin{array}{l}x<0\\ y<0\\ -x-y<4\end{array}\right.$ lub $\left\{\begin{array}{l}x<0\\ y\ge 0\\ -x+y<4\end{array}\right.$.

Przekształcając równoważnie nierówności, otrzymujemy:

$\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ y<-x+4\end{array}\right.$ lub $\left\{\begin{array}{l}x\ge 0\\ y<0\\ y>x-4\end{array}\right.$ lub $\{\begin{array}{l}x<0\\ y<0\\ y>-x-4\end{array}$ lub $\left\{\begin{array}{l}x<0\\ y\ge 0\\ y<x+4\end{array}\right.$.

Każdy z układów nierówności przedstawiamy w jednym układzie współrzędnych.

Ry63LH13tDD31

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do sześciu i pionową osią y od minus 5 do pięciu. Na osiach zaznaczone zostały cztery następujące niezamalowane punkty: pierwszy: początek nawiasu, minus 4, 0, zamknięcie nawiasu, drugi: początek nawiasu, 0, 4, zamknięcie nawiasu, trzeci: początek nawiasu, 4, 0, zamknięcie nawiasu i czwarty: początek nawiasu, 0, minus 4, zamknięcie nawiasu. Punkty zostały połączone liniami przerywanymi, tak że na płaszczyźnie pojawił się romb. Osie dzielą romb na cztery części w kształcie trójkąta. Część znajdująca się w ćwiartce pierwszej ma kolor niebieski, część znajdująca się w ćwiartce drugiej ma kolor pomarańczowy, część z ćwiartki trzeciej ma kolor różowy, a część znajdująca się w ćwiartce czwartej ma kolor fioletowy.

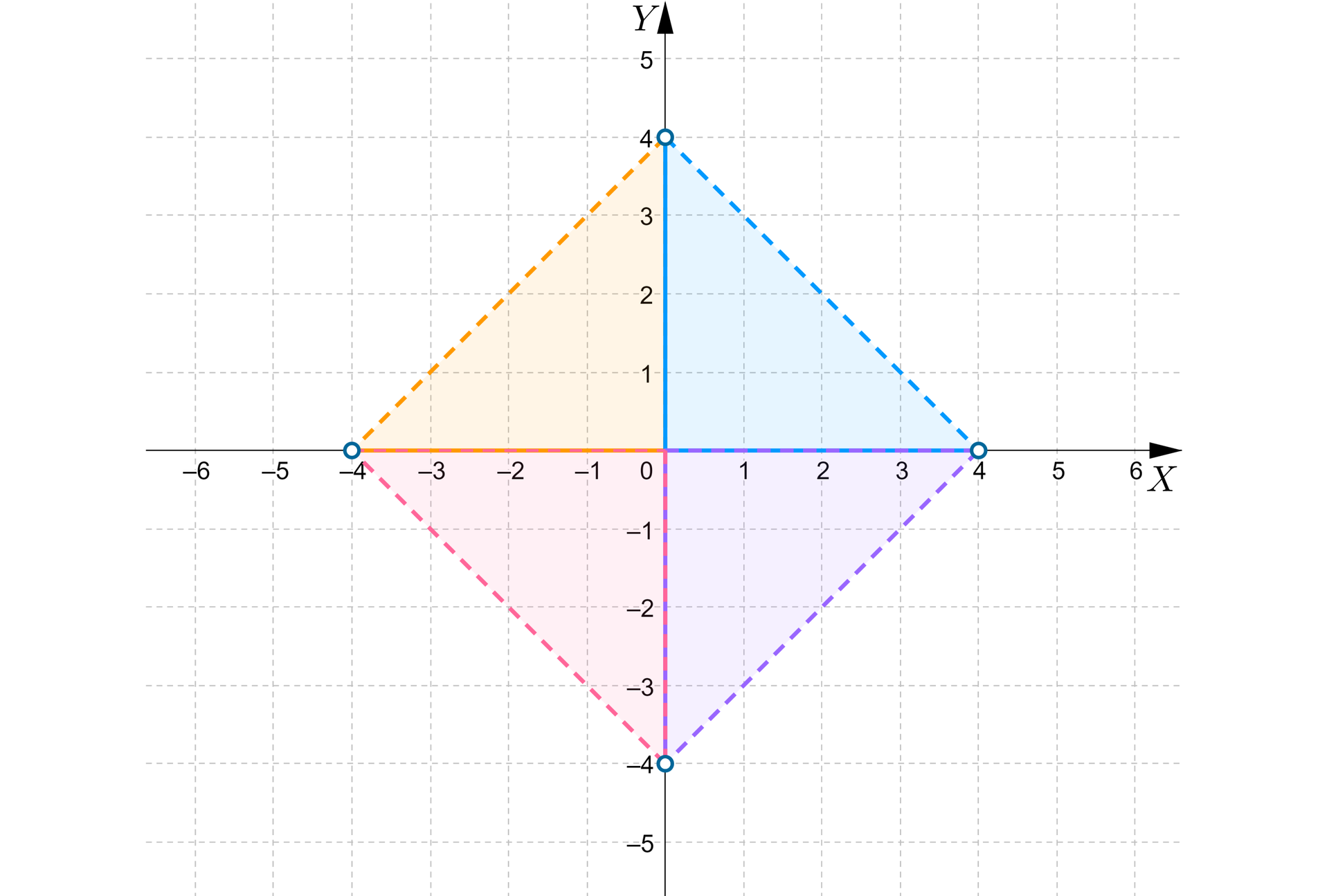
Ponieważ mamy tu alternatywę układów nierówności, więc rozwiązaniem nierówności $\left|x\right|+\left|y\right|<4$ jest suma zaznaczonych obszarów.

RhHY7cpdBv6ML

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do sześciu i pionową osią y od minus 5 do pięciu. Na osiach zaznaczone zostały cztery niezamalowane następujące punkty: pierwszy: początek nawiasu, minus 4, 0, zamknięcie nawiasu, drugi: początek nawiasu, 0, 4, zamknięcie nawiasu, trzeci: początek nawiasu, 4, 0, zamknięcie nawiasu i czwarty: początek nawiasu, 0, minus 4, zamknięcie nawiasu. Punkty zostały połączone liniami przerywanymi, tak że na płaszczyźnie znajduje się romb. Obszar wewnątrz rombu został zaznaczony kolorem niebieskim.

Rozwiążemy teraz nierówność $|x-2|+1<y$. Korzystając z definicji modułu możemy ją zapisać w postaci alternatywy układów nierówności:

$\{\begin{array}{l}x\ge 2\\ y>x-1\end{array}$ lub $\left\{\begin{array}{l}x<2\\ y>-x+3\end{array}\right.$.

A następnie przedstawimy jej interpretację graficzną.

RIM82lYLwcqQe

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do ośmiu i pionową osią y od minus 3 do sześciu. Na płaszczyć niej znajdują się trzy proste, pierwsza o równaniu $y=x+3$, druga o równaniu $y=x-1$ i trzecia o równaniu $x=2$ .Wszystkie proste przecinają się w niezamalowanym punkcie początek nawiasu, 1, 1, zamknięcie nawiasu. Pierwsza prosta biegnąc od minus nieskończoności do punktu nawiasu, 1, 1, zamknięcie nawiasu jest namalowana różową linią przerywaną, a po przekroczeniu tego punktu jest zaznaczona linią ciągłą. Druga prosta od minus nieskończoności do punktu nawiasu, 1, 1, zamknięcie nawiasu jest namalowana niebieską linią ciągłą, a po przekroczeniu tego punktu jest zaznaczona linią przerywaną. Trzecia prosta poniżej punktu nawiasu, 1, 1, zamknięcie nawiasu ma kolor szary, a powyżej niebieski. Obszar znajdujący się pomiędzy przerywaną częścią pierwszej prostej i niebieską częścią trzeciej prostej jest zaznaczony kolorem różowym. Obszar znajdujący się pomiędzy przerywaną częścią drugiej prostej i niebieską częścią trzeciej prostej jest zaznaczony kolorem niebieskim.

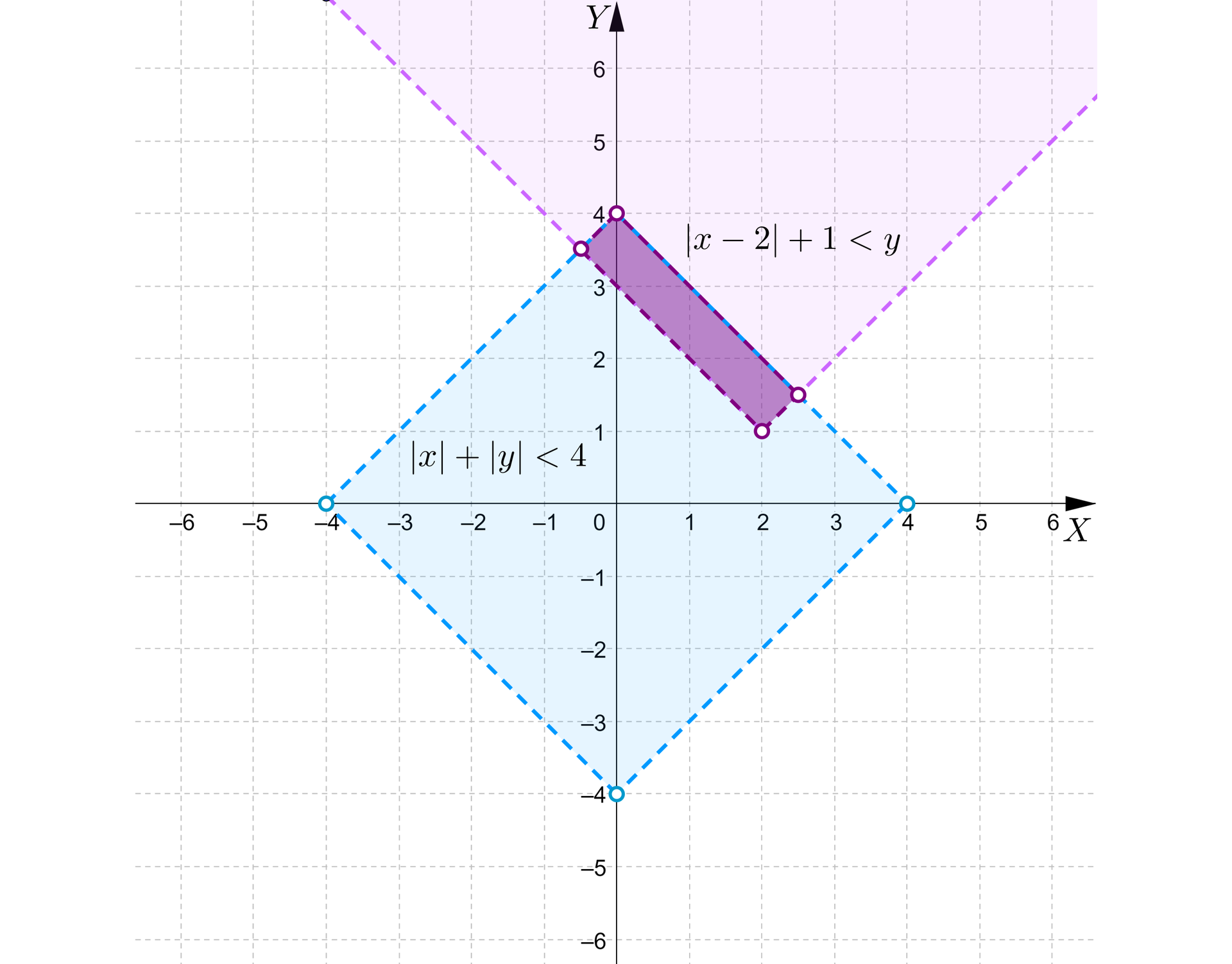
Rysujemy teraz obie nierówności w jednym układzie współrzędnych i zaznaczamy część wspólną otrzymanych zbiorów.

Iloczyn ten jest rozwiązaniem układu nierówności

$\left\{\begin{array}{l}\left|x\right|+\left|y\right|<4\\ \left|x-2\right|+1<y\end{array}\right.$.

RrZEQlqF3zuYc

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do sześciu i pionową osią y od minus 5 do pięciu. Na osiach zaznaczone zostały cztery następujące niezamalowane punkty: pierwszy: początek nawiasu, minus 4, 0, zamknięcie nawiasu, drugi: początek nawiasu, 0, 4, zamknięcie nawiasu, trzeci: początek nawiasu, 4, 0, zamknięcie nawiasu i czwarty: początek nawiasu, 0, minus 4, zamknięcie nawiasu. Punkty zostały połączone liniami przerywanymi, tak że na płaszczyźnie znajduje się romb. Obszar wewnątrz rombu został zaznaczony kolorem niebieskim i jest on podpisany $\left|x\right|+\left|y\right|<4$. Na płaszczyźnie znajdują się również dwie półproste, pierwsza przechodzi przez niezamalowane punkty początek nawiasu, minus 0,5, 3,5, zamknięcie nawiasu oraz początek nawiasu, 2, 1, zamknięcie nawiasu. Druga półprosta przechodzi przez punkty początek nawiasu, 2, 1, zamknięcie nawiasu i początek nawiasu, 2,5, 1,5, zamknięcie nawiasu. Obszar pomiędzy półprostymi zaznaczono na kolor fioletowy i podpisano $\left|x-2\right|+1<y$. Prostokąt wyznaczony przez punkty: początek nawiasu, minus 0,5, 3,5, zamknięcie nawiasu, początek nawiasu, 0, 4, zamknięcie nawiasu, początek nawiasu , 2, 1, zamknięcie nawiasu, początek nawiasu 2,5, 1,5, zamknięcie nawiasu jest zamalowany kolorem ciemnofioletowym.

nierówność w jednej z postaci:

zbiór wszystkich punktów $\left(x, y\right)$, których współrzędne spełniają tą nierówność; półpłaszczyzna wyznaczona przez prostą $ax+by=c$

koniunkcja nierówności występujących w układzie

część wspólna zbiorów rozwiązań poszczególnych nierówności występujących w układzie