Przeczytaj

Podział trójkątów ze względu na kąty

TrójkątytrójkątTrójkąty możemy klasyfikować ze względu na ich kątykątkąty:

trójkąt ostrokątny ma wszystkie kąty ostre,
trójkąt prostokątny ma jeden kąt prosty,
trójkąt rozwartokątny ma jeden kąt rozwarty.

RpCELu5vE9DDX

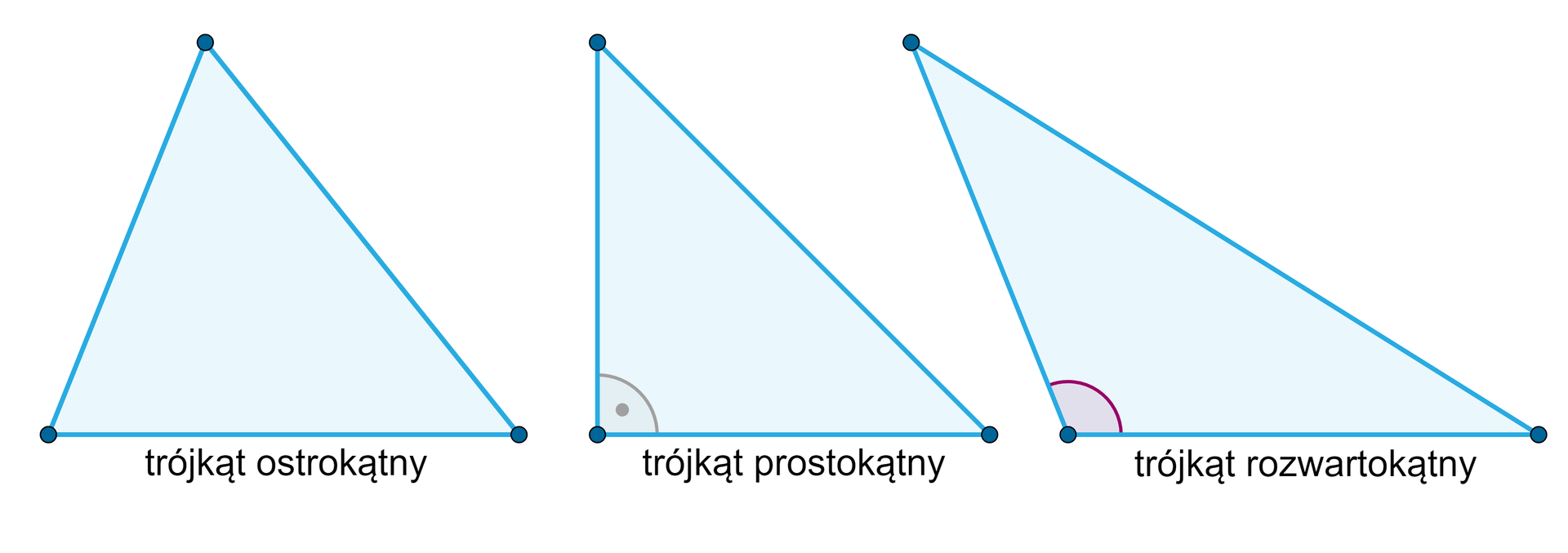
Ilustracja przedstawia trzy typy trójkątów. Pierwszy, trójkąt ostrokątny, jego wszystkie trzy kąty wewnętrzne są kątami ostrymi. Drugi, trójkąt prostokątny, jeden z jego kątów wewnętrznych jest kątem prostym. Trzeci, trójkąt rozwartokątny, jeden z jego kątów wewnętrznych jest kątem rozwartym.

oraz długość boków:

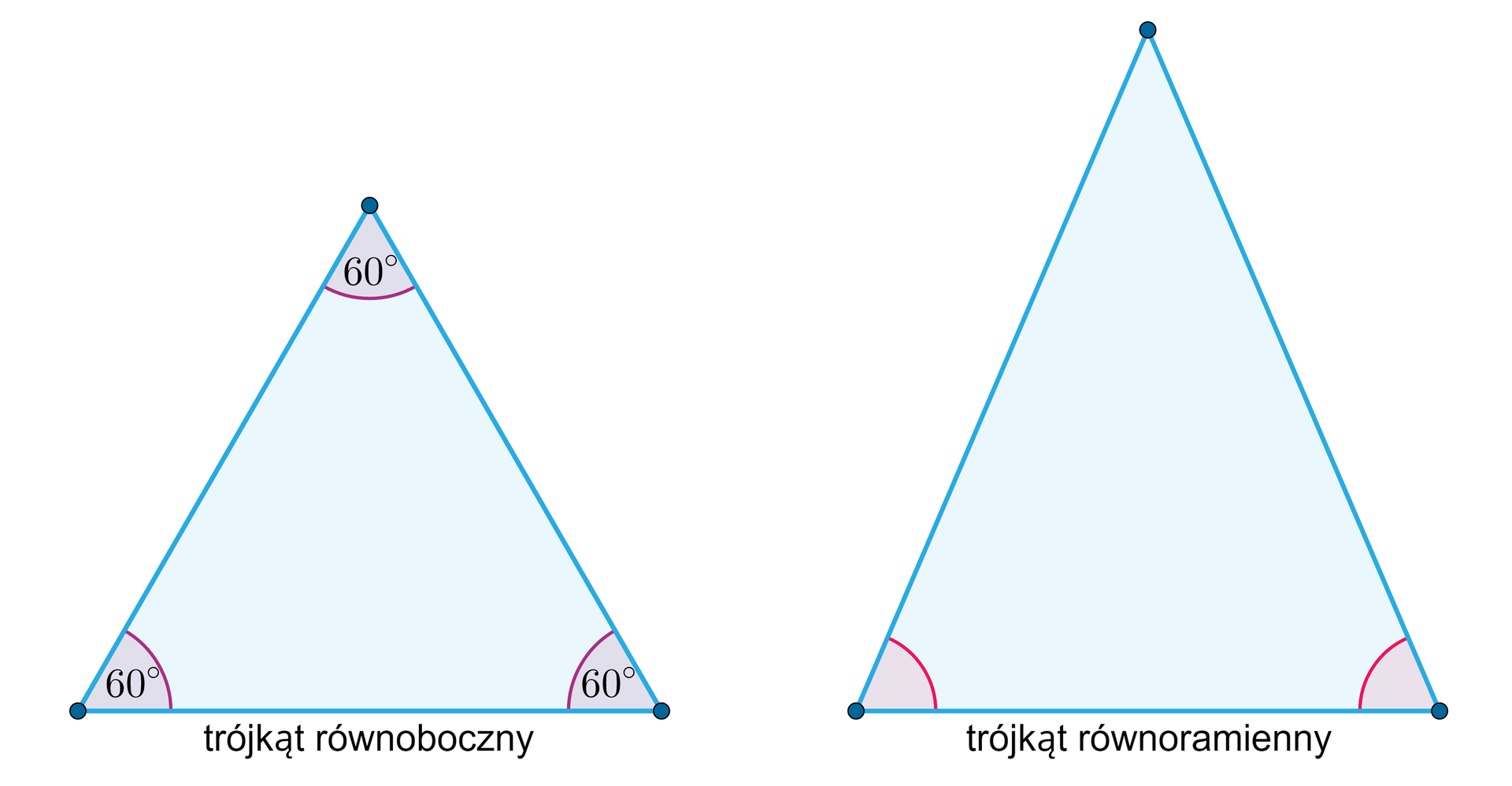
trójkąt równoboczny – trójkąt, którego wszystkie boki mają taką samą długość, szczególny przypadek trójkąta równoramiennego; jest przykładem wielokąta foremnego,
trójkąt równoramienny – trójkąt o (co najmniej) dwóch bokach równej długości; te dwa boki zwane są ramionami trójkąta, trzeci bok jego podstawą. Kąty przy podstawie są przystające, a ich miara jest mniejsza od miary kąta prostego.

R16Es6pH4hOmK

Ilustracja przedstawia dwa trójkąty. Pierwszy, trójkąt równoboczny, wewnątrz trójkąta podpisane zostały jego kąty wewnętrzne, wszystkie o mierze sześćdziesięciu stopni. Drugi, trójkąt równoramienny, wewnątrz trójkąta została zaznaczona para tych samych kątów. Oba kąty znajdują się pomiędzy ramieniem a podstawą trójkąta.

suma miar kątów wewnętrznych trójkąta

Twierdzenie: suma miar kątów wewnętrznych trójkąta

Suma miar kątów wewnętrznych trójkąta jest równa $180 °$ .

Dowód

Rozpatrzmy trójkąt $A B C$ . Narysujmy prostą przechodzącą przez wierzchołek $C$ i równoległą do odcinka $A B$ .

RSkyBeWbDTYu5

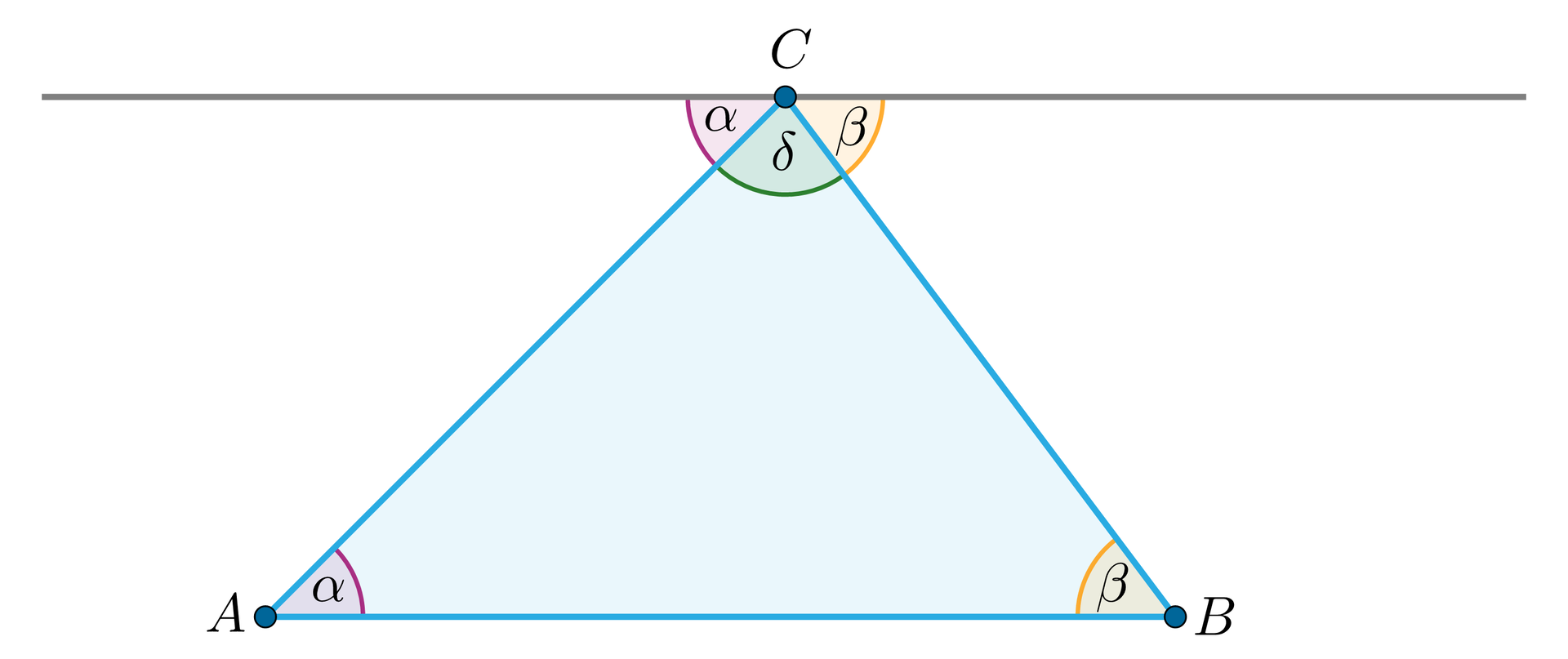
Ilustracja przedstawia trójkąt A B C. Przez punkt C przechodzi prosta k równoległa do odcinak A B. Na ilustracji zaznaczono kąty alfa, beta oraz delta. Kąt alfa znajduje się przy wierzchołku A oraz pomiędzy prostą k a odcinkiem A C. Kąt beta znajduje się przy wierzchołku B oraz pomiędzy prostą k a odcinkiem B C. Kąt delta znajduje się przy wierzchołku C.

Z faktu, że kąty naprzemianległe mają równe miary, otrzymujemy $α + β + γ = 180 °$ .

Przykład 1

Uzasadnimy, że suma miar kątów wewnętrznych $n$ -kąta wypukłego jest równa $(n - 2) \cdot 180 °$ .

Rozwiązanie

RZnvDlBo4Mk7f

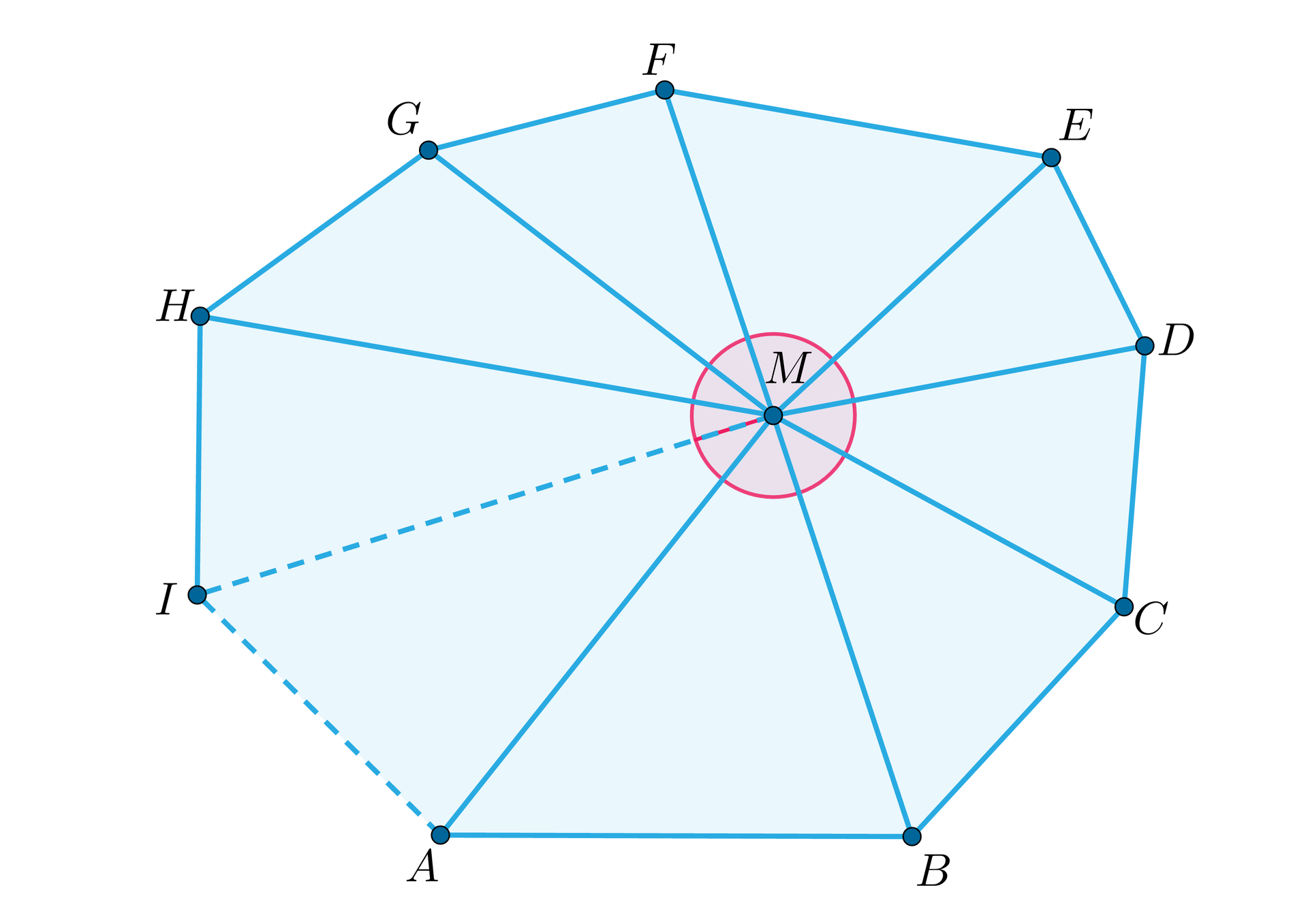
Ilustracja przedstawia dziewięciokąt nieforemny A B C D E F G H I. Wewnątrz figury zaznaczono punkt M i połączono go z każdym z wierzchołków figury. Punkt M jest jednocześnie środkiem małego czerwonego okręgu znajdującego się wewnątrz wielokąta.

Obierzmy wewnątrz wielokąta punkt $M$ . Łączymy ten punkt z kolejnymi wierzchołkami $n$ –kąta. Otrzymujemy $n$ trójkątów o wierzchołku $M$ . Jeśli od sumy miar kątów wewnętrznych we wszystkich trójkątach odejmiemy kątkątkąt pełny przy wierzchołku $M$ , to otrzymamy sumę miar kątów wewnętrznych $n$ –kąta wypukłego równą $n \cdot 180 ° - 360 ° = (n - 2) \cdot 180 °$ .

Uwaga!
Twierdzenie powyższe jest również prawdziwe w przypadku wielokątów wklęsłych. Jednak powyższy dowód, jak i wiele innych przytaczanych w podręcznikach do szkoły ponadpodstawowej, wymaga uzupełnienia.

Wniosek:
Miara kąta wewnętrznego w $n$ –kącie foremnym jest równa

\frac{(n - 2) \cdot 180 °}{n}

Teraz przekonamy się, że przytaczany wyżej dowód na sumę miar kątów wewnętrznych w wielokącie wypukłym w przypadku wielokąta wklęsłego rzeczywiście wymaga uzupełnienia.

Przykład 2

Podamy przykład wielokąta, dla którego nie istnieje taki punkt $M$ w jego wnętrzu, że odcinki łączące go z wierzchołkami znajdujące się wewnątrz tego wielokąta, dzielą ten wielokąt na trójkąty.

Rozwiązanie

Przypomnijmy, że przytoczony dowód na sumę miar kątów wewnętrznych w $n$ –kącie opierał się na zsumowaniu kątów wewnętrznych wszystkich trójkątów o wspólnym wierzchołku $M$ .

Rozważmy wielokąt:

Rp9k5UKUiBh5P

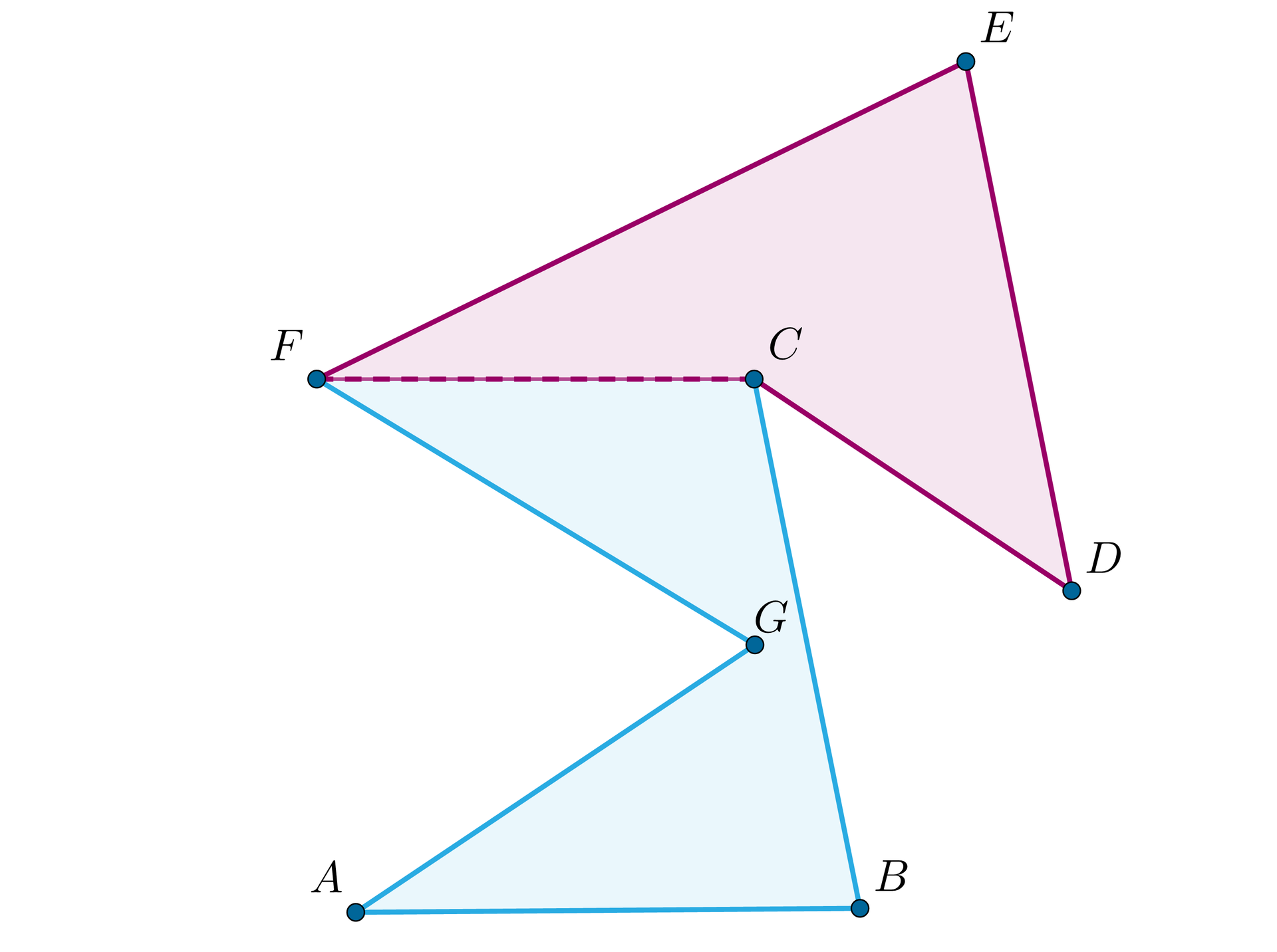
Ilustracja przedstawia wielokąt A B C D E F G. Wielokąt ten przypomina kształtem cztery zlepione ze sobą trójkąty. Trójkąty te jedna nie tworzą spójnej pojedynczej bryły, lecz bardziej przypominają poszarpaną strukturę.

Jeżeli wybierzemy punkt $M$ , który znajduje się pod odcinkiem $C F$ (lub na nim), to widzimy, że nie istnieje wewnątrz tego wielokąta trójkąt $M C D$ . Gdy wybierzemy punkt $M$ , który znajduje się nad odcinkiem $C F$ (lub na nim), wówczas wewnątrz tego wielokąta nie istnieje trójkąt $M A B$ .

Powyższy przykład pokazuje, że rozumowania z poprzedniego przykładu nie możemy zastosować do dowolnego wielokąta.

Przykład 3

Wyznaczymy sumę miar kątów zewnętrznychkąt zewnętrznykątów zewnętrznych w trójkącie, czworokącie, $n$ –kącie.

Rozwiązanie

Pokażemy, ze suma ta nie zależy od liczby wierzchołków wielokąta wypukłego. Suma kąta wewnętrznego i jednego przyległego do niego kąta zewnętrznego jest równa $180^{\circ}$ . Pamiętajmy, że do kąta wewnętrznego przylegają dwa kąty zewnętrzne. Wnioskujemy stąd, że suma kątów wewnętrznych i połowy wszystkich kątów zewnętrznych w $n$ –kącie jest równa $n \cdot 180 °$ . Ponadto znamy już wzór na sumę kątów wewnętrznych: $(n - 2) \cdot 180 °$ . Zatem suma wszystkich kątów zewnętrznych jest równa $2 \cdot [n \cdot 180 ° - (n - 2) \cdot 180 °] = 2 \cdot 360 ° = 720 °$ .

Inny, bardzo ładny dowód powyższego faktu, opiera się na pojęciu kąta skierowanego, czyli takiego, w którym rozróżniamy kolejność ramion kąta. Można sobie wyobrazić, że „spacerując” po obwodzie wielokąta w każdym wierzchołku skręcamy o kąt, którego miara jest równa kątowi zewnętrznemu. Oczywiście przechodząc cały obwód i wracając do punktu wyjścia obrócimy się o kąt $360 °$ . Powtarzając spacer w przeciwnym kierunku również obrócimy się o kąt $360 °$ . Zatem suma wszystkich kątów zewnętrznych w $n$ –kącie wypukłym wynosi $720 °$ .

Przykłady zadań związanych z wyznaczaniem miar kątów w trójkącie

Przykład 4

Trójkąt równoramienny $A B C$ , w którym $|A C| = |B C|$ rozcięto odcinkiem $A D$ na dwa trójkąty równoramienne $B D A$ i $C A D$ tak, że $|A B| = |A D| = |C D|$ . Wyznaczymy miary kątów trójkąta $A B C$ .

Rozwiązanie

R1127dPK4Izi1

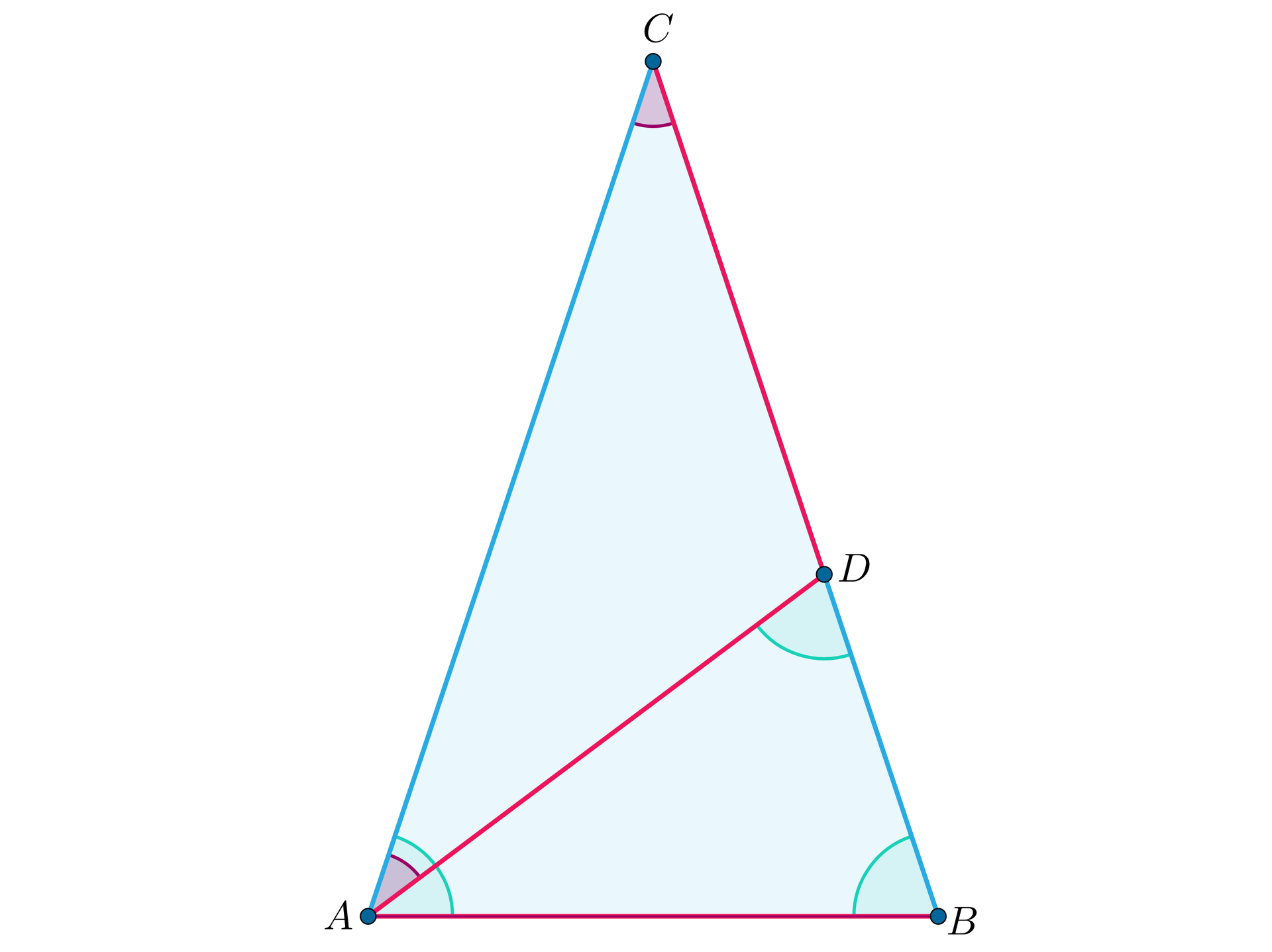
Ilustracja przedstawia trójkąt równoramienny A B C. Z wierzchołka A na przeciwległy bok poprowadzono prostą dzielącą odcinek C B w punkcie D w taki sposób, że powstały dwa trójkąty równoramienne. Pierwszy, trójkąt A D C, gdzie ramionami trójkąta są odcinki A D i C D. Oraz drugi trójkąt A B D, gdzie ramionami tego trójkąta są odcinki A D i A B.

Oznaczmy przez $α$ kąt przy wierzchołku $C$ . Z założeń wiemy, że $|∢ C A D| = |∢ A C D| = α$ , więc $|∢ A D C| = 180 ° - 2 α$ . Kąt $A D B$ jest przyległy do kąta $A D C$ , więc jego miara jest równa $2 α$ . Ponadto, z warunków zadania wiemy, że $|∢ A D B| = |∢ A B D| = |∢ B A C| = 2 α$ . Teraz wystarczy, że zsumujemy kąty wewnętrzne w trójkącie $A B C$ lub $A B D$ i otrzymujemy $α + 2 α + 2 α = 180^{\circ},$ czyli: $5 α = 180^{\circ}$ . Ostatecznie otrzymujemy $72 °$ , $72 °$ , $36 °$ .

Przykład 5

W trójkącie $A B C$ środkowa i wysokość opuszczone z wierzchołka $C$ dzielą ten kąt na trzy równe części. Wyznaczymy miary kątów tego trójkąta.

Rozwiązanie

Oznaczmy spodek wysokości przez $D$ , a punkt przecięcia środkowej z odcinkiem $A B$ przez $E$ .

Z punktu $E$ prowadzimy prostopadłą do boku $A C$ . Ich przecięcie oznaczamy przez $F$ .

R1WRzdiQHHFTZ

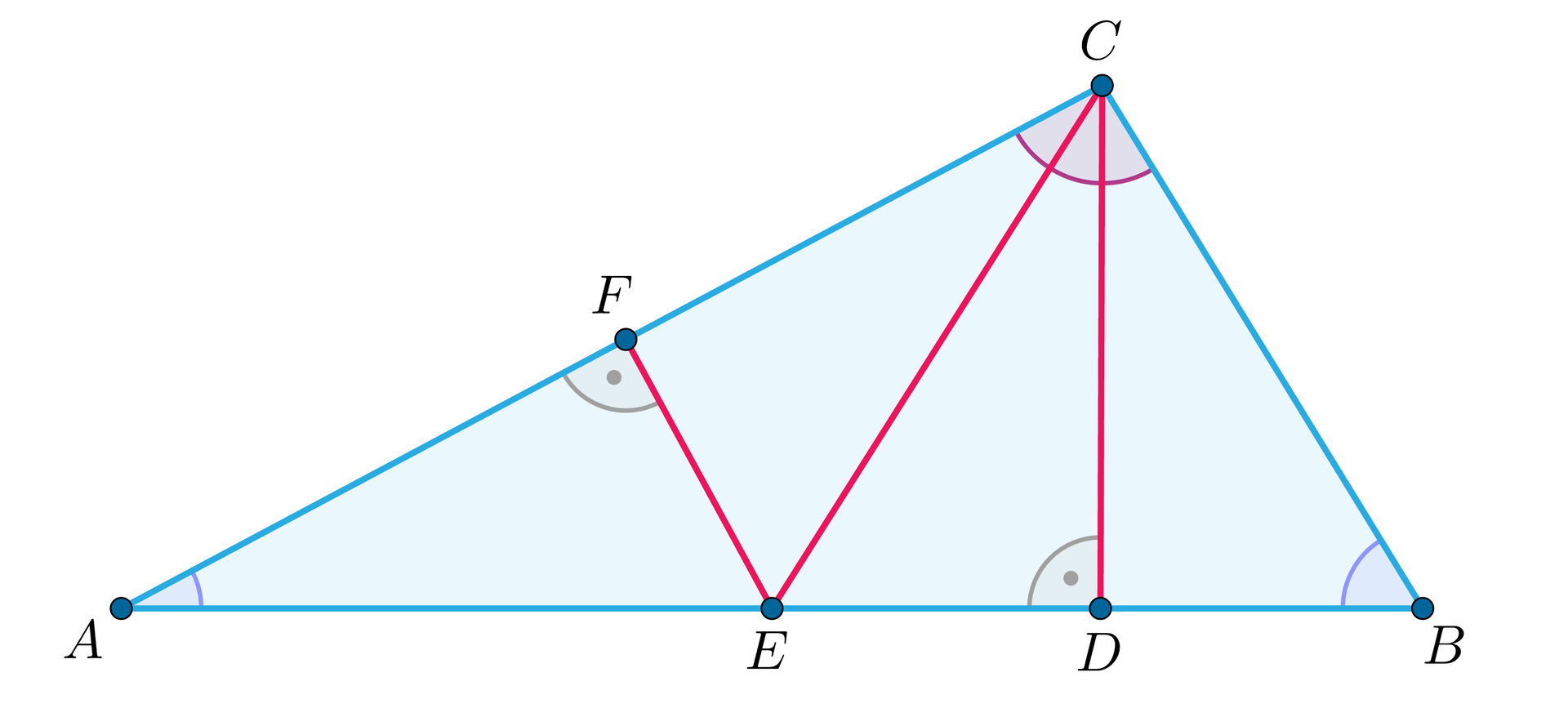
Ilustracja przedstawia trójkąt A B C . Z punktu C poprowadzono środkową boku B C w punkcie E, a także upuszczono wysokość figury w punkcie D. Powstały dwa trójkąty równoramienne, trójkąt E B C oraz trójkąt A E C. W trójkącie A E C z wierzchołka E upuszczono wysokość na bok A C w punkcie F.

Trójkąty $B D C$ , $E D C$ są prostokątne, ponadto mają wspólny odpowiadający bok i równe kąty ( $∢ E C D = ∢ D C B$ ), więc są przystające (kbk). Podobnie trójkąty $E D C$ i $E F C$ ( $∢ E C D = ∢ F C E$ ). Zatem $|E F| = |E D| = |D B| = \frac{1}{2} |E B| = \frac{1}{2} |A E|$ .

Wynika z tego, że trójkąt $A E F$ jest połową trójkąta równobocznego o boku $A E$ . Zatem
$|∢ E A F| = |∢ B A C| = 30 °$

$|∢ B E F| = 120 °$ $|∢ A B C| = |∢ D E C| = |∢ C E F| = \frac{1}{2} \cdot 120 ° = 60 °$
$|∢ A C B| = 90 °$ .

Ciekawostka

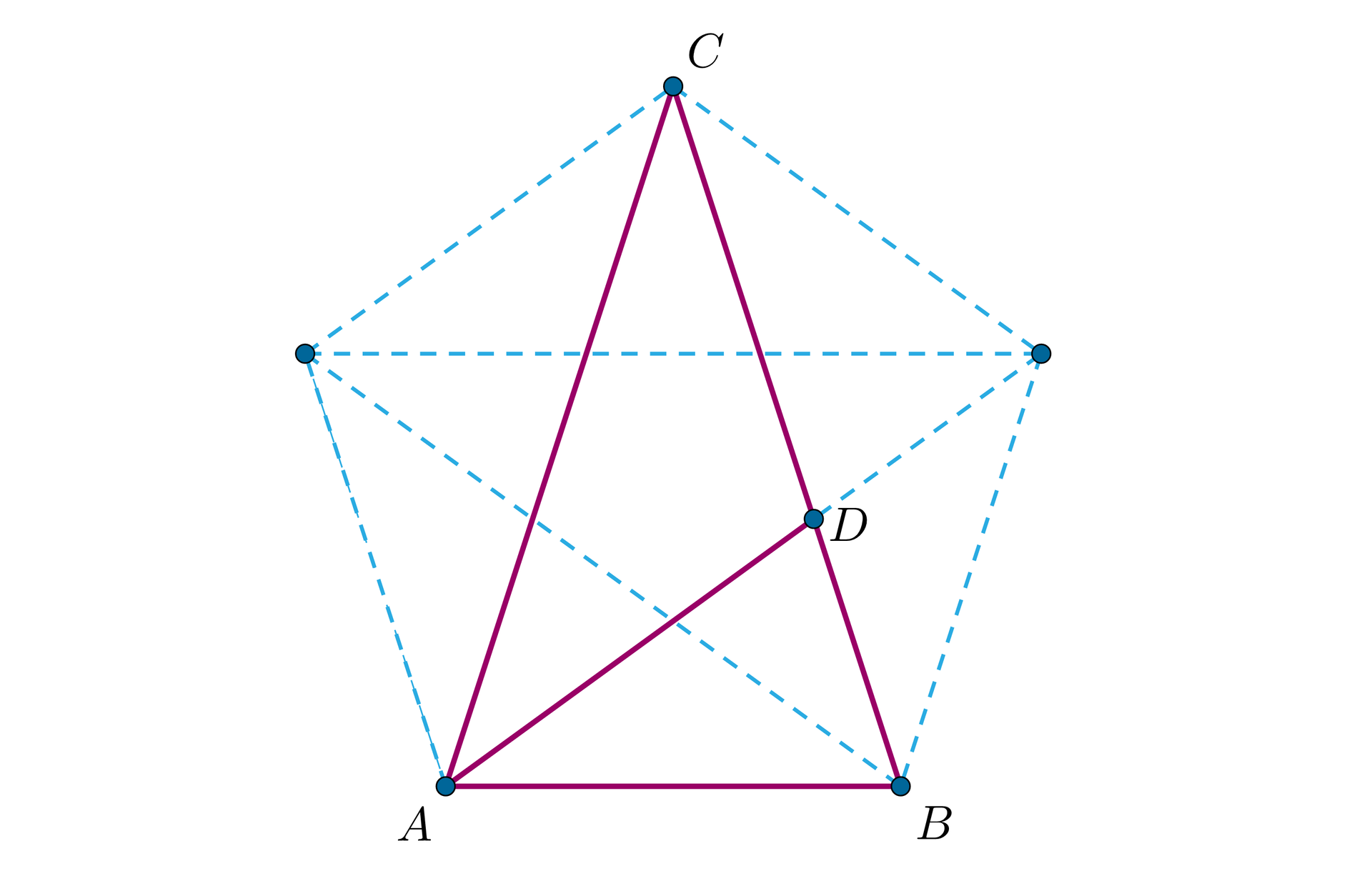
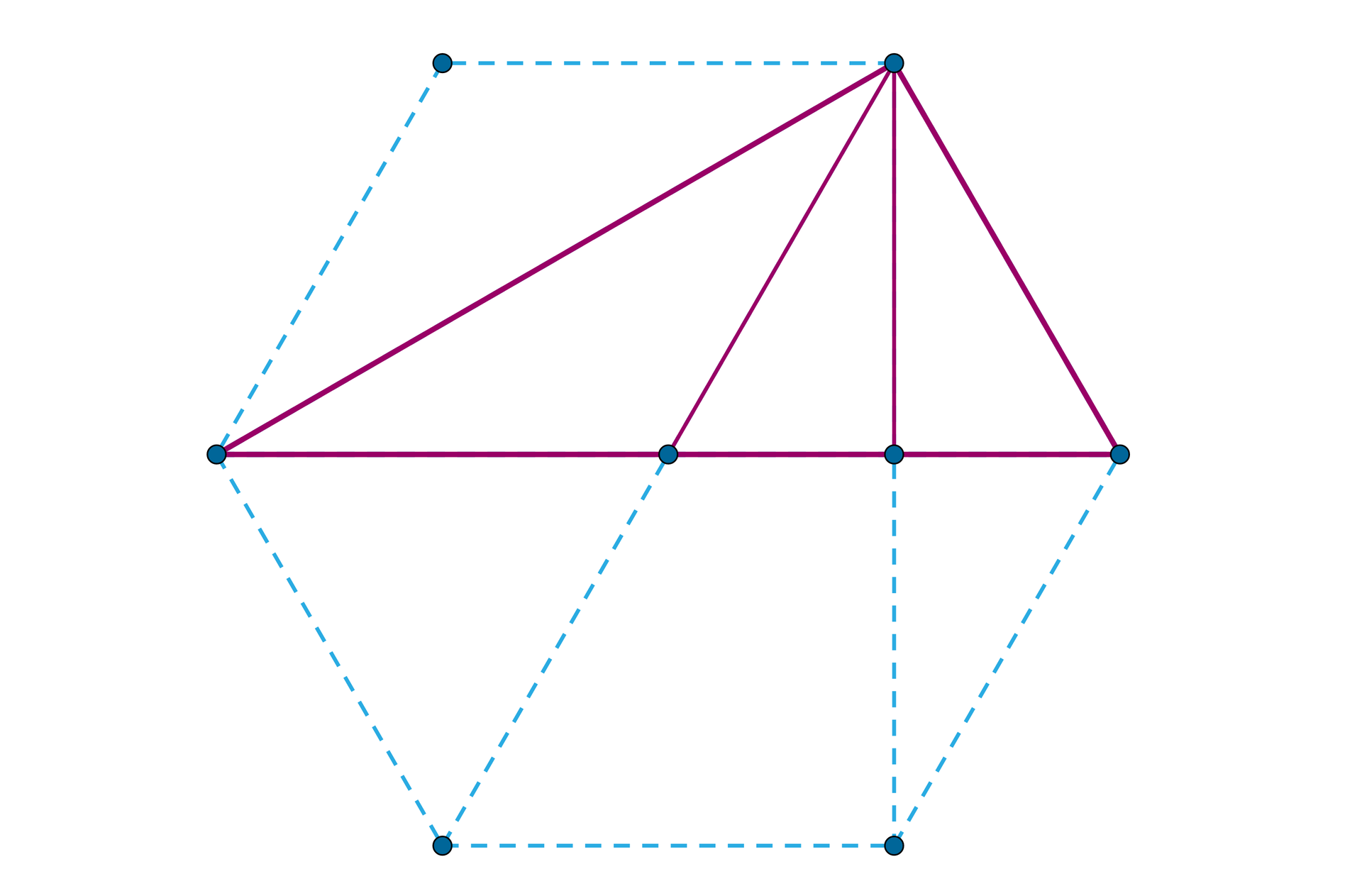
Rysunki do powyższych dwóch przykładów to wybrane wierzchołki, boki lub przekątne pewnych wielokątów foremnych. Powyższa obserwacja może nam znacząco ułatwić zarówno konstrukcję założeń zadania, jak i odkrywanie zależności niezbędnych do jego rozwiązania.

R1ZMMbHzXgiOJ

Ilustracja przedstawia trójkąt równoramienny A B C zbudowany na bazie pięciokąta foremnego z zaznaczonymi wszystkimi przekątnymi. W trójkącie A B C z wierzchołka A na przeciwległy bok poprowadzono prostą dzielącą odcinek C B w punkcie D w taki sposób, że powstały dwa trójkąty równoramienne. Pierwszy, trójkąt A D C, gdzie ramionami trójkąta są odcinki A D i C D. Oraz drugi trójkąt A B D, gdzie ramionami tego trójkąta są odcinki A D i A B.

R16IkceLB1gLl

Słownik

trójkąt

figura wyznaczona przez trzy punkty nieleżące na jednej prostej, każdy z tych punktów jest wierzchołkiem trójkąta a odcinki łączące wierzchołki nazywamy bokami

kąt

obszar powstały z rozcięcia płaszczyzny przez sumę dwóch różnych półprostych o wspólnym początku, wraz z tymi półprostymi; półproste nazywane są ramionami kąta, wspólny początek półprostych nazywany jest wierzchołkiem kąta

kąt zewnętrzny

kąt przyległy do danego kąta wewnętrznego wielokąta; jeżeli dany kąt wewnętrzny w pewnym wierzchołku wielokąta nie jest wypukły, to nie istnieje kąt zewnętrzny do niego w tym wierzchołku

Wprowadzenie

Prezentacja multimedialna

Podział trójkątów ze względu na kąty

Przykłady zadań związanych z wyznaczaniem miar kątów w trójkącie

Słownik