Przeczytaj
Przypomnijmy, jak wygląda model oraz w jaki sposób obliczamy pole powierzchni całkowitej i objętość graniastosłupa prawidłowego trójkątnegograniastosłupa prawidłowego trójkątnego.
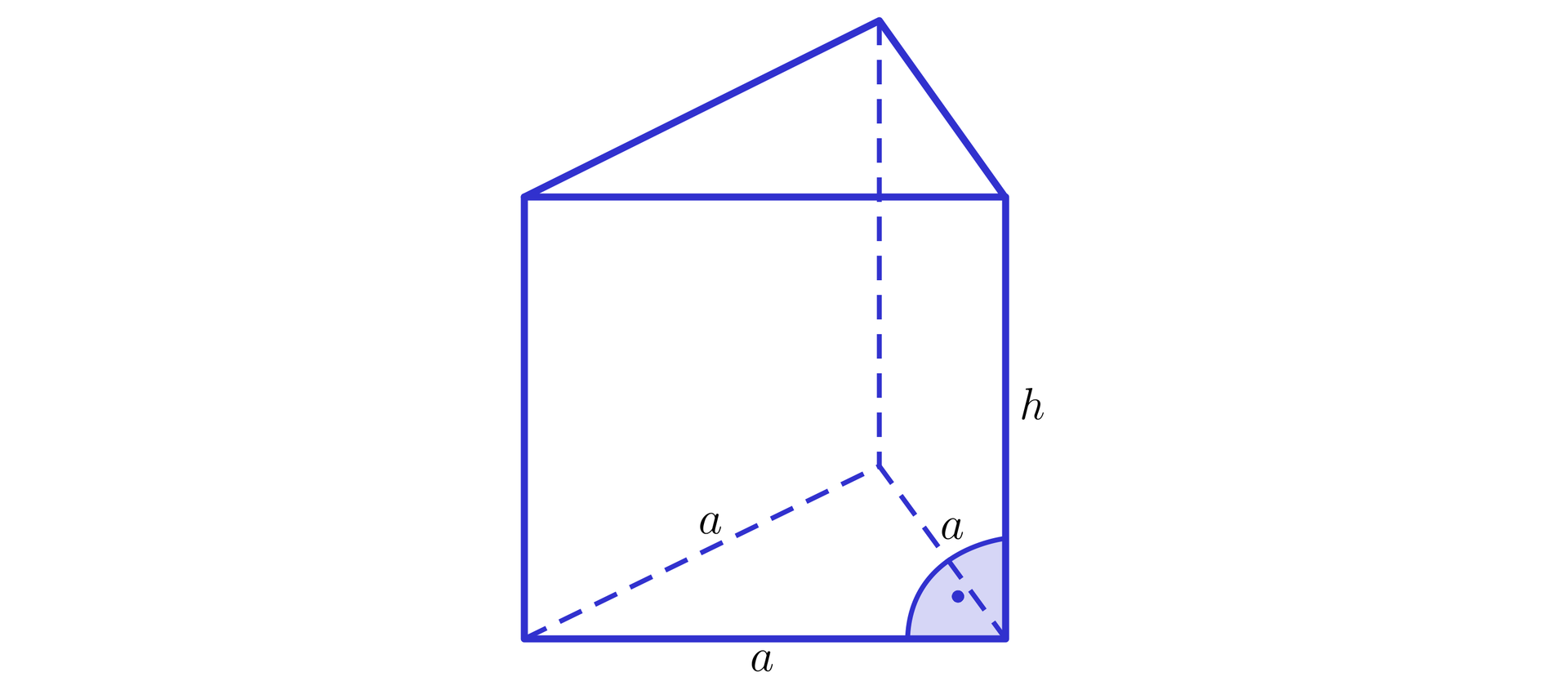
Pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnego o wymiarach, jak na rysunku wyraża się wzorem:
Objętość graniastosłupa prawidłowego trójkątnego o wymiarach, jak na rysunku wyraża się wzorem:
W graniastosłupie prawidłowym trójkątnym możemy znajdować miary kątów pomiędzy różnymi płaszczyznami, co sprowadza się do narysowania odpowiedniego kąta dwuściennego, a następnie wyznaczenia jego miary.
Miarą liniową kąta dwuściennego jest miara kąta płaskiego, który leży w przekroju kąta dwuściennego i płaszczyzny prostopadłej do krawędzi kąta dwuściennego.
W graniastosłupie prawidłowym trójkątnym możemy wyróżnić wiele kątów pomiędzy różnymi płaszczyznami, np.:
Kąt nachylenia płaszczyzny przekroju graniastosłupa prawidłowego trójkątnego przechodzącej przez krawędź podstawy i przeciwległy wierzchołek drugiej podstawy graniastosłupa do płaszczyzny podstawy graniastosłupa.
RKrTEJVCnNHYP 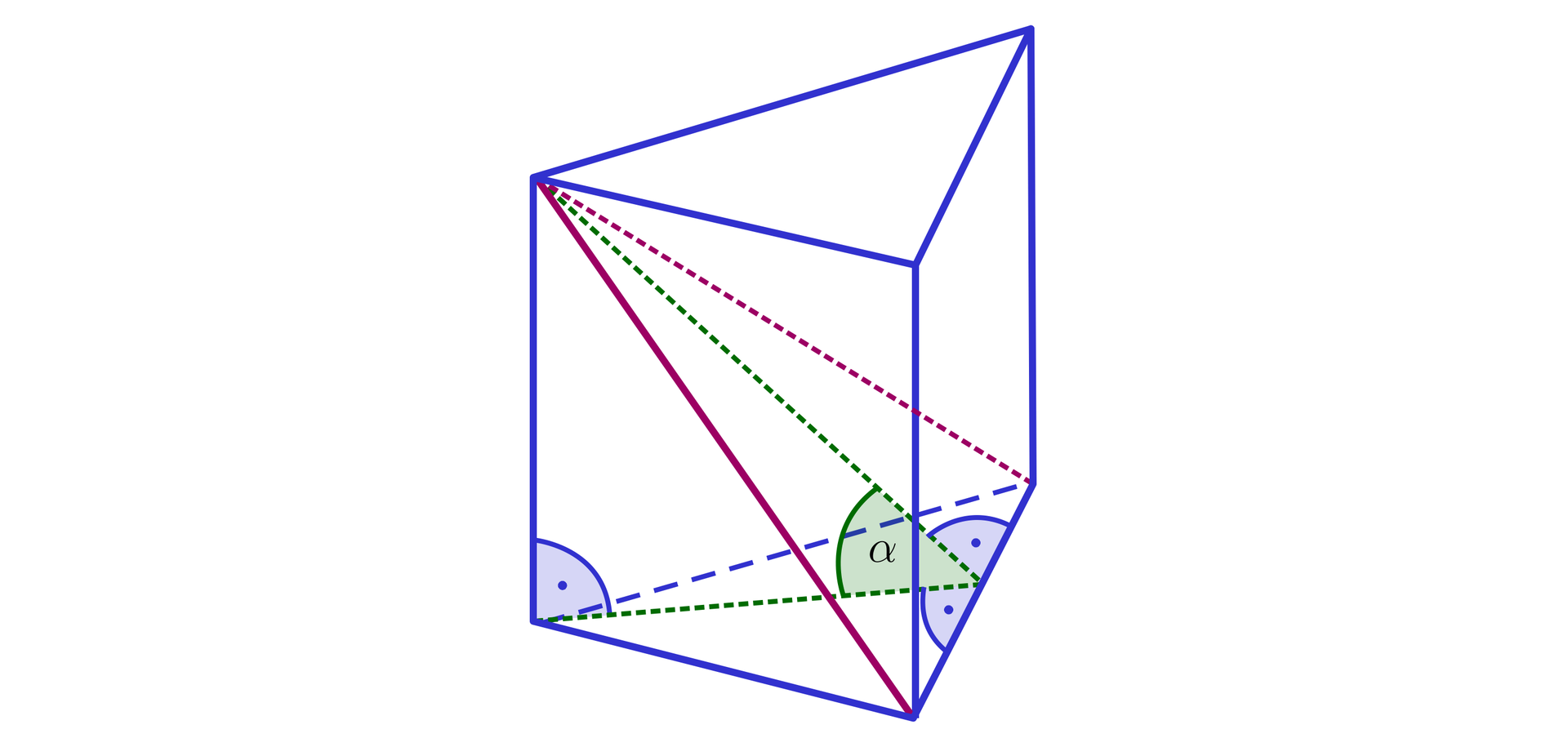
Kąt nachylenia płaszczyzny przekroju graniastosłupa prawidłowego trójkątnego przechodzącej przez krawędź podstawy i punkt należący do przeciwległej krawędzi bocznej do płaszczyzny podstawy graniastosłupa.
R10PlukjwL6FU 
Kąt nachylenia płaszczyzny przekroju graniastosłupa prawidłowego trójkątnego przechodzącej przez wysokość dolnej podstawy i wierzchołek górnej podstawy do płaszczyzny podstawy graniastosłupa.
R1b9szf5gW7AJ 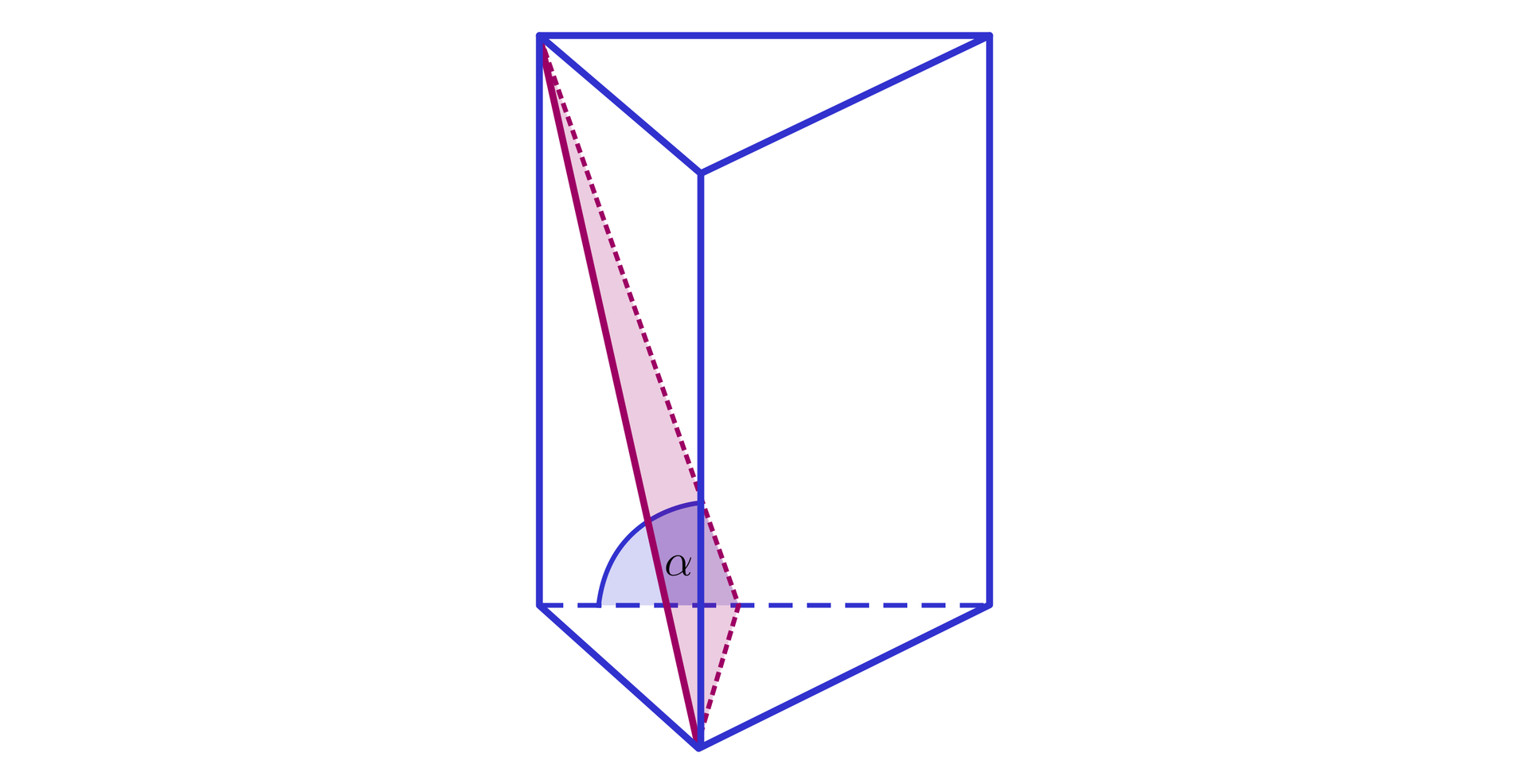
Do wyznaczania miar kątów między płaszczyznami w graniastosłupie prawidłowym trójkątnym będziemy używali wartości funkcji trygonometrycznychfunkcji trygonometrycznych.
Obliczymy miarę kąta nachylenia płaszczyzny przekroju graniastosłupa prawidłowego trójkątnego do płaszczyzny jego podstawy jeżeli wiadomo, że płaszczyzna przechodzi przez krawędź dolnej podstawy i środek przeciwległej krawędzi bocznej tak, jak na poniższym rysunku.
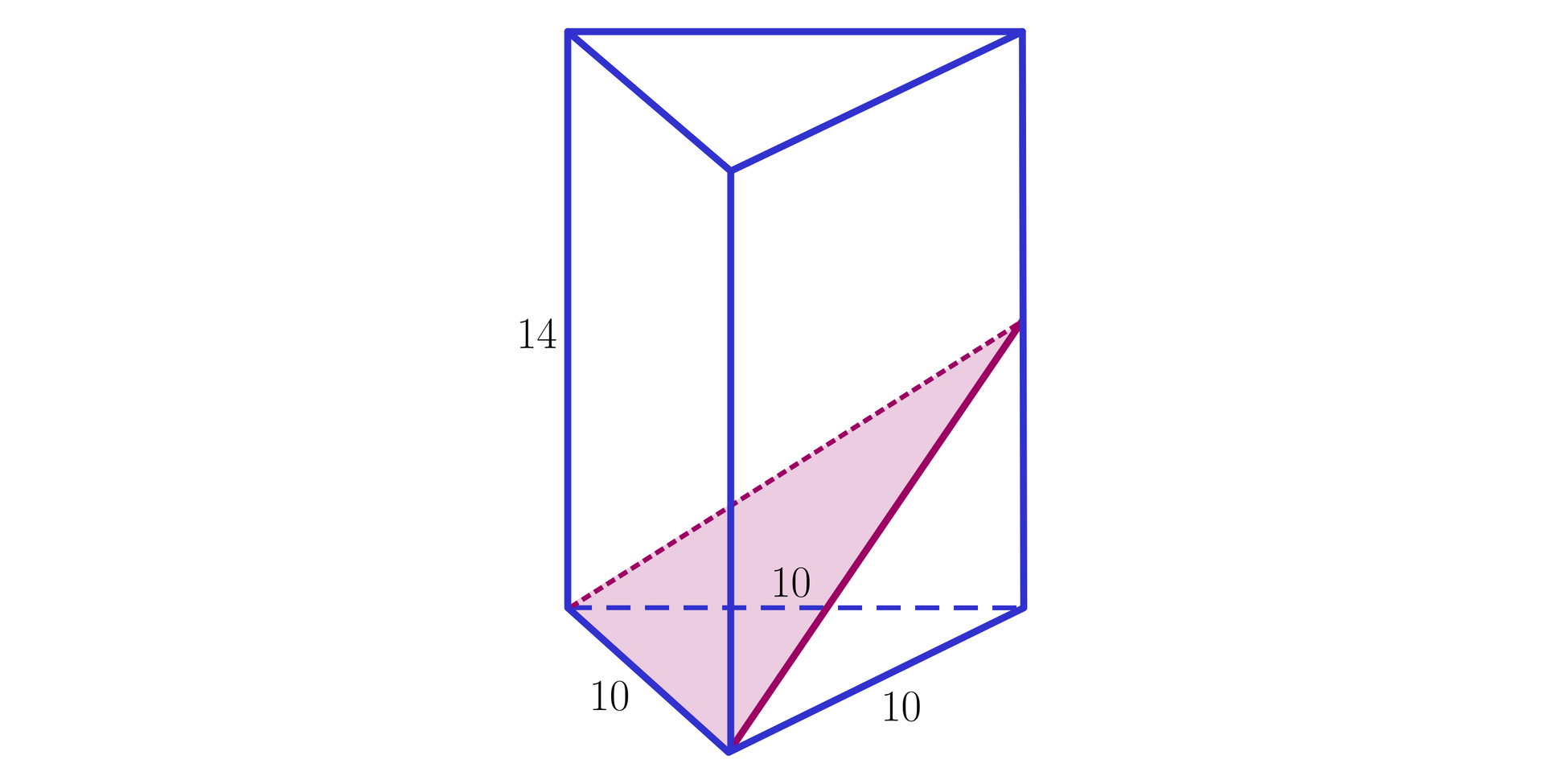
Rozwiązanie:
Zaznaczmy odpowiedni kąt i wprowadźmy oznaczenia, jak na poniższym rysunku.

Wobec tego do wyznaczenia miary kąta rozpatrujemy trójkąt prostokątny, jak na poniższym rysunku.
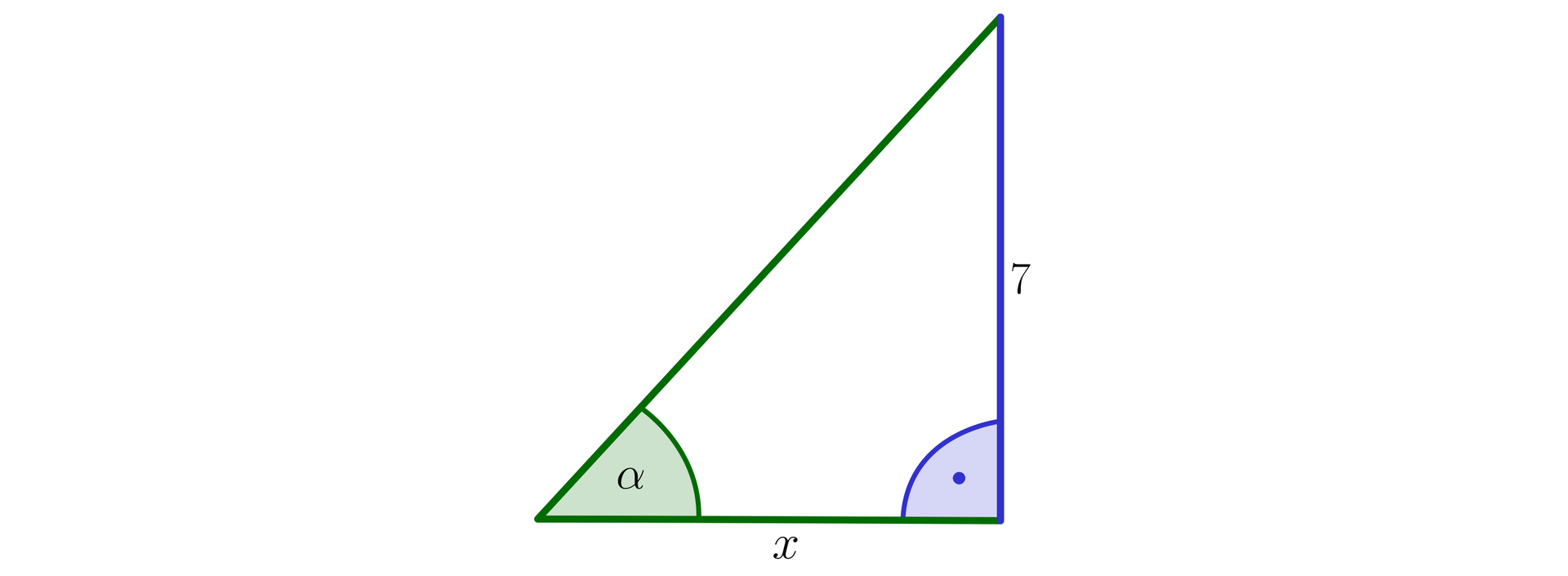
Zauważmy, że .
Zatem korzystając z funkcji trygonometrycznej tangens otrzymujemy, że:
Z tablic wartości funkcji trygonometrycznych odczytujemy, że .
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są jednakowej długości. Obliczymy miarę kąta nachylenia zaznaczonej płaszczyzny do płaszczyzny podstawy tego graniastosłupa.

Rozwiązanie:
Wprowadźmy oznaczenia na rysunku i zaznaczmy odpowiedni kąt.
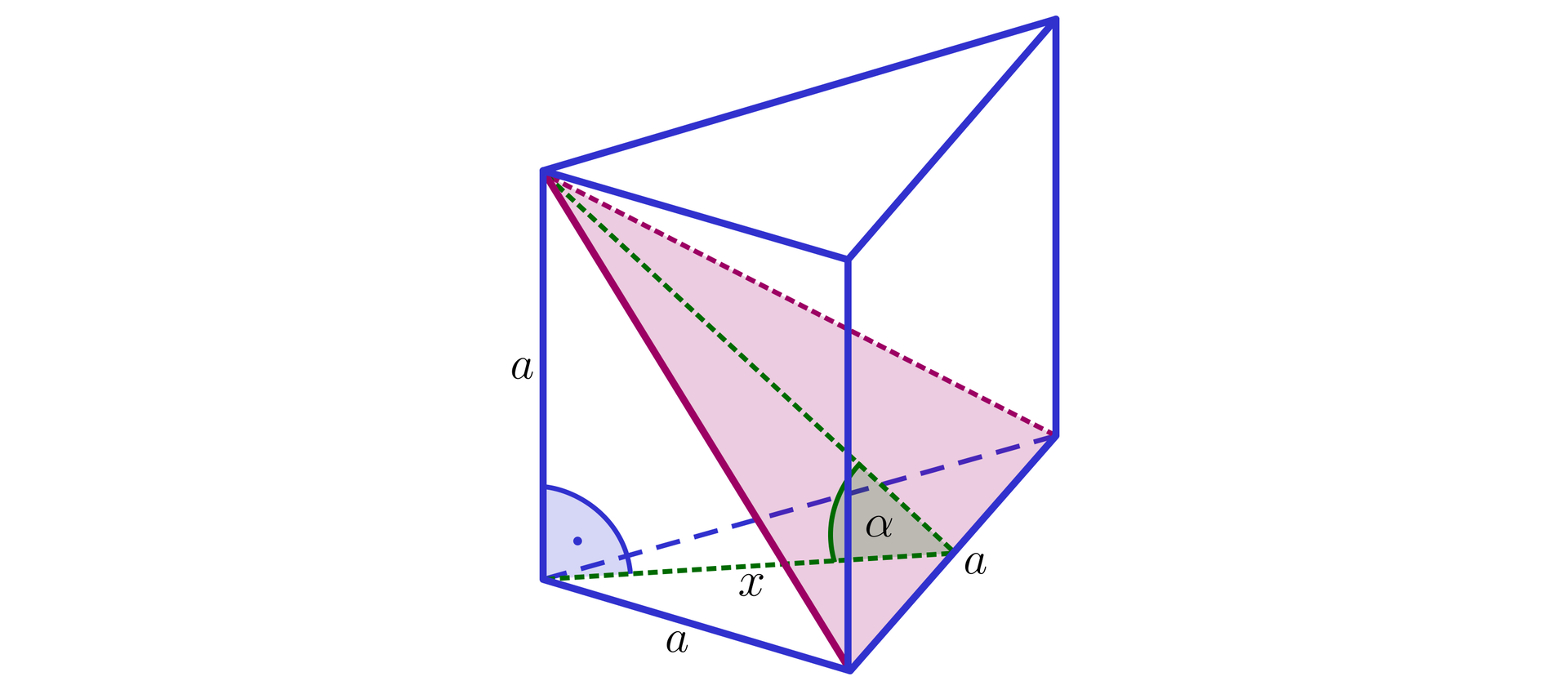
Do wyznaczenia miary kąta rozpatrujemy trójkąt prostokątny, jak na poniższym rysunku.
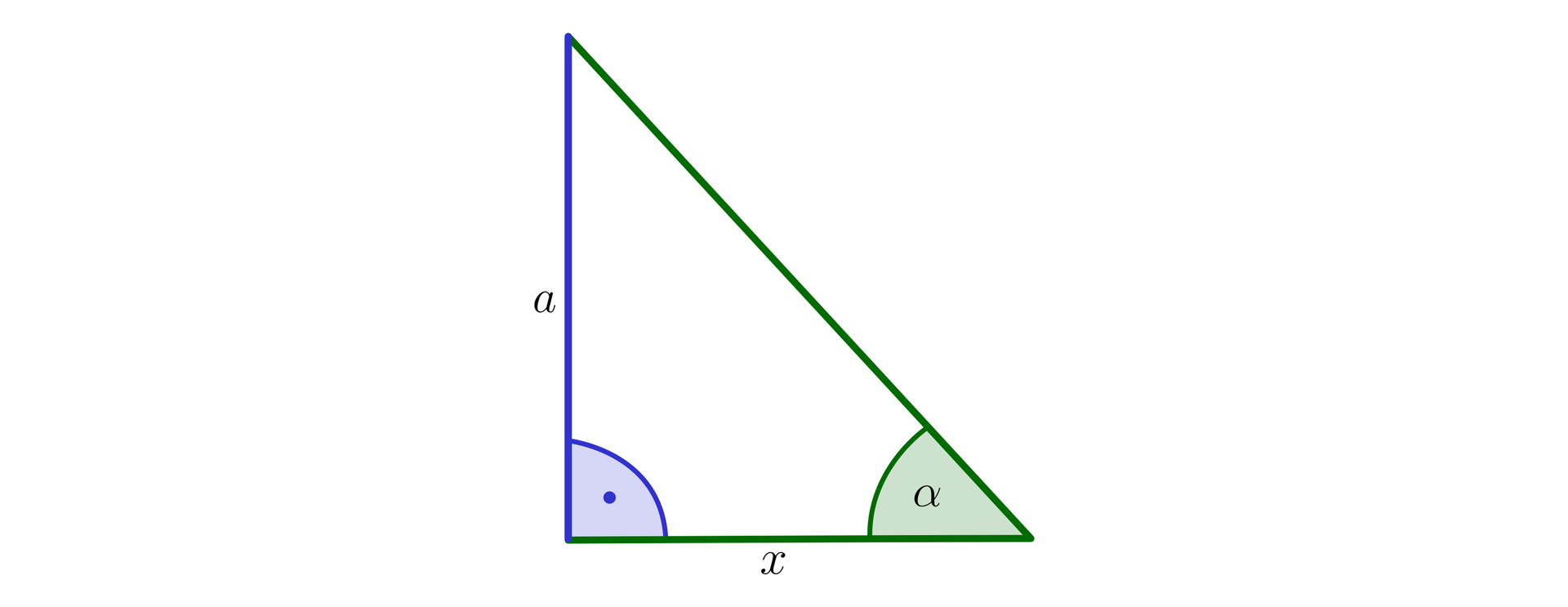
Zauważmy, że .
Korzystając z definicji funkcji trygonometrycznej tangens otrzymujemy, że:
Odczytujemy z tablic wartości funkcji trygonometrycznych, że .
W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy równej poprowadzono płaszczyznę przechodzącą przez wysokość podstawy oraz wierzchołek górnej podstawy. Wiedząc, że płaszczyzna ta tworzy z płaszczyzną podstawy kąt o mierze obliczymy pole powierzchni oraz objętość tego graniastosłupa.
Rozwiązanie:
Narysujmy graniastosłup prawidłowy trójkątny, płaszczyznę przekroju i wprowadźmy oznaczenia, jak na poniższym rysunku.
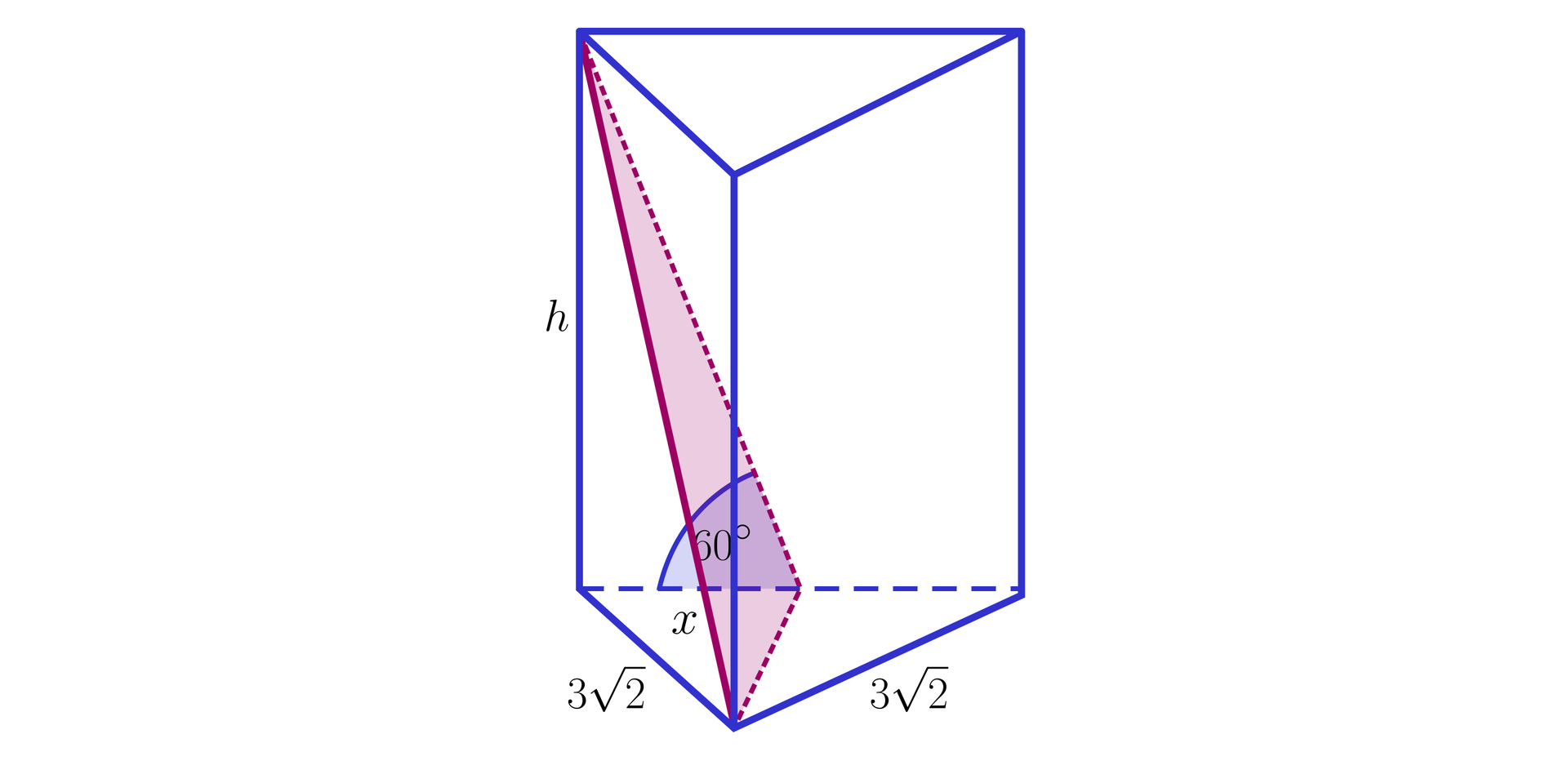
Wobec tego do wyznaczenia wartości korzystamy z trójkąta prostokątnego, jak na poniższym rysunku.
Zauważmy, że oraz
Obliczamy pole powierzchni oraz objętość omawianego graniastosłupa:
Graniastosłup prawidłowy trójkątny przecięto płaszczyzną, przechodzącą przez środek ciężkości górnej podstawy i krawędź dolnej podstawy, nachyloną pod kątem do dolnej podstawy. Obliczymy pole powierzchni tego graniastosłupa, jeżeli krawędź podstawy ma długość .
Rozwiązanie:
Narysujmy graniastosłup prawidłowy trójkątny, zaznaczmy odpowiedni kąt i wprowadźmy oznaczenia, jak na poniższym rysunku.

Wiadomo, że środek ciężkości dzieli wysokość podstawy graniastosłupa będącej trójkątem równobocznym w stosunku .
Zatem
Ponieważ , to .
Obliczamy pole powierzchni omawianego graniastosłupa:
W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy długości przekątne ścian bocznych, wychodzące z jednego wierzchołka tworzą kąt taki, że . Obliczymy pole powierzchni oraz objętość graniastosłupa.
Rozwiązanie:
Narysujmy graniastosłup prawidłowy trójkątny, zaznaczmy odpowiedni kąt i wprowadźmy oznaczenia, jak na poniższym rysunku.
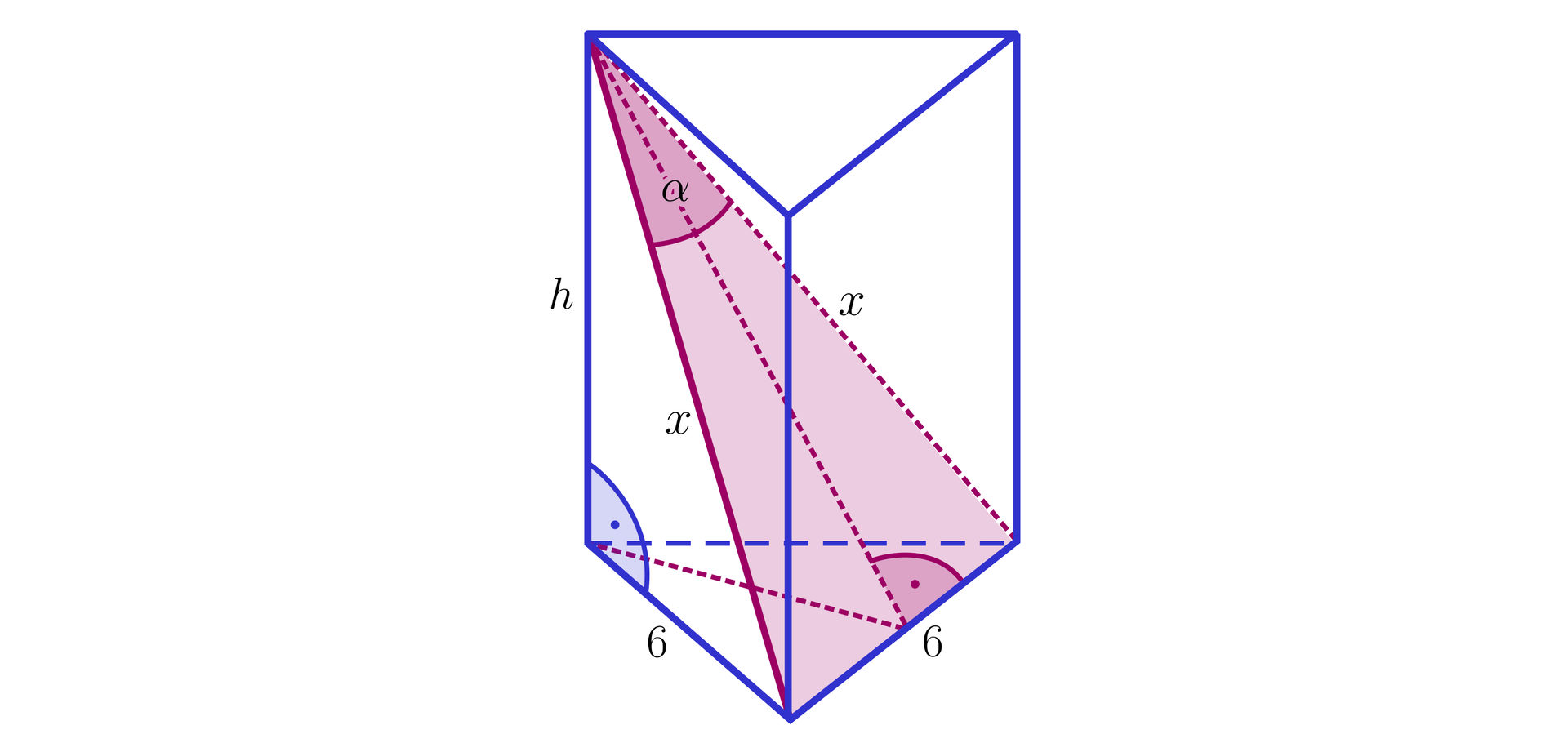
Korzystając z twierdzenia cosinusów, do wyznaczenia wartości rozwiązujemy równanie:
Wobec tego do wyznaczenia wartości rozpatrujemy trójkąt prostokątny, jak na poniższym rysunku.
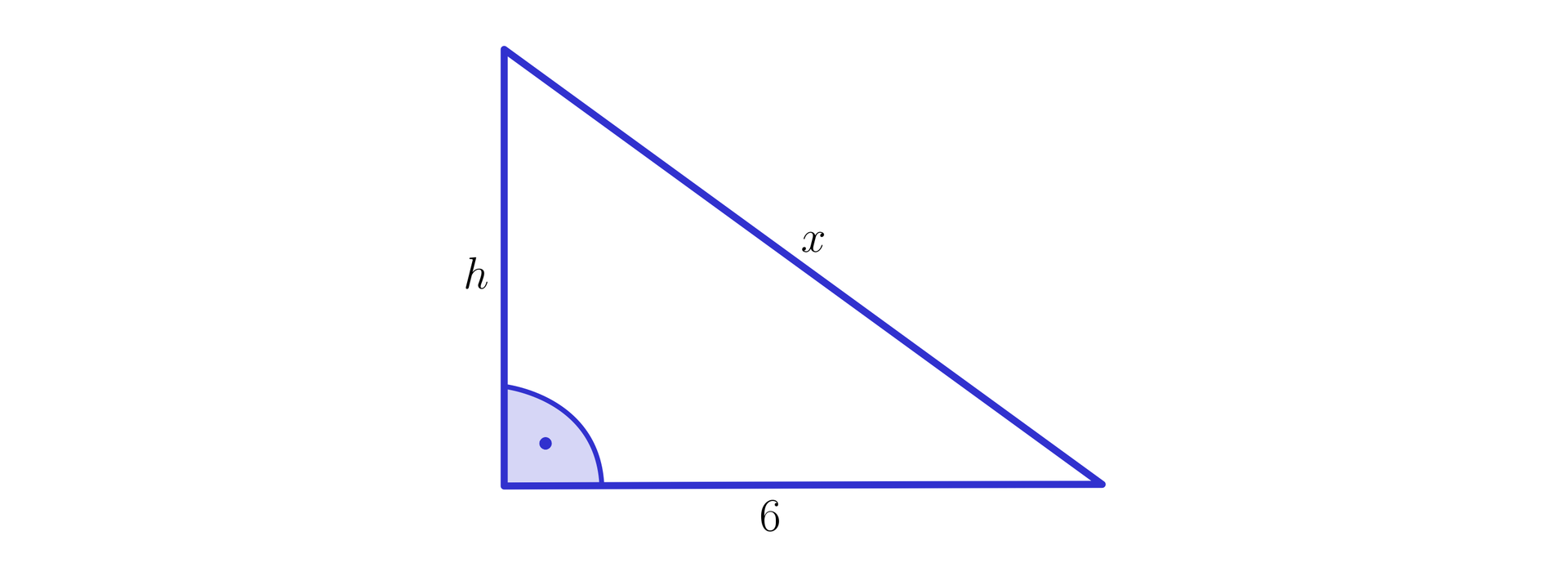
Korzystając z twierdzenia Pitagorasa mamy, że:
Obliczamy pole powierzchni oraz objętość graniastosłupa prawidłowego trójkątnego:
Słownik
graniastosłup prosty, którego podstawą jest trójkąt równoboczny
funkcje matematyczne, wyrażające stosunki między długościami boków trójkąta prostokątnego względem miar jego kątów wewnętrznych