Przeczytaj

Dowód, to ścisłe uzasadnienie danego stwierdzenia, przebiegające zgodnie z ustalonymi regułami. Zdanie opisujące własności danych obiektów matematycznych może zostać uznane za twierdzenie, dopiero po przedstawieniu poprawnego dowodu.

W matematyce istnieje wiele rodzajów dowodów. My będziemy posługiwali się dowodem wprost. Prawdziwość tezy będziemy dowodzić bezpośrednio przez dedukcję, korzystając z przyjętych założeń. Kolejne formuły w dowodzie będą wynikały logicznie z poprzednich, albo będą zdaniami, które przyjmuje się za oczywiste (wynikające z przyjętych aksjomatów).

Na początek przypomnienie najważniejszych wzorów dotyczących ciągu geometrycznego, z których będziemy korzystać.

Będziemy przy tym zakładać, że dany ciąg, np. ciąg $(a_{n})$ , jest określony dla $n \geq 1$ i $n \in ℕ$ .

Ciąg geometryczny

Definicja: Ciąg geometryczny

Ciągiem geometrycznym nazywamy ciąg liczbowy co najmniej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje przez pomnożenie wyrazu poprzedniego przez liczbę $q$ , zwaną ilorazem ciągu.

Ciąg geometryczny $(a_{n})$
Wyraz ogólny ciągu	Zależność między trzema kolejnymi wyrazami ciągu	Suma $n$ początkowych wyrazów ciągu
$a_{n} = a_{1} \cdot q^{n - 1}$	$a_{n}^{2} = a_{n - 1} \cdot a_{n + 1}$	$S_{n} = a_{1} \cdot \frac{1 - q^{n}}{1 - q}$

W pierwszym z dowodów wykorzystamy wzór na wyraz ogólny ciągu geometrycznego, ale również odwołamy się do własności działań na potęgach.

Przykład 1

Iloraz ciągu geometrycznego $(a_{n})$ jest równy $\frac{1 + \sqrt{5}}{2}$ . Pierwszy wyraz ciągu jest różny od $0$ . Wykażemy, że każdy wyraz tego ciągu, począwszy od drugiego wyrazu, jest równy różnicy dwóch sąsiadujących z nim wyrazów.

Założenie:

$(a_{n})$ – ciąg geometryczny

$a_{1} \neq 0$ , $q = \frac{1 + \sqrt{5}}{2}$

Teza:

$a_{n} = a_{n + 1} - a_{n - 1}$

Dowód:

Korzystamy ze wzoru ogólnego ciągu geometrycznego.

$a_{n + 1} = a_{1} \cdot q^{n} = a_{1} \cdot {(\frac{1 + \sqrt{5}}{2})}^{n}$

$a_{n - 1} = a_{1} \cdot q^{n - 2} = a_{1} \cdot {(\frac{1 + \sqrt{5}}{2})}^{n - 2}$

Zapisujemy różnicę $a_{n + 1} - a_{n - 1}$ za pomocą uzyskanych wyrażeń.

$a_{n + 1} - a_{n - 1} = a_{1} \cdot {(\frac{1 + \sqrt{5}}{2})}^{n} - a_{1} \cdot {(\frac{1 + \sqrt{5}}{2})}^{n - 2}$

Z prawej strony zapisanej równości wyłączamy wspólne czynniki przed nawias.

$a_{n + 1} - a_{n - 1} = a_{1} \cdot {(\frac{1 + \sqrt{5}}{2})}^{n - 2} \cdot [{(\frac{1 + \sqrt{5}}{2})}^{2} - 1]$

Wykonujemy potęgowanie w drugim nawiasie i zapisujemy uzyskane wyrażenie w najprostszej postaci.

$a_{n + 1} - a_{n - 1} = a_{1} \cdot {(\frac{1 + \sqrt{5}}{2})}^{n - 2} \cdot (\frac{1 + \sqrt{5}}{2})$

Mnożymy potęgi o tych samych podstawach – dodajemy wykładniki.

$a_{n + 1} - a_{n - 1} = a_{1} \cdot {(\frac{1 + \sqrt{5}}{2})}^{n - 1}$

Ponieważ $a_{1} \cdot {(\frac{1 + \sqrt{5}}{2})}^{n - 1} = a_{n}$ , zatem:

$a_{n + 1} - a_{n - 1} = a_{n}$

c.n.d

Problemy, w których występują parametry, często są przedstawiane jako zadania „na dowodzenie”. Do ich rozwiązania potrzebne są z reguły wiadomości z różnych działów matematyki. W poniższym przykładzie wykorzystamy znajomość sposobów rozwiązywania układów równań.

Przykład 2

Dany jest układ równań z niewiadomymi $x$ , $y$ , $z$ .

$\{\begin{cases} x + 5 y - z = 5 \\ (- 2 x) + y + z = 6 m \\ x - y + z = 4 m + 1 \end{cases}$

Wykażemy, że istnieją dwie wartości parametru $m$ , dla których rozwiązania $x$ , $y$ , $z$ (w tej kolejności) tego układu równań tworzą ciąg geometrycznyciąg geometrycznyciąg geometryczny.

Sformułowanie założenia i tezy pozostawiamy Ci do samodzielnej pracy, my zaczniemy od dowodu.

Chcemy najpierw znaleźć rozwiązania danego układu równań, nawet gdy rozwiązania będą opisane za pomocą wyrażeń zawierających parametr $m$ .

W tym celu dodajemy stronami pierwsze i drugie równanie układu równań oraz pierwsze i trzecie, aby „wyeliminować” zmienną $z$ .

$\{\begin{cases} x + 5 y - z = 5 \\ (- 2 x) + y + z = 6 m \\ x - y + z = 4 m + 1 \end{cases}$

$\{\begin{cases} (- x) + 6 y = 5 + 6 m \\ 2 x + 4 y = 4 m + 6 \end{cases}$

Mnożymy pierwsze równanie otrzymanego układu przez dwa i dodajemy stronami równania ukladu.

$+ \{\begin{cases} (- 2 x) + 12 y = 10 + 12 m \\ 2 x + 4 y = 4 m + 6 \end{cases}$

Uzyskaliśmy równanie z jedną niewiadomą – wyznaczamy $y$ .

$16 y = 16 m + 16 | : 16$

$y = m + 1$

Wyznaczone wyrażenie podstawiamy w miejsce $y$ do równania $(- x) + 6 y = 5 + 6 m$ .

$\{\begin{cases} y = m + 1 \\ (- x) + 6 y = 5 + 6 m \end{cases}$

$\{\begin{cases} y = m + 1 \\ (- x) + 6 m + 6 = 5 + 6 m \end{cases}$

$\{\begin{cases} y = m + 1 \\ x = 1 \end{cases}$

Powracamy do układu równań z trzema niewiadomymi – dołączając trzecie równie początkowego układu.

$\{\begin{cases} y = m + 1 \\ x = 1 \\ x - y + z = 4 m + 1 \end{cases}$

Obliczamy $z$ .

$\{\begin{cases} y = m + 1 \\ x = 1 \\ 1 - m - 1 + z = 4 m + 1 \end{cases}$

$\{\begin{cases} y = m + 1 \\ x = 1 \\ z = 5 m + 1 \end{cases}$

Rozwiązaniem początkowego układu równań są liczby:

$x = 1$ , $y = m + 1$ , $z = 5 m + 1$ .

O liczbach tych wiemy, że tworzą ciąg geometryczny. Na podstawie zależności między trzema kolejnymi wyrazami ciągu geometrycznego, zapisujemy:

${(m + 1)}^{2} = 1 \cdot (5 m + 1)$

Mamy teraz do rozwiązania równanie kwadratowe z niewiadomą $m$ .

$m^{2} + 2 m + 1 = 5 m + 1$

$m^{2} - 3 m = 0$

$m (m - 3) = 0$

$m = 0$ lub $m = 3$

Dla $m = 0$ otrzymujemy: $x = 1$ , $y = 1$ , $z = 1$ . Liczby te są kolejnymi wyrazami ciągu stałego, a taki ciąg jest ciągiem geometrycznym o ilorazie $1$ .

Dla $m = 3$ otrzymujemy $x = 1$ , $y = 4$ , $z = 16$ . Liczby te są kolejnymi wyrazami ciągu geometrycznego, w którym pierwszy wyraz jest równy $1$ , a iloraz jest równy $4$ .

Zatem istnieją dwie wartości liczby $m$ ( $0$ i $3$ ), spełniające warunki zadania, co należało udowodnić.

Trzeci typ zadań „na dowodzenie” związany z ciągiem geometrycznym, to zadania polegające na udowodnieniu własności sumy kolejnych $n$ początkowych wyrazów ciągu.

Przykład 3

Dany jest skończony ciąg geometryczny $(a_{1}, a_{2}, . . ., a_{n})$ taki, że $q \neq 0$ i $a_{i} \neq 0$ dla $i \in \{1, 2, . . ., n\}$ .

Udowodnimy, że suma odwrotności wszystkich wyrazów tego ciągu jest równa sumie jego wszystkich wyrazów podzielonej przez iloczyn pierwszego i ostatniego wyrazu.

Założenie:

$(a_{1}, a_{2}, . . ., a_{n})$ – ciąg geometryczny

$q \neq 0$ i $a_{i} \neq 0$ dla $i \in \{1, 2, . . ., n\}$

Teza:

$\frac{1}{a_{1}} + \frac{1}{a_{2}} + . . . + \frac{1}{a_{n}} = \frac{S_{n}}{a_{1} \cdot a_{n}}$

Dowód:

Przekształcamy lewą stronę dowodzonej równości, zapisując każdy wyraz ciągu za pomocą pierwszego wyrazu i ilorazu ciągu.

$L = \frac{1}{a_{1}} + \frac{1}{a_{2}} + . . . + \frac{1}{a_{n}} = \frac{1}{a_{1}} + \frac{1}{a_{1} \cdot q} + . . . + \frac{1}{a_{1} \cdot q^{n - 1}}$

Wyłączamy wspólny czynnik, czyli $\frac{1}{a_{1}}$ przed nawias.

$L = \frac{1}{a_{1}} \cdot (1 + \frac{1}{q} + \frac{1}{q^{2}} + . . . + \frac{1}{q^{n - 1}})$

Sprowadzamy ułamki w nawiasie do wspólnego mianownika.

$L = \frac{1}{a_{1}} \cdot (\frac{q^{n - 1} + q^{n - 2} + . . . + q + 1}{q^{n - 1}})$

Rozszerzamy ułamek zapisany w nawiasie przez $a_{1}$ – możemy tak postąpić, bo z założenia wynika, że $a_{1} \neq 0$ .

$L = \frac{1}{a_{1}} \cdot (\frac{a_{1} \cdot q^{n - 1} + a_{1} \cdot q^{n - 2} + \dots + a_{1} \cdot q + a_{1}}{a_{1} \cdot q^{n - 1}})$

W liczniku ułamka znajduje się suma kolejnych $n$ wyrazów ciągu geometrycznego, a w mianowniku wyraz $a_{n}$ .

$L = \frac{1}{a_{1}} \cdot (\frac{S_{n}}{a_{n}})$

$L = \frac{S_{n}}{a_{1} \cdot a_{n}}$

Ostatnia równość dowodzi, że $L = P$ , co należało wykazać.

Teraz odwołamy się do wiadomości dotyczących nie tylko ciągu geometrycznego, ale też arytmetycznego.

Przykład 4

Liczby $b$ , $c$ , $2 b - a$ są kolejnymi wyrazami ciągu geometrycznego. Udowodnimy, że liczby $a b$ , $b^{2}$ , $c^{2}$ są kolejnymi wyrazami ciągu arytmetycznego.

Założenie:

$(b, c, 2 b - a)$ – ciąg geometrycznyciąg geometrycznyciąg geometryczny

Teza:

$(a b, b^{2}, c^{2})$ – ciąg arytmetyczny

Dowód:

Z własności ciągu geometrycznego wynika, że

$c^{2} = b (2 b - a)$

Przekształcamy otrzymane wyrażenie.

$c^{2} = 2 b^{2} - a b$

Wyznaczamy $b^{2}$ .

$2 b^{2} = c^{2} + a b | : 2$

$b^{2} = \frac{c^{2} + a b}{2}$

Otrzymana równość oznacza, że liczba $b^{2}$ jest średnią arytmetyczną liczb $a b$ i $c^{2}$ .

Dowodzi to, że ciąg $(a b, b^{2}, c^{2})$ jest arytmetyczny.

Ostatni przykład pokazuje związek ciągu geometrycznego z geometrią.

Przykład 5

Boki $a$ , $b$ , $c$ trójkąta $A B C$ i wysokość $h$ opuszczona na bok $a$ , tak jak na rysunku, tworzą ciąg geometryczny. Udowodnimy, że trójkąt $A B C$ jest prostokątny.

R4p2PhjhUOEAC

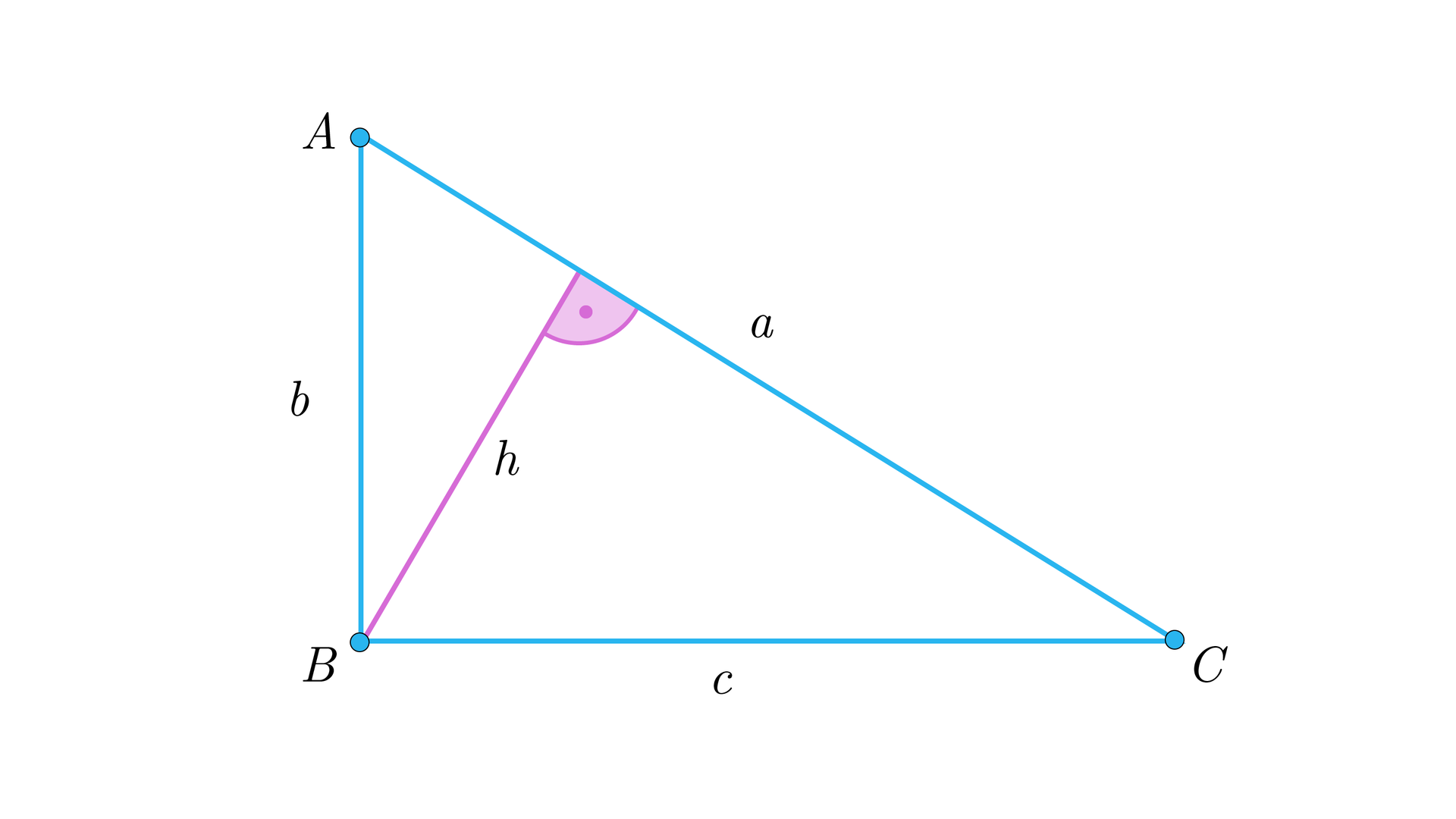
Rysunek przedstawia trójkąt prostokątny o podstawie c, która jest jednocześnie bokiem BC, o pionowej przyprostokątnej b, która jest bokiem AB oraz o przeciwprostokątnej a, która jest bokiemCA. Z wierzchołka przy kącie prostym, czyli wierzchołka B poprowadzono do przeciwprostokątnej wysokość h i oznaczono między nimi kąt prosty.

Założenie:

$(a, b, c, h)$ – ciąg geometryczny

$a > 0$ , $b > 0$ , $c > 0$ , $h > 0$

Teza:

Trójkąt $A B C$ jest prostokątny.

Dowód:

Z zależności między wyrazami ciągu geometrycznego wynika równość:

$\frac{b}{a} = \frac{h}{c}$

Czyli:

$a h = b c$

Mnożymy obie strony równości przez $\frac{1}{2}$ .

$\frac{1}{2} a h = \frac{1}{2} b c$

Lewa strona zapisanej równości opisuje pole trójkąta $A B C$ .

$P = \frac{1}{2} a h$

Pole tego trójkąta można też obliczyć w nieco inny sposób – znając długości jego dwóch boków i miarę kata między tymi bokami.

Oznaczmy przez $α$ miarę kąta $A B C$ . Wtedy

$P = \frac{1}{2} b c \sin α$

Porównujemy otrzymane wyrażenia.

$\frac{1}{2} a h = \frac{1}{2} b c \sin α$

Ponieważ

$\frac{1}{2} a h = \frac{1}{2} b c$

zatem $\frac{1}{2} b c \sin α = \frac{1}{2} b c$ .

Stąd wynika, że $\sin α = 1$ , czyli $α = 90 °$ .

Trójkąt $A B C$ jest więc trójkątem prostokątnym, co należało wykazać.

Słownik

ciąg geometryczny

ciągiem geometrycznym nazywamy ciąg liczbowy co najmniej trzywyrazowy, w którym każdy wyraz, począwszy od drugiego, powstaje przez pomnożenie wyrazu poprzedniego przez liczbę $q$ , zwaną ilorazem ciągu

Wprowadzenie

Galeria zdjęć interaktywnych

Słownik