Przeczytaj
Każdemu zdarzeniu możemy przyporządkować liczbę (przy ustalonym zdarzeniu takim, że ). Liczbę tę nazywamy prawdopodobieństwem warunkowym zajścia zdarzenia , pod warunkiem, że zaszło zdarzenie .
Niech i oraz niech . Prawdopodobieństwem zajścia zdarzenia , pod warunkiem, że zaszło zdarzenie , nazywamy liczbę
Z definicji prawdopodobieństwa warunkowego wynika, że . Ponieważ dla każdych zdarzeń elementarnych i spełniony jest warunek , więc .
Zauważmy też, że z warunku i wynika, że . Wykazaliśmy zatem, że jeśli to dla każdego zdarzenia spełniona jest nierówność podwójna .
W ten sposób wykazaliśmy jedną z własności prawdopodobieństwa warunkowego. Tę i inne własności zawieramy w poniższym twierdzeniu.
Niech będzie dowolna przestrzenią zdarzeń elementarnych oraz niech , , i . Wtedy:
jeśli to
jeśli to
Zastosowanie tych własności pokażemy, rozwiązując problemy zawarte w poniższych przykładach.
W jednym rzędzie stoi dziesięć stolików. Każdy z dziesięciu maturzystów losuje numer stolika. Oblicz prawdopodobieństwo tego, że Grażyna i Ewa nie będą siedziały obok siebie, gdy wiemy, że Ewa wylosowała stolik numer cztery.
Oznaczmy:
– zdarzenie polegające na ty, że Grażyna i Ewa nie będą siedziały obok siebie,
– zdarzenie polegające na tym, że Ewa wylosowała stolik numer cztery.

Obliczymy najpierw .
Zdarzeniu sprzyjają losowania, w wyniku których Ewa i Grażyna wylosują sąsiednie stoliki.
Zatem Ewa usiądzie przy stoliku numer cztery, a Grażyna przy stoliku numer trzy lub pięć.
Pozostałe osiem osób może usiąść w dowolny sposób na ośmiu pozostałych miejscach.
Zdarzeniu sprzyjają wszystkie permutacje zbioru dziewięcioelementowego (dziewięciu uczniów zajmuje w dowolny sposób miejsc różnych od miejsca oznaczonego numerem – bo tam już usiądzie Ewa).
Stąd
Korzystając z własności prawdopodobieństwa warunkowegowłasności prawdopodobieństwa warunkowego, zapisujemy:
Odpowiedź:
Prawdopodobieństwo tego, że Ewa i Grażyna nie będą siedziały obok siebie jest równe .
Niech i .
Wykażemy, że jeśli to .
Ponieważ i , więc
.
Rzucamy cztery razy monetą. Obliczymy prawdopodobieństwo uzyskania dodatniej, parzystej liczby reszek jeżeli wiadomo, że za drugim razem wyrzucono orła.
Oznaczmy:
– zdarzenie polegające na wyrzuceniu parzystej liczby reszek,
– zdarzenie polegające na tym, że w drugim rzucie wypadł orzeł.
Liczbę wszystkich zdarzeń elementarnych obliczymy jako liczbę czterowyrazowych wariacji z powtórzeniami zbioru dwuelementowego.
Zdarzeniu sprzyja siedem zdarzeń:
Zdarzeniu sprzyja osiem zdarzeń elementarnych:
Zatem
Obliczamy prawdopodobieństwo uzyskania parzystej liczby reszek, pod warunkiem że za drugim razem wyrzucono orła.
Odpowiedź:
Prawdopodobieństwo uzyskania parzystej liczby reszek, pod warunkiem że za drugim razem wyrzucono orła jest równe .
Ze wzoru na prawdopodobieństwo warunkowe wynika poniższy wniosek.
Wniosek:
Niech będzie dowolną przestrzenią zdarzeń elementarnych oraz niech , i . Wtedy:
Z urny, w której znajduje się kul niebieskich i czarne losujemy po kolei dwie kule bez zwracania. Obliczymy prawdopodobieństwo tego, że wylosujemy kule w kolejności: czarna, niebieska.
Oznaczmy:
– zdarzenie polegające na tym, że za pierwszym razem wylosowano kulę czarną,
– zdarzenie polegające na tym, że za drugim razem wylosowano kulę niebieską.
Należy obliczyć prawdopodobieństwo zdarzenia .
Początkowo w urnie było kul, w tym czarne. Zatem prawdopodobieństwo wylosowania kuli czarnej było równe . Gdy wylosowano jedną kulę – zostało tylko kul, w tym niebieskich. Wtedy prawdopodobieństwo wylosowania z urny kuli niebieskiej było równe .
Przedstawimy graficznie sytuację opisaną w zadaniu.
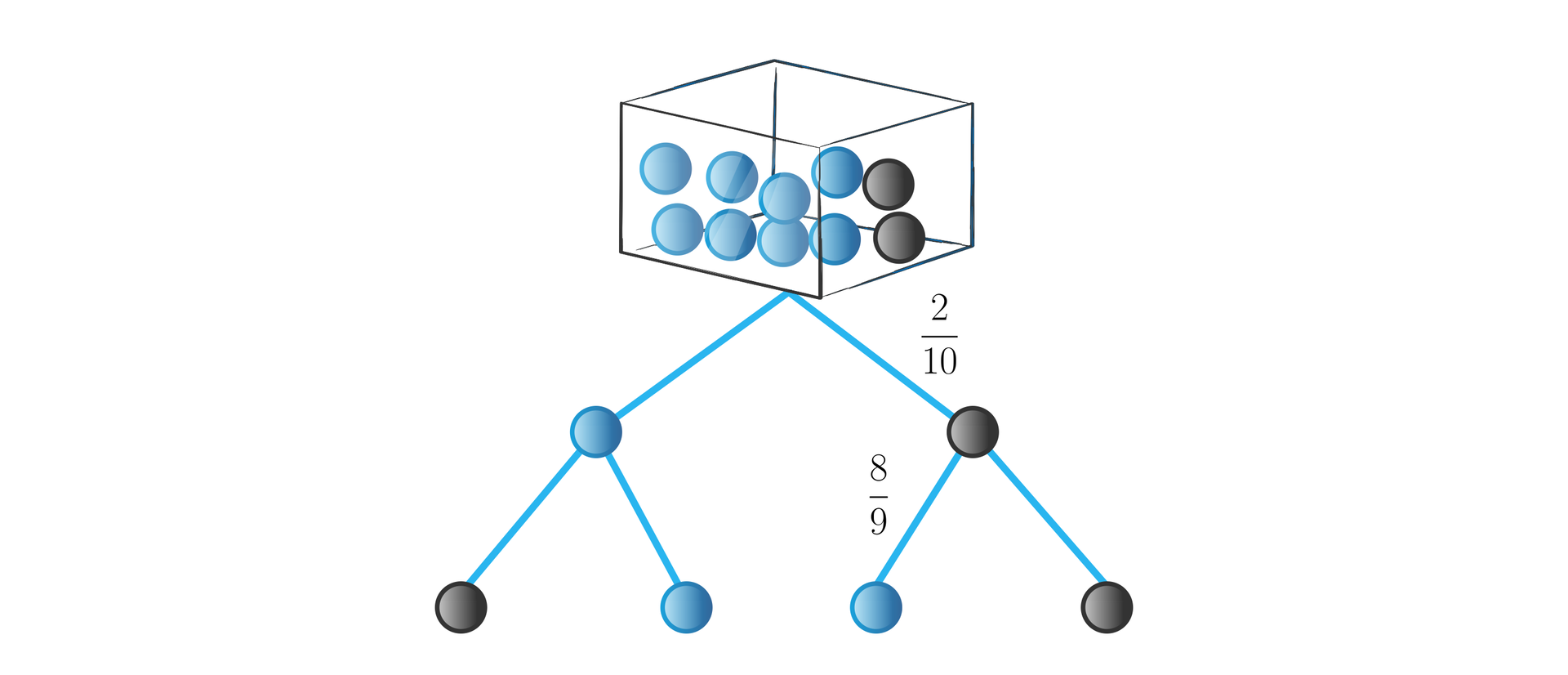
Korzystamy z poznanego wzoru:
Odpowiedź:
Prawdopodobieństwo tego, że wylosujemy kule w kolejności: czarna, niebieska jest równe .
Z talii kart losujemy kolejno trzy karty. Obliczymy, prawdopodobieństwo tego, że każda karta będzie w innym kolorze.
Oznaczmy:
– zdarzenie polegające na tym, że druga karta jest innego koloru niż pierwsza,
– zdarzenie polegające na tym, że trzecia wylosowana karta jest w innym kolorze niż pierwsza i druga.
Pierwszą kartę wylosowaliśmy spośród , ale drugą już spośród . Jednak możliwości wyboru, aby nie była tego samego koloru co pierwsza jest .
Trzecią kartę losujemy spośród pozostałych kart. Dwa kolory kart są już „zajęte” zatem na wylosowanie karty w innym kolorze niż karta pierwsza oraz druga pozostaje możliwości.
Obliczamy prawdopodobieństwo iloczynu zdarzeń i
Odpowiedź:
Prawdopodobieństwo tego, że każda karta będzie w innym kolorze jest równe .
Słownik
niech będzie dowolna przestrzenią zdarzeń elementarnych oraz niech , , i ; wtedy:
jeśli to
jeśli to