Wykażemy, że w dowolnym trójkącie prostokątnym o kątach ostrych $\alpha$ i $\beta$ zachodzi zależność: $\sin \alpha +\sin \beta >1$.

Rozwiązanie

Naszkicujmy trójkąt prostokątny oraz wprowadźmy oznaczenia:

RVOCCDTUAceuX

Rysunek przedstawia trójkąt prostokątny o podstawie $a$, która jest jednocześnie bokiem $CB$, o pionowej przyprostokątnej $b$, która jest bokiem $AC$ oraz o przeciwprostokątnej $c$, która jest bokiem $AB$. Na ilustracji zaznaczono kąty wewnętrze trójkąta. Przy wierzchołku $C$ znajduje się kąt prosty, przy wierzchołku $B$ znajduje się kąt $\beta$, a przy wierzchołku $A$ znajduje się kąt $\alpha$.

Z definicji funkcji trygonometrycznych mamy, że:

$\sin \alpha =\frac{a}{c}$ oraz $\sin \beta =\frac{b}{c}$.

Podstawiamy te wyrażenia do nierówności. Otrzymujemy, że:

$\sin \alpha +\sin \beta =\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$.

Z nierówności trójkąta wynika, że $a+b>c$.

Zatem $\sin \alpha +\sin \beta =\frac{a+b}{c}>\frac{c}{c}=1$.

Udowodnimy następującą tożsamość trygonometrycznątożsamość trygonometrycznatożsamość trygonometryczną: $\frac{1+{\displaystyle \frac{\sin \alpha }{\cos \alpha }}}{1+{\displaystyle \frac{\cos \alpha }{\sin \alpha }}}=\mathrm{tg}\alpha$, gdzie $\alpha \ne \frac{k\pi }{2}$ oraz $k\in \mathrm{\mathbb{Z}}$.

Rozwiązanie

Wychodząc od lewej strony tej tożsamości, mamy:

$\frac{1+{\displaystyle \frac{\sin \alpha }{\cos \alpha }}}{1+{\displaystyle \frac{\cos \alpha }{\sin \alpha }}}=\frac{{\displaystyle \frac{\cos \alpha }{\cos \alpha }+\frac{\sin \alpha }{\cos \alpha }}}{{\displaystyle \frac{\sin \alpha }{\sin \alpha }+\frac{\cos \alpha }{\sin \alpha }}}=\frac{{\displaystyle \frac{\cos \alpha +\sin \alpha }{\cos \alpha }}}{{\displaystyle \frac{\sin \alpha +\cos \alpha }{\sin \alpha }}}=$

$=\frac{\cos \alpha +\sin \alpha }{\cos \alpha }·\frac{\sin \alpha }{\sin \alpha +\cos \alpha }=\frac{\sin \alpha }{\cos \alpha }=\mathrm{tg}\alpha$.

Obliczymy wartość wyrażenia $\frac{\sin 6°·\cos 726°}{\sin 1086°·\cos 6°+\sin 366°·\cos 1086°}$.

Rozwiązanie

Korzystając z tego, że funkcje trygonometryczne są okresowe, wyrażenie możemy zapisać w postaci:

$\frac{\sin 6°·\cos 6°}{\sin 6°·\cos 6°+\sin 6°·\cos 6°} =\frac{\sin 6°·\cos 6°}{2\sin 6°·\cos 6°}=\frac{1}{2}$.

Wskażemy liczbę mniejszą wśród liczb $\sin 5°$ oraz $\mathrm{tg}5°$.

Rozwiązanie

Zbadamy znak różnicy $\sin 5°-\mathrm{tg}5°$.

Otrzymujemy:

$\sin 5°-\mathrm{tg}5°=\sin 5°-\frac{\sin 5°}{\cos 5°}=\frac{\sin 5°\cos 5°}{\cos 5°}-\frac{\sin 5°}{\cos 5°}=\frac{\sin 5°\left(\cos 5°-1\right)}{\cos 5°}$.

Ponieważ $\sin 5°>0$ oraz $0<\cos 5°<1$, więc $\cos 5°-1<0$.

Zatem liczba $\sin 5°-\mathrm{tg}5°$ jest ujemna, co oznacza, że $\sin 5°<\mathrm{tg}5°$.

Pokażemy, że wartość wyrażenia $\frac{\sin \alpha }{1-\cos \alpha }+\frac{\sin \alpha }{1+\cos \alpha }$ dla $\alpha =30°$ wynosi $4$.

Rozwiązanie

Sprowadzając wyrażenia do wspólnego mianownika, otrzymujemy:

$\frac{\sin \alpha }{1-\cos \alpha }+\frac{\sin \alpha }{1+\cos \alpha }=\frac{\sin \alpha \left(1+\cos \alpha \right)}{\left(1-\cos \alpha \right)\left(1+\cos \alpha \right)}+\frac{\sin \alpha \left(1-\cos \alpha \right)}{\left(1-\cos \alpha \right)\left(1+\cos \alpha \right)}=$

$=\frac{\sin \alpha +\sin \alpha \cos \alpha }{\left(1-\cos \alpha \right)\left(1+\cos \alpha \right)}+\frac{\sin \alpha -\sin \alpha \cos \alpha }{\left(1-\cos \alpha \right)\left(1+\cos \alpha \right)}=\frac{2\sin \alpha }{1-{\cos }^2\alpha }=\frac{2\sin \alpha }{{\sin }^2\alpha }=\frac{2}{\sin \alpha }$.

Wartość wyrażenia $\frac{2}{\sin \alpha }$ dla $\alpha =30°$ wynosi:

$\frac{2}{\sin 30°}=\frac{2}{{\displaystyle \frac{1}{2}}}=4$.

Udowodnimy następującą tożsamość trygonometryczną: $\frac{2}{{\cos }^2\alpha }-2=2{\mathrm{tg}}^2\alpha$.

Rozwiązanie

Wychodząc od lewej strony tożsamości, mamy

$\frac{2}{{\cos }^2\alpha }-2=\frac{2}{{\cos }^2\alpha }-\frac{2{\cos }^2\alpha }{{\cos }^2\alpha }=\frac{2-2{\cos }^2\alpha }{{\cos }^2\alpha }=\frac{2\left(1-{\cos }^2\alpha \right)}{{\cos }^2\alpha }=$

$=\frac{2{\sin }^2\alpha }{{\cos }^2\alpha }=2{\mathrm{tg}}^2\alpha$.

Wykażemy, że w dowolnym trójkącie prostokątnym o przyprostokątnych $a$ i $b$, przeciwprostokątnej $c$, kącie ostrym $\alpha$, długość przeciwprostokątnej $c$ możemy obliczyć ze wzoru $c=\frac{2r}{\sin \alpha +\cos \alpha -1}$, jeżeli $r$ jest promieniem okręgu wpisanego w ten trójkąt.

R1XVk7NzAZiLL

Rysunek przedstawia trójkąt prostokątny o podstawie $a$, która jest jednocześnie bokiem $CB$, o pionowej przyprostokątnej $b$, która jest bokiem $AC$ oraz o przeciwprostokątnej $c$, która jest bokiem $BA$. Na ilustracji zaznaczono kąty wewnętrze trójkąta. Przy wierzchołku $C$ znajduje się kąt prosty, przy wierzchołku $B$ znajduje się kąt $\beta$, a przy wierzchołku $A$ znajduje się kąt $\alpha$.

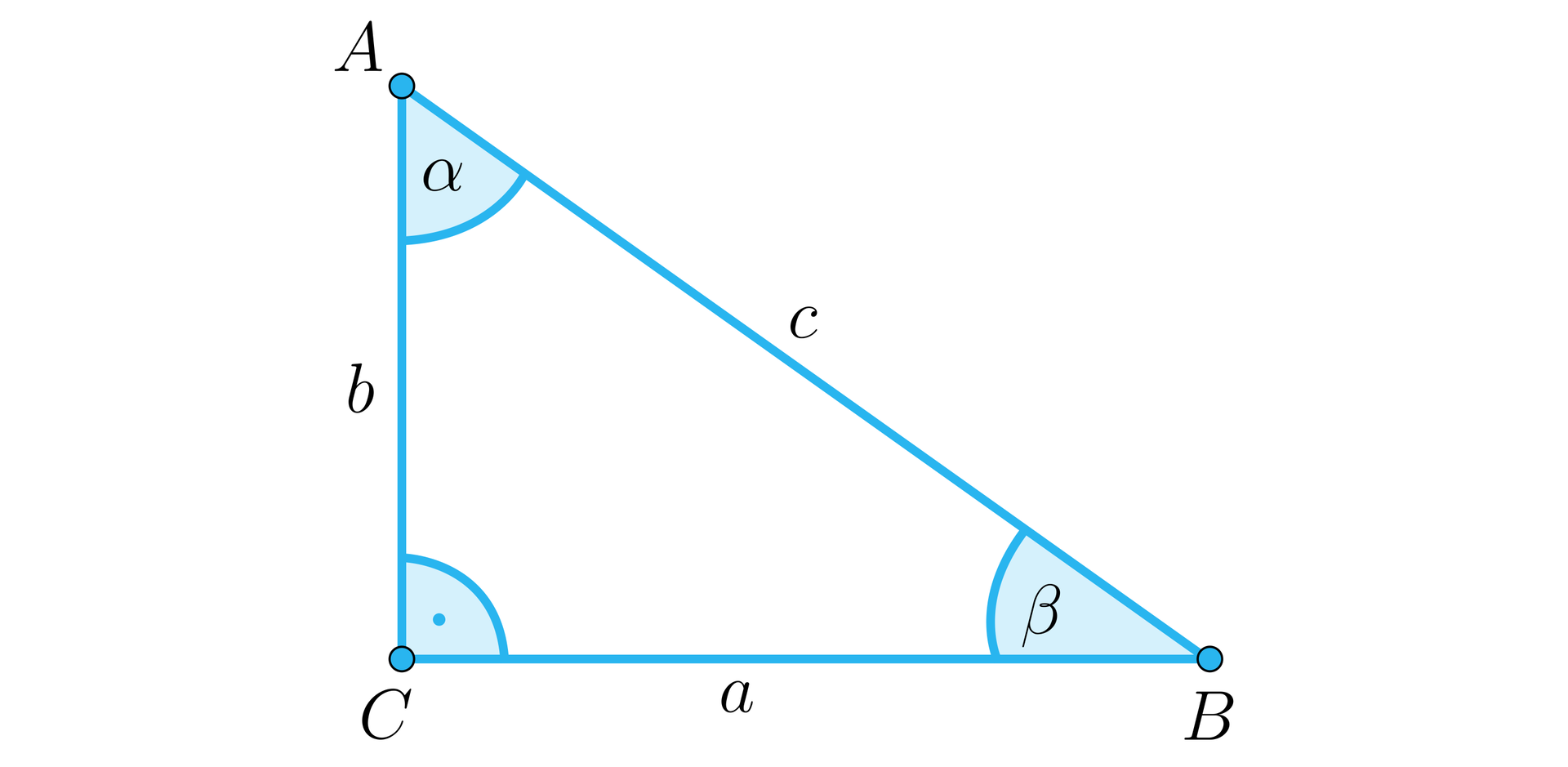
Rozwiązanie

W dowodzie wykorzystamy wzór na promień $r$ okręgu wpisanego w trójkąt prostokątny o przyprostokątnych $a$ i $b$ oraz przeciwprostokątnej $c$:

$r=\frac{a+b-c}{2}$.

Z definicji funkcji trygonometrycznych w trójkącie prostokątnym mamy, że:

$\sin \alpha =\frac{a}{c}$, więc $a=c\sin \alpha$,

$\cos \alpha =\frac{b}{c}$, więc $b=c\cos \alpha$.

Po podstawieniu do wzoru na $r$ otrzymujemy, że $r=\frac{c\sin \alpha +c\cos \alpha -c}{2}=\frac{c\left(\sin \alpha +\cos \alpha -1\right)}{2}$.

Po przekształceniu wzór jest postaci: $c=\frac{2r}{\sin \alpha +\cos \alpha -1}$.

podstawowa zależność pomiędzy funkcjami trygonometrycznymi