Przeczytaj
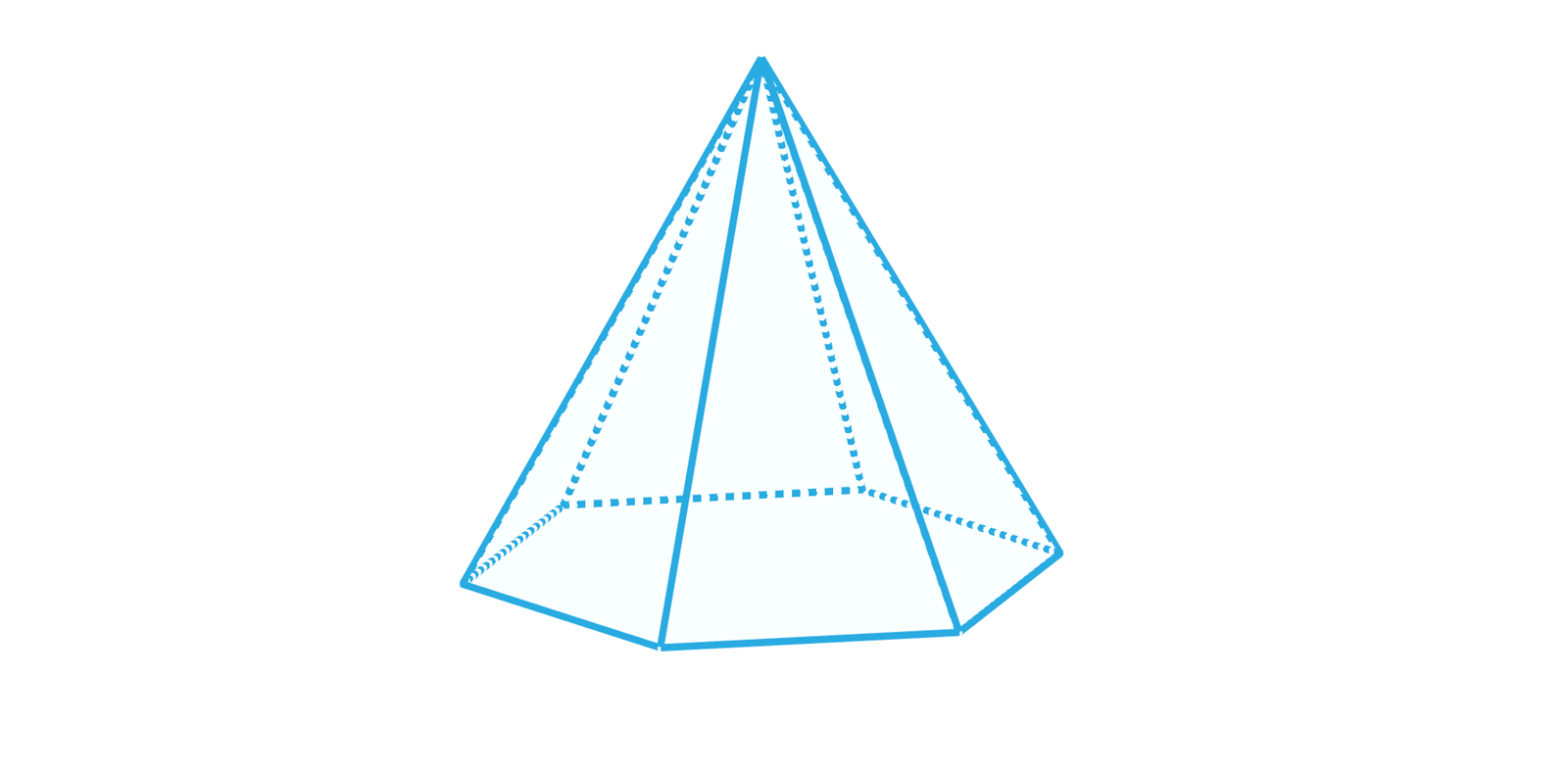
Ostrosłup prawidłowyOstrosłup prawidłowy sześciokątny to ostrosłup prostyostrosłup prosty, który ma w podstawie sześciokąt foremny, a ściany boczne są przystającymi trójkątami równoramiennymi. Zauważ, że ostrosłup prawidłowy sześciokątny ma:
podstawę,
ścian, w tym ścian bocznych, które są trójkątami równoramiennymi,
wierzchołków,
krawędzi ( krawędzi bocznych i krawędzi podstawy).

Pokażemy, że dla ostrosłupa prawidłowego sześciokątnego zachodzi twierdzenie Euleratwierdzenie Eulera dla wielościanów wypukłych:
zatem:
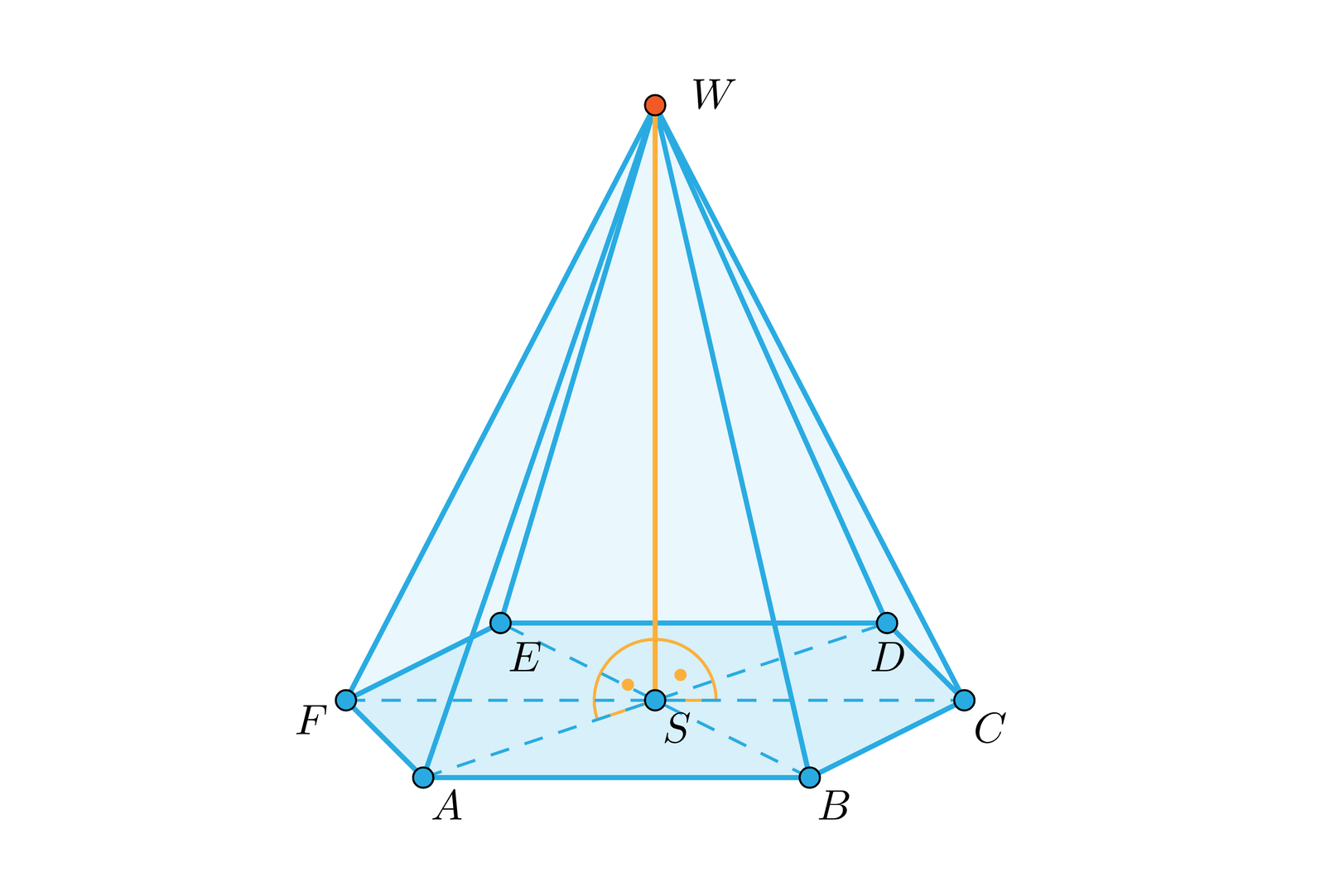
Spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego i wpisanego w sześciokąt foremny, leży więc na przecięciu dłuższych przekątnych sześciokąta foremnego.
Kąty nachylenia wszystkich ścian bocznych ostrosłupa prawidłowego sześciokątnego do płaszczyzny podstawy są równe.
Poniższy aplet pozwoli Ci zobaczyć, jak zachowuje się nasza bryła. Przesuń suwaki i zobacz, jak wygląda ostrosłup prawidłowy sześciokątnyostrosłup prawidłowy sześciokątny.
Zapoznaj się z poniższym apletem przedstawiającym ostrosłup prawidłowy sześciokątny.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DjTjnefwk
Przyjrzymy się teraz, w jaki sposób narysować ostrosłup prawidłowy sześciokątny.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DjTjnefwk
Zapoznaj się ze sposobem rysowania ostrosłupa sześciokątnego.
W pierwszym kroku rysujemy rzut sześciokąta foremnego i zaznaczamy punkt przecięcia się jego dłuższych przekątnych. Wierzchołki narysowanego sześciokąta można oznaczyć jako A B C D E F, natomiast punkt przecięcia się dłuższych przekątnych można podpisać literą S. W kolejnym kroku rysujemy prostą prostopadłą do płaszczyzny podstawy, która przechodzi przez punkt S, na prostej zaznaczamy punkt W, który musi być różny od punktu S. Kolejno tworzymy odcinki AW, BW, CW, DW, EW oraz FW. Otrzymujemy w ten sposób rzut ostrosłupa prawidłowego sześciokątnego na płaszczyznę.
Narysujemy siatkę ostrosłupa prawidłowego szesćiokątnego o krawędzi podstawy długości i krawędzi bocznej długości
Rozwiązanie
Rysujemy najpierw sześciokąt foremny o krawędzi długości . Na każdym jego boku budujemy trójkąt równoramienny o podstawie oraz ramieniu długości .

Sprawdzimy, czy z odcinków długości i da się zbudować ostrosłup prawidłowy sześciokątny o krawędzi podstawy i krawędzi bocznej .
Rozwiązanie
Zauważmy, że dłuższa przekątna podstawy ostrosłupa prawidłowego sześciokątnego i przeciwległe krawędzie tworzą trójkąt, co widać na poniższym rysunku:
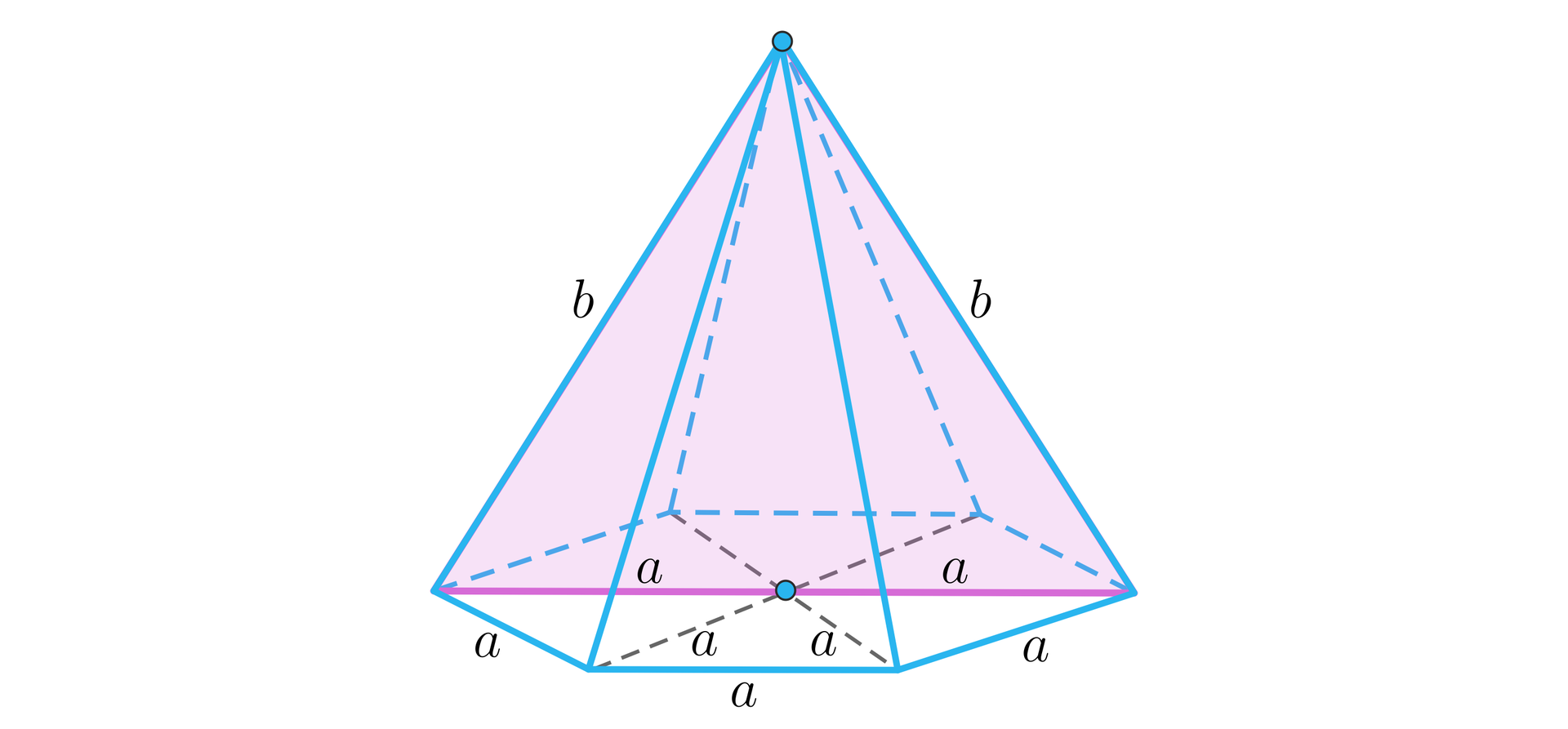
Z warunku trójkąta wynika, że długość każdego boku tego trójkąta musi być mniejsza niż suma długości pozostałych boków. Podstawą tego trójkąta jest przekątna sześciokąta, której długość wynosi . Suma długości pozostałych boków jest równa , co jest sprzeczne z warunkiem trójkąta. Zatem z odcinków długości i nie da się zbudować ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy i krawędzi bocznej .
Długość krawędzi bocznej ostrosłupa prawidłowego sześciokątnego musi być większa od długości krawędzi jego podstawy.
Suma długości krawędzi ostrosłupa prawidłowego sześciokątnego wynosi . Obliczymy długości tych krawędzi wiedząc, że krawędzie boczne są dwa razy dłuższe od krawędzi podstawy.
Rozwiązanie
Wiemy, że omawiany ostrosłup ma krawędzi podstawy (oznaczmy je jako ) i sześć krawędzi bocznych (). Powstaje równanie:
,
,
,
.
Zatem krawędź podstawy ostrosłupa prawidłowego sześciokątnego ma długość a krawędź boczna ma długość .
Suma długości krawędzi ostrosłupa prawidłowego sześciokątnego, w którym krawędź boczna jest cztery razy dłuższa od krawędzi podstawy, wynosi . Obliczymy pole podstawy tego ostrosłupa.
Rozwiązanie
Oznaczmy długość krawędzi podstawy jako niewiadomą . Krawędź boczna jest cztery razy dłuższa, czyli ma długość . Możemy więc ułożyć równanie:
,
,
,
.
Obliczymy pole podstawy naszego ostrosłupa, czyli pole sześciokąta foremnego.
Drut o długości wykorzystano do stworzenia modelu ostrosłupa prawidłowego sześciokątnego. Podzielono go w stosunku . Dłuższą część wykorzystano na krawędzie boczne, krótszą na krawędzie podstawy. Obliczymy długość poszczególnych krawędzi ostrosłupa oraz cosinus kąta nachylenia krawędzi bocznej do krawędzi podstawy.
Rozwiązanie
Drut podzielono na części,
co oznacza, że suma długości krawędzi bocznych ostrosłupa wynosi , zaś suma krawędzi podstawy: . Policzmy więc długości poszczególnych krawędzi: - długość krawędzi bocznej - długość krawędzi podstawy.
Wykonajmy rysunek pomocniczy, aby zobaczyć, jak policzyć cosinus kąta nachylenia krawędzi bocznej do krawędzi podstawy. Oznaczmy go .

Dłuższa przekątna podstawy ostrosłupa prawidłowego sześciokątnego ma długość . Krawędź boczna jest dłuższa od krawędzi podstawy o . Obliczymy sumę długości krawędzi tego ostrosłupa oraz miarę kąta płaskiego przy wierzchołku ostrosłupakąta płaskiego przy wierzchołku ostrosłupa.
Rozwiązanie
Zacznijmy od policzenia długości krawędzi podstawy naszego ostrosłupa. Skoro przekątna podstawy ma długość , to korzystając ze wzoru na dłuższą przekątną podstawy otrzymujemy:
,
co daje nam:
.
Krawędź boczna jest dłuższa o , więc ma długość . Policzmy więc sumę krawędzi naszego ostrosłupa:
.
Wykonajmy rysunek pomocniczy.

Obliczmy miarę kąta płaskiego przy wierzchołku ostrosłupa. Skorzystajmy z twierdzenia cosinusów.
Słownik
ostrosłup prosty, którego podstawa jest wielokątem foremnym
ostrosłup, którego wszystkie krawędzie boczne są równe. Spodek wysokości ostrosłupa prostego jest środkiem okręgu opisanego na podstawie.
ostrosłup prosty, którego podstawa jest sześciokątem foremny
kąt pomiędzy ramionami ściany bocznej ostrosłupa
opisuje zależność pomiędzy liczbą wierzchołków, ścian i krawędzi wielościanu: , gdzie: - liczba wierzchołków, - liczba ścian, - liczba krawędzi.