Przeczytaj

Zanim zdefiniujemy pojęcie wycinka koła, zacznijmy od prostego przykładu z życia codziennego.

Załóżmy, że mamy pizzę, która jest pokrojona w standardowy sposób na $8$ równych części.

R1akKOAo7pGo6

Ilustracja przedstawia pizzę pokrojoną na osiem równych kawałków.

Pole pojedynczego kawałka stanowi więc $\frac{1}{8}$ całości pola pizzy. Załóżmy, że promień naszego placka wynosi $r$ . Wówczas cała pizza ma pole

P = π r^{2}

Pole każdego z kawałków wynosi więc

P_{k} = \frac{1}{8} π r^{2}

Co w sytuacji, gdy kawałki nie są równe? Rozważmy następującą sytuację:

R1b5MJ5oeJZoX

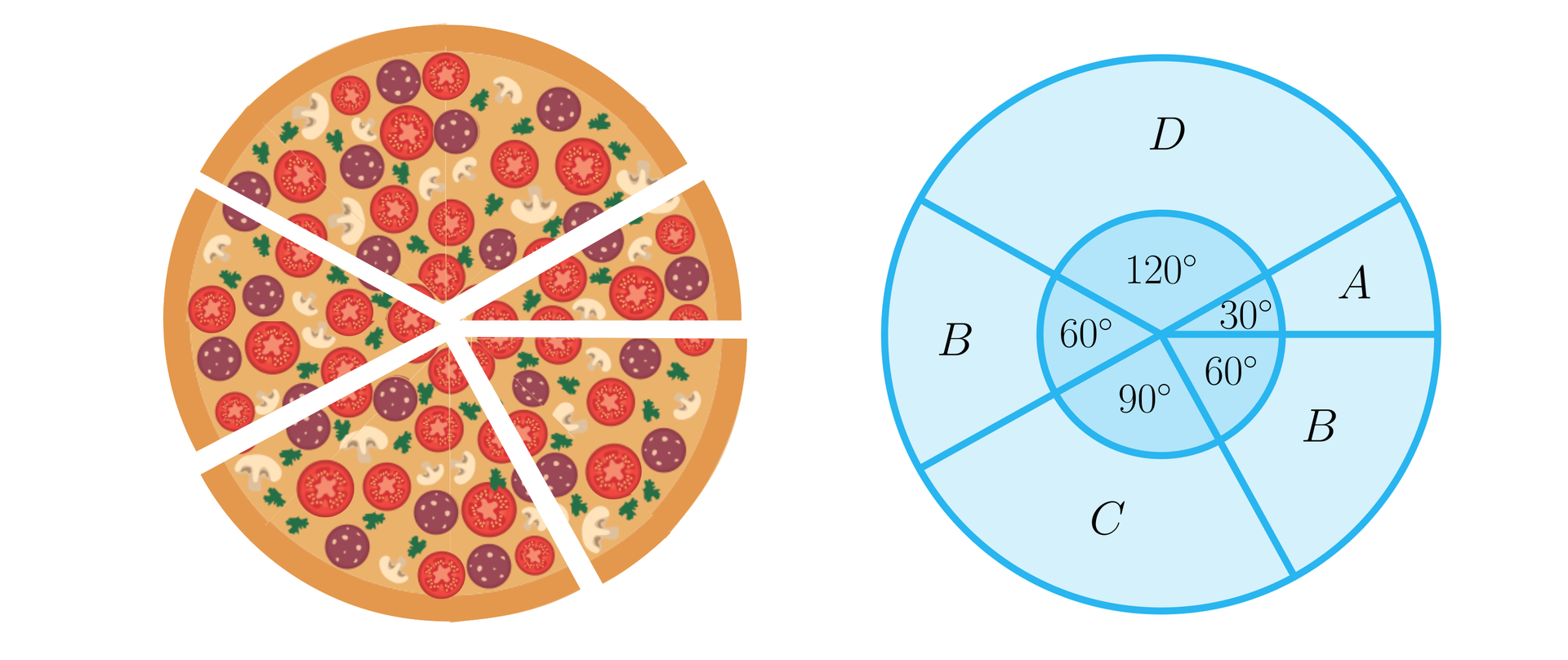
Ilustracja przedstawia pizzę pokrojoną na 5 różnej wielkości kawałków, przy czym wszystkie kawałki wykrojone są od środka. Obok pizzy narysowano schemat przekroju pizzy, czyli koło, w którym wykreślono 5 wycinków: wycinek A ma kąt 30 stopni, wycinek B ma 60 stopni, wycinek C ma 90 stopni, wycinek C ma 90 stopni, wycinek B ma 60 stopni i wycinek D ma 120 stopni.

Rzadko kiedy mamy do czynienia z tak nierównym podziałem. Zauważmy jednak, że każdy z tych kawałków pizzy stanowi fragment koła, który wyznaczony jest przez pewien kąt środkowykąt środkowykąt środkowy. Ramiona tego kąta przecinają brzeg koła w dwóch punktach, wycinając pewien fragment okręgu (który nazywany jest zwykle łukiem). W ten sposób dochodzimy do definicji wycinka koła.

Wycinek koła

Definicja: Wycinek koła

Wycinkiem koła nazywamy część koła ograniczoną przez ramiona kąta środkowego i łukłuk okręgułuk oparty na tym samym kącie.

Zaobserwować możemy, że istnieje bezpośredni związek pomiędzy miarą kąta środkowego odpowiadającego fragmentowi pizzy, a polem powierzchni tego kawałka. Istotnie, stosunek pola powierzchni wycinka do pola całego koła jest taki sam, jak stosunek kąta środkowego odpowiadającego owemu wycinkowi do kąta pełnegokąt pełnykąta pełnego.

Zatem wycinek koła o promieniu $r$ , który jest oparty na kącie prostym (stanowiącym $\frac{1}{4}$ kąta pełnego) będzie miał pole równe $\frac{1}{4} π r^{2}$ . Analogicznie, wycinek oparty o kąt $60 °$ będzie miał pole powierzchni stanowiące $\frac{60 °}{360 °} = \frac{1}{6}$ pola powierzchni całego koła.

Obserwację tę możemy zapisać w formie następującego twierdzenia.

Pole powierzchni wycinka koła

Twierdzenie: Pole powierzchni wycinka koła

Pole wycinka koła o promieniu $r$ i kącie środkowym $α$ wyrażonym w stopniach wyrażone jest wzorem:

P = \frac{α}{360 °} \cdot π r^{2}

Gdzie możemy zastosować wzór na pole wycinka koła?

Wróćmy do naszej przykładowej pizzy (ma ona średnicę $42 cm$ ). Promień tej pizzy to $r = 21 cm$ . Obliczmy pole powierzchni każdego z kawałków:

najmniejszy kawałek wyznaczany jest przez kąt środkowykąt środkowykąt środkowy $30 °$ i ma on pole
$P_{30 °} = \frac{30 °}{360 °} \cdot π \cdot {(21 cm)}^{2} = \frac{441}{12} π {cm}^{2}$
średnie fragmenty oparte są o kąt środkowy o mierze $60 °$ . Ich pole powierzchni wynosi
$P_{60 °} = \frac{60 °}{360 °} \cdot π \cdot {(21 cm)}^{2} = \frac{441}{6} π {cm}^{2}$
duża porcja, odpowiadająca kątowi środkowemu $90 °$ ma pole powierzchni równe
$P_{90 °} = \frac{90 °}{360 °} \cdot π \cdot {(21 cm)}^{2} = \frac{441}{4} π {cm}^{2}$
największa część wyznaczana jest przez kąt środkowy $120 °$ , zaś jej pole powierzchni jest równe
$P_{120 °} = \frac{120 °}{360 °} \cdot π \cdot {(21 cm)}^{2} = \frac{441}{3} π {cm}^{2}$

Wzór na pole wycinka koła pozwala nam obliczać pola nietypowych figur, które można przedstawić przy pomocy mniejszych części.

pierścień kołowy

Definicja: pierścień kołowy

Pierścień kołowypierścień kołowyPierścień kołowy to figura płaska, która jest fragmentem płaszczyzny ograniczonym przez dwa okręgi współśrodkowe o różnych promieniach.

Pole powierzchni pierścienia kołowego jesteśmy w stanie wyznaczyć odejmując od siebie pola dwóch okręgów, które go tworzą. I – analogicznie jak w przypadku wycinka kołowego – stosunek kąta odpowiadającemu danemu wycinkowi pierścienia kołowego do kąta pełnego jest taki sam, jak stosunek pola powierzchni wycinka do pola powierzchni całego pierścienia. Mamy zatem twierdzenie:

o polu powierzchni pierścienia kołowego

Twierdzenie: o polu powierzchni pierścienia kołowego

Pole pierścienia kołowego o zewnętrznym promieniu $R$ i wewnętrznym $r$ wynosi:

P_{p} = π (R^{2} - r^{2})

Pole wycinka tego pierścienia opartego na kącie środkowym $α$ wynosi:

P_{w} = \frac{α}{360 °} \cdot π \cdot (R^{2} - r^{2})

Wyliczanie pola wycinka pierścienia kołowego często przydaje się w życiu codziennym

Przykład 1

Poniższy rysunek obrazuje drogę dojazdową do gospodarstwa państwa Kowalskich. Przyjmijmy, że droga ma w każdym miejscu taką samą szerokość oraz że $E F ∥ G H$ i $A B ∥ C D$

RkSiub9VzV95f

Ilustracja przedstawia schematyczną drogę, która skręca. Od góry po lewej mamy poziomy odcinek A B o długości 4, jest to początek drogi. Jej początkowy kawałek biegnie pionowo w dół rysunku i jest w kształcie prostokąta A B C D, gdzie krawężniki A C oraz B D ma długość 5 każdy. Punkty C i D leżące po przeciwnej stronie drogi połączono odcinkiem. Z punktu D poprowadzono łuk w dół i w prawo do punktu E. Łuk ten jest ćwiartką okręgu o promieniu 3 i środku w punkcie S, narysowano też promienie D S oraz E S. Analogicznie po przeciwnej stronie drogi zaznaczono z punktu C do F drugi łuk biegnący w dół i w prawo. Łuk C F jest ćwiartką okręgu o środku w punkcie S i o ramionach C S oraz F S, każde z ramion ma długość siedem. Prawe końce łuków połączono pionowym odcinkiem E F. Dalsza część drogi biegnie poziomo w prawo i ma kształt prostokąta E F H G, gdzie G H jest końcem drogi i ma długość 4, a krawężniki E G oraz F H są poziome i mają długość 15 każdy.

Pan Kowalski postanowił ją wybetonować, ale by oszacować ilość betonu potrzebną do realizacji tego zadania potrzebuje znać pole powierzchni tej drogi.

Podzielimy całość drogi na fragmenty będące znanymi nam figurami.

Zauważmy, że czworokąty $A B C D$ i $E G H F$ są prostokątami o wymiarach, które możemy odczytać z rysunku.

$P_{A B C D} = |A B| \cdot |A C| = 4 \cdot 5 = 20$

$P_{E G H F} = |E F| \cdot |E G| = 4 \cdot 15 = 60$

Pozostaje nam do obliczenia jedynie fragment $C D E F$ . Zauważmy, że jest on różnicą dwóch wycinków kołowych odpowiadających kątowi $90 °$ .

R1IOso6B7Abl5

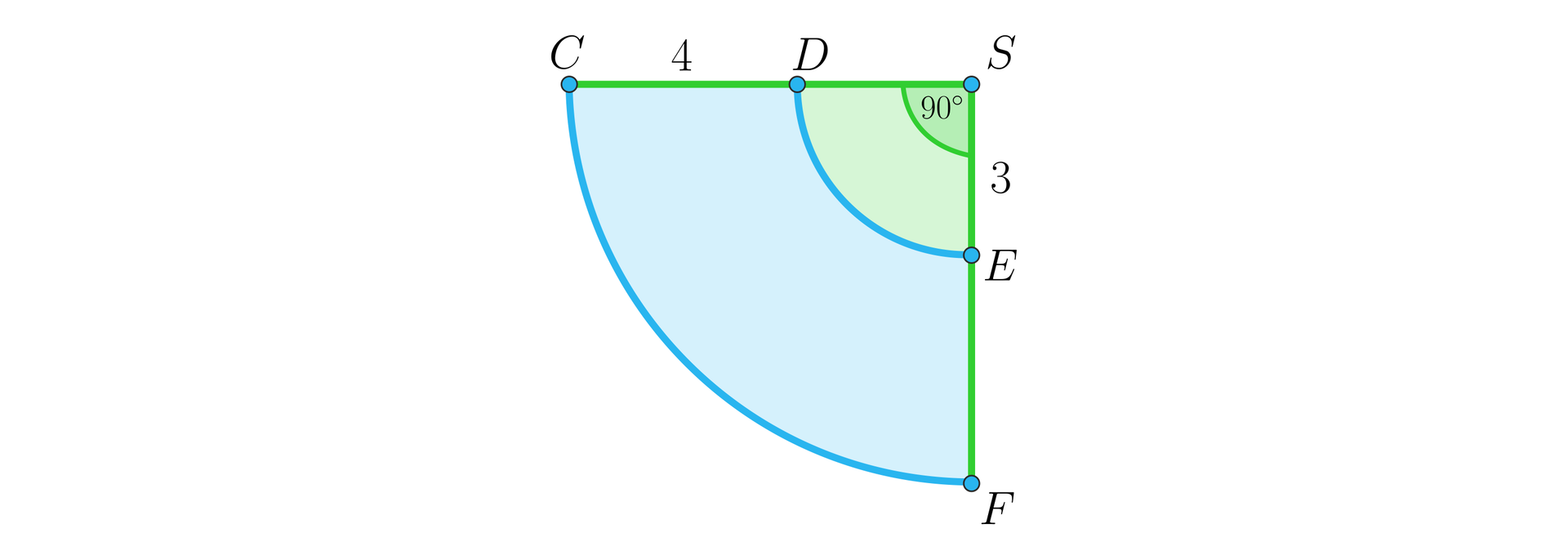
Ilustracja przedstawia dolną lewą ćwiartkę koła o środku w punkcie S. Ćwiartka ograniczona jest jest ramionami S C oraz S F. W tym wycinku wykreślono ćwiartkę mniejszego koła o środku w punkcie S. Mniejsza ćwiartka ograniczona jest ramionami S D pokrywającym się z ramieniem S C oraz ramieniem S E o długości 3, które pokrywa się z ramieniem S F. Przy środku S zaznaczono kąt prosty. Kawałek ramienia dużego koła, czyli odcinek C D ma długość 4, zatem ramię dużego koła ma długość 3 dodać 4 równa się siedem.

Promień mniejszego wycinka, który oznaczymy przez $r$ , ma długość $3$ .

Długość odcinka $C D$ wynosi $4$ , więc promień większego wycinka ma długość $R = 4 + 3 = 7$ .

Zatem powołując się na wzór opisujący pole wycinka koła, możemy obliczyć pole powierzchni drogi ograniczonej przez figurę $C D E F$ (będącą fragmentem pierścienia kołowegopierścień kołowypierścienia kołowego) w sposób następujący:

$P_{C D E F} = \frac{90 °}{360 °} π (7^{2} - 3^{2}) = \frac{90 °}{360 °} π \cdot 40 = \frac{40}{4} π = 10 π$ .

Łączna powierzchnia drogi wynosi więc

$P = P_{A B C D} + P_{C D E F} + P_{E G H F} = 20 + 10 π + 60 = 80 + 10 π$ .

Motyw dzielenia figury na mniejsze fragmenty, usuwania i uzupełniania wybranych fragmentów powierzchni pojawia się w wielu zadaniach, wymagających obliczenia pola powierzchni pewnej niestandardowej figury.

Przyjrzyjmy się kolejnym przykładom.

Przykład 2

W kwadracie $A B C D$ o boku $4$ poprowadzono odcinki łączące środki sąsiadujących boków (oznaczając je literami $E$ , $F$ , $G$ , $H$ ). Następnie narysowano koła o promieniach równych połowie długości boku i wycięto białe fragmenty, zgodnie z rysunkiem poniżej. Oblicz pole pozostałej, zacieniowanej części kwadratu.

R1PgyEWW1OiHY

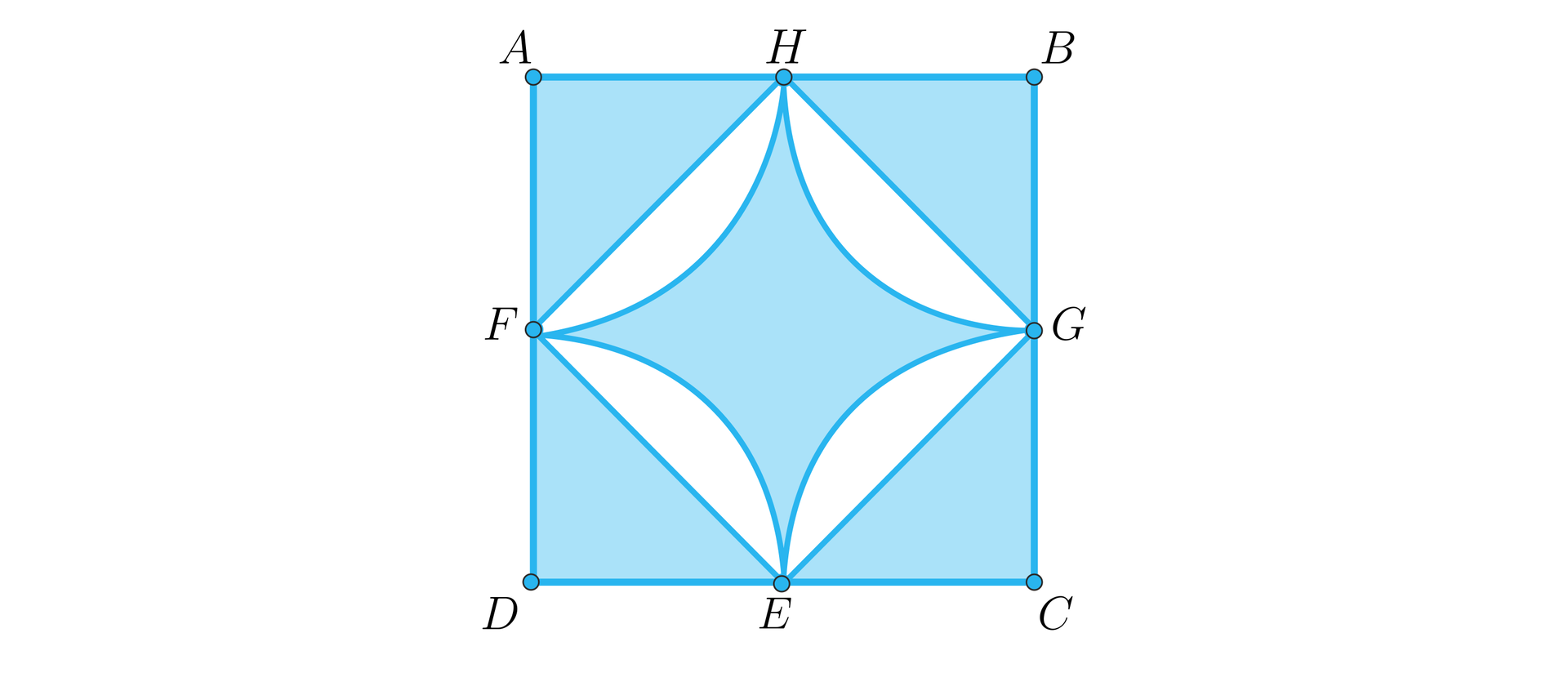
Ilustracja przedstawia kwadrat A B C D. Na środkach boków zaznaczono punkty. Na środku A B oznaczono punkt H, na środku B C oznaczono punkt G, na środku C D oznaczono punkt E, na środku D A oznaczono punkt F. Punkty będące środkami połączono w romb H G E F. Kolorem zaznaczono obszar wewnątrz kwadratu i na zewnątrz rombu. W rombie wykreślono czerty łuki o początkach i końcach w wierzchołkach rombu. Łuki te są wybrzuszone do środka figury. Łuki te to łuk H G, łuk G E, łuk E F oraz łuk F H. Zaznaczono tym samym kolorem obszar między łukami.

Pole całego kwadratu $A B C D$ wynosi $P_{A B C D} = 4^{2} = 16$ . Od tej wartości musimy odjąć pole powierzchni niezacieniowanej – oznaczmy je przez $P *$ .

Jak obliczyć wartość $P *$ ? Przypatrzmy się pojedynczej ćwiartce tego kwadratu.

R6YnXDZwi3EOd

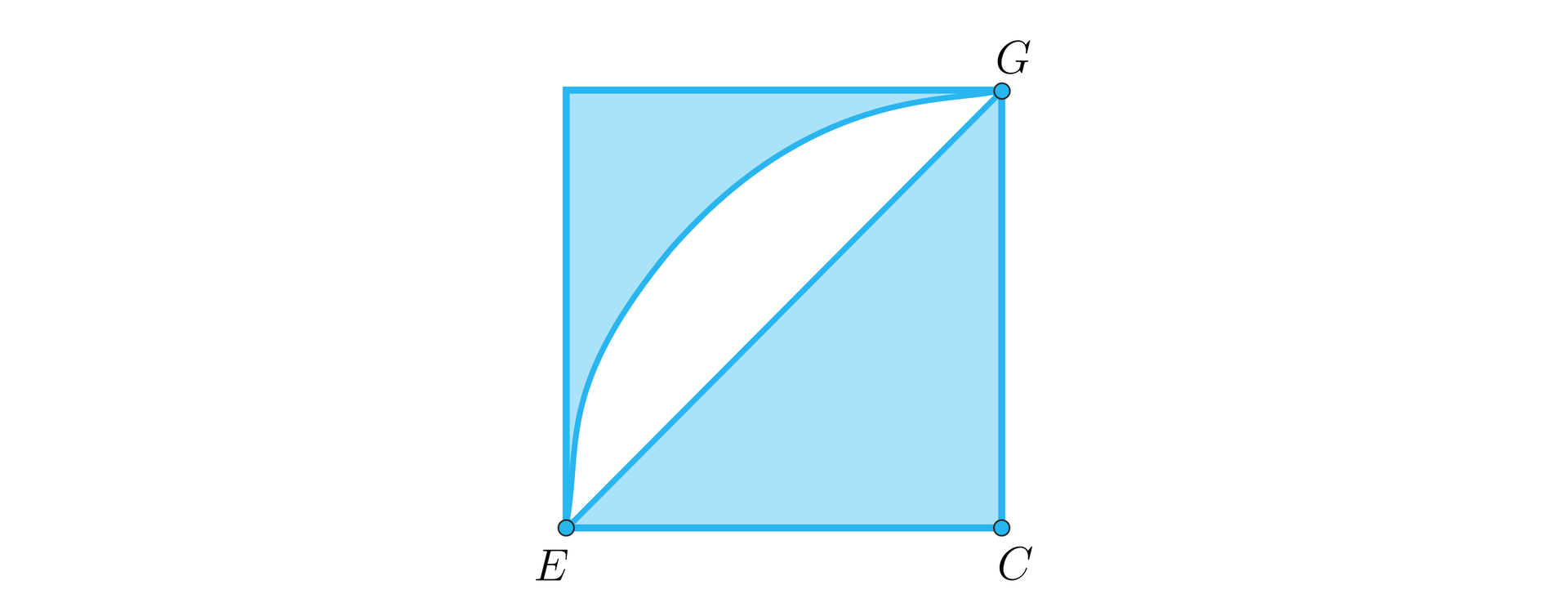
Ilustracja przedstawia kwadrat. Oznaczono tylko trzy wierzchołki: prawy górny G, dolny prawy C lewy dolny to W. W kwadracie wykreślono przekątną E G, na której oparty jest łuk wybrzuszony w stronę nieoznaczonego górnego lewego wierzchołka. Kolorem zaznaczono wnętrze figury poza obszarem znajdującym się między łukiem a przekątną.

Pole białego fragmentu z pojedynczej ćwiartki możemy wyliczyć, odejmując od pola wycinka koła (odpowiadającemu kątowi prostemu) pole trójkąta rozpiętego na wierzchołku kwadratu i środkach sąsiadujących z tym wierzchołkiem boków. Dla omawianej, prawej dolnej ćwiartki będzie to pole trójkąta $E C G$ . Jest to trójkąt prostokątny równoramienny – długość jego ramienia jest równa połowie boku kwadratu, czyli $2$ . Zatem:

$P_{△} = \frac{1}{2} \cdot 2 \cdot 2 = 2$ .

Z kolei omawiany wycinek koła ma pole

$P_{w} = \frac{90 °}{360 °} \cdot π \cdot 2^{2} = \frac{1}{4} \cdot 4 π = π$ .

Zatem biała powierzchnia, której pole musimy odjąć od pola powierzchni całego kwadratu stanowi czterokrotność różnicy $P_{w}$ i $P_{△}$ .

$P * = 4 \cdot (P_{w} - P_{△}) = 4 \cdot (π - 2) = 4 π - 8$ .

Ostatecznie pole zacieniowanego obszaru wynosi

$P = P_{A B C D} - P * = 16 - (4 π - 8) = 16 - 4 π + 8 = 24 - 4 π$ .

Przykład 3

Trójkąt $A B C$ jest trójkątem równobocznym, a długość jego boku wynosi $18$ . Długości odcinków łączących punkty $F$ i $E$ oraz $E$ i $D$ wynoszą odpowiednio $2$ i $6$ . Oblicz pole zacieniowanego obszaru wiedząc, że punkty $C, F, E, D$ są współliniowe.

R17zfQcGehAkD

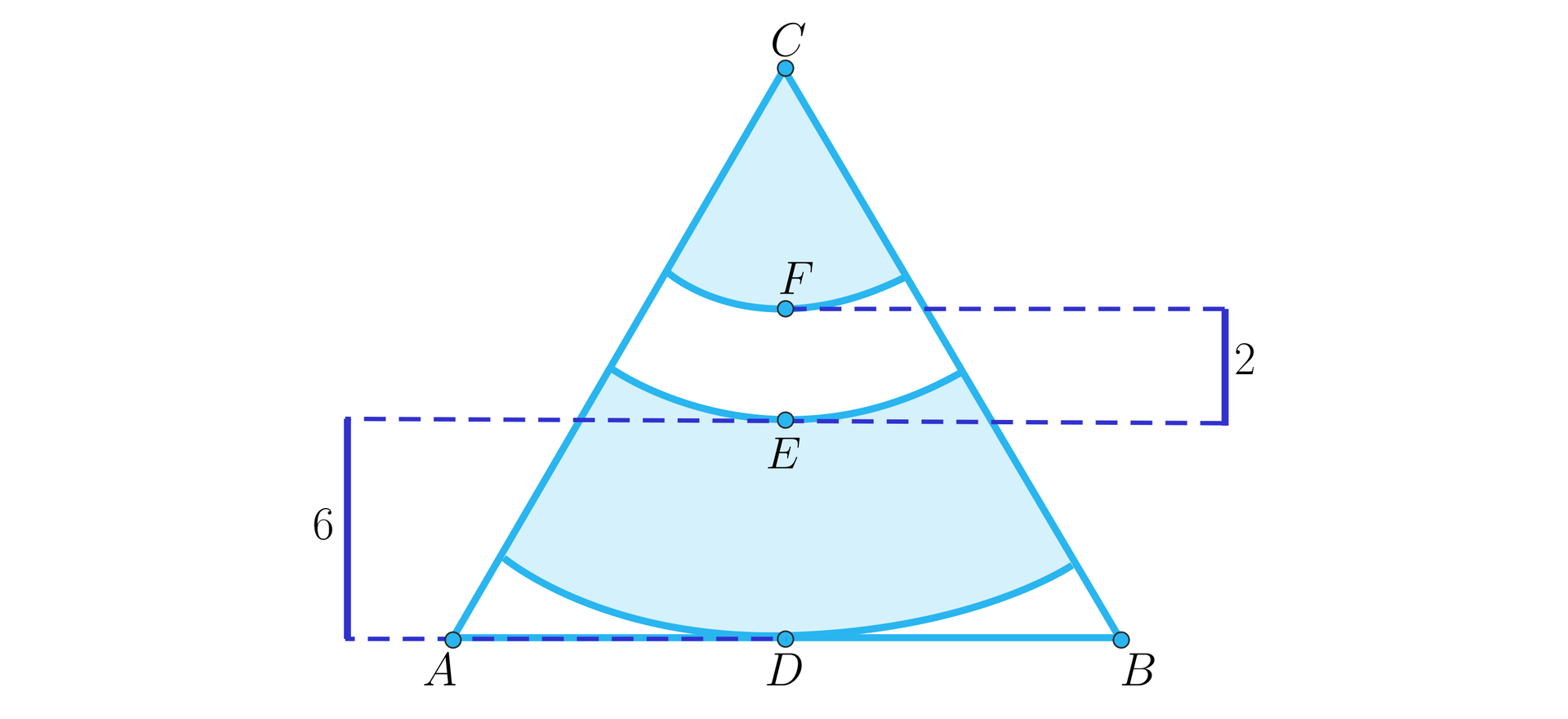
Ilustracja przedstawia trójkąt równoboczny A B C, gdzie C to górny wierzchołek pokrywający się ze środkiem koła. Na trójkąt naniesiono kilka wycinków kół o środku w punkcie C, ale o różnych promieniach. Promienie wycinków pokrywają się z ramionami A C oraz B C. Pod wierzchołkiem C na brzegach kolejnych kół oznaczono punkty kolejno: F, E, D. Kolorem zaznaczono wycinek koła od D do F, wycinek pierścienia o szerokość F E równej dwa jest bez tła, następnie kolorem zaznaczono wycinek pierścienia między punktami E i D, przy czym D znajduje się na środku podstawy A B trójkąta. Szerokość pierścienia E D wynosi sześć.

Z faktu, iż $A B C$ jest trójkątem równobocznym wnioskujemy, że kąt $∢ A C B$ ma miarę $60 °$ , zaś odcinek łączący punkty $C$ i $D$ jest wysokością całego rozważanego trójkąta. Niezależnie od argumentacji, jesteśmy w stanie wyliczyć długość $|C D|$ :

$|C D| = \frac{18 \sqrt{3}}{2} = 9 \sqrt{3}$ .

Możemy zatem wyliczyć kolejno długości odcinków $C F$ i $C E$ :

$|C F| = |C D| - (|D E| + |E F|) = 9 \sqrt{3} - (2 + 6) = 9 \sqrt{3} - 8$ ,

$|C E| = |C D| - |D E| = 9 \sqrt{3} - 6$ .

Możemy zauważyć, że obliczenie pola zacieniowanej powierzchni sprowadza się do trzech zasadniczych kroków:

a) Wyliczenie pola powierzchni wycinka kołowego, w którym promieniem jest odcinek $C D$ , zaś kątem środkowym jest kąt $∢ A C B$ . Z uwagi na to, że $A B C$ jest trójkątem równobocznym, wiemy że $∢ A C B = 60 °$ .

Pole to oznaczymy przez $P_{C D}$ . Zatem

$P_{C D} = \frac{60 °}{360 °} \cdot π \cdot {(9 \sqrt{3})}^{2} = \frac{1}{6} \cdot 81 \cdot 3 π = \frac{81 π}{2}$ .

b) Od $P_{C D}$ odejmujemy pole powierzchni wycinka opartego na tym samym kącie środkowym $∢ A C B$ , ale o promieniu $C E$ , które oznaczymy przez $P_{C E}$ . Korzystając ze wzorów skróconego mnożenia otrzymujemy

$P_{C E} = \frac{60 °}{360 °} \cdot π \cdot {(9 \sqrt{3} - 6)}^{2} = \frac{π}{6} \cdot (81 \cdot 3 - 2 \cdot 6 \cdot 9 \sqrt{3} + 36) =$

$= \frac{π}{6} \cdot (279 - 108 \sqrt{3}) = \frac{93 π}{2} - 18 \sqrt{3} π$ .

Zatem $P_{C D} - P_{C E} = \frac{81 π}{2} - (\frac{93 π}{2} - 18 \sqrt{3} π) = \frac{- 12 π}{2} + 18 \sqrt{3} π = (18 \sqrt{3} - 6) π$ .

c) Ostateczny wynik uzyskamy dodając do rezultatu poprzednich obliczeń $P_{C F}$ , czyli pole powierzchni wycinka koła o tym samym kącie środkowym i promieniu $C F$ .

$P_{C F} = \frac{60 °}{360 °} \cdot π \cdot {(9 \sqrt{3} - 8)}^{2} = \frac{π}{6} \cdot (81 \cdot 3 - 2 \cdot 8 \cdot 9 \sqrt{3} + 64) =$

$= \frac{π}{6} \cdot (307 - 144 \sqrt{3}) = \frac{307 π}{6} - 24 \sqrt{3} π$ .

Ostatecznie pole całej zacieniowanej powierzchni wynosi

$P = (P_{C D} - P_{C E}) + P_{C F} = (18 \sqrt{3} - 6) π + \frac{307 π}{6} - 24 \sqrt{3} π =$

$= (51 \frac{1}{6} - 6) π + (18 - 24) \sqrt{3} π = (45 \frac{1}{6} - 6 \sqrt{3}) π$ .

W kolejnym przykładzie rozważymy przecięcie dwóch nachodzących na siebie kół.

Przykład 4

Dwa okręgi o promieniach $3 \sqrt{3}$ nałożono na siebie w taki sposób, że odległość odcinka $|A B|$ łączącego punkty przecięcia tych okręgów jest równa długości promienia każdego z nich. Jakie pole powierzchni ma obszar znajdujący się we wnętrzu obydwu tych okręgów jednocześnie?

Zobrazujmy tę sytuację – naszym zadaniem jest obliczenie pola powierzchni zacieniowanego obszaru. Punkty $O_{1}$ , $O_{2}$ stanowią środki rozważanych w zadaniu okręgów.

R1SXKKWVnbkit

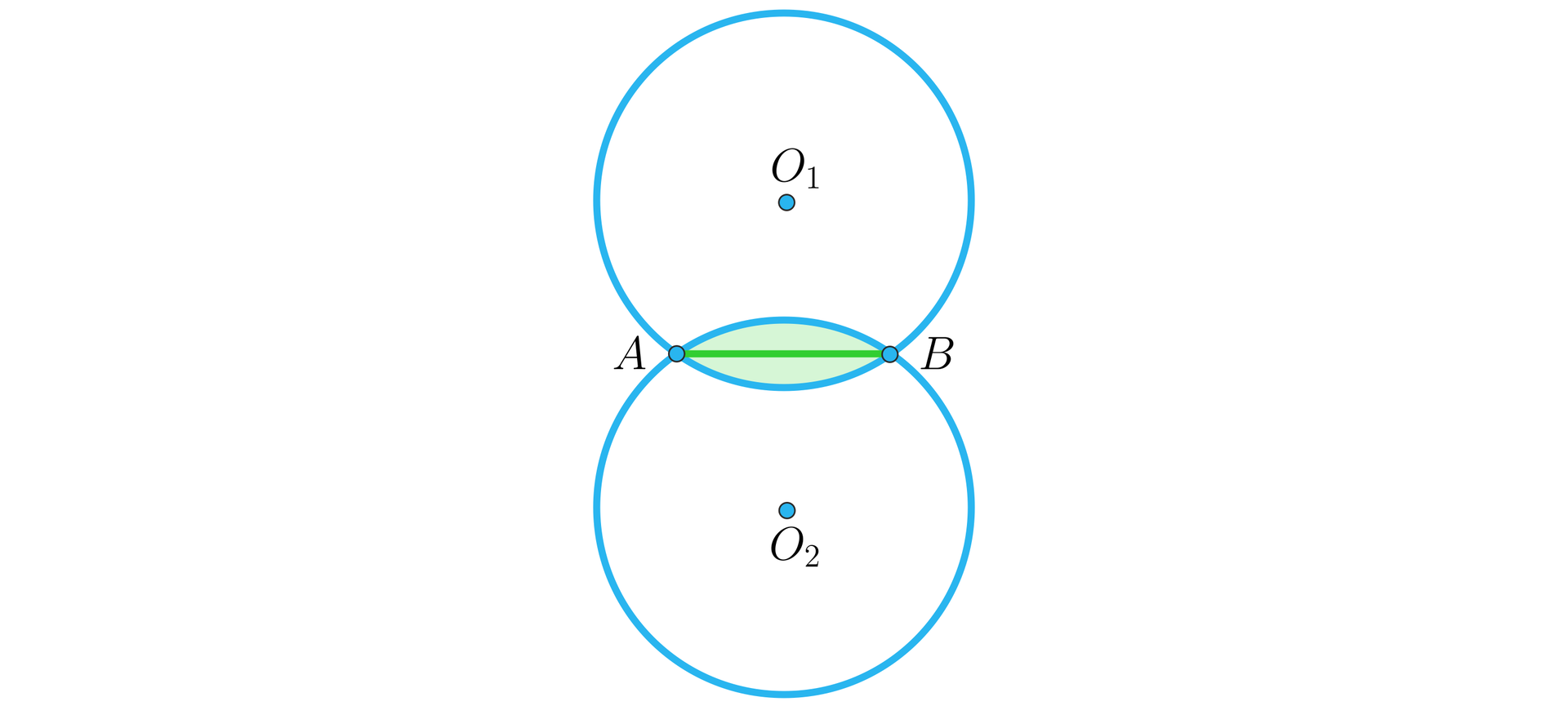
Ilustracja przedstawia równe dwa okręgi przecinające się. Górny okrąg ma środek w punkcie O indeks dolny 1 koniec indeksu, okrąg pod nim ma środek w punkcie O indeks dolny 2 koniec indeksu. Okręgi przecinają się w punktach A oraz B, obszar przecięcia zaznaczono kolorem oraz poprowadzono odcinek A B.

Z treści zadania wynika, że odległość dzieląca punkty $A$ i $B$ jest równa promieniowi każdego z rozpatrywanych okręgów. Zatem punkty $O_{1}$ , $A$ , $B$ tworzą trójkąt równoboczny o boku $a = 3 \sqrt{3}$ – podobnie jak punkty $O_{2}$ , $A$ , $B$ . Szukane pole zacieniowanego obszaru stanowi zatem część wspólną dwóch wycinków kół, odpowiadających kątom $60 °$ – bo taką właśnie miarę mają wszystkie kąty w rozważanych przez nas trójkątach.

R1OC0UjPrOEHb

Pole to możemy wyliczyć, obliczając pole powierzchni każdego z tych wycinków i odejmując od niego pole stosownego trójkąta równobocznego – $A B O_{1}$ lub $A B O_{2}$ , a następnie sumując uzyskane wyniki. Oczywiście pola obydwu tych wycinków (podobnie jak pola tych trójkątów) są takie same.

Wycinek oparty na kącie $∢ A O_{1} B$ ma pole

$P_{∢ A O_{1} B} = \frac{60 °}{360 °} \cdot π \cdot {(3 \sqrt{3})}^{2} = \frac{1}{6} \cdot π \cdot 27 = \frac{9 π}{2}$ .

Pamiętając, że pole trójkąta równobocznego wyraża się wzorem

$P_{△} = \frac{a^{2} \sqrt{3}}{4}$ ,

(gdzie $a$ jest długością boku tego trójkąta) mamy

$P_{△ A B O_{1}} = \frac{{(3 \sqrt{3})}^{2} \cdot \sqrt{3}}{4} = \frac{27 \sqrt{3}}{4}$ .

Możemy zatem obliczyć już pole dolnej połowy zacieniowanego obszaru – wynosi ono

$P_{◡}$ $= P_{∢ A O_{1} B} - P_{△ A B O_{1}} = \frac{9 π}{2} - \frac{27 \sqrt{3}}{4} = \frac{18 π - 27 \sqrt{3}}{4}$ .

Mając na uwadze to, że (dzięki symetrii) całość szukanej powierzchni stanowi dwukrotność pola obliczonego powyżej $P_{◡}$ możemy stwierdzić, że

$P = 2 P_{◡}$ $= \frac{18 π - 27 \sqrt{3}}{2}$

jest polem całości zacieniowanego obszaru.

Słownik

kąt środkowy

kąt, którego wierzchołkiem jest środek tego okręgu, a ramionami są półproste zawierające promienie tego okręgu

kąt pełny

kąt o mierze równej $360 °$

łuk okręgu

część okręgu wyznaczona przez ramiona kąta środkowego tego okręgu

pierścień kołowy

podzbiór płaszczyzny ograniczony dwoma okręgami o wspólnym środku i różnych promieniach

Wprowadzenie

Aplet

Słownik