Przeczytaj

Już wiesz

Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej naprzeciw tego kąta do długości przeciwprostokątnej.

Cosinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej przy kącie do długości przeciwprostokątnej.

Tangensem kąta ostrego w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej leżącej naprzeciw tego kąta do długości drugiej przyprostokątnej.

Przykład 1

Dany jest trójkąt prostokątny $A B C$ o przeciwprostokątnej $A B$ , w którym tangens kąta $A B C$ jest równy $\frac{24}{7}$ i $|A C| = 9, 6$ . Obliczymy pole koła opisanego na tym trójkącie.

Rozwiązanie

RgnvB59w1fjOs1

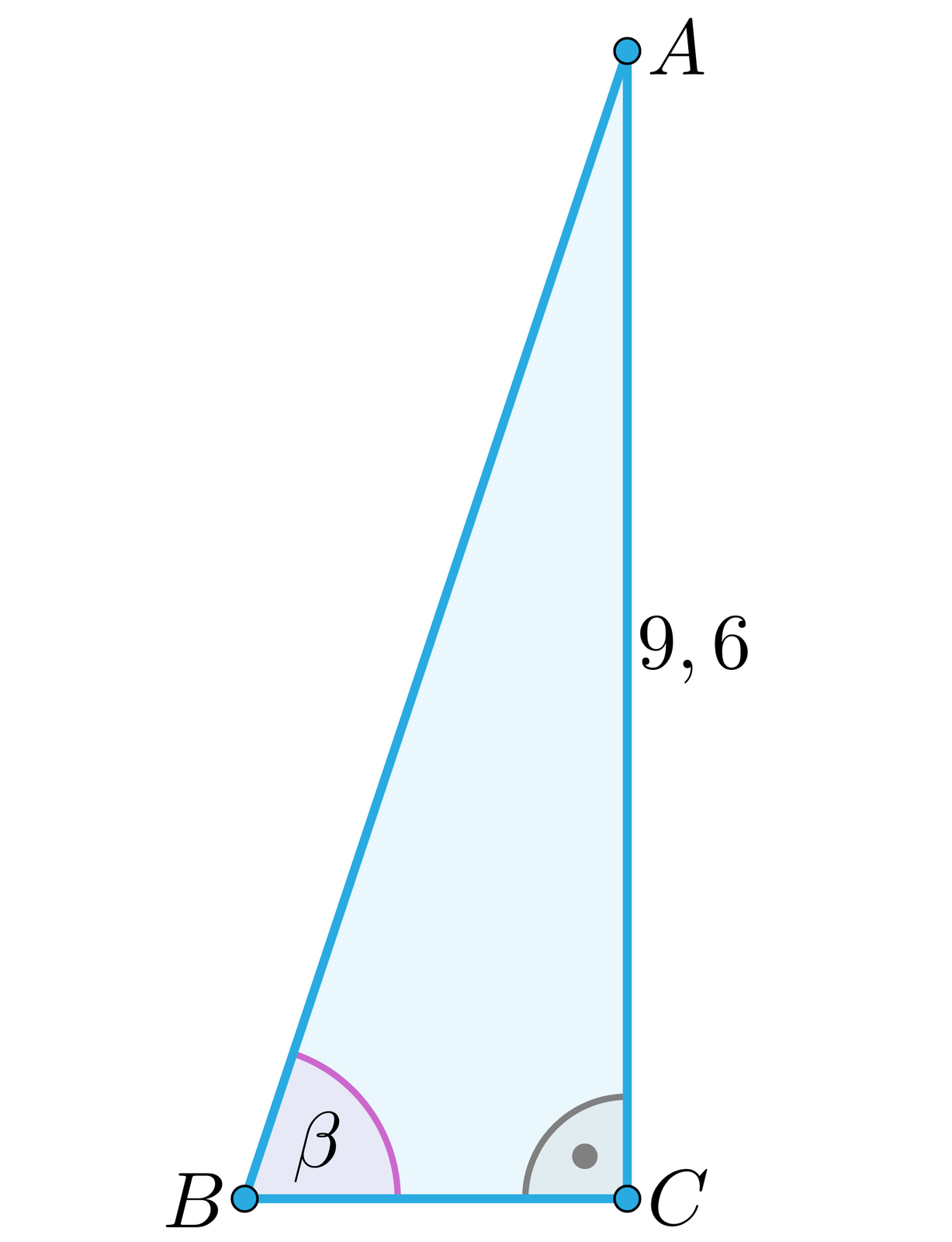
Ilustracja przedstawia trójkąt prostokątny A B C taki, że przyprostokątnymi są boki B C oraz C A , CA=9,6 oraz <math∢ABC=β.

Tangens kąta $A B C$ to iloraz $\frac{|A C|}{|B C|}$ ,

czyli: $\frac{9, 6}{|B C|} = \frac{24}{7}$ ,

$|B C| = 2, 8$

Z twierdzenia Pitagorasa: ${|B C|}^{2} + {|A C|}^{2} = {|A B|}^{2}$

a zatem:

$|A B| = \sqrt{{(2, 8)}^{2} + {(9, 6)}^{2}} = \sqrt{100} = 10$ .

Ponieważ $A B$ jest średnicą koła opisanego na trójkącie $A B C$ , więc promień tego koła jest równy $5$ , a pole koła wynosi $π \cdot 5^{2} = 25 π$ .

Przykład 2

Obliczymy pole i obwód trapezu równoramiennego, w którym podstawy mają długości $6$ i $10$ , a ramię tworzy z dłuższą podstawą kąt $60^{\circ}$ . Ustalimy też, jaka jest wartość tangensa kąta nachylenia przekątnej tego trapezu do jego dłuższej podstawy.

Rozwiązanie

Przyjmijmy oznaczenia, jak na rysunku.

RRyPHU3A6Np6p

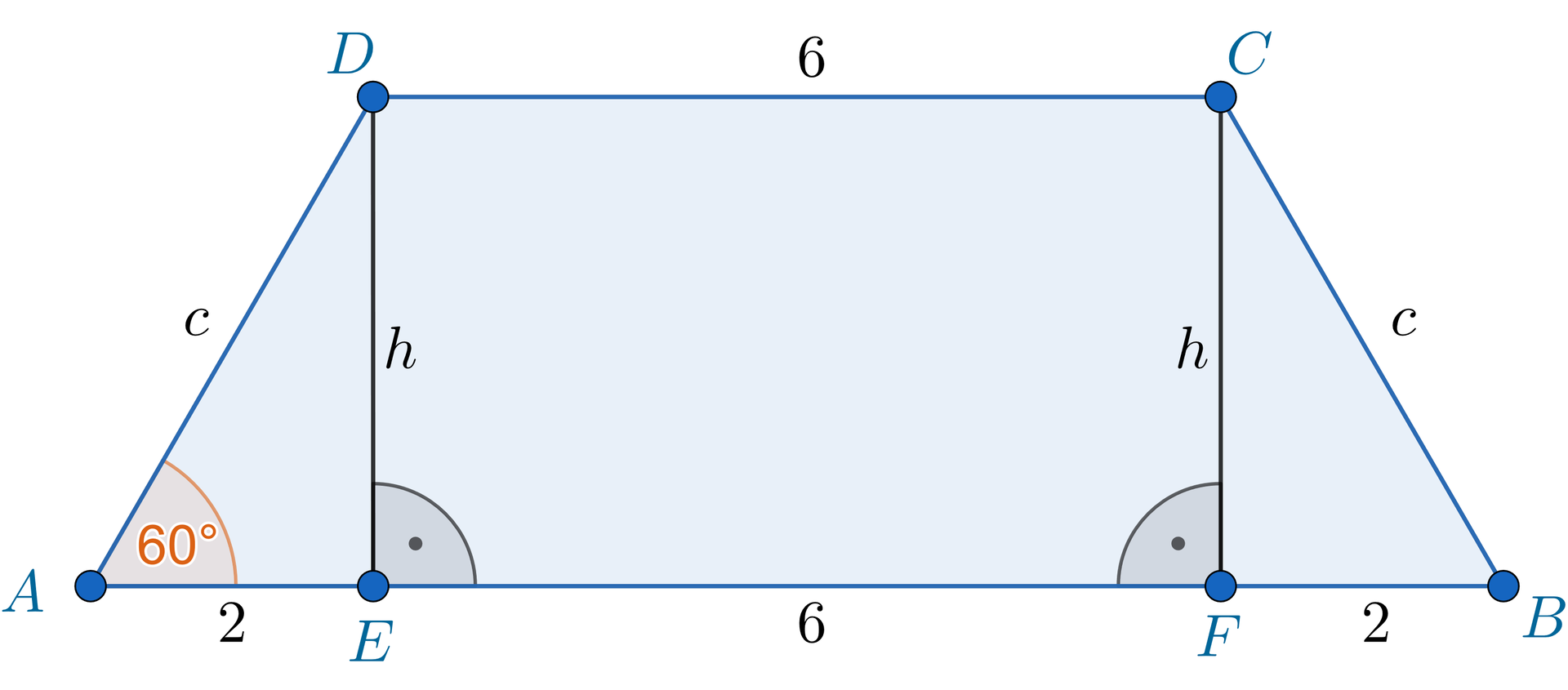
Ilustracja przedstawia trapez równoramienny A B C D. Górna podstawa C D ma długość sześć. Z wierzchołka D poprowadzono wysokość na dolną podstawę i spodek wysokości oznaczono jako punkt E. Wówczas odcinek A E ma długość 2 oraz kąt przy wierzchołku A ma miarę sześćdziesiąt stopni. Z wierzchołka C również poprowadzono wysokość na dolną podstawę tak, że spodek wysokości oznaczono jako punkt F. Odcinek F B ma długość 2. Odcinek E F ma długość sześć. Ramiona trapezu mają długość c.

Wysokości $C F$ i $D E$ dzielą trapez na prostokąt i dwa przystające trójkątytrójkąty przystająceprzystające trójkąty prostokątne, w których jedna z przyprostokątnych ma długość $2$ , a przyległy do niej kąt ostry ma miarę $60^{\circ}$ .

Ważne!

Można też od razu zauważyć, że po sklejeniu trójkątów $A D E$ i $B C F$ wzdłuż dłuższej przyprostokątnej otrzymujemy trójkąt równobocznytrójkąt równobocznytrójkąt równoboczny.

Wobec tego:

$\frac{h}{2} = tg 60^{\circ} = \sqrt{3}$ ,

stąd $h = 2 \sqrt{3}$ , a także $\frac{2}{c} = \cos 60^{\circ} = \frac{1}{2}$ , czyli $c = 4$ .

Pole trapezu jest zatem równe:

$\frac{1}{2} (10 + 6) \cdot 2 \sqrt{3} = 16 \sqrt{3}$ ,

a obwód wynosi $24$ .

Oznaczmy z kolei przez $α$ kąt nachylenia przekątnej $A C$ do podstawy $A B$ .

R183PCxkCfpLY

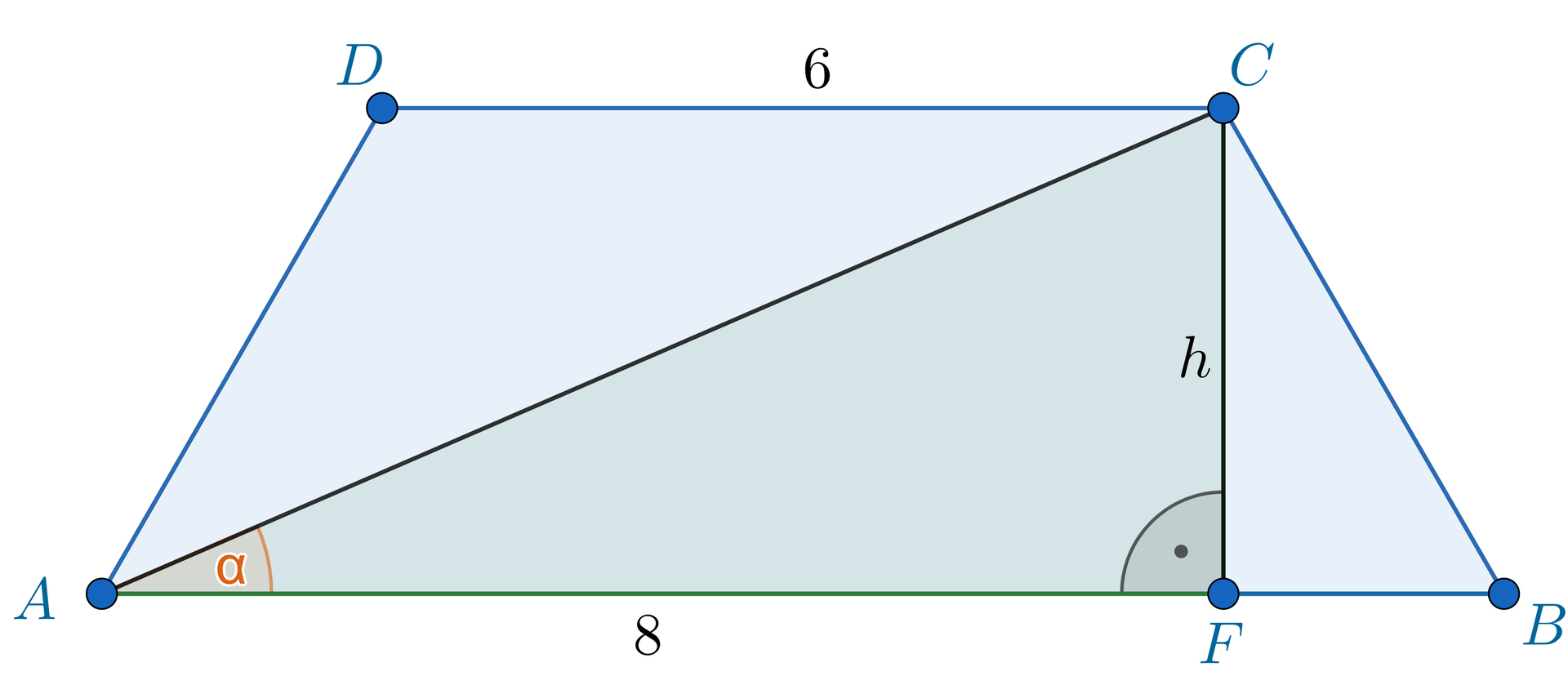
Ilustracja przedstawia trapez A B C D. Górna podstawa C D ma długość sześć. Z wierzchołka C poprowadzono wysokość na dolną podstawę i jej spodek oznaczono jako punkt F. Odcinek A F ma długość osiem. W trapezie poprowadzono również przekątną A C ,która jest nachylona do dolnej podstawy pod kątem alfa.

W trójkącie prostokątnym $A F C$ mamy: $tg α = \frac{2 \sqrt{3}}{8} = \frac{\sqrt{3}}{4}$ .

Przykład 3

W trójkącie $A B C$ dane są $|A B| = 8$ , $|A C| = 6$ i $|∢ C A B| = 30^{\circ}$ . Obliczymy pole tego trójkąta.

Rozwiązanie

Poprowadźmy wysokość $C D$ z wierzchołka $C$ na bok $A B$ , jak na rysunku.

R151toFlcGYcl

Ilustracja przedstawia trójkąt A B C. Z wierzchołka C poprowadzono wysokość na podstawę A B i jej spodek wysokości oznaczono przez punkt D. Miara kąta przy wierzchołku A wynosi trzydzieści stopni.

W trójkącie prostokątnym $A D C$ mamy:

$|A C| = 6$ oraz $|∢ C A D| = |∢ C A B| = 30^{\circ}$ .

Zgodnie z definicją sinusa:

$\frac{|C D|}{|A C|} = \sin 30^{\circ} = \frac{1}{2}$

$|C D| = \frac{1}{2} |A C| = 3$

i w konsekwencji pole trójkąta $A B C$ jest równe $\frac{1}{2} \cdot 8 \cdot 3 = 12$ .

o polu trójkąta

Twierdzenie: o polu trójkąta

Pole trójkąta o bokach $a$ oraz $b$ i kącie ostrym $α$ zawartym pomiędzy nimi jest równe:

$P = \frac{1}{2} a b \sin α$ .

Dowód

R12TkEKYn4YmG

Ilustracja przedstawia trójkat A B C. Z wierzchołka C poprowadzono wysokość na podsatwę A B i jej spodek wysokości oznaczono przez punkt D. Miara kąta przy wierzchołku A wynosi trzydzieści stopni. Bok A C ma długość a, odcinek A D ma długość b, wysokość C D ma długość a razy sinus kąta alfa.

Niech w trójkącie $A B C$ kąt przy wierzchołku $α$ będzie ostry i niech $|A B| = b$ oraz $|A C| = c$ .

Opuśćmy na bok $A B$ wysokość z wierzchołka $C$ .

Wówczas wysokość $C D$ jest równa:

$|C D| = |A C| \cdot \sin ∢ B A C = a \sin α$ .

Zatem pole trójkąta $A B C$ jest równe:

$P = \frac{1}{2} a b \sin α$ .

Przykład 4

Obliczymy przybliżoną wartość pola trójkąta o bokach $a = 4$ , $b = 7$ oraz kącie $α = 17^{\circ}$ , zawartym między tymi bokami, podając wynik w zaokrągleniu do części setnych.

Rozwiązanie

Mamy:

$P = \frac{1}{2} \cdot 4 \cdot 7 \cdot \sin 17^{\circ} = 14 \sin 17^{\circ} \approx 4, 09$ .

Przykład 5

Obliczymy pole równoległoboku, w którym przekątne o długościach $4$ i $10$ przecinają się pod kątem $45^{\circ}$ .

Rozwiązanie

RRNG40XgWgDVR

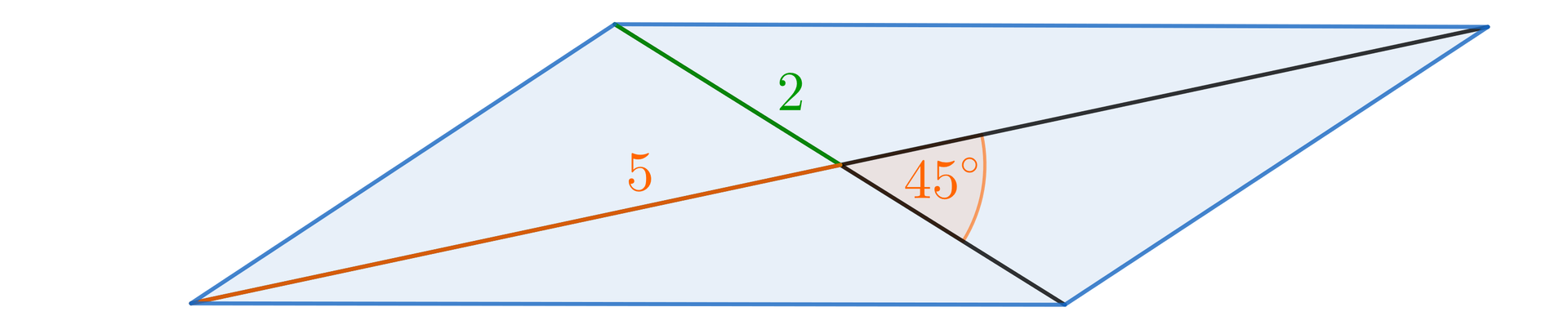
Ilustracja przedstawia równoległobok z poprowadzonymi przekątnymi. Połowa krótszej przekątnej ma długość dwa, a poła dłuższej przekątnej ma długość 5. Przekątne przecinają się pod kątem czterdziestu pięciu stopni.

Zauważmy najpierw, że przekątne dzielą równoległobok na cztery trójkąty o równych polach (wynika to stąd, że jedna przekątna dzieli równoległobok na dwa trójkąty przystające, a druga przekątna dzieli powstałe trójkąty wzdłuż środkowej). W każdym z tych czterech trójkątów możemy wyróżnić dwa boki o długościach odpowiednio $2$ i $5$ , a w dwóch z nich kąt między tymi odcinkami jest równy $45^{\circ}$ .

Stąd pole równoległoboku jest równe:

$P = 4 \cdot \frac{1}{2} \cdot 2 \cdot 5 \cdot \sin 45^{\circ} = 10 \sqrt{2}$ .

Pole równoległoboku jest równe $10 \sqrt{2}$ .

Przykład 6

Obliczymy długości przekątnych równoległoboku $A B C D$ , którego kąt ostry przy wierzchołku $A$ ma miarę $60^{\circ}$ , a boki $A D$ i $A B$ mają długości odpowiednio $6$ i $16$ .

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku.

RaKGKQOcZsyOP

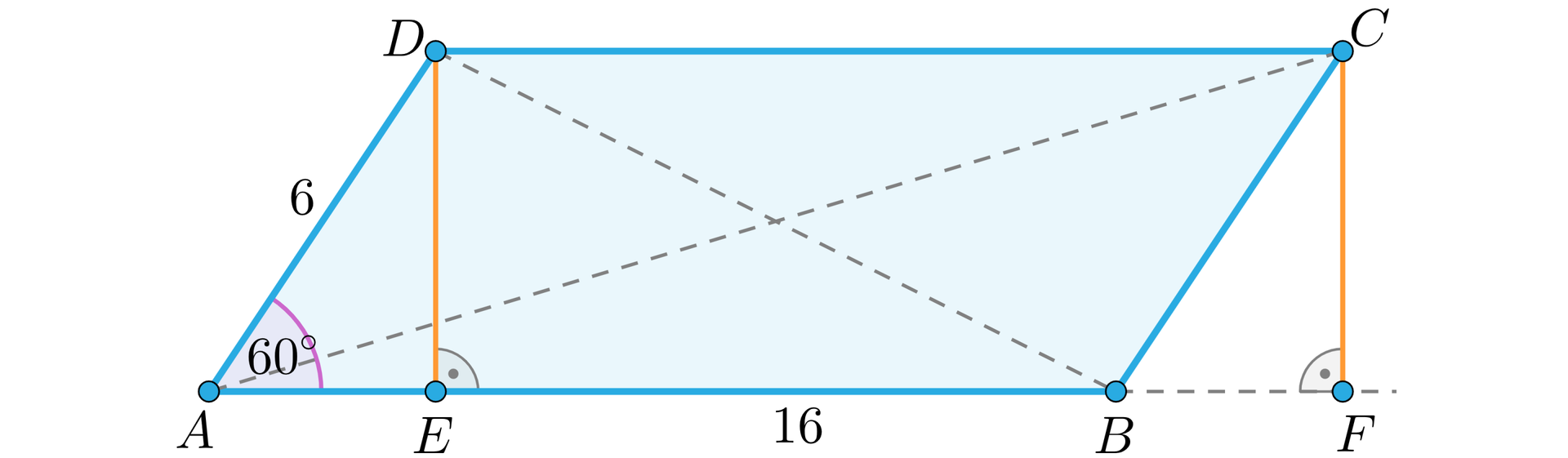
Ilustracja przedstawia równoległobok A B C D z poprowadzonymi za pomocą przerywanej linii przekątnymi A C oraz B D . Bok A B ma długość 16, a A D 6. Z wierzchołka D poprowadzono wysokość na bok A B i spodek wysokości oznaczono jako punkt E. W wierzchołka C poprowadzono wysokość na przedłużenie boku A B. Spodek tej wysokości oznaczono przez punk F. Kąt przy wierzchołku A ma miarę sześćdziesięciu stopni.

W trójkącie prostokątnym $A D E$ :

$\frac{|D E|}{|A D|} = \sin 60^{\circ} = \frac{\sqrt{3}}{2}, \frac{|A E|}{|A D|} = \cos 60^{\circ} = \frac{1}{2}$

stąd:

$|D E| = 3 \sqrt{3}, |A E| = 3$ .

Wobec tego:

$|B E| = 16 - 3 = 13$ i $|A F| = 16 + 3 = 19$ .

Korzystając z twierdzenia Pitagorasa w trójkątach $D E B$ i $A F C$ , mamy:

$|B D| = \sqrt{{(3 \sqrt{3})}^{2} + 13^{2}} = \sqrt{27 + 169} = \sqrt{196} = 14$ , $|A C| = \sqrt{{(3 \sqrt{3})}^{2} + 19^{2}} = \sqrt{27 + 361} = \sqrt{388} = 2 \sqrt{97}$ .

Przekątne tego równoległoboku mają długości $14$ oraz $2 \sqrt{97}$ .

Słownik

trójkąt równoboczny

trójkąt, którego wszystkie boki mają taką samą długość, szczególny przypadek trójkąta równoramiennego

trójkąty przystające

trójkąty, w których odpowiednie boki są równe i odpowiednie kąty mają równe miary

Wprowadzenie

Animacja

Słownik