Przeczytaj

Przypomnijmy definicję okręgu opisanego na trójkącie.

Okrąg opisany na trójkącie

Definicja: Okrąg opisany na trójkącie

Mówimy, że okrąg jest opisany na trójkącie wtedy, gdy wszystkie wierzchołki tego trójkąta należą do okręgu.

Rw1OSYF4mYd1A

Ilustracja przedstawia trójkąt wpisany w okrąg. Każdy wierzchołek trójkąta styka się z okręgiem. Zaznaczono promień R wychodzący z wierzchołku trójkąta.

Przez $R$ oznaczmy promień okręgu opisanego na trójkącie.

Okrąg można opisać na każdym trójkacie. I odwrotnie - każdy trójkąt można wpisać w okrąg.

Środek okręgu opisanego na trójkącie jest punktem przecięcia symetralnych boków trójkąta.

Wyznaczymy wzór na pole trójkąta, w zależności od rodzaju trójkąta, przy użyciu długości promienia okręgu opisanego na tym trójkącie.

Pole trójkąta równobocznego, na którym opisano okrąg o promieniu $R$

RAKKu38xlsKLr

Ilustracja przedstawia trójkąt równoboczny o boku wpisany w okręg o promieniu R. Zaznaczono dwie wysokości trójkąta.

Przyjmijmy oznaczenia takie, jak na rysunku. Symetralne boków trójkąta zawierają wysokości, a wysokości i środkowe trójkąta przecinają się w jednym punkcie, będącym środkiem okręgu opisanego na tym trójkącie i dzielą się w stosunku $2 : 1$ . Stąd

R = \frac{2}{3} h

oraz

h = \frac{a \sqrt{3}}{2}

Zatem

R = \frac{a \sqrt{3}}{3}

, więc

a = R \sqrt{3}

Wobec tego pole trójkąta równobocznego wyraża się wzorem

P = \frac{a^{2} \sqrt{3}}{4} = \frac{{(\sqrt{3} R)}^{2} \cdot \sqrt{3}}{4} = \frac{3 \sqrt{3} R^{2}}{4}

Przeciwprostokątna trójkąta prostokątnego, na którym opisano okrąg o promieniu $R$

Środek okręgu opisanego na trójkącie prostokątnym jest punktem będącym środkiem jego przeciwprostokątnej.

R1Gw6gJLOFeHK

P = \frac{1}{2} \cdot a \cdot b

oraz

R = \frac{c}{2}

Zatem

c = 2 R

oraz

a^{2} + b^{2} = {(2 R)}^{2} = 4 R^{2}

Pole dowolnego trójkąta, na którym opisano okrąg o promieniu $R$

RWyoeVNU3gLll

Ilustracja przedstawia trójkąt wpisany w okrąg o kątach wewnętrznych równych alfa, beta oraz gamma oraz długościach boków a b c. Zaznaczono trzy promienie R okręgu wychodzące z wierzchołków trójkąta.

Pole trójkąta obliczamy ze wzoru:

P = \frac{1}{2} \cdot a \cdot b \cdot \sin γ

Z twierdzenia sinusówtwierdzenie sinusówtwierdzenia sinusów zachodzą następujące zależności:

\frac{a}{\sin α} = 2 R

, zatem

a = 2 R \sin α

\frac{b}{\sin β} = 2 R

, zatem

b = 2 R \sin β

\frac{c}{\sin γ} = 2 R

, zatem

c = 2 R \sin γ

Wobec tego

P = \frac{1}{2} a b \cdot \frac{c}{2 R} = \frac{a b c}{4 R}

P = \frac{1}{2} \cdot a \cdot b \cdot \sin γ = \frac{1}{2} \cdot 2 R \sin α \cdot 2 R \sin β \cdot \sin γ = 2 R^{2} \sin α \sin β \sin γ

Otrzymane wzory na pole trójkąta, w zależności od długości promienia okregu opisanego na tym trójkącie, są używane do rozwiązywania bardziej złożonych problemów matematycznych.

W obliczeniach czasami będziemy używać wzoru Herona, za pomocą którego obliczamy pole dowolnego trójkąta, gdy dane są długości trzech jego boków.

P = \sqrt{p \cdot (p - a) \cdot (p - b) \cdot (p - c)}

, gdzie

a, b, c

są długościami boków trójkąta oraz

p = \frac{a + b + c}{2}

Jeżeli użyjemy wyżej wyprowadzonych zależności, to:

p = \frac{2 R \sin α + 2 R \sin β + 2 R \sin γ}{2} = R (\sin α + \sin β + \sin γ)

Przykład 1

Obliczymy pole trójkąta prostokątnego, w którym jedna przyprostokątna ma długość $4$ , a promień okręgu opisanego na tym trójkącie wynosi $6$ .

Rozwiązanie:

Narysujmy trójkąt oraz opisany na nim okrąg i wprowadźmy oznaczenia, jak na rysunku.

REuOMxo1GQGjD

Ilustracja przedstawia trójkąt prostokątny o przyprostokątnych a i 4 oraz przeciwprostokątnej c wpisany w okrąg o promieniu sześć. Przeciwprostokątna to dwa promienie okręgu.

Niech $R$ będzie długością promienia okręgu opisanego na tym trójkącie. Zatem

$c = 2 R = 2 \cdot 6 = 12$

Zatem do wyznaczenia wartości $a$ rozwiązujemy równanie, utworzone na podstawie twierdzenia Pitagorasa:

$a^{2} + 4^{2} = 12^{2}$

$a^{2} + 16 = 144$

$a^{2} = 128$ , czyli $a = 8 \sqrt{2}$

Wobec tego pole trójkąta wynosi:

$P = \frac{8 \sqrt{2} \cdot 4}{2} = 16 \sqrt{2}$

Przykład 2

Obliczymy pole trójkąta równobocznego, w którym promień okręgu opisanego na tym trójkącie ma długość $4 \sqrt{3}$ .

Rozwiązanie:

Do rozwiązania zadania wykorzystamy wzór na pole trójkąta równobocznego, gdy dana jest długość promienia okręgu opisanego na tym trójkącie:

$P = \frac{3 \sqrt{3} R^{2}}{4}$

Ponieważ $R = 4 \sqrt{3}$ , zatem:

$P = \frac{3 \sqrt{3} \cdot {(4 \sqrt{3})}^{2}}{4} = \frac{3 \sqrt{3} \cdot 48}{4} = 36 \sqrt{3}$

Przykład 3

Obliczymy długość okręgu opisanego na trójkącieokrąg opisany na trójkącieokręgu opisanego na trójkącie równoramiennym o podstawie długości $8$ i ramionach długości $10$ .

Rozwiązanie:

Narysujmy trójkąt równoramienny, okrąg na nim opisany oraz wprowadźmy oznaczenia, jak na rysunku. Promień okręgu opisanego na trójkącie jest odcinkiem łączącym wierzchołek trójkąta z punktem, w którym przecinają się symetralne boków trójkąta.

RiNBKG8VrTLx0

Ilustracja przedstawia trójkąt równoramienny o bokach długości 10 oraz podstawie długości osiem wpisany w okrąg. Zaznaczono promień okręgu.

Niech

$a = 8$

$b = c = 10$

Do wyznaczenia pola trójkąta, wykorzystamy wzór Herona:

$P = \sqrt{p (p - a) (p - b) (p - c)}$ , gdzie $p = \frac{a + b + c}{2}$

Zatem $p = \frac{8 + 10 + 10}{2} = 14$ .

Wobec tego $P = \sqrt{14 \cdot (14 - 8) \cdot (14 - 10) \cdot (14 - 10)} = \sqrt{14 \cdot 6 \cdot 4 \cdot 4} = 8 \sqrt{21}$ .

Ponieważ pole trójkąta możemy obliczyć ze wzoru $P = \frac{a b c}{4 R}$ , gdzie $R$ jest promieniem okręgu opisanego na trójkącie, zatem po przekształceniu wzoru na pole trójkąta mamy:

$R = \frac{a b c}{4 P}$

$R = \frac{8 \cdot 10 \cdot 10}{32 \sqrt{21}} = \frac{100}{4 \sqrt{21}} = \frac{25 \sqrt{21}}{21}$

Długość okręgu opisanego na tym trójkącie wynosi:

$L = 2 π \cdot R = 2 π \cdot \frac{25 \sqrt{21}}{21} = \frac{50 \sqrt{21}}{21} π$

Przykład 4

Wiadomo, że iloczyn sinusów kątów wewnętrznych w pewnym trójkącie wynosi $\frac{12}{25}$ , a pole tego trójkąta jest równe $6$ . Obliczymy długość promienia okręgu opisanego na tym trójkącie.

Rozwiązanie:

Jeżeli $α$ , $β$ , $γ$ są miarami kątów wewnętrznych opisywanego trójkąta, to z warunku podanego w zadaniu wynika, że

$\sin α \cdot \sin β \cdot \sin γ = \frac{12}{25}$ oraz

$P = 6$

Do wyznaczenia długości $R$ promienia okręgu opisanego na tym trójkącie wykorzystamy wzór na pole trójkąta:

$P = 2 R^{2} \sin α \sin β \sin γ$

$6 = 2 \cdot R^{2} \cdot \frac{12}{25}$

$R^{2} = \frac{25}{4}$ , czyli $R = \frac{5}{2}$

Przykład 5

Obliczymy długości boków trójkąta, w którym miara jednego z kątów wynosi $60 °$ , pole trójkąta wynosi $2 \sqrt{3}$ , a promień okręgu na tym trójkącie jest równy $4$ .

Rozwiązanie:

Narysujmy okrąg opisany na trójkącie i wprowadźmy oznaczenia, jak na rysunku.

R1Z8IkyKcIqPw

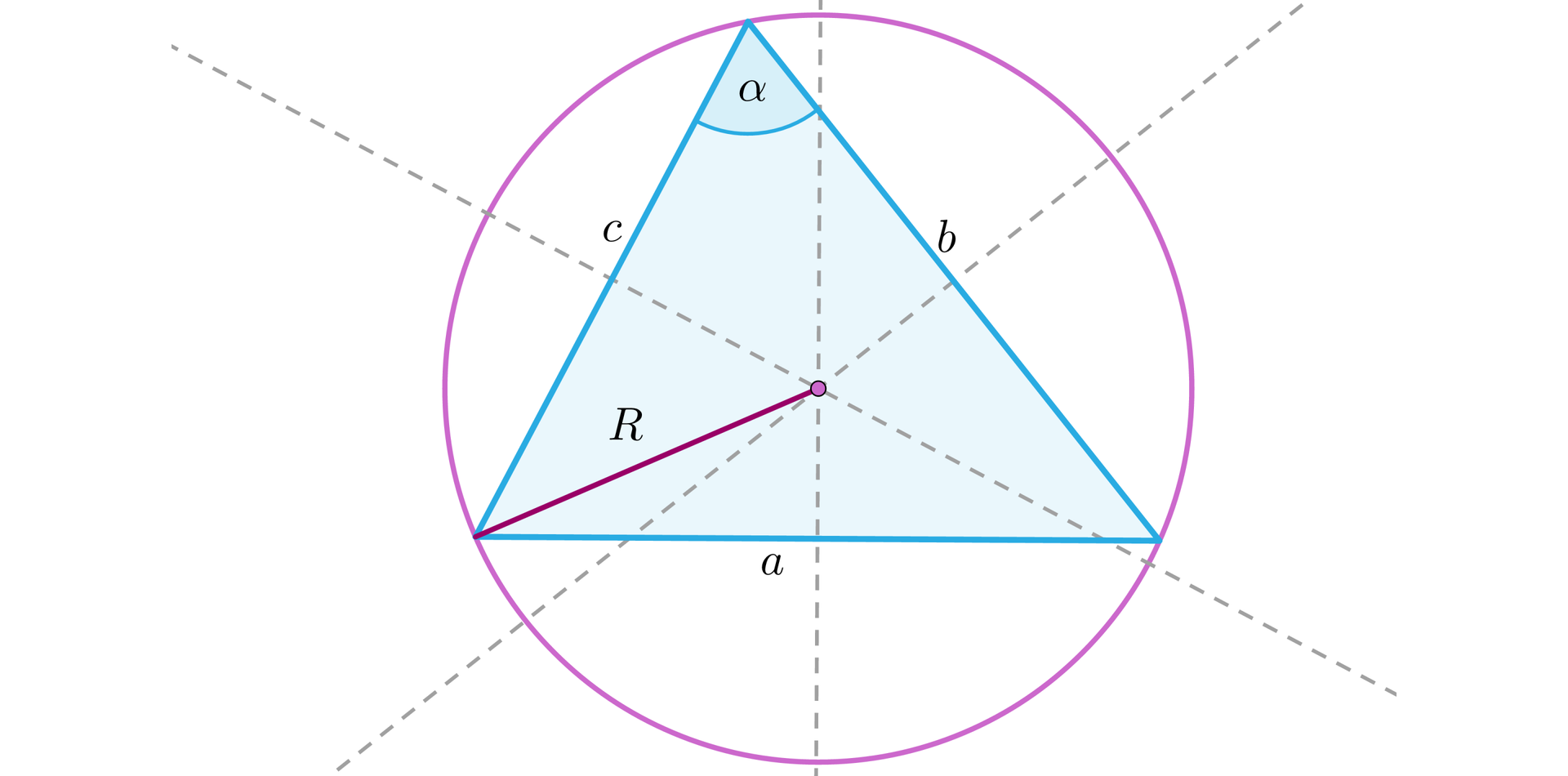
Ilustracja przedstawia trójkąt o bokach długości a b i c z kątem pomiędzy ramionami b i c o mierze alfa wpisany w okrąg. Zaznaczono promień R.

Ponieważ $α = 60 °$ oraz $R = 4$ , zatem:

korzystając z twierdzenia sinusów $\frac{a}{\sin α} = 2 R$ , czyli $a = 2 R \sin α$

$a = 2 \cdot 4 \cdot \frac{\sqrt{3}}{2} = 4 \sqrt{3}$

Zależność pomiędzy długościami boków $b$ i $c$ oraz polem trójkąta wyraża równanie:

$2 \sqrt{3} = \frac{1}{2} \cdot b \cdot c \cdot \sin 60 °$

Jeżeli wykorzystamy twierdzenie cosinusówtwierdzenie cosinusówtwierdzenie cosinusów, to:

${(4 \sqrt{3})}^{2} = b^{2} + c^{2} - 2 b c \cdot \cos 60 °$

Wobec tego do wyznaczenia długości boków $b$ i $c$ rozwiązujemy układ równań:

$\{\begin{cases} 2 \sqrt{3} = \frac{1}{2} \cdot b \cdot c \cdot \sin 60 ° \\ {(4 \sqrt{3})}^{2} = b^{2} + c^{2} - 2 b c \cdot \cos 60 ° \end{cases}$

$\{\begin{cases} 2 \sqrt{3} = \frac{1}{2} \cdot b \cdot c \cdot \frac{\sqrt{3}}{2} \\ 48 = b^{2} + c^{2} - 2 b c \cdot \frac{1}{2} \end{cases}$

$\{\begin{cases} 8 = b c \\ 48 = b^{2} + c^{2} - b c \end{cases}$

$\{\begin{cases} b = \frac{8}{c} \\ 48 = b^{2} + c^{2} - 8 \end{cases}$

Rozwiązujemy równanie z jedną niewiadomą:

${(\frac{8}{c})}^{2} + c^{2} - 56 = 0$

$c^{4} - 56 c^{2} + 64 = 0$

$c = \sqrt{28 - 12 \sqrt{5}}$ lub $c = \sqrt{28 + 12 \sqrt{5}}$

Zatem $b = \frac{8}{\sqrt{28 - 12 \sqrt{5}}} = \frac{2 \sqrt{28 - 12 \sqrt{5}}}{7 - 3 \sqrt{5}}$ lub $b = \frac{8}{\sqrt{28 + 12 \sqrt{5}}} = \frac{2 \sqrt{28 + 12 \sqrt{5}}}{7 + 3 \sqrt{5}}$

Istnieją dwa trójkąty spełniające warunki zadania:

trójkąt o bokach długości $4 \sqrt{3}$ , $\frac{2 \sqrt{28 - 12 \sqrt{5}}}{7 - 3 \sqrt{5}}$ oraz $\sqrt{28 - 12 \sqrt{5}}$ ,
trójkąt o bokach długości $4 \sqrt{3}$ , $\frac{2 \sqrt{28 + 12 \sqrt{5}}}{7 + 3 \sqrt{5}}$ , $\sqrt{28 + 12 \sqrt{5}}$

Słownik

okrąg opisany na trójkącie

okrąg, na którym leżą wszystkie wierzchołki tego trójkąta

twierdzenie sinusów

w dowolnym trójkącie stosunek długości dowolnego boku do sinusa kąta leżącego naprzeciwko tego boku jest stały i równy podwojonej długości promienia okręgu opisanego na tym trójkącie

twierdzenie cosinusów

w dowolnym trójkącie, kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi

Wprowadzenie

Animacja

Pole trójkąta równobocznego, na którym opisano okrąg o promieniu $R$

Przeciwprostokątna trójkąta prostokątnego, na którym opisano okrąg o promieniu $R$

Pole dowolnego trójkąta, na którym opisano okrąg o promieniu $R$

Słownik

Wprowadzenie

Animacja

Przeczytaj

Pole trójkąta równobocznego, na którym opisano okrąg o promieniu R

Przeciwprostokątna trójkąta prostokątnego, na którym opisano okrąg o promieniu R

Pole dowolnego trójkąta, na którym opisano okrąg o promieniu R

Słownik

Pole trójkąta równobocznego, na którym opisano okrąg o promieniu $R$

Przeciwprostokątna trójkąta prostokątnego, na którym opisano okrąg o promieniu $R$

Pole dowolnego trójkąta, na którym opisano okrąg o promieniu $R$