Przeczytaj
Ciąg, podobnie jak każdą funkcję, nazywamy monotonicznym, jeżeli jest rosnący, malejący, stały, nierosnący albo niemalejący.
W przypadku takich ciągów, z reguły łatwo zauważyć wyraźną zależność między wyrazami ciągu.
Wykres nieskończonego ciągu zawarty jest w wykresie funkcji liniowej przedstawionym na rysunku.
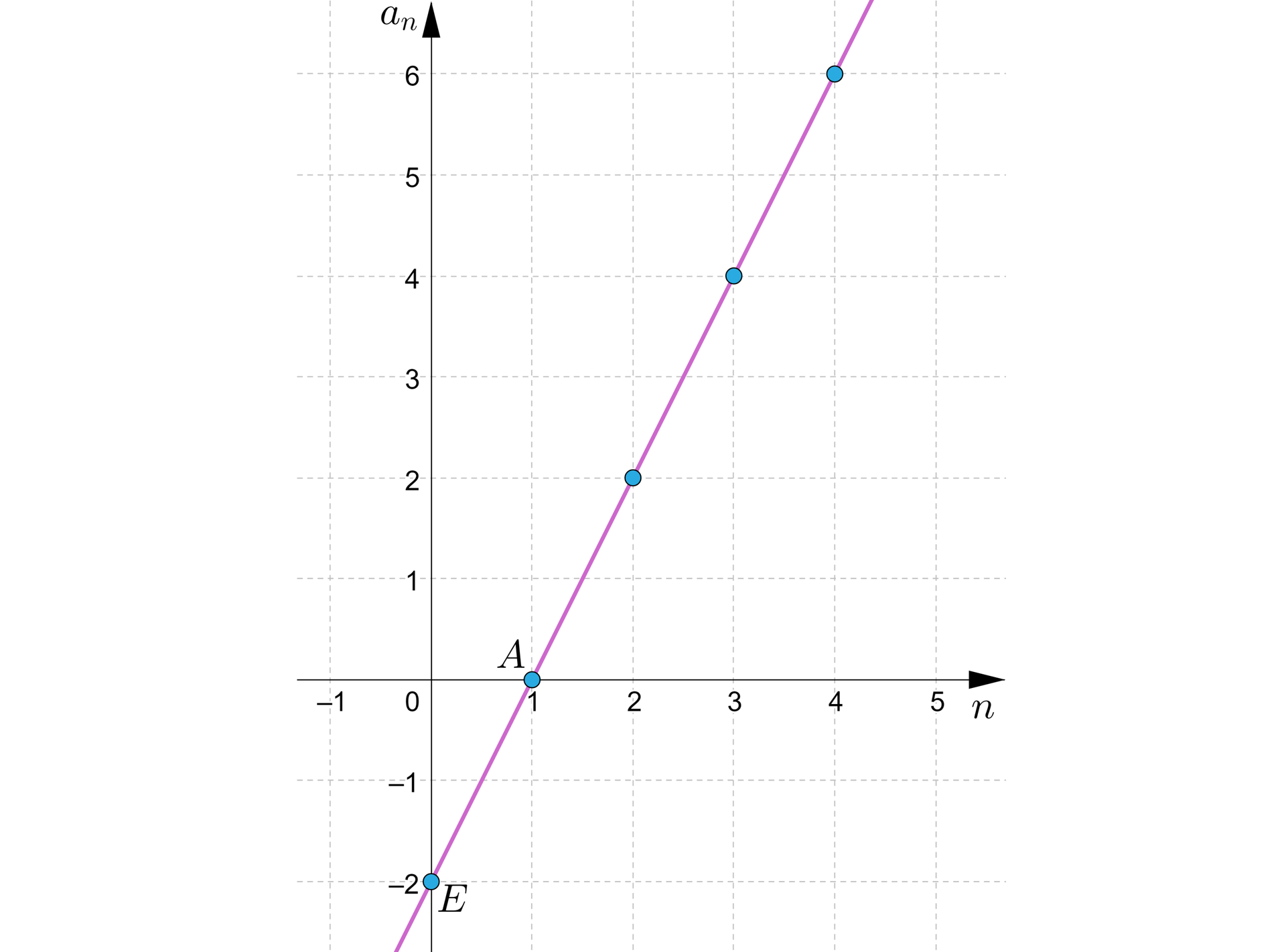
Na podstawie wykresu możemy odczytać kolejne wyrazy ciągu:
, , , ,
Wnioskujemy, że różnica między kolejnymi wyrazami ciągu jest stała i równa , czyli ciąg jest rosnący.
Aby to udowodnić, określimy najpierw wzór funkcji . Wykres tej funkcji przechodzi przez punkty
i . Zatem współrzędne każdego z tych punktów spełniają równanie
Rozwiązujemy układ równań
Stąd i .
Zatem .
Wynika z tego, że wzór ogólny ciągu ma postać .
Obliczamy różnicę między kolejnymi wyrazami ciągu.
- ciąg rosnący.
Zauważmy, że różnica między kolejnymi wyrazami ciągu jest równa współczynnikowi kierunkowemu prostej, w której zawarty jest wykres ciągu.
Wykres nieskończonego ciągu zawarty jest w wykresie funkcji liniowej przedstawionym na rysunku.

Na podstawie wykresu możemy odczytać kolejne wyrazy ciągu:
, , , , , ,
Wnioskujemy, że różnica między kolejnymi wyrazami jest stała i równa , czyli ciąg jest malejący.
Aby to udowodnić, określimy najpierw wzór funkcji . Wykres tej funkcji przechodzi przez punkty i . Zatem współrzędne każdego z tych punktów spełniają równanie
Rozwiązujemy układ równań.
Stąd i .
Zatem .
Wynika z tego, że wzór ogólny ciągu ma postać .
Obliczamy różnicę między kolejnymi wyrazami ciągu.
– ciąg malejący.
Zauważmy, że różnica między kolejnymi wyrazami ciągu jest równa współczynnikowi kierunkowemu prostej, w której zawarty jest wykres ciągu.
Korzystając z rozważań zawartych w powyższych przykładach, możemy zapisać:
jeśli wykres ciągu jest zawarty w wykresie funkcji liniowej , to dla ciąg jest rosnący, a dla ciąg jest malejący.
Podobny wniosek możemy zapisać, gdy znamy wzór ogólny ciągu.
Ciąg określony wzorem ogólnym jest dla każdej liczby rzeczywistej
rosnący, gdy ,
malejący, gdy ,
stały, gdy .
Rozważmy dwa ciągi. Ciąg określony wzorem ogólnym i ciąg określony wzorem ogólnym .
Początkowe wyrazy ciągu to: , , , ,
Początkowe wyrazy ciągu to: , , , ,
Ciąg jest ciągiem malejącym, a ciąg jest ciągiem rosnącym i .
Wniosek
Jeżeli ciąg jest ciągiem malejącym, to ciąg określony wzorem ogólnym jest ciągiem rosnącym.
Istotnie, jeśli ciąg jest ciągiem malejącym, to .
Mnożąc obie strony tej nierówności przez , otrzymujemy
, czyli to ,
co oznacza, że ciąg jest ciągiem rosnącym.
Podobny wniosek można zapisać, gdy ciąg jest ciągiem rosnącym.
Wniosek
Jeżeli ciąg jest ciągiem rosnącym, to ciąg określony wzorem ogólnym jest ciągiem malejącym.
Ciągi rosnące i malejące nazywamy ciągami ściśle monotonicznymi.
Ciągi monotoniczneCiągi monotoniczne, to nie tylko ciągi ściśle monotoniczne, ale też ciągi nierosnące i niemalejące.
Uzasadnimy, że ciąg określony wzorem ogólnym jest ciągiem niemalejącym.
Przypomnijmy, że to część całkowita liczby . Czyli największa liczba całkowita nie większa od .
Na przykład:
Zatem jeśli jest liczbą parzystą, to jest liczbą całkowitą i .
Jeśli liczba jest liczbą nieparzystą, to .
Możemy więc zapisać, że jeśli i to
Czyli dla każdej liczby naturalnej dodatniej prawdziwa jest nierówność , co dowodzi, że ciąg jest niemalejący.
Ciąg rosnący posiada wyraz najmniejszy. Czyli każdy wyraz takiego ciągu jest większy od pewnej liczby rzeczywistej. O takim ciągu mówimy, że jest ograniczony z dołu.
Mówimy, że ciąg jest ograniczony z dołu, jeżeli istnieje taka liczba rzeczywista , że dla każdej liczby naturalnej dodatniej spełniona jest nierówność .
Ciąg malejący posiada wyraz największy. Czyli każdy wyraz takiego ciągu jest mniejszy od pewnej liczby rzeczywistej. O takim ciągu mówimy, że jest ograniczony z góry.
Mówimy, że ciąg jest ograniczony z góry, jeżeli istnieje taka liczba rzeczywista , że dla każdej liczby naturalnej dodatniej spełniona jest nierówność .
Ciąg nazywamy ograniczonym, jeśli istnieją dwie takie liczby rzeczywiste i , że dla każdej liczby naturalnej spełniona jest nierówność:
Liczby i nazywamy odpowiednio ograniczeniem dolnym i górnym ciągu.
Wykażemy, że ciąg określony wzorem
jest ograniczony.
Wypisujemy kilka początkowych wyrazów ciągu.
, , , , ,
Możemy zapisać przypuszczalny wzór na –ty wyraz ciągu
.
Sprawdzamy swoje przypuszczenia.
Czyli znaleziony wzór jest poprawny.
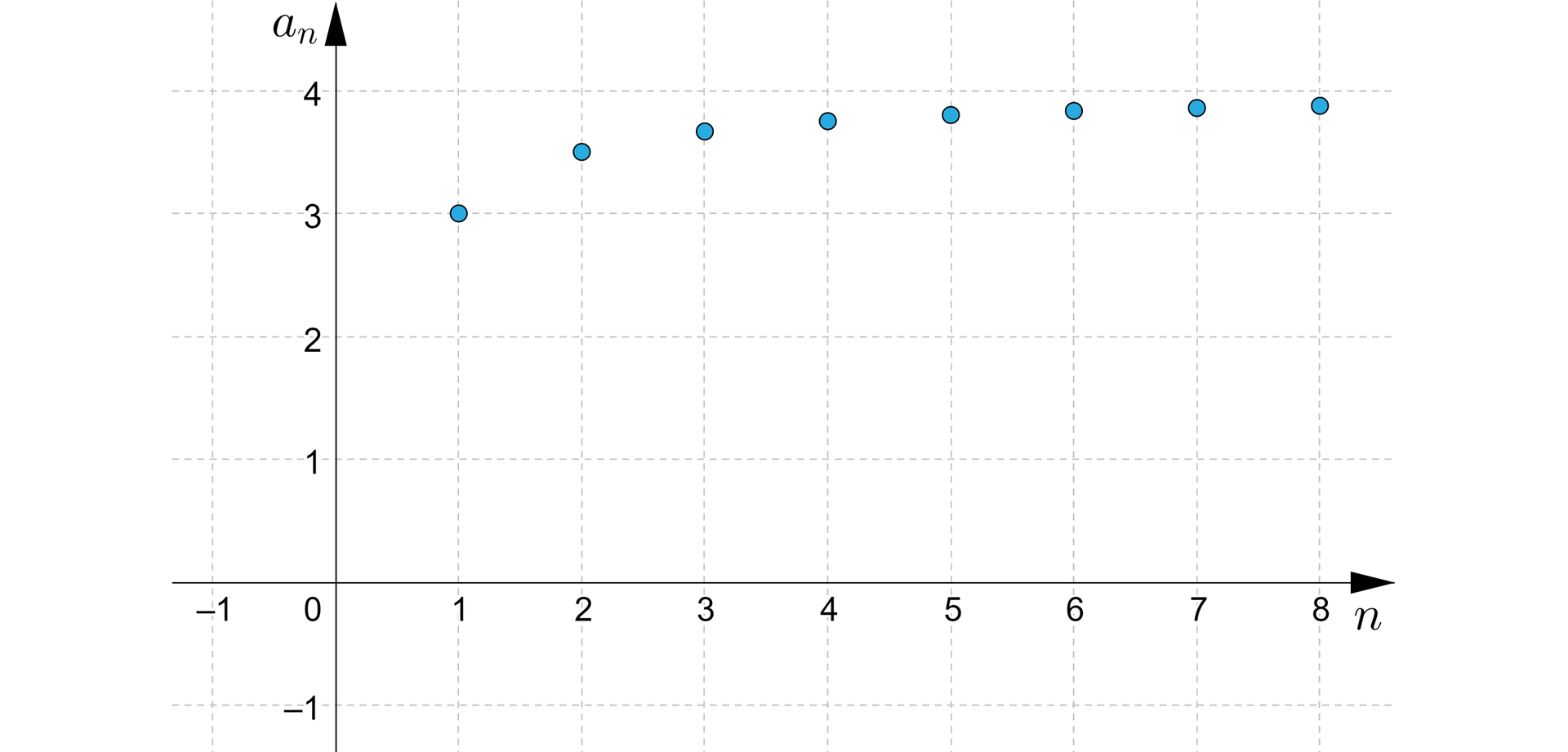
Na podstawie powyższych rozważań zauważamy, że ciąg jest ciągiem rosnącym. Najmniejszy wyraz tego ciągu to , a największy to . A zatem jest to ciąg ograniczony.
Liczba ograniczająca ten ciąg z góry to na przykład , a liczba ograniczająca ciąg z dołu to na przykład .
Słownik
ciąg określony wzorem ogólnym jest dla każdej liczby rzeczywistej
rosnący, gdy ,
malejący, gdy ,
stały, gdy