Przeczytaj
Lazare Carnot udowodnił twierdzenie sformułowane w Elementach Euklidesa w trzecim wieku przed naszą erą, które brzmiało:
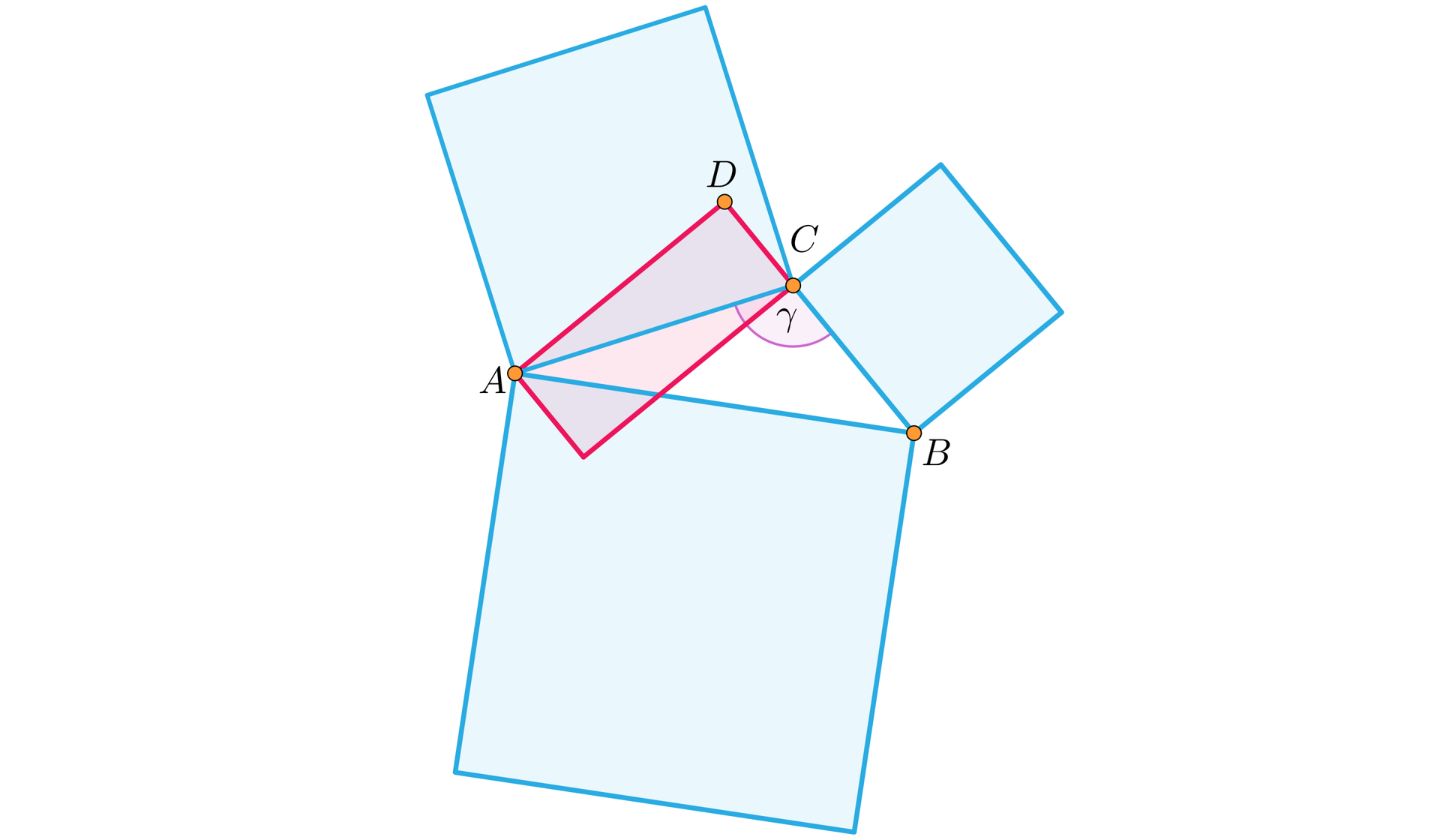
W trójkącie rozwartokątnym kwadrat na boku leżącym naprzeciwko kąta rozwartego jest większy od kwadratów na bokach zawierających kąt rozwarty o dwukrotność prostokąta zbudowanego na boku, na który spada prosta prostopadła i na odcinku odciętym na zewnątrz przez tę prostopadłą w kierunku kąta rozwartego.
Pierwsze twierdzenie Carnota sformułowane we współczesnym języku i opisujące również przypadek trójkąta ostrokątnego brzmi następująco:
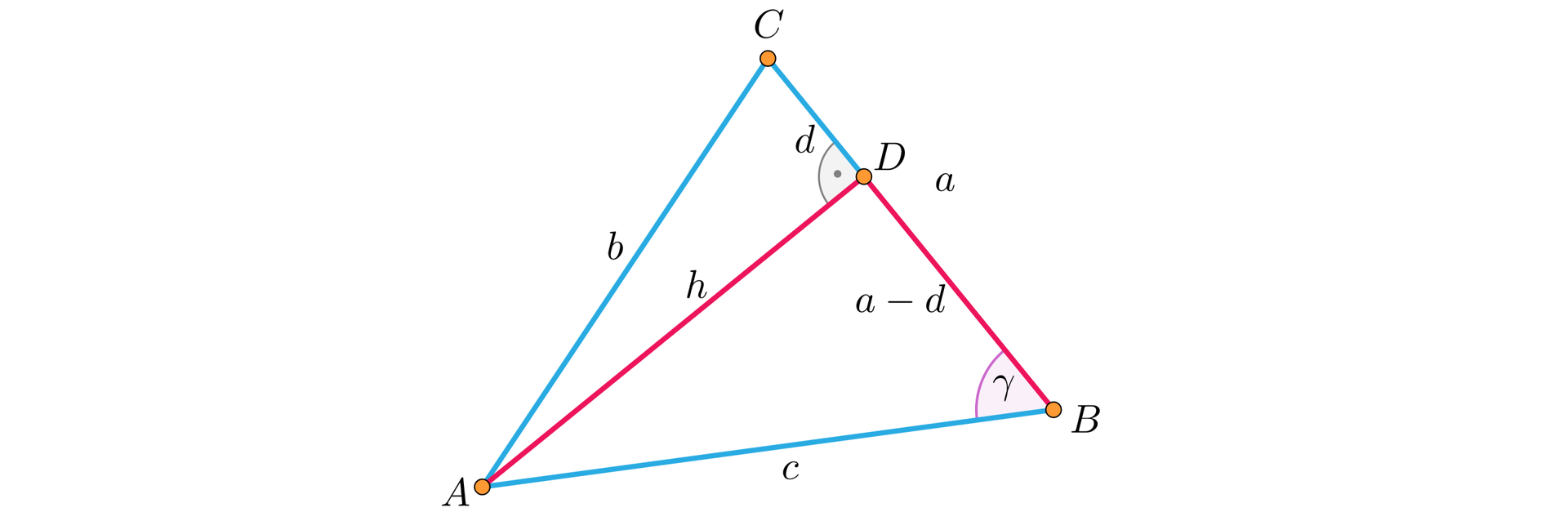
1. Jeżeli w trójkącie kąt jest ostry i punkt jest spodkiem wysokościspodkiem wysokości opuszczonej z wierzchołka , to lub równoważnie .

2. Jeżeli w trójkącie kąt jest rozwarty i punkt jest spodkiem wysokości opuszczonej z wierzchołka , to lub równoważnie .
1. Załóżmy, że w trójkącie kąt jest ostry i punkt jest spodkiem wysokości opuszczonej z wierzchołka . Ponieważ trójkąty i są trójkątami prostokątnymi, to , .
Stąd , więc .
2. Załóżmy, że w trójkącie kąt jest rozwarty i punkt jest spodkiem wysokości opuszczonej z wierzchołka . Ponieważ trójkąty i są trójkątami prostokątnymi, to , .
Stąd , więc .
W trójkącie , kąt przy wierzchołku jest ostry oraz , . Ponadto, odległość spodka wysokości opuszczonej na bok od wierzchołka wynosi . Wyznaczymy długość boku .
Z powyższego twierdzenia wynika, że . Stąd .
W trójkącie , kąt przy wierzchołku jest rozwarty oraz , . Ponadto, odległość spodka wysokości opuszczonej na bok od wierzchołka wynosi . Wyznaczymy długość boku .
Z powyższego twierdzenia wynika, że . Stąd .
Kolejnym twierdzeniem przypisywanym Carnotowi jest wniosek z powyższego twierdzenia nazywany twierdzeniem cosinusów.
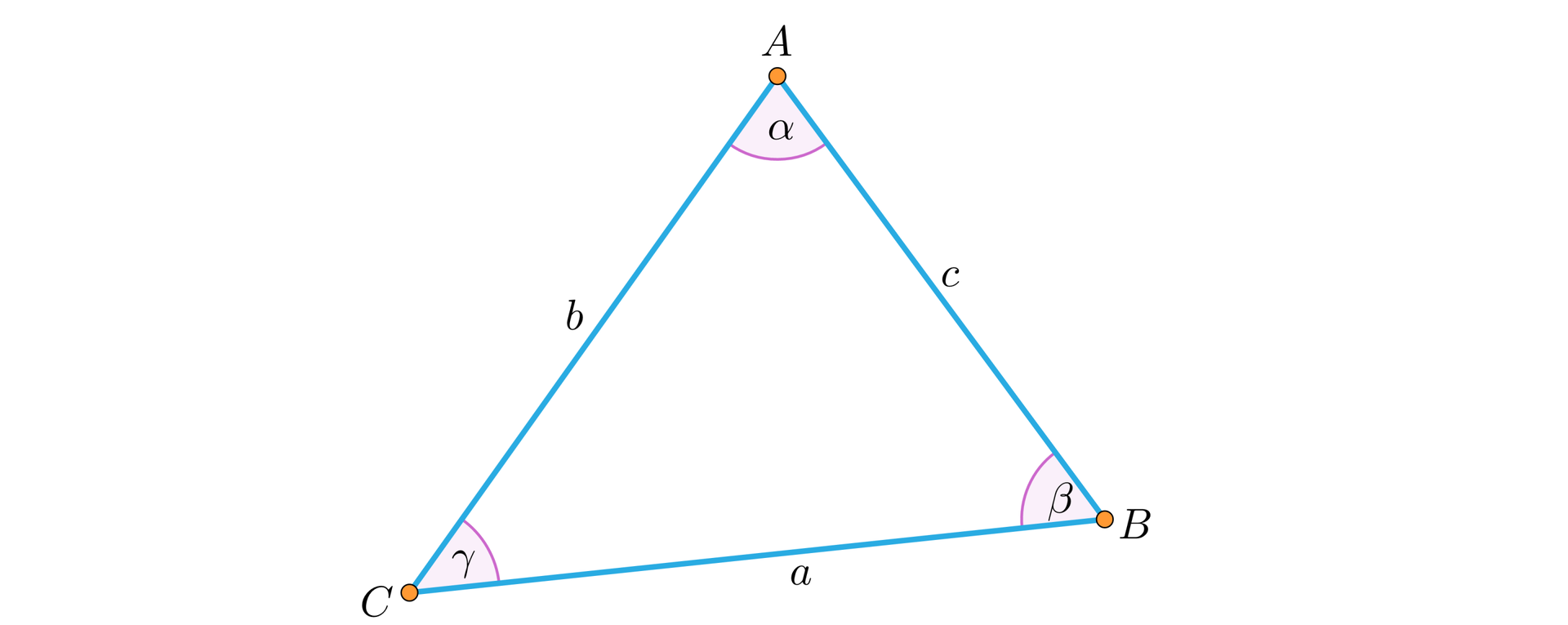
W dowolnym trójkącie , przy oznaczeniach z rysunku mamy:
Niech będzie punktem, w którym wysokość poprowadzona z wierzchołka opada na bok . Trójkąty i są trójkątami prostokątnymi niezależnie od tego czy kąt jest ostry czy rozwarty.
Jeżeli kąt jest ostry, to .
Po wstawieniu do równości dostajemy .
Jeżeli kąt jest rozwarty, to .
Po wstawieniu do równości dostajemy .
Jeżeli kąt jest prosty, to i . Wtedy .
W trójkącie dane są boki , oraz kąt między nimi . Wyznaczymy długość boku .
Z twierdzenia cosinusów mamy:
Stąd .
Z twierdzenia Carnota i twierdzenia Pitagorasa wynika, że
Jeżeli , , są długościami boków trójkąta, to kąt między bokami , jest
ostry wtedy i tylko wtedy, gdy .
prosty wtedy i tylko wtedy, gdy .
rozwarty wtedy i tylko wtedy, gdy .
Ciekawostka
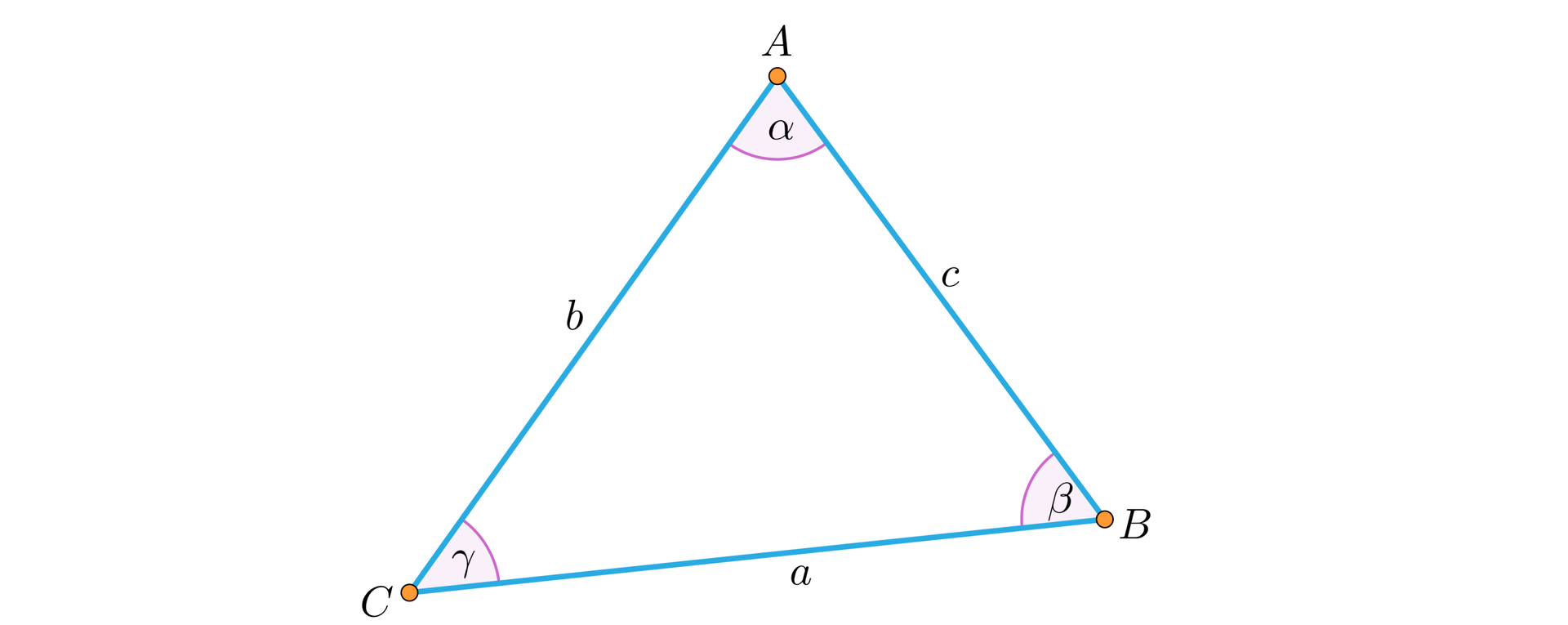
W dowolnym trójkącie , przy oznaczeniach z rysunku mamy , gdzie oznacza funkcję .
Z twierdzenia cosinusów mamy
Z drugiej strony .
Jeżeli jest kątem ostrym, to oraz , więc .
Jeżeli jest kątem rozwartym, to oraz , więc .
Jeżeli jest kątem prostym, to oraz , więc .
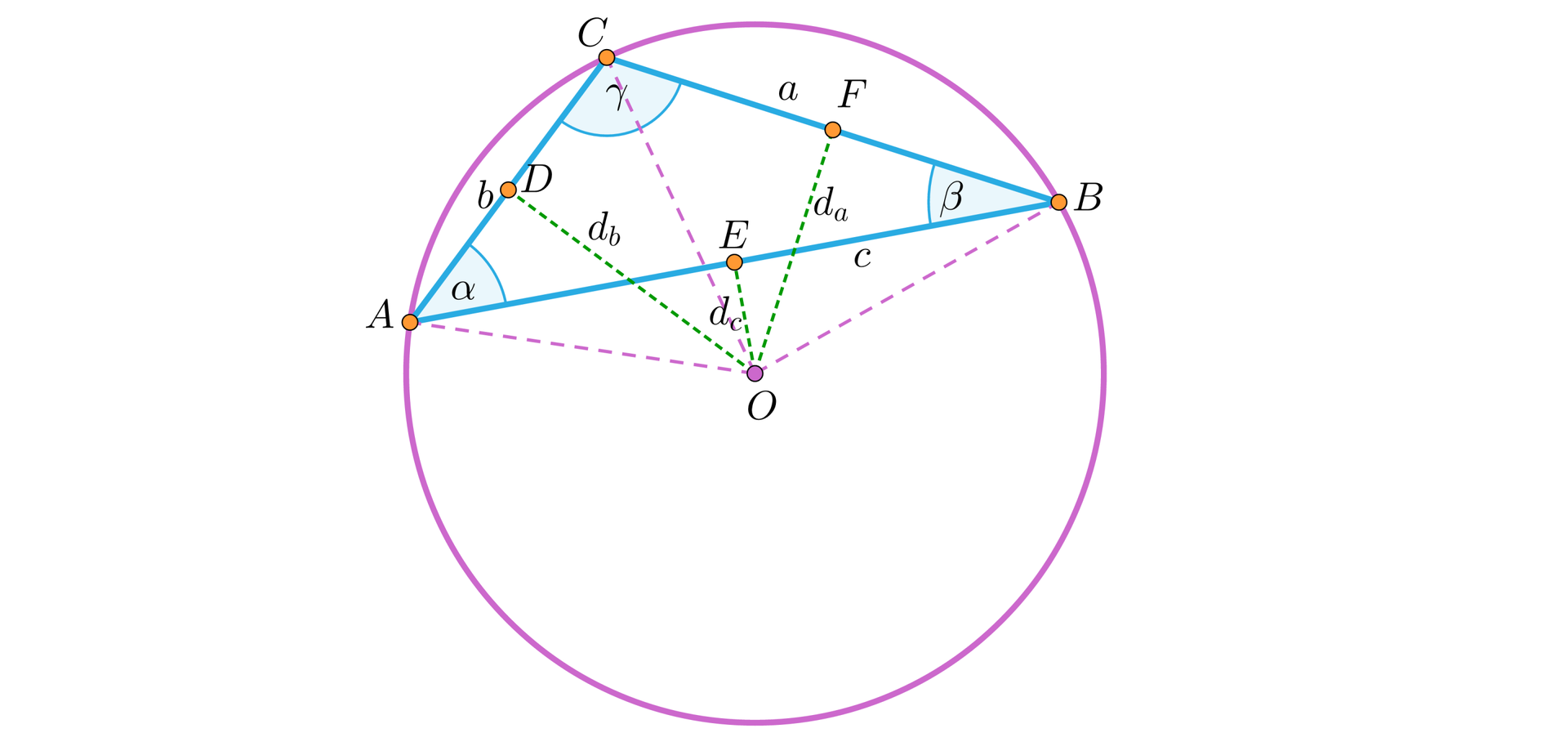
Ustalmy, że i oznaczają promienie okręgów, odpowiednio, wpisanego w trójkąt i opisanego na trójkącieopisanego na trójkącie oraz kąty i boki trójkąta oznaczone są jak na rysunku. Wyznaczymy zależności między kątami , , a kątami , i .

Rozważmy kąty jakie tworzą z bokami trójkąta promienie , , okręgu opisanego na trójkącie .
Z własności okręgu opisanego na trójkącie, trójkąty , i są równoramienne i ich ramionami są promienie .
Niech , , oznaczają kąty przy podstawie trójkątów równoramiennych , i , odpowiednio.
Jeżeli trójkąt jest ostrokątny, to , , .

Dodając stronami mamy , więc .
Dalej , więc . Stąd .
Analogicznie, oraz .
Jeżeli trójkąt jest rozwartokątny i kąt jest rozwarty, to , , .

Dodając stronami dwie pierwsze równości mamy , więc i ostatecznie .
Dalej , więc .
Analogicznie, .
Jeżeli trójkąt jest prostokątny i kąt jest prosty, to , , .
Dodając stronami dwie pierwsze równości mamy , więc i ostatecznie .
Dalej , więc .
Analogicznie,
Warto zauważyć, że powyższe zależności między kątami trójkąta i kątami , , wynikają z twierdzenia o kącie środkowym i wpisanym w okrąg.
Omówimy sposób wyznaczenia okręgu opisanego na trójkącie, w którym znany jest jeden kąt ostry i bok leżący naprzeciwko tego kąta, bez wyznaczania symetralnych boków trójkąta.
Przy oznaczeniach powyżej niech będzie danym kątem ostrym.

Wtedy na mocy cechy przystawania kąt‑bok‑kąt możemy wyznaczyć trójkąt . Jego wierzchołek będzie środkiem okręgu opisanego na trójkącie . Wiemy, że i znamy bok i to wystarczy do konstrukcji trójkąta .
Przytoczymy teraz dwa twierdzenia, które wykorzystują własności wysokościwysokości w trójkącie i są niezbędne do sformułowania drugiego twierdzenia Carnota.
, gdzie oznacza pole trójkąta .
, gdzie jest środkiem okręgu wpisanego w trójkąt.
Ponieważ promień jest prostopadły do boku trójkąta, to , więc . Stąd .
, gdzie oznacza pole trójkąta .
Niech , , oznaczają odległości środka okręgu opisanego na trójkącieokręgu opisanego na trójkącie od odpowiednich boków trójkąta. Odległości te są również wysokościami w trójkątach , , .
Po skorzystaniu z własności sinusa i cosinusa w trójkącie prostokątnym oraz wyznaczonych kątów , , powyżej mamy, w przypadku trójkąta ostrokątnego:
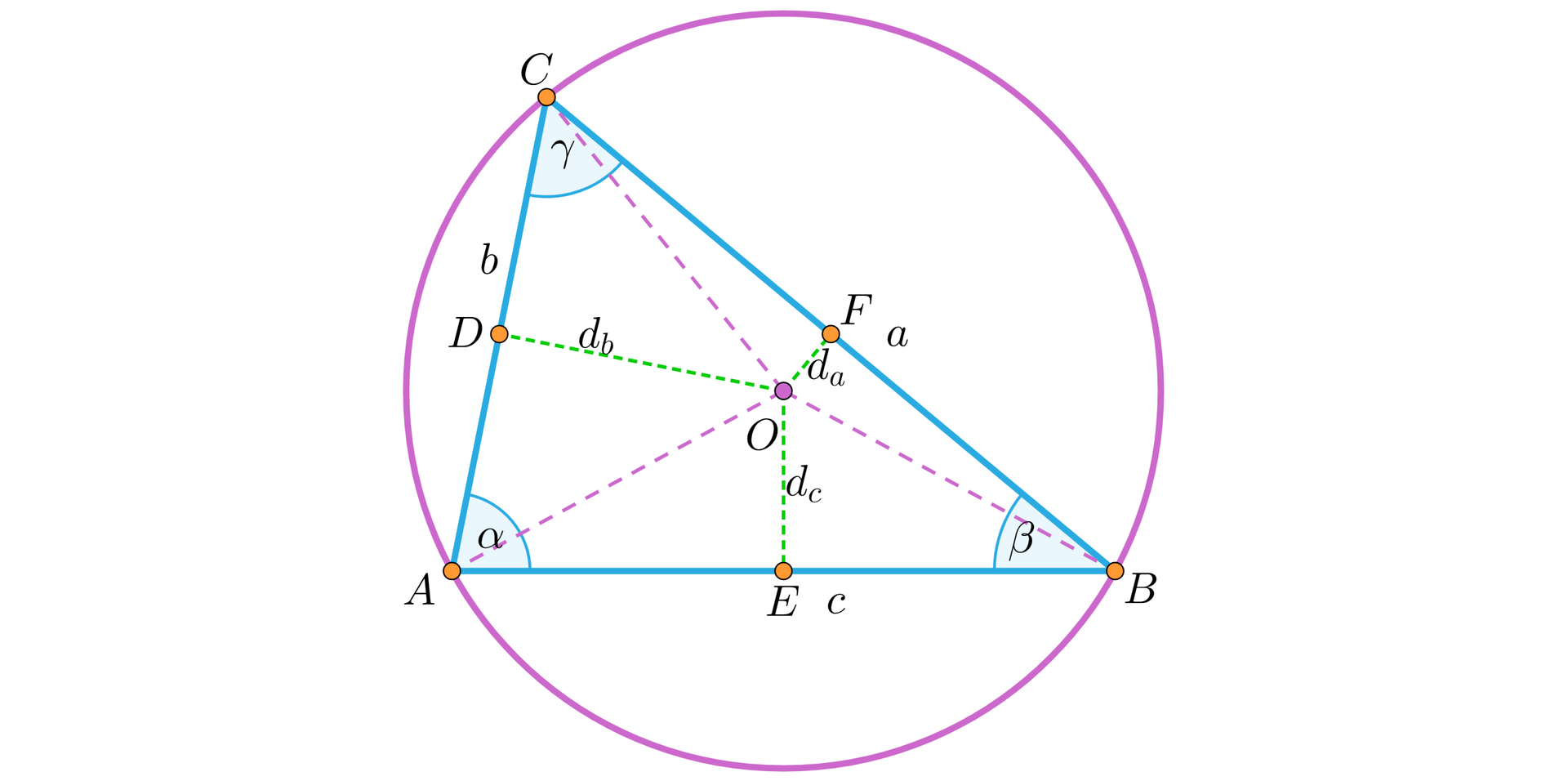
,
,
.
Stąd .
W przypadku trójkąta rozwartokątnego, w którym kąt jest rozwarty mamy:
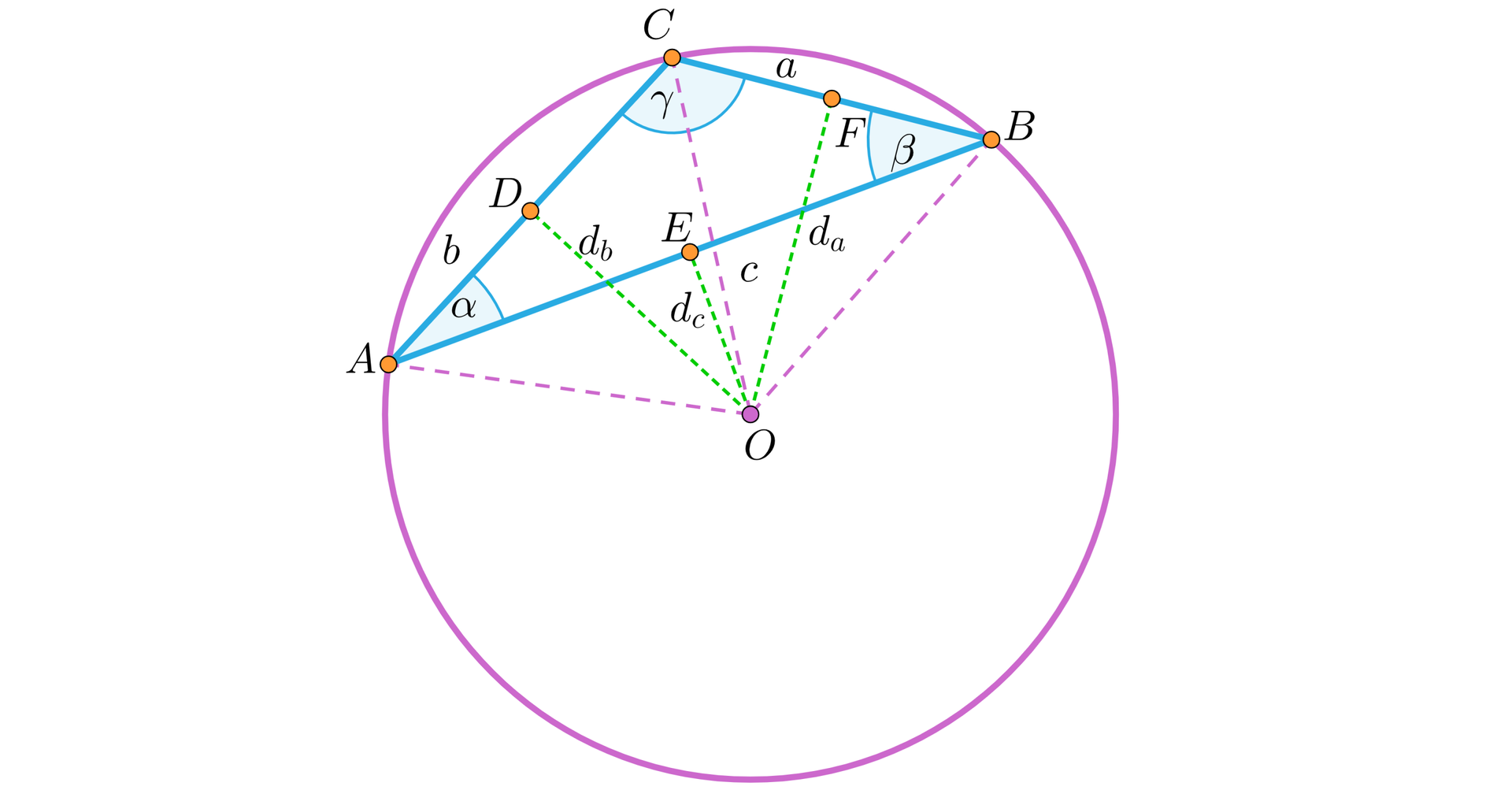
,
,
.
.
Stąd .
W przypadku trójkąta prostokątnego, w którym kąt jest prosty mamy:
,
,
.
.
Stąd .
Dla dowolnego trójkąta zachodzi .
Z dwóch poprzednich twierdzeń wynika, że:
Jeśli trójkąt jest ostrokątny, to wykorzystując wysokości w trójkącie mamy:

, , .
W przypadku, gdy kąt jest rozwarty lub prosty to wykorzystując wysokości w trójkącie mamy:
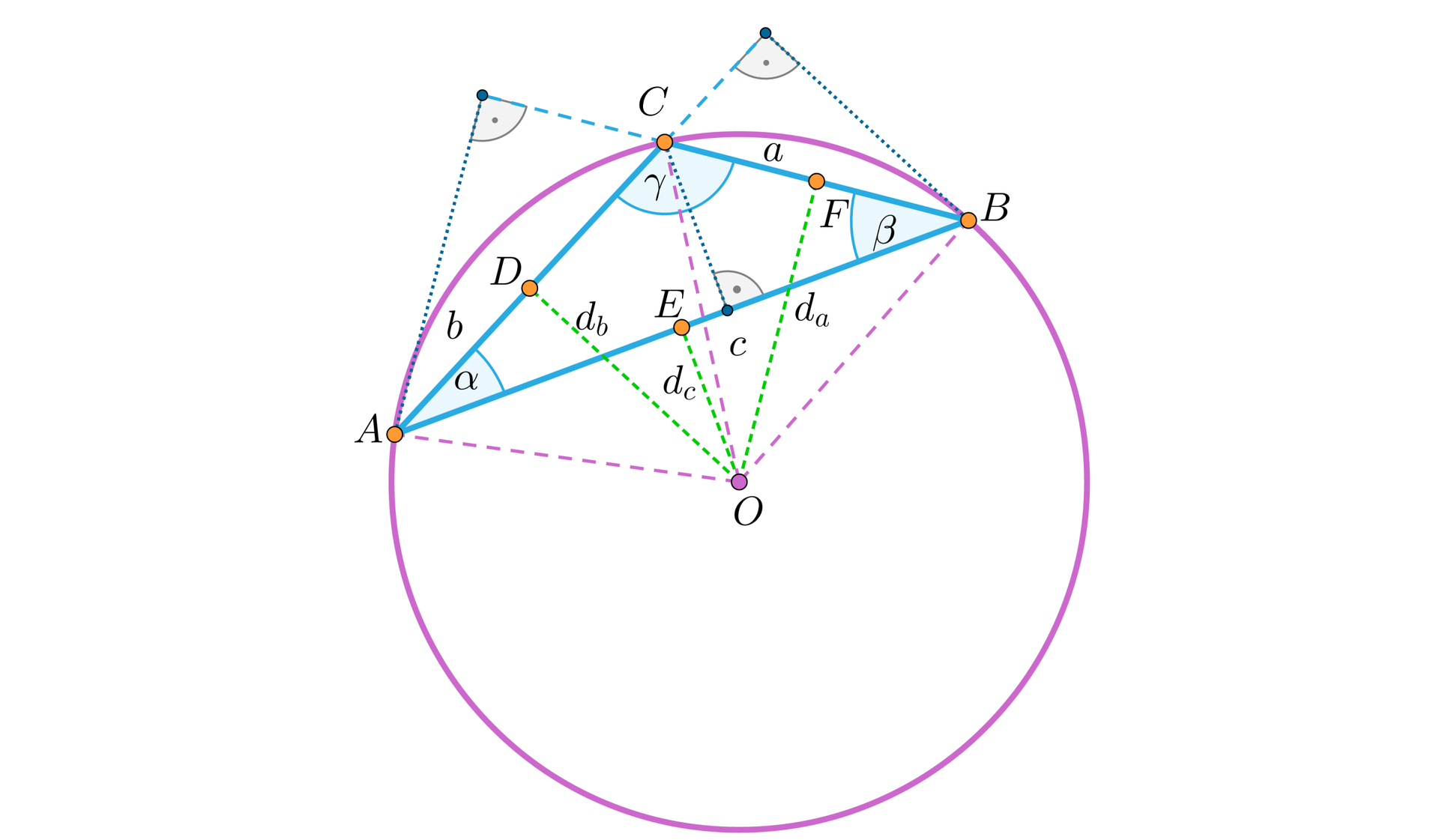
,
,
.
Wtedy .
Przekształcamy licznik:
Ostatecznie:
Wyznaczymy długość promienia okręgu wpisanego w trójkątokręgu wpisanego w trójkąt , jeśli oraz , .
Wyznaczamy cosinusy kątów trójkąta
Trzeci kąt trójkąta wynosi , więc
Wtedy
Przy oznaczeniach z rysunków:
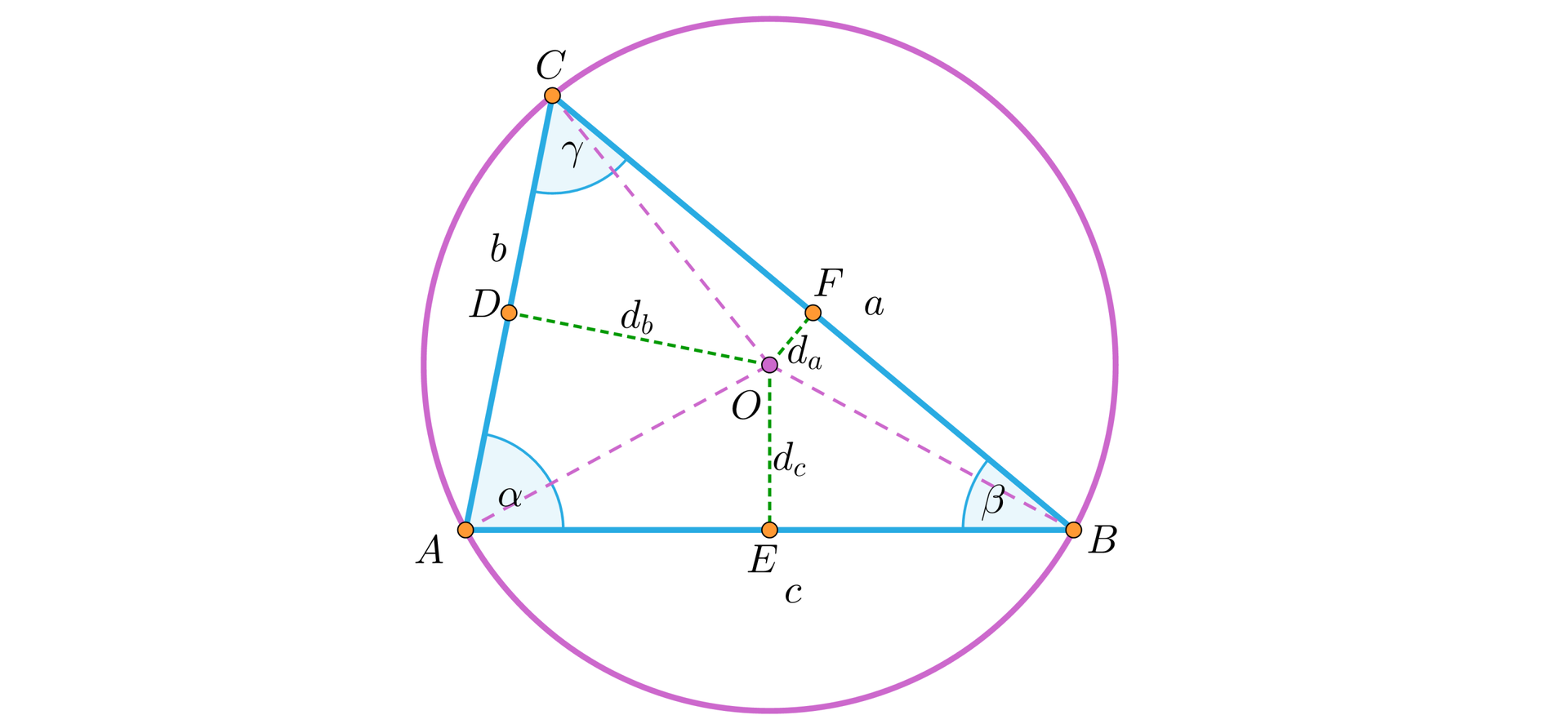
Jeśli trójkąt jest ostrokątny, to .
Jeśli trójkąt jest trójkątem rozwartokątnym, w którym kąt jest rozwarty, to .
Jeśli trójkąt jest trójkątem prostokątnym, w którym kąt jest prosty, to .
W dowodzie twierdzenia o długości promienia wyznaczyliśmy:
w przypadku, gdy trójkąt jest ostrokątny , , .
Stąd
.
w przypadku, gdy trójkąt jest trójkątem rozwartokątnym, w którym kąt jest rozwarty , , .
Stąd
.
w przypadku, gdy trójkąt jest trójkątem prostokątnym, w którym kąt jest prosty: , , .
Stąd
Wyznaczymy długość promienia okręgu wpisanego w prostokątny trójkątokręgu wpisanego w prostokątny trójkąt .

Środek okręgu opisanego na trójkącie prostokątnym jest środkiem przeciwprostokątnej, stąd . Odcinki i są odległościami , środka okręgu opisanego na trójkącie od boków i , odpowiednio.
Zauważamy, że trójkąty , i są podobne na mocy cechy kąt – kąt – kąt. Stąd , .
Z drugiego twierdzenia Carnota .
Słownik
najkrótszy odcinek łączący jeden z wierzchołków trójkąta z prostą zawierającą przeciwległy bok trójkąta (podstawę)
punkt przecięcia wysokości z podstawą
okrąg, który jest styczny do wszystkich boków trójkąta
okrąg, który przechodzi przez wszystkie wierzchołki trójkąta