Przeczytaj

W trakcie lekcji omówimy sposoby wyznaczania równania prostej symetrycznej do prostej o zadanym równaniu względem początku układu współrzędnych, czyli punktu o współrzędnych $(0, 0)$ .

Do wyznaczania równań prostych w symetrii względem punktu $(0, 0)$ wykorzystamy definicję punktów symetrycznych względem początku układu współrzędnychpunktów symetrycznych względem początku układu współrzędnych.

punkty symetryczne względem początku układu współrzędnych

Definicja: punkty symetryczne względem początku układu współrzędnych

Punktem symetrycznym do punktu $P$ o współrzędnych $P = (x, y)$ względem początku układu współrzędnych jest punkt $P'$ o współrzędnych $P' = (- x, - y)$ .

Punktami symetrycznymi względem punktu $(0, 0)$ są na przykład punkty o współrzędnych:

$P = (- 3, 2)$ oraz $P' = (3, - 2)$ ,
$P = (2, 5)$ oraz $P' = (- 2, - 5)$ ,
$P = (0, 4)$ oraz $P' = (0, - 4)$ .

Ważne!

Obrazem punktu $P = (0, 0)$ w symetrii względem początku układu współrzędnych jest ten sam punkt.

W celu wyznaczenia równania prostej w symetrii względem początku układu współrzędnych posłużymy się równaniem ogólnym oraz równaniem kierunkowym prostej.

I. Wyznaczenie równania prostej symetrycznej względem początku układu współrzędnych, gdy mamy dane:

punkt przecięcia prostej z osią $X$ ,
punkt przecięcia prostej z osią $Y$ ,
równanie w postaci ogólnej.równanie prostej w postaci ogólnejpostaci ogólnej.

Określimy prostą w postaci ogólnej za pomocą równania $A x + B y + C = 0$ .

Załóżmy, że współczynniki $A$ , $B$ , $C$ są różne od $0$ .

Wtedy punkt przecięcia tej prostej z osią $X$ ma współrzędne $K = (- \frac{C}{A}, 0)$ , a punkt przecięcia z osią $Y$ ma współrzędne $L = (0, - \frac{C}{B})$ .

Opiszmy prostą symetryczną względem początku układu współrzędnych za pomocą równania ogólnego $A' x + B' y + C' = 0$ .

Załóżmy, że współczynniki $A'$ , $B'$ , $C'$ są różne od $0$ .

Zatem do tej prostej należą punkty o współrzędnych $K' = (\frac{C}{A}, 0)$ oraz $L' = (0, \frac{C}{B})$ .

Podstawimy współrzędne tych punktów do równania ogólnego tej prostej. Otrzymujemy układ równań:

$\{\begin{cases} A' \cdot \frac{C}{A} + B' \cdot 0 + C' = 0 \\ A' \cdot 0 + B' \cdot \frac{C}{B} + C' = 0 \end{cases}$ .

Jeżeli pierwsze równanie pomnożymy przez $A$ , a drugie przez $B$ , to otrzymamy układ równań:

$\{\begin{cases} A' C + A C' = 0 \\ B' C + B C' = 0 \end{cases}$ .

Zatem $A' = - \frac{A C'}{C}$ oraz $B' = - \frac{B C'}{C}$ .

Jeżeli podstawimy obliczone współczynniki do równania prostej symetrycznej, to otrzymujemy równanie:

$- \frac{A C'}{C} x - \frac{B C'}{C} y + C' = 0$ .

Mnożąc obie strony równania przez ułamek $- \frac{C}{C'}$ , otrzymujemy równanie prostej symetrycznej do prostej $A x + B y + C = 0$ względem początku układu współrzędnych:

$A x + B y - C = 0$ .

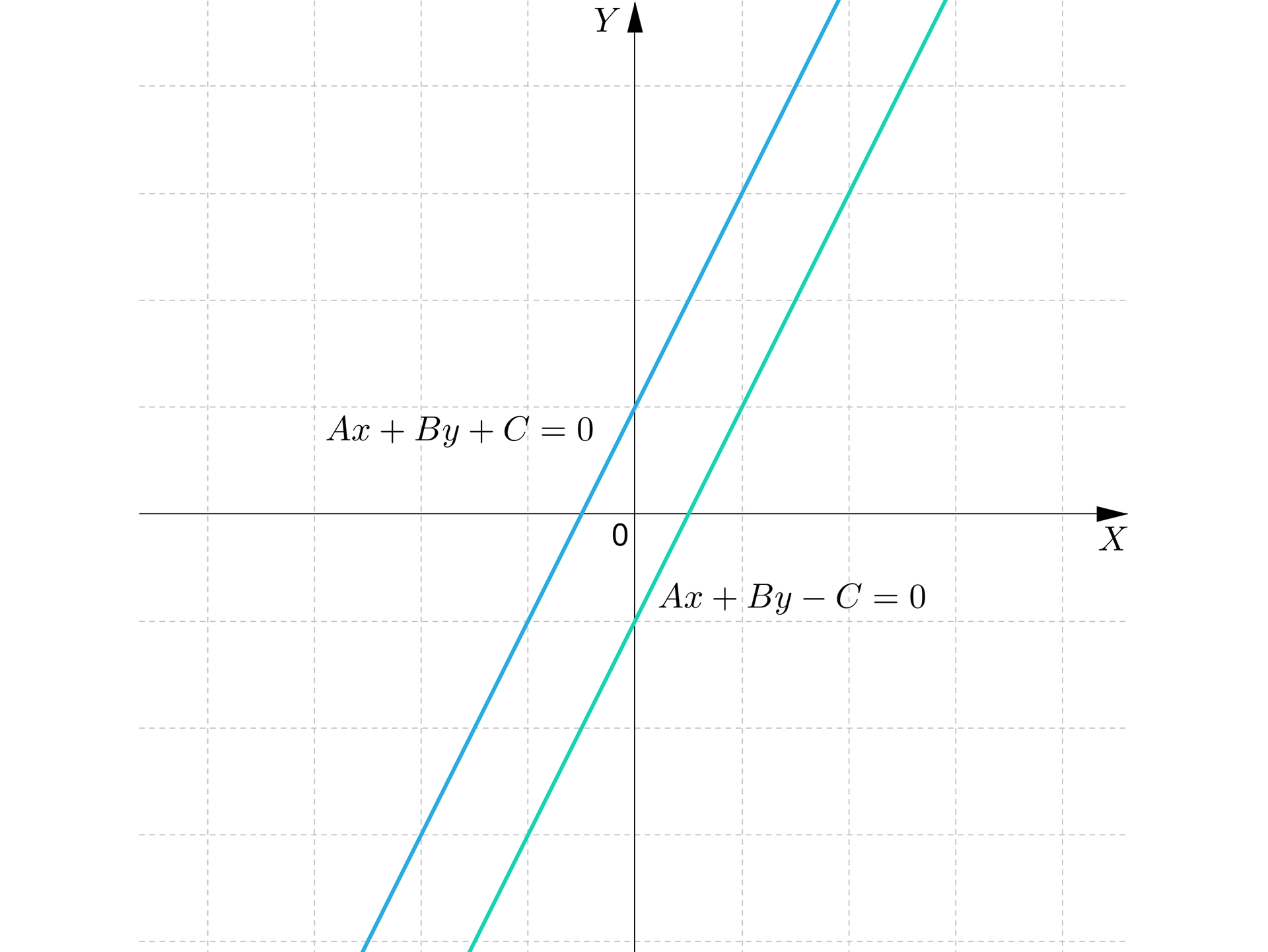
Na rysunku przedstawiono wykresy prostych symetrycznych względem początku układu współrzędnych:

RIGazpGKdooZG

Grafika przedstawia poziomą oś x oraz pionową oś y. Na płaszczyźnie znajdują się dwie ukośne proste, które są równoległe do siebie. Pierwsza z nich ma równanie Ax+By+C=0 i przechodzi przez pierwszą, drugą i trzecią ćwiartkę, przecinając oś y na wysokości punktu początek nawiasu, 0, 1, zamknięcie nawiasu . Druga z nich ma równanie Ax+By-C=0 i przechodzi przez pierwszą, czwartą i trzecią ćwiartkę, prosta przecina oś y w punkcie początek nawiasu, 0, minus 1, zamknięcie nawiasu.

II. Wyznaczenie równania prostej symetrycznej względem początku układu współrzędnych, gdy mamy dane:

punkt przecięcia z osią $X$ ,
punkt przecięcia z osią $Y$ ,
równanie w postaci kierunkowejpostaci kierunkowej.

Określimy prostą w postaci kierunkowej za pomocą równania $y = a x + b$ .

Wtedy punkt przecięcia tej prostej z osią $X$ ma współrzędne $P = (- \frac{b}{a}, 0)$ , a punkt przecięcia z osią $Y$ ma współrzędne $Q = (0, b)$ .

Obrazem punktu $P$ w symetrii względem początku układu współrzędnych jest punkt o współrzędnych $P' = (\frac{b}{a}, 0)$ , a obrazem punktu $Q$ jest punkt $Q' = (0, - b)$ .

Zapiszmy równanie prostej symetrycznej względem punktu $(0, 0)$ w postaci $y = a' x + b'$ .

Podstawimy współrzędne punktów $P'$ oraz $Q'$ do równania tej prostej. Otrzymujemy układ równań:

$\{\begin{cases} 0 = a' \cdot \frac{b}{a} + b' \\ - b = a' \cdot 0 + b' \end{cases}$ .

Z układu równań obliczamy, że $a' = a$ oraz $b' = - b$ , zatem równanie prostej symetrycznej do prostej $y = a x + b$ względem początku układu współrzędnych zapisujemy w postaci: $y = a x - b$ .

Wnioski:

proste opisane równaniami $x = a$ oraz $x = - a$ , gdzie $a \in ℝ$ są zawsze symetryczne względem początku układu współrzędnych;
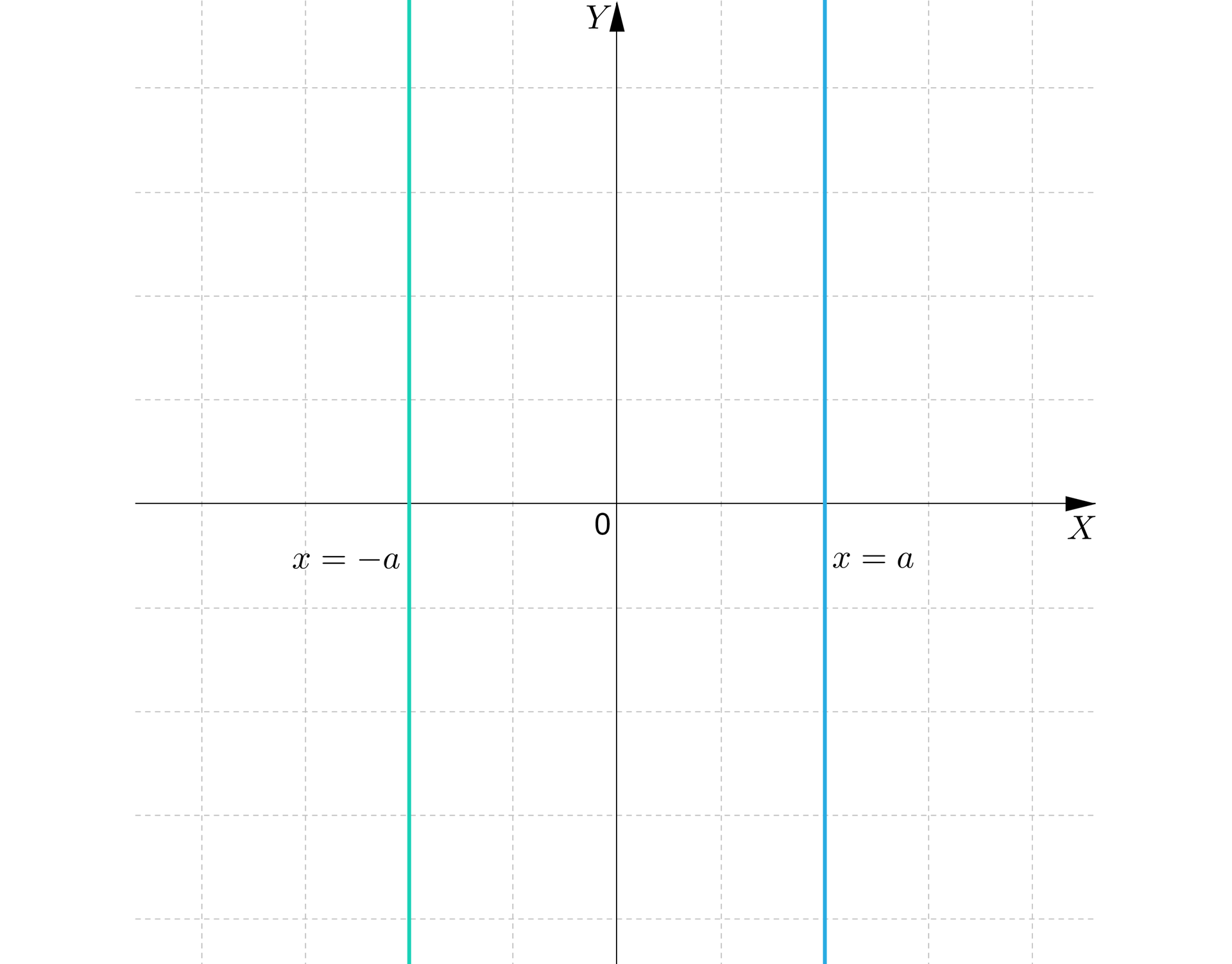
proste opisane równaniami $y = b$ oraz $y = - b$ , gdzie $b \in ℝ$ są zawsze symetryczne względem początku układu współrzędnych;
obrazem prostej opisanej za pomocą równania $y = a x$ w symetrii względem początku układu współrzędnych jest ta sama prosta.

Na rysunkach przedstawiono wykresy prostych symetrycznych względem początku układu współrzędnych:

RTIzKm7f45C8y

Grafika przedstawia poziomą oś x oraz pionową oś y. Na płaszczyźnie znajdują się pionowe proste, które są równoległe do siebie. Pierwsza z nich ma równanie x=-a i przecina oś x w punkcie początek nawiasu, minus 2, 0, zamknięcie nawiasu. Druga z nich ma równanie x=a i przecina oś x w punkcie początek nawiasu, 2, 0, zamknięcie nawiasu.

RATmnk6kjkexz

Grafika przedstawia poziomą oś x oraz pionową oś y. Na płaszczyźnie znajdują się poziome proste, które są równoległe do siebie. Pierwsza z nich ma równanie y=b i przecina oś y w punkcie początek nawiasu, 0, 3, zamknięcie nawiasu. Druga z nich ma równanie y=-b i przecina oś x w punkcie początek nawiasu, 0, minus 3 zamknięcie nawiasu.

Do wyznaczenia równania prostej w postaci kierunkowej wystarczy znać współrzędne dwóch dowolnych punktów, które należą do tej prostej.

Do wyznaczenia równania prostej symetrycznej względem początku układu współrzędnych wystarczy znaleźć obrazy w symetrii względem punktu $(0, 0)$ tych dwóch dowolnych punktów, a następnie wyznaczyć równanie prostej przechodzącej przez te punkty.

Przykład 1

Wyznaczymy równanie prostej w symetrii względem punktu o współrzędnych $(0, 0)$ do prostej o równaniu $y = 4 x - 1$ .

Rozwiązanie

Zauważmy, że do podanej prostej należą punkty o współrzędnych $A = (0, - 1)$ oraz $B = (1, 3)$ .

Obrazem tych punktów w symetrii względem początku układu współrzędnych są punkty o współrzędnych $A' = (0, 1)$ oraz $B' = (- 1, - 3)$ .

Oznaczmy równanie prostej w symetrii względem osi $Y$ w postaci $y = a' x + b'$ .

Podstawiamy do tego równania współrzędne punktów $A'$ oraz $B'$ i otrzymujemy układ równań:

$\{\begin{cases} 1 = 0 \cdot a' + b' \\ - 3 = - 1 \cdot a' + b' \end{cases}$ .

Rozwiązaniem układu równań jest para liczb $a' = 4$ oraz $b' = 1$ .

Zatem prosta symetryczna względem początku układu współrzędnych jest opisana za pomocą równania $y = 4 x + 1$ .

Przykład 2

Wyznaczymy równania prostych symetrycznych względem początku układu współrzędnych do prostych określonych równaniami:

a) $- x + 3 y + 2 = 0$ ,

b) $y = 2 x + 4$ .

Rozwiązanie

a) Równanie ogólne prostej symetrycznej do danej prostej względem początku układu współrzędnych jest postaci $- x + 3 y - 2 = 0$ .

b) Równanie kierunkowe prostej symetrycznej do danej prostej względem początku układu współrzędnych jest postaci $y = 2 x - 4$ .

Jeżeli wiemy, jakie warunki muszą spełniać współczynniki w równaniach prostych w symetrii względem początku układu współrzędnych, wówczas możemy znajdować wartości parametrów, dla których te proste są symetryczne względem punktu $(0, 0)$ .

Przykład 3

Wyznaczymy, dla jakich wartości parametrów $p$ i $q$ proste o równaniach $y = (p - q) x + 4$ oraz $y = 3 x + (2 p + 3 q)$ są symetryczne względem początku układu współrzędnych.

Rozwiązanie

Proste o podanych równaniach są symetryczne względem początku układu współrzędnych, gdy zachodzi układ równań:

$\{\begin{cases} p - q = 3 \\ 2 p + 3 q = - 4 \end{cases}$ .

Rozwiązaniem układu równań są liczby $p = 1$ oraz $q = - 2$ .

Dla otrzymanych wartości parametrów $p$ i $q$ proste są symetryczne względem początku układu współrzędnych.

Przykład 4

Wyznaczymy, dla jakich wartości parametru $m$ proste o równaniach $y = 2 x + m^{2}$ oraz $y = 2 x + (m - 2)$ są symetryczne względem początku układu współrzędnych.

Rozwiązanie

Wiadomo, że proste o równaniach w postaci kierunkowej są symetryczne względem początku układu współrzędnych, gdy ich współczynniki $b$ są liczbami przeciwnymi.

Zatem rozwiązujemy równanie:

$m^{2} = - (m - 2)$ .

Równanie przekształcamy do postaci $m^{2} + m - 2 = 0$ .

Rozwiązaniami tego równania są liczby $m = - 2$ lub $m = 1$ , zatem proste są symetryczne względem początku układu współrzędnych, gdy wartość $m$ jest równa jednej z otrzymanych liczb.

Słownik

równanie prostej w postaci ogólnej

równanie postaci $A x + B y + C = 0$ , gdzie $A$ i $B$ nie są jednocześnie równe $0$

równanie prostej w postaci kierunkowej

równanie postaci $y = a x + b$ , gdzie $a, b \in ℝ$ oraz $a$ nazywamy współczynnikiem kierunkowym prostej

punkty symetryczne względem początku układu współrzędnych

punkty o współrzędnych $P = (x, y)$ i $P' = (- x, - y)$

Wprowadzenie

Schemat interaktywny

Rozwiązanie

Rozwiązanie

Rozwiązanie

Rozwiązanie

Słownik