Rozwiążemy nierówność $x^2+x^4+x^6+...>\frac{4}{5}$, w której lewa strona jest sumą szeregu geometrycznego.

Rozwiązanie:

Szereg geometryczny ma pierwszy wyraz $a_1=x^2$ oraz iloraz $q=x^2$.

Zatem ten szereg jest zbieżny, gdy $x^2=0$ lub $\left|x^2\right|<1$.

Wobec tego dziedziną równania jest przedział $\left(-1,1\right)$.

Po obliczeniu sumy szeregu geometrycznegosuma szeregu geometrycznegosumy szeregu geometrycznego z lewej strony nierówności, przyjmuje ona postać:

$\frac{x^2}{1-x^2}>\frac{4}{5}$

Możemy nierówność pomnożyć stronami przez $\left(1-x^2\right)$, gdyż $1-x^2>0$:

$5x^2>4\left(1-x^2\right)$

$9x^2>4$

$x^2>\frac{4}{9}$

Otrzymujemy zatem rozwiązanie

$x>\frac{2}{3}$ lub $x<-\frac{2}{3}$, a po uwzględnieniu dziedziny nierówności dostajemy odpowiedź:

$x\in \left(-1,-\frac{2}{3}\right)\cup \left(\frac{2}{3},1\right)$.

Rozwiążemy nierówność $1+\sqrt{x}+{\left(\sqrt{x}\right)}^2+{\left(\sqrt{x}\right)}^3+{\left(\sqrt{x}\right)}^4+...<\sqrt{x}+1$, w której lewa strona jest sumą szeregu geometrycznegosuma szeregu geometrycznegosumą szeregu geometrycznego.

Rozwiązanie:

Zapiszmy założenie: $x\ge 0$.

Aby szereg geometryczny z lewej strony nierówności był zbieżny, musi zachodzić warunek: $\left|\sqrt{x}\right|<1$.

Stąd otrzymujemy ostateczną postać dziedziny nierówności: $\left.⟨0,1\right)$.

Po obliczeniu sumy szeregu geometrycznego z lewej strony nierówności, przyjmuje ona postać:

$\frac{1}{1-\sqrt{x}}\le \sqrt{x}+1$

Możemy pomnożyć nierówność stronami przez $\left(1-\sqrt{x}\right)$, gdyż $1-\sqrt{x}>0$.

Nierówność ma wówczas postać:

$1\le \left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)$

$1\le 1-x$

$x\le 0$

Zatem po uwzględnieniu dziedziny otrzymujemy rozwiązanie nierówności: $x=0$.

Rozwiążemy nierówność $\frac{1}{x-3}+\frac{1}{{\left(x-3\right)}^2}+\frac{1}{{\left(x-3\right)}^3}+...\ge 2-x$, w której lewa strona jest sumą szeregu geometrycznego.

Rozwiązanie:

Szereg geometryczny z lewej strony nierówności ma pierwszy wyraz $a_1=\frac{1}{x-3}$ i iloraz $q=\frac{1}{x-3}$.

Aby szereg był zbieżny, musi zachodzić warunek:

$\frac{1}{\left|x-3\right|}<1$.

Zatem

$1<\left|x-3\right|$

czyli

$x-3>1$ lub $x-3<-1$

Zatem dziedziną nierówności jest zbiór: $\left(-\infty ,2\right)\cup \left(4,\infty \right)$

Zapisujemy sumę szeregu geometrycznego:

$\frac{1}{x-3}\cdot \frac{1}{1-\frac{1}{x-3}}=\frac{1}{x-3}\cdot \frac{1}{\frac{x-3-1}{x-3}}=\frac{1}{x-3}\cdot \frac{x-3}{x-4}=\frac{1}{x-4}$

Zapisujemy nierówność z wykorzystaniem wzoru na sumę szeregu geometrycznego:

$\frac{1}{x-4}\le 2-x$

Przenosimy wszystkie wyrażenia na lewą stronę i sprowadzamy do wspólnego mianownika:

$\frac{1}{x-4}-2+x\le 0$

$\frac{1-\left(2-x\right)\left(x-4\right)}{x-4}\le 0$

$\frac{x^2-6x+9}{x-4}\le 0$

$\frac{{\left(x-3\right)}^2}{x-4}\le 0$

Nierówność tę zapisujemy równoważnie jako koniunkcję warunków:

${\left(x-3\right)}^2\left(x-4\right)\le 0$ i $x-4\ne 0$.

Rysujemy wykres wielomianu: $y={\left(x-3\right)}^2\left(x-4\right)$ i odczytujemy rozwiąznie:

$x\in \left(-\infty ,4\right)$

R1ZJVtfBSqvwN

Ilustracja przedstawia interpretację graficzną wielomianu. W układzie współrzędnych zaznaczono wykres wielomianu biegnący niemal pionowo przez drugą ćwiartkę od minus nieskończoności do miejsca zerowego, czyli x równa się trzy, stąd odbija w dół i w punkcie x równa się 4 przecina poziomą oś X, biegnąc dalej niemal pionowo do plus nieskończoności. Na osi X zaznaczono kolorem dziedzinę, czyli przedział otwarty od minus nieskończoności do czterech, przy czym punkt nawias 4, 0 zamknięcie nawiasu zaznaczono niezamalowanym kółkiem.

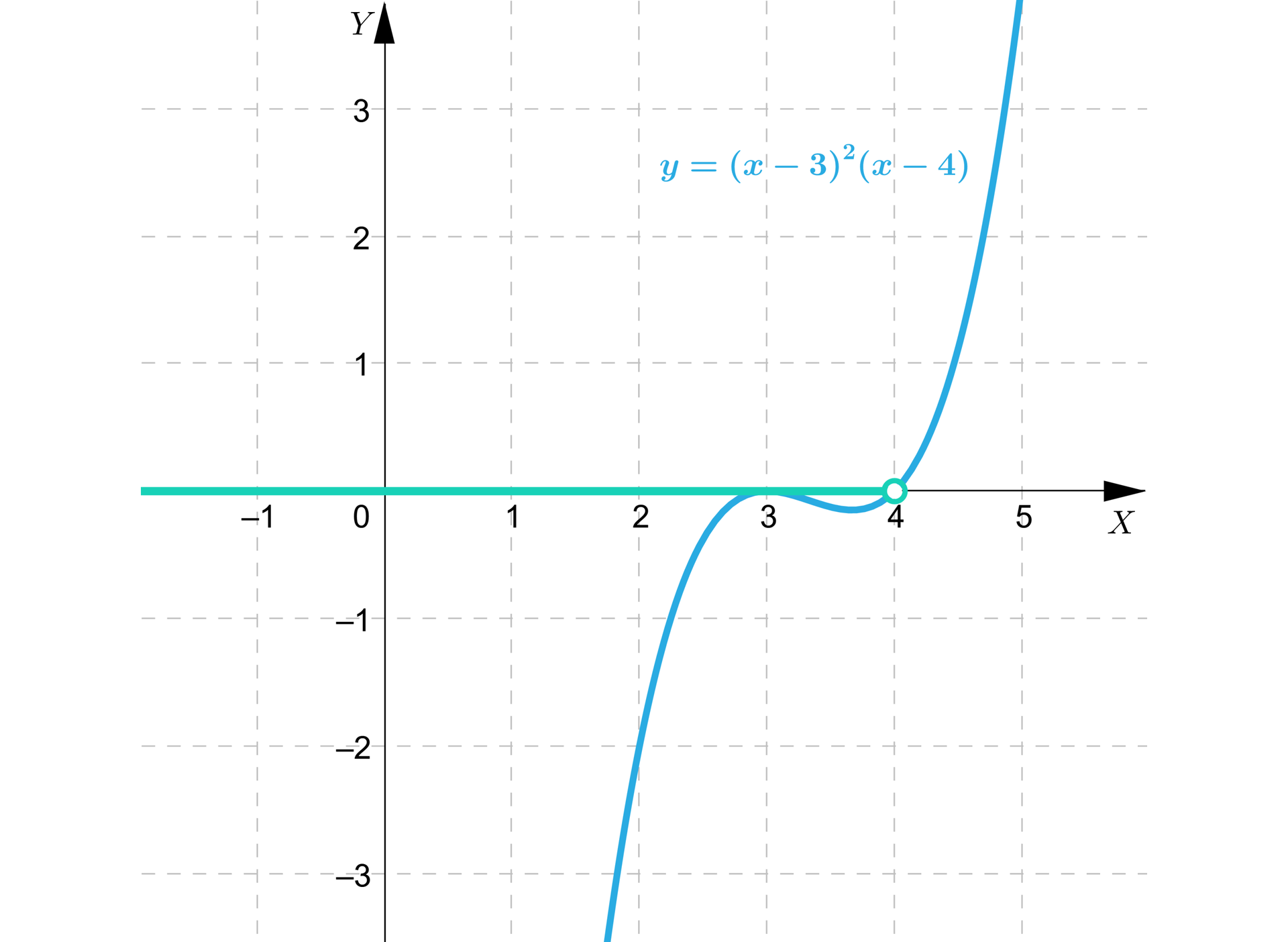
Po uwzględnieniu dziedziny nierówności rozwiązaniem jest przedział: $\left(-\infty ,2\right)$.

Rozwiążemy nierówność $\frac{1}{x-1}-\frac{1}{{\left(x-1\right)}^2}+\frac{1}{{\left(x-1\right)}^3}-...\le 4x+3$, w której lewa strona jest sumą szeregu geometrycznego.

Rozwiązanie:

Zakładamy, że $x\ne 1$.

Aby szereg geometryczny z lewej strony nierówności był zbieżny, musi zachodzić warunek:

$\left|-\frac{1}{x-1}\right|<1$

Otrzymujemy więc

$\left|x-1\right|>1$

$x-1>1$ lub $x-1<-1$

$x>2$ lub $x<0$

Zatem dziedzina nierówności jest zbiór $\left(-\infty ,0\right)\cup \left(2,\infty \right)$.

Zapisujemy sumę szeregu geometrycznego:

$\frac{\frac{1}{x-1}}{1+\frac{1}{x-1}}=\frac{\frac{1}{x-1}}{\frac{x}{x-1}}=\frac{1}{x}$.

Zatem nierówność przyjmuje postać:

$\frac{1}{x}\le 4x+3$.

Przenosimy wszystkie składniki na lewą stronę nierówności i sprowadzamy do wspólnego mianownika:

$\frac{1}{x}-\left(4x+3\right)\le 0$

$\frac{1-4x^2-3x}{x}\le 0$

Nierówność jest równoważna koniunkcji warunków:

$\left(1-4x^2-3x\right)x\le 0$ i $x\ne 0$.

Rozwiązujemy nierówność:

$\left(4x^2+3x-1\right)x\ge 0$

$∆=9+16=25$

$x=\frac{-3-5}{8}=-1$ lub $x=\frac{-3+5}{8}=\frac{1}{4}$

Rysujemy wykres wielomianu $y=\left(4x^2+3x-1\right)x$ i odczytujemy rozwiązanie:

$x\in ⟨-1,0⟩\cup \left.⟨\frac{1}{4},\infty \right)$ i $x\ne 0$.

RejAATNfsMb9C

Ilustracja przedstawia wykres wielomianu. Na rysunku znajduje się układ współrzędnych z poziomą osią X od -1,25 do 0,75 z podziałką co 0,25 oraz z pionową osią Y od -0,75 do 1 z taką samą podziałką. Na płaszczyźnie narysowano wykres wielomianu biegnący niemal pionowo od minus nieskończoności w trzeciej ćwiartce, wykres przecina oś w punkcie x równa się minus jeden, w drugiej ćwiartce przypomina parabolę, dalej przebiega przez początek układu współrzędnych do czwartej ćwiartki, w której biegnie łukiem wybrzuszonym w dół i znowu przecina oś X, tu w punkcie 0,25 i dalej biegnie w pierwszej ćwiartce niemal pionowo do plus nieskończoności. Wszystkie punkty przecięcia wykresu z osią X zaznaczono zamalowanymi punktami. Na osi X zaznaczono następujące przedziały: domknięty od minus jeden do zera oraz lewostronnie domknięty od 0,25 do plus nieskończoności.

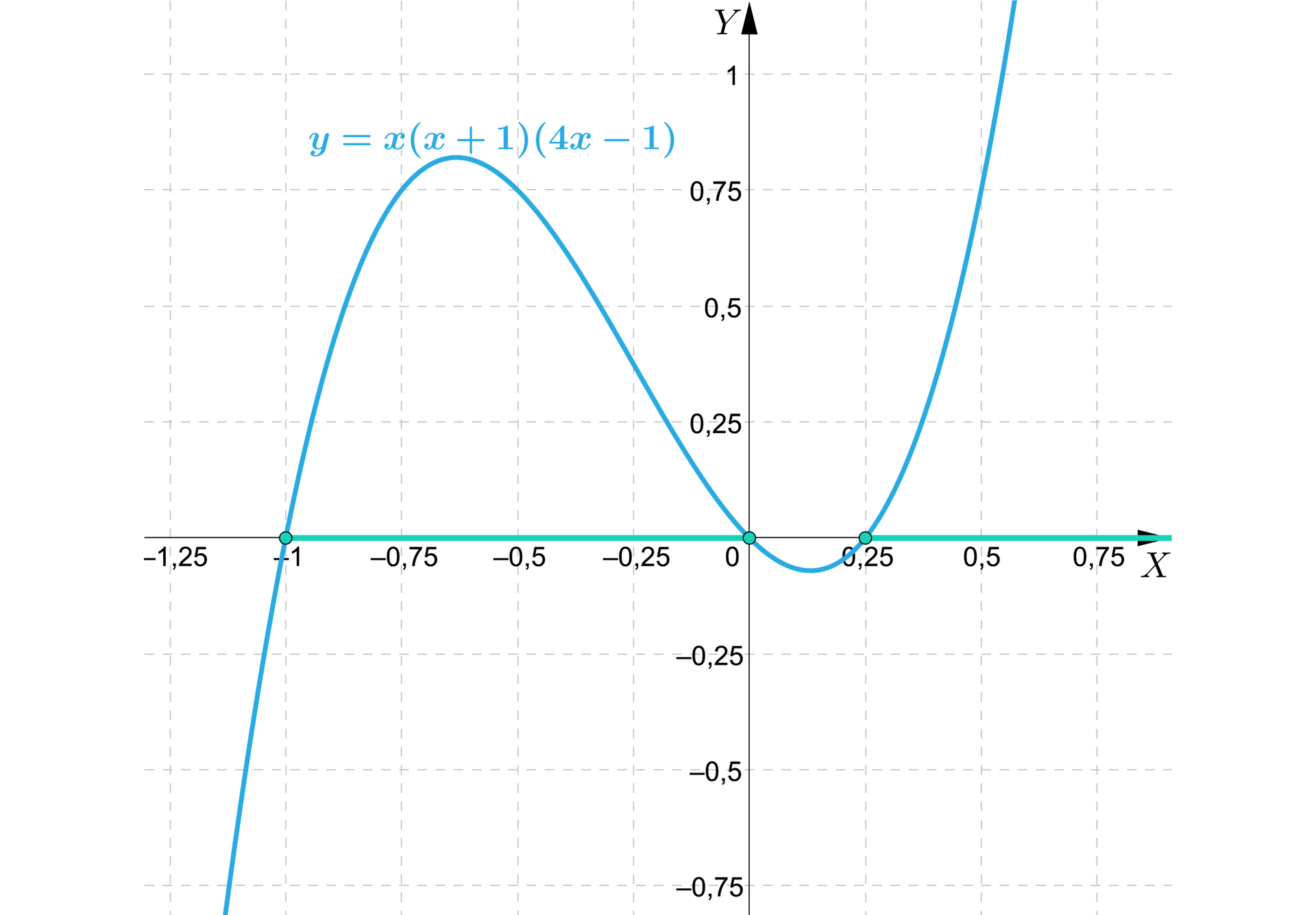
Po uwzględnieniu dziedziny otrzymujemy rozwiązanie nierówności:

$⟨-1,0)\cup (2,\mathrm{\infty })$.

• jeżeli $\left|q\right|<1$ lub $a_1=0$, to szereg geometryczny $\sum _{n=1}^{\infty }{a}_1·q^{n-1}$ jest zbieżny

• jeżeli $a_1=0$, to $\sum _{n=1}^{\infty }{a}_1·q^{n-1}=0$

• jeżeli $\left|q\right|<1$, to $\sum _{n=1}^{\infty }{a}_1·q^{n-1}=\underset{n\to \infty }{\lim }{S}_n=\frac{a_1}{1-q}$