Wykaż, że trójkąt o bokach $\sqrt{17}$ , $\sqrt{85}$, $\sqrt{68}$ jest prostokątny.

R1K8y0QXQwNn5

Ilustracja przedstawia trójkąt ABC. Przy wierzchołku C znajduję się kąt prosty.

Rozwiązanie:

Oznaczmy boki trójkąta $ABC$:

$a=\sqrt{17}$, $b=\sqrt{85}$, $c=\sqrt{68}$.

Korzystamy z twierdzenia odwrotnego do twierdzenia Pitagorasa. Sprawdzamy, czy kwadrat długości jednego z boków jest równy sumie kwadratów długości boków pozostałych. Ponieważ w trójkącie prostokątnym najdłuższym bokiem jest przeciwprostokątna – w naszym przypadku może to być bok o długości $b=\sqrt{85}$. Ograniczymy się zatem tylko do sprawdzenia warunku: $a^2+c^2=b^2$.

Otrzymujemy:

$a^2+c^2={\left(\sqrt{17}\right)}^2+{\left(\sqrt{68}\right)}^2=17+68=85={\left(\sqrt{85}\right)}^2=b^2$.

Wykazaliśmy, że $a^2+c^2=b^2$, więc trójkąt $ABC$ jest prostokątny.

Wykaż, że trójkąt o bokach $\left|AB\right|=7$, $\left|BC\right|=11$, $\left|CA\right|=14$ jest rozwartokątny.

Rozwiązanie:

Trójkąt jest rozwartokątny jeżeli kąt przy jednym z wierzchołków jest rozwarty, czyli $\alpha >{90}^{°}$. Skorzystamy z twierdzenia cosinusów. Sprawdzimy znak funkcji cosinus – jeżeli trójkąt jest rozwartokątny to cosinus kąta rozwartego jest ujemny.

Wprowadźmy oznaczenie: $\sphericalangle ABC=\alpha$.

Zapiszemy twierdzenie cosinusów dla boku $CA$, ponieważ bok leżący naprzeciw kąta o największej mierze jest najdłuższy:

${\left|CA\right|}^2={\left|AB\right|}^2+{\left|BC\right|}^2-2\left|AB\right|\cdot \left|BC\right|\cdot \cos \alpha$.

Wyznaczamy z tego wzoru $\cos \alpha =\frac{{\left|CA\right|}^2-{\left|AB\right|}^2-{\left|BC\right|}^2}{-2\left|AB\right|\cdot \left|BC\right|}$.

Podstawiamy $\left|AB\right|=7$, $\left|BC\right|=11$, $\left|CA\right|=14$:

$\cos \alpha =\frac{{14}^2-7^2-{11}^2}{-2·7·11}=-\frac{26}{154}=-\frac{13}{77}<0$.

Ponieważ $\cos \alpha <0$, to kąt $ABC$ jest rozwarty ( cosinus jest ujemny w $\mathrm{II}$ i $\mathrm{III}$ ćwiartce, $\alpha$ może być tylko kątem z $\mathrm{II}$ ćwiartki układy współrzędnych ponieważ jest kątem trójkąta).

Wykazaliśmy, że trójkąt jest rozwartokątny. Kąt rozwarty znajduje się przy wierzchołku $B$ trójkąta $ABC$.

Trójkąt $ABC$ jest trójkątem prostokątnym o kącie prostym przy wierzchołku $C$. Na przedłużeniu przeciwprostokątnej $AB$ odmierzymy odcinek $BD$ równy przyprostokątnej $BC$ i łączymy punkt $D$ z punktem $C$. Wykaż, że gdy $\left|BC\right|=5$, a $\left|AC\right|=12$, to długość odcinka $CD$ wynosi $\frac{30}{13}·\sqrt{13}$.

R1c3PENZSKGxC

Ilustracja przedstawia trójkąt ACD. Na przedłużeniu boków AC i wierzchołka D powstaje punkt E. Tworząc trójkąt prostokątny AED. Z wierzchołka C prostopadle poprowadzono prostą do ramienia AD tworząc punkt B. Ramię CD ma wartość x.

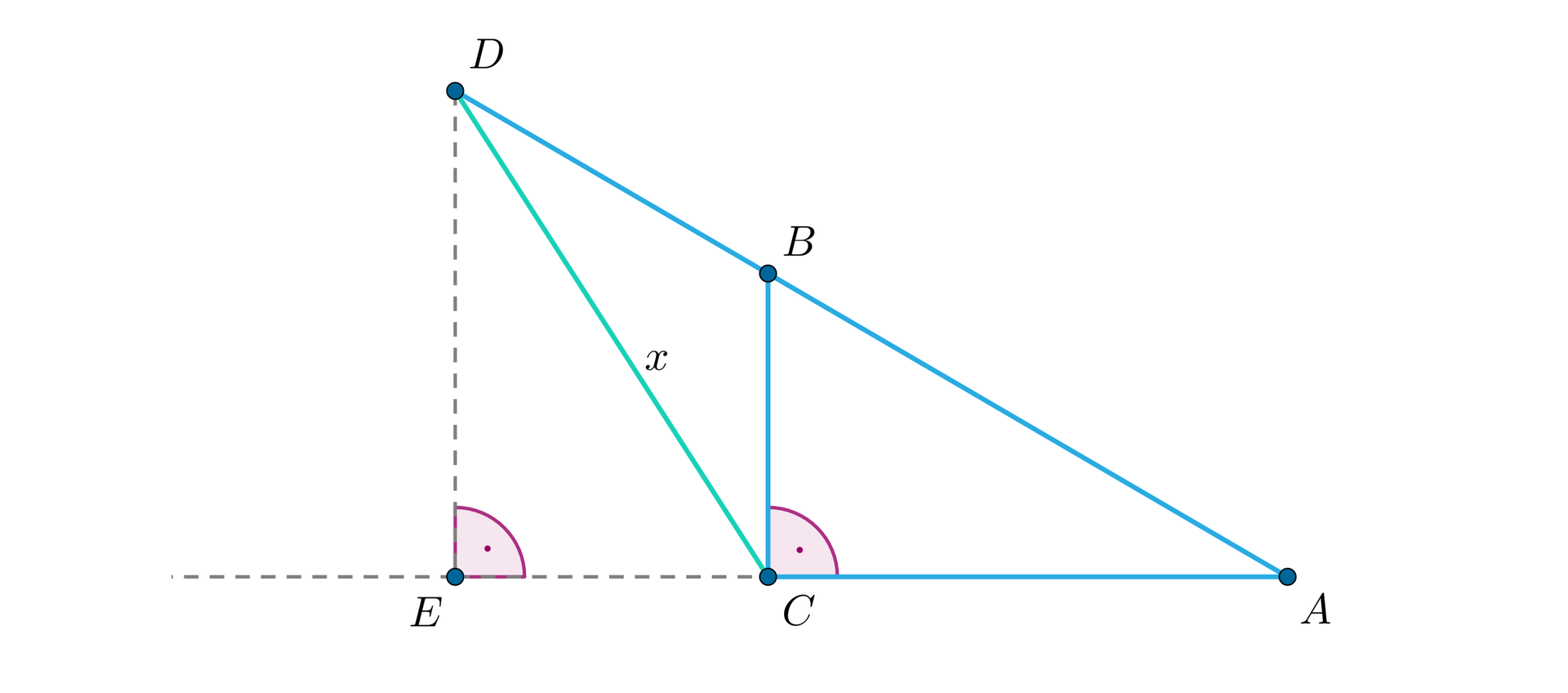
Rozwiązanie:

$\text{I}$ metoda:

Pomocniczo wprowadzamy odcinki $DE$ i $EC$, $DE\parallel CB$. Z treści zadania wiemy, że $\left|AC\right|=12$, $\left|CB\right|=5$, $\left|DB\right|=5$.

Rozwiązanie znajdziemy wykonując następujące kroki:

1. Z twierdzenia Pitagorasa dla trójkąta prostokątnego $ABC$ wyznaczymy $AB$.

2. Z twierdzenia Talesa wyznaczymy $DE$ i $EC$.

3. Z twierdzenia Pitagorasa dla trójkąta prostokątnego $DEC$ wyznaczymy $\left|CD\right|=x$.

Trójkąt $ABC$ jest prostokątny, zatem z twierdzenia Pitagorasa, możemy zapisać: ${\left|AC\right|}^2+{\left|CB\right|}^2={\left|AB\right|}^2$.

Ponieważ $\left|AB\right|=\sqrt{{\left|AC\right|}^2+{\left|CB\right|}^2}$, $\left|AC\right|=12$, $\left|CB\right|=5$, zatem:

$\left|AB\right|=\sqrt{{12}^2+5^2}=\sqrt{169}=13$.

$\left|AB\right|=13$.

Ponieważ $DE\Vert CB$, to z twierdzenia Talesa możemy zapisać:

1) $\frac{\left|DE\right|}{\left|CB\right|}=\frac{\left|AD\right|}{\left|AB\right|}$

$\left|AD\right|=\left|DB\right|+\left|AB\right|$ (co wynika z treści zadania).

$\left|AD\right|=5+13=18$, $\left|CB\right|=5$, $\left|AB\right|=13$.

Otrzymujemy:

$\frac{\left|DE\right|}{5}=\frac{18}{13}$, skąd $\left|DE\right|=\frac{5·18}{13}$.

2) $\frac{\left|EC\right|}{\left|AC\right|}=\frac{\left|DB\right|}{\left|AB\right|}$

Wiemy, że $\left|AC\right|=12$, $\left|DB\right|=5$, $\left|AB\right|=13$

Otrzymujemy:

$\frac{\left|EC\right|}{12}=\frac{5}{13}$, skąd $\left|EC\right|=\frac{12·5}{13}$.

$\left|CD\right|=x$ wyznaczymy z twierdzenia Pitagorasa zapisanego dla trójkąta $CDE$:

$x^2={\left|CD\right|}^2={\left|DE\right|}^2+{\left|EC\right|}^2$.

$x^2={\left(\frac{5\cdot 18}{13}\right)}^2+{\left(\frac{12\cdot 5}{13}\right)}^2={\left(\frac{5}{13}\right)}^2\left({18}^2+{12}^2\right)={\left(\frac{5}{13}\right)}^2\left({\left(3\cdot 6\right)}^2+{\left(2\cdot 6\right)}^2\right)=$$={\left(\frac{5}{13}\right)}^2·6^2·\left(3^2+2^2\right)={\left(\frac{5·6}{13}\right)}^2·13$.

Stąd $\left|CD\right|=\frac{30}{13}·\sqrt{13}$.

$\text{II}$ metoda:

R1bf6LCjT7cl8

Ilustracja przedstawia trójkąt ACD. Z wierzchołka C prostopadle poprowadzono prostą do ramienia AD tworząc punkt B. Ramię CD ma wartość x. Utworzono dwa trójkąty wewnętrzne. BCD o kącie przy wierzchołku B o wartości beta oraz trójkąt ABC o kącie przy wierzchołku B o wartości alfa.

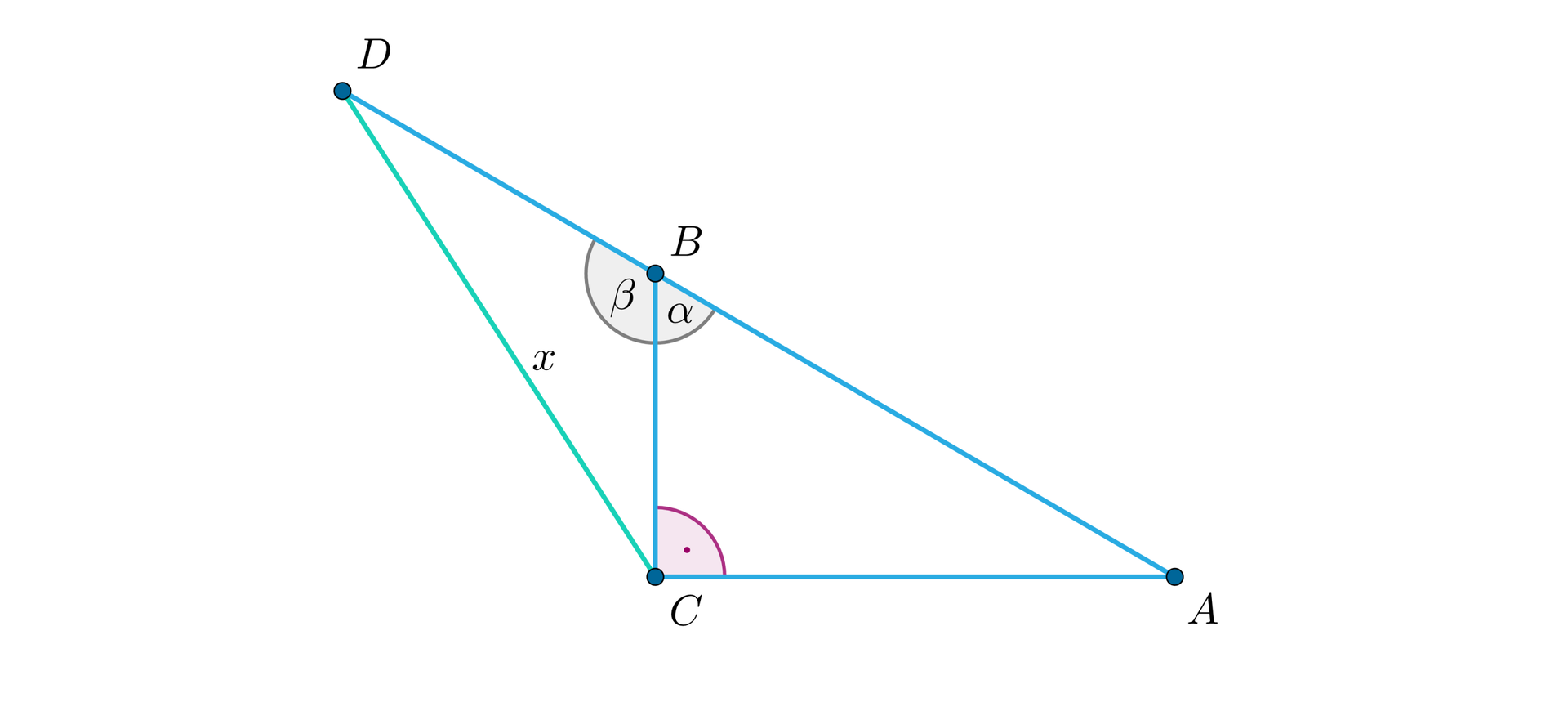
Ponieważ trójkąt $ABC$ jest prostokątny, to z twierdzenia Pitagorasa możemy zapisać:${\left|AC\right|}^2+{\left|CB\right|}^2={\left|AB\right|}^2$.

Wiemy, że $\left|AB\right|=\sqrt{{\left|AC\right|}^2+{\left|CB\right|}^2}$, $\left|AC\right|=12$, $\left|CB\right|=5$, więc $\left|AB\right|=\sqrt{{12}^2+5^2}=\sqrt{169}=13$.

Otrzymujemy zatem $\left|AB\right|=13$

Oznaczmy: $\sphericalangle CBA=\alpha$ i $\sphericalangle DBC=\beta$.

Ponieważ $\alpha$, $\beta$ to kąty przyległe, to $\alpha +\beta =180°$, a stąd $\beta =180°-\alpha$.

Trójkąt $ABC$ jest prostokątny, możemy zatem zapisać : $\cos \alpha =\frac{\left|BC\right|}{\left|AB\right|}$.

$\left|BC\right|=5$, $\left|AB\right|=13$, a zatem $\cos \alpha =\frac{\left|BC\right|}{\left|AB\right|}=\frac{5}{13}$.

Ponieważ $\beta =180°-\alpha \to \cos \beta =\cos \left(180°-\alpha \right)=-\cos \alpha$ (ze wzoru redukcyjnego). Otrzymujemy zatem $\cos \beta =-\left(\frac{5}{13}\right)$.

Z twierdzenia cosinusówtwierdzenie cosinusówtwierdzenia cosinusów dla trójkąta $CDB$ zapisujemy: ${\left|CD\right|}^2={\left|CB\right|}^2+{\left|DB\right|}^2-2·\left|CB\right|·\left|DB\right|·\cos \beta$.

$x=\left|CD\right|$.

$x^2=5^2+5^2-2·5·5·\left(\frac{-5}{13}\right)=25+25+\frac{250}{13}=$$=25\left(2+\frac{10}{13}\right)=5^2·\frac{36}{13}=5^2·\frac{6^2}{13}$.

Ponieważ $x^2=5^2·\frac{6^2}{13}$, stąd też $x=\sqrt{5^2·\frac{6^2}{13}}=\frac{30}{\sqrt{13}}=\frac{30}{13}\sqrt{13}$.

Wykazaliśmy, że $\left|CD\right|=\frac{30}{13}·\sqrt{13}$.

Wykaż, że jeżeli trójkąt ma dwie równe wysokości to jest równoramienny.

R6DpgKHbIsMMa

Ilustracja przedstawia trójkąt ABC. Z wierzchołka B prostopadle do ramienia AC poprowadzono prostą tworząc punkt D. Z wierzchołka C prostopadle poprowadzono prostą na ramie AB tworząc punkt E.

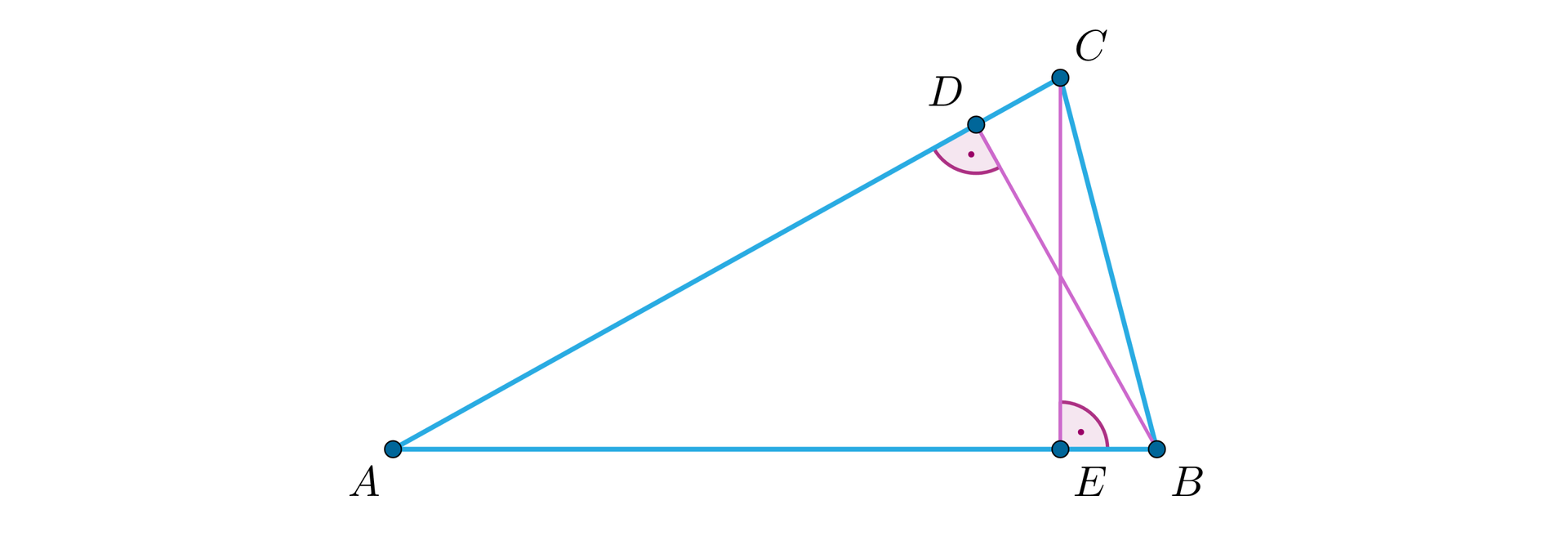
Rozwiązanie:

Niech $CE$ i $DB$ będą wysokościami $\Delta ABC$ i $CE=DB$.

Rozważmy trójkąty $ABD$ i $AEC$.

$\sphericalangle CAB$ kąt wspólny trójkątów: $ABD$ i $AEC$.

$\sphericalangle ADB=\sphericalangle AEC=90°$ ponieważ $DB$ i $CE$ są wysokościami trójkąta.

$\sphericalangle DBA=\sphericalangle ACE$, ponieważ jeżeli dwa trójkąty prostokątne mają jeden kąt ostry równy, to również drugi kąt ostry jest tej samej miary.

Z założenia mamy zatem $CE=DB$.

Z cechy ($kbk$) trójkąty są przystające więc $AC=AB$. Zatem trójkąt $ABC$ jest równoramienny.

jeżeli $a$, $b$, $c$ są długościami boków trójkąta, natomiast $\alpha$, $\beta$, $\gamma$ odpowiednio miarami kątów leżących naprzeciw tych boków, to:
$c^2=a^2+b^2-2ab\cos \gamma$
$a^2=b^2+c^2-2bc\cos \alpha$
$b^2=a^2+c^2-2ac\cos \beta$