Przeczytaj
Linia środkowa w trójkącie jest to odcinek łączący środki dwóch boków trójkąta.
W każdym trójkącie istnieją trzy różne linie środkowe, każdej z nich odpowiada jeden bok trójkąta – ten, który nie został wybrany do wyznaczenia linii środkowej.
Bok odpowiadający danej linii środkowej będziemy nazywali podstawą.
Trójkąt, którego boki są liniami środkowymi będziemy nazywali trójkątem środkowymtrójkątem środkowym.
Na rysunku różnymi kolorami zaznaczone są pary: linia środkowalinia środkowa i odpowiadająca jej podstawa.
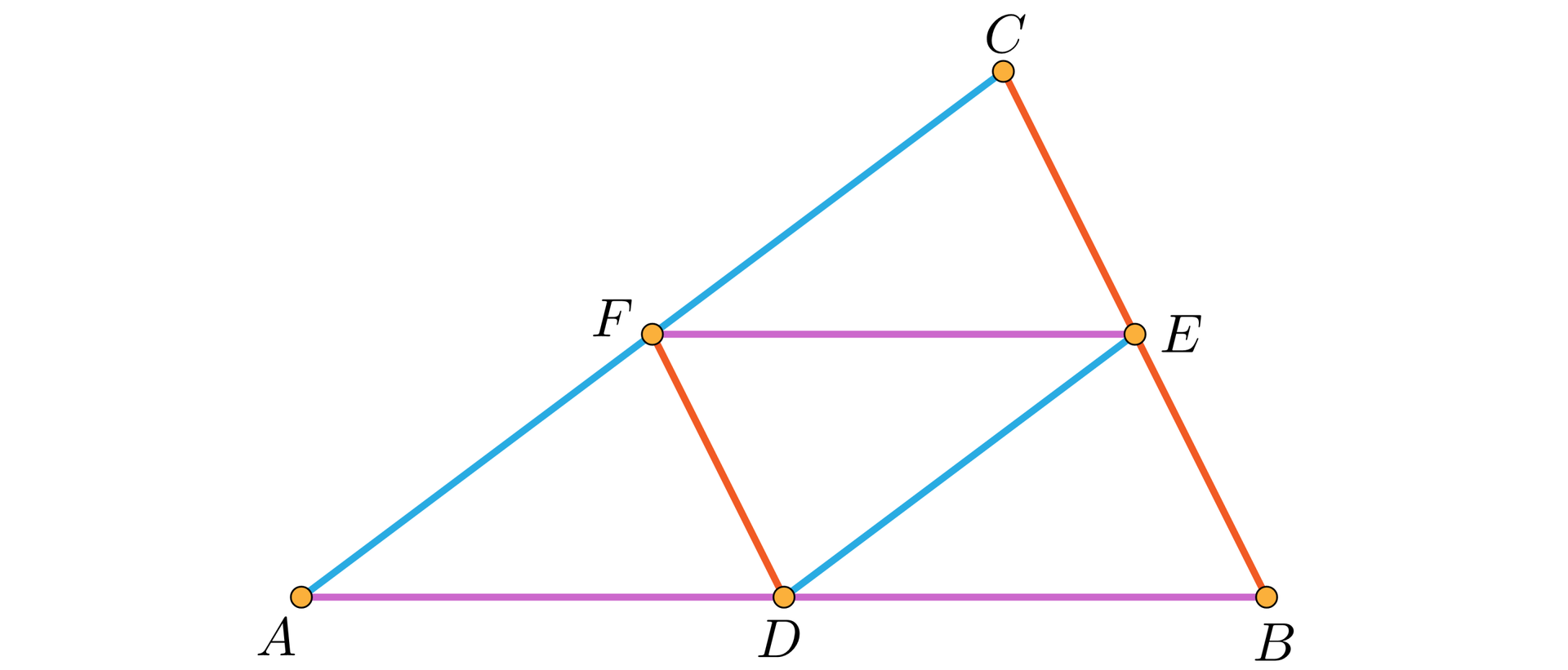
Trójkąt jest trójkątem środkowym.
Linia środkowa w trójkącie jest równoległa do podstawy i długość linii środkowej jest równa połowie długości podstawy.
Zobaczmy film, który pozwoli nam utrwalić twierdzenie o linii środkowej w trójkącie. Poznamy też dowód wykorzystujący wektory.
Film dostępny pod adresem https://zpe.gov.pl/a/DoGjgiVzP
Film nawiązujący do treści materiału dotyczącej twierdzenia o linii środkowej w trójkącie.
Wnioski z twierdzenia o linii środkowej w trójkącie
Trójkąty wyznaczone przez linie środkowe w trójkącie są podobne do tego trójkąta w skali .
Linie środkowe w trójkącie dzielą ten trójkąt na trójkąty przystające, czyli trójkąty przystające do trójkąta środkowego.
Pole każdego z czterech przystających trójkątów wyznaczonych przez linie środkowe jest razy mniejsze od pola trójkąta wyjściowego.
Obliczymy długości linii środkowych w trójkącie o bokach długości , , .
Rozwiązanie
Bezpośrednio z powyższego twierdzenia wynika, że środkowa odpowiadająca postawie ma długość , środkowa linia odpowiadająca podstawie ma długość a środkowa linia odpowiadająca podstawie ma długość .
Przy oznaczeniach z poniższego rysunku pokażemy, że:
czworokąt jest trapezemtrapezem
czworokąt jest równoległobokiemrównoległobokiem
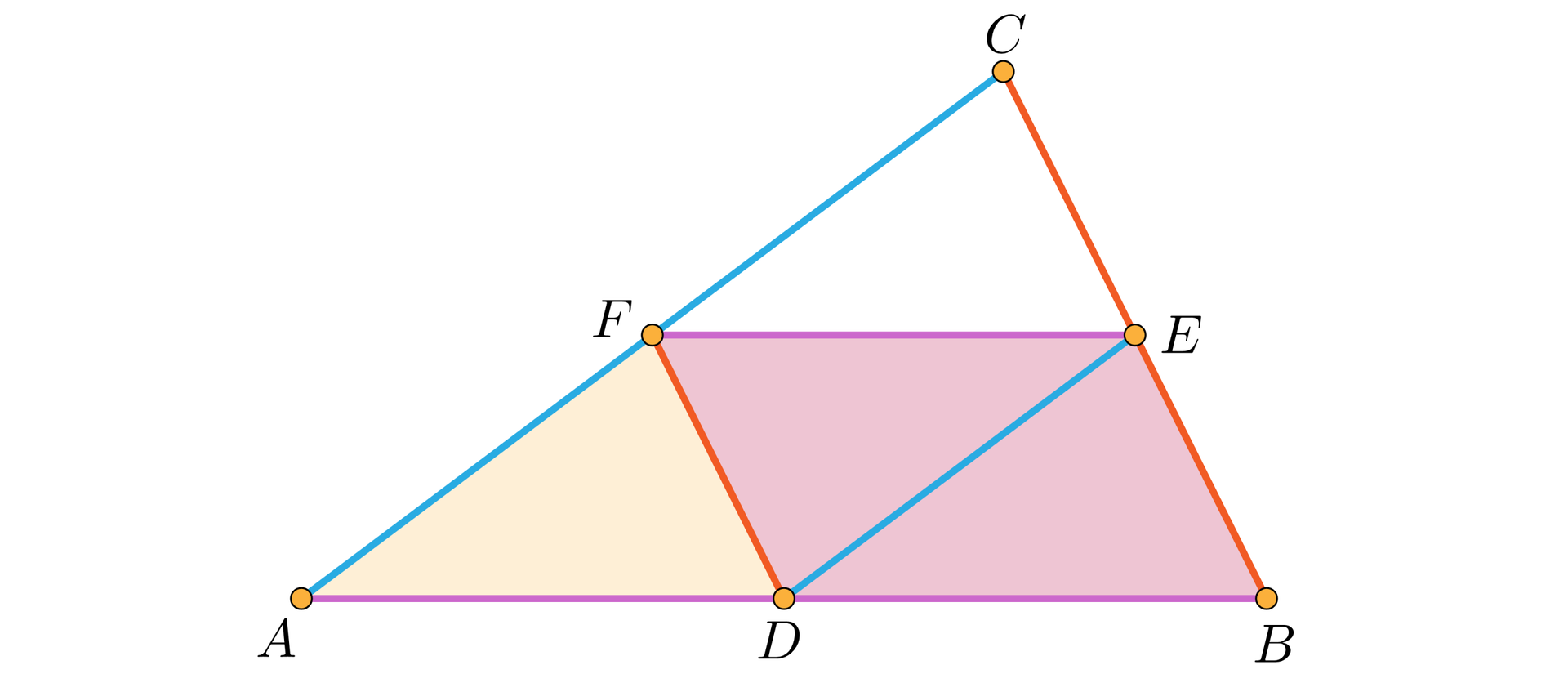
Rozwiązanie
Wprost z twierdzenia o linii środkowej w trójkącie , więc czworokąt jest trapezem a czworokąt jest równoległobokiem. Również z tego twierdzenia wynika, że i .
Jakie jeszcze trapezy i równoległoboki widać na rysunku?
Załóżmy, że pole trójkąta środkowego w trójkącie jest równe . Wyznaczymy pole trójkąta oraz pola trapezów i równoległoboków powstałych po narysowaniu linii środkowych w trójkącie .
Rozwiązanie
Na rysunku przedstawiony jest trójkąt , trójkąt środkowy i trzy trójkąty przystające do trójkąta środkowego. Obliczymy pola figur.
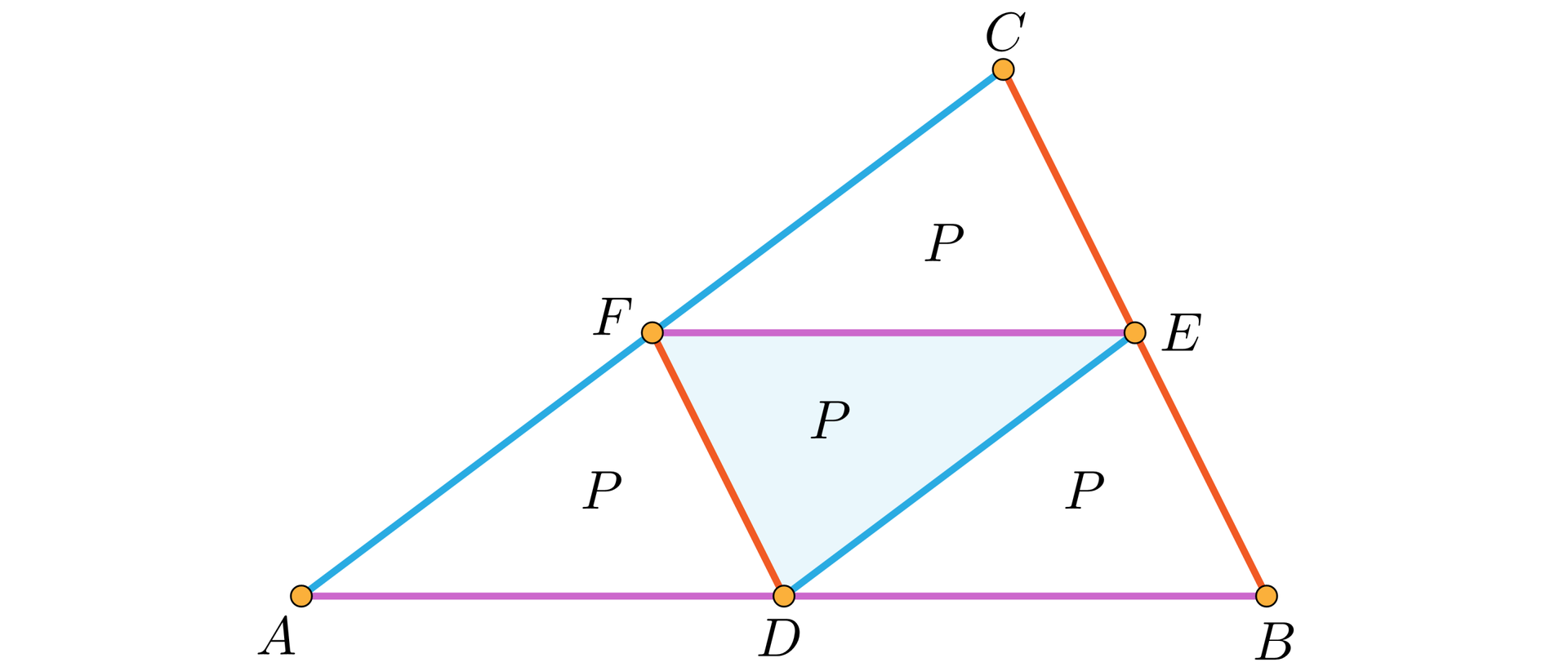
Ponieważ te trójkąty są przystające, to pole każdego z nich jest równe .
Pole trójkąta jest równe .
Pola trapezów , i są równe i wynoszą .
Pola równoległoboków , i są równe i wynoszą .
Jeżeli odcinek łączący dwa boki trójkąta jest równoległy do trzeciego boku i ma długość równą połowie długości trzeciego boku, to odcinek ten jest linią środkową w trójkącie.
Popatrzmy na rysunek. Załóżmy, że i .
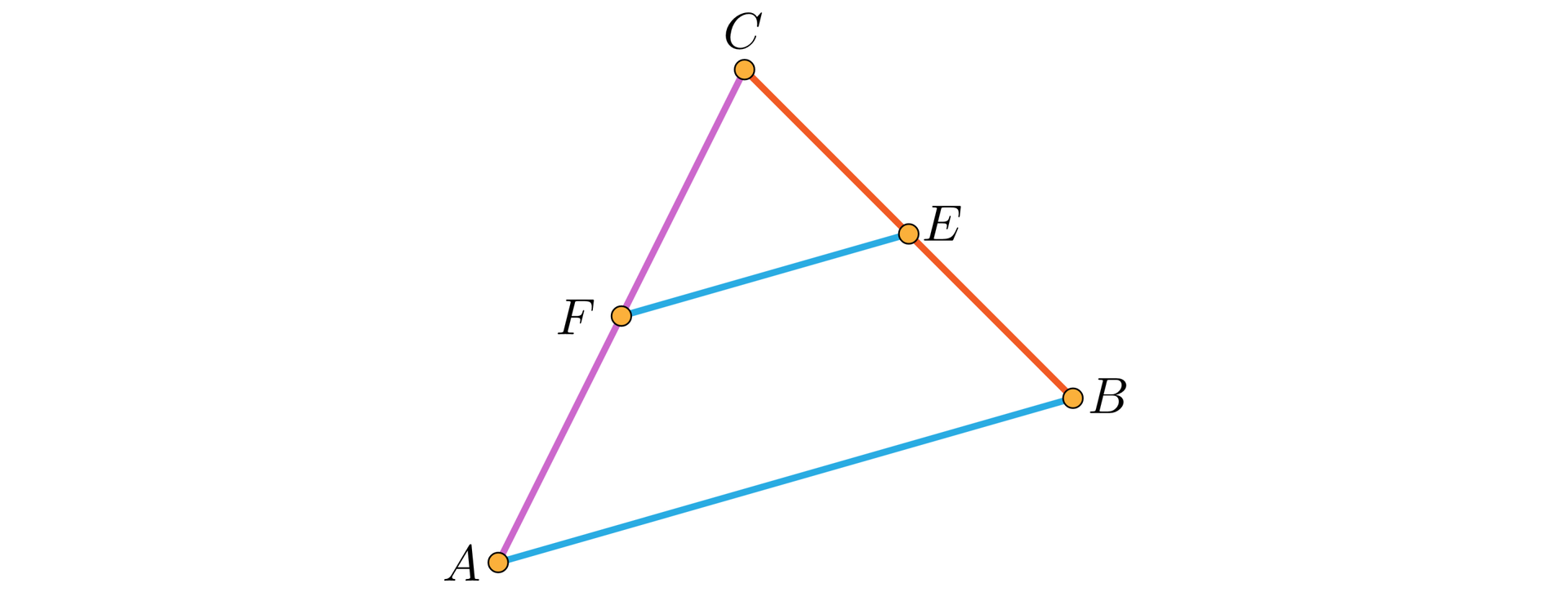
Wtedy z wniosków z twierdzenia Talesa wynika, że , a stąd punkt jest środkiem odcinka . Podobnie pokazuje się, że punkt jest środkiem odcinka .
Nie należy mylić linii środkowej w trójkącie z pojęciem środkowej, gdyż środkowa w trójkącieśrodkowa w trójkącie jest to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.
Aby lepiej zapamiętać tę różnice w definicjach środkowej i linii środkowej udowodnimy następujące twierdzenie:
Środkowe w trójkącie przecinają się w jednym punkcie i punkt ten dzieli środkowe w stosunku licząc od wierzchołków trójkąta.
Na rysunku przedstawiono dwie środkowe i . Wtedy jest linią środkową w trójkącie .
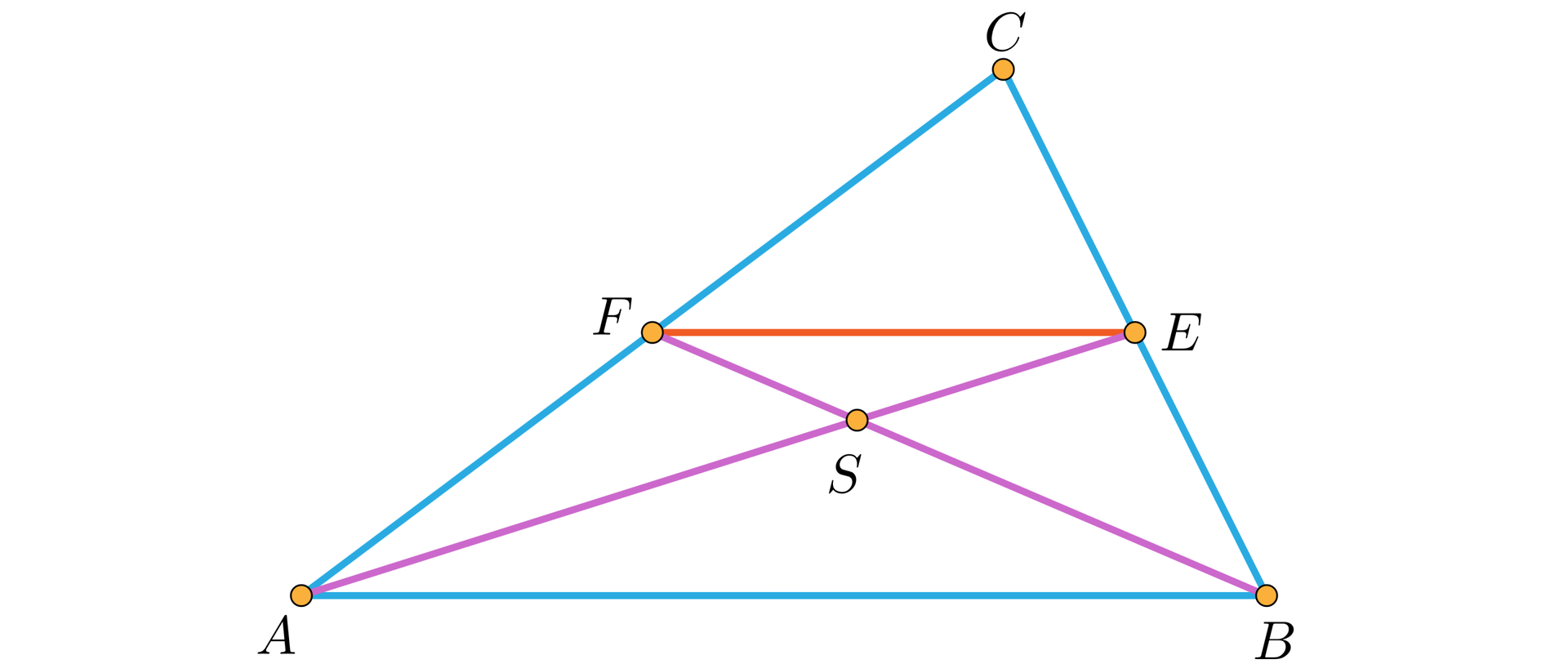
Z twierdzenia o linii środkowej w trójkącie wynika, że
i .
Stąd, na mocy uogólnienia twierdzenia Talesa trójkąty i są podobne i
Teraz trzeba pokazać, że trzecia środkowa poprowadzona w wierzchołka przechodzi przez punkt oraz, że punkt dzieli tę środkową w stosunku .
Niech punkt będzie środkiem boku i niech oznacza punkt przecięcia środkowej i środkowej . Ponieważ argumentacja przedstawiona wyżej nie zależała od wyboru środkowych, to punkt dzieli środkowe i w stosunku . Stąd zarówno punkt jak i punkt dzielą odcinek w stosunku , a to jest możliwe tylko wtedy, gdy .
Pokażemy, że wysokości trójkąta równobocznego przecinają się w stosunku .
Rozwiązanie
Zauważmy, że w trójkącie równobocznym wysokości są jednocześnie środkowymi trójkąta, więc na mocy twierdzenia o punkcie przecięcia środkowych w trójkącie wysokości trójkąta równobocznego przecinają się w stosunku .
Wysokość trójkąta równoramiennego poprowadzona do podstawy i linia środkowa łącząca środek podstawy ze środkiem ramienia mają długość .
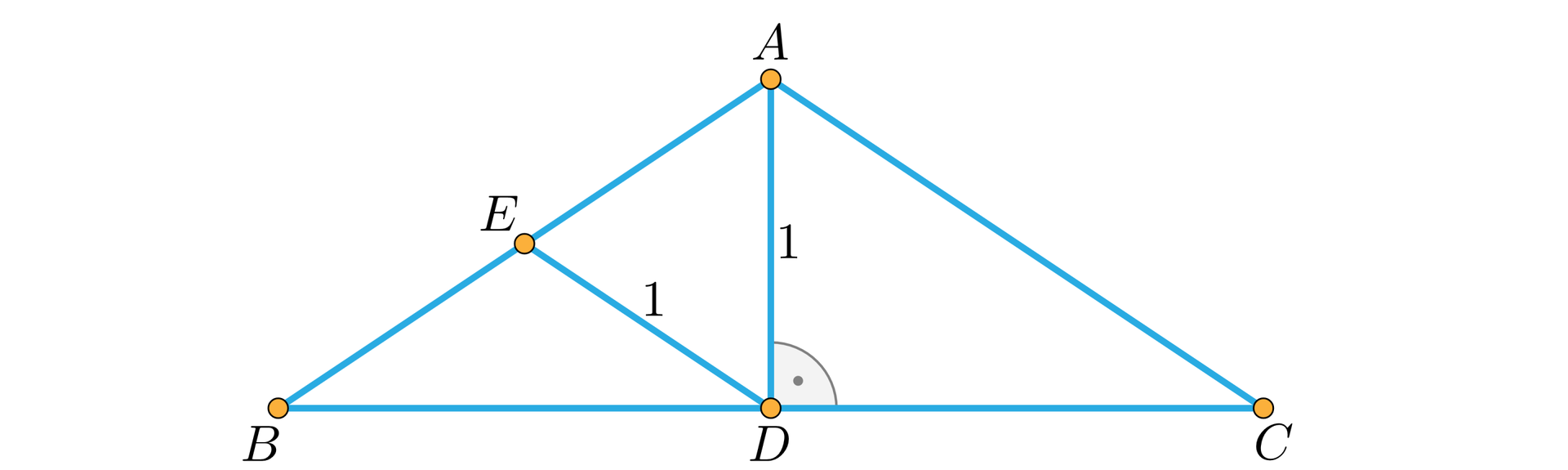
Obliczymy długość podstawy tego trójkąta.
Rozwiązanie
Z twierdzenia o linii środkowej w trójkącie . Z twierdzenia Pitagorasa . Stąd .
Zatem podstawa ma długość .
Słownik
odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku
trójkąt, którego boki są liniami środkowymi w danym trójkącie
odcinek łączący środki dwóch boków trójkąta
czworokąt, który ma co najmniej jedną parę boków równoległych
czworokąt, który ma dwie pary boków równoległych