Przeczytaj
Przypomnijmy podstawowe definicje i własności ostrosłupów.
Ostrosłup czworokątny to ostrosłup, który ma w podstawie czworokąt. Ostrosłup czworokątny prosty to ostrosłup czworokątny, w którym spodek wysokości pokrywa się ze środkiem okręgu opisanego na podstawie ostrosłupa. Ostrosłup prawidłowy czworokątny to ostrosłup prosty, którego podstawą jest kwadrat. Możemy podać również równoważną definicję ostrosłupa prawidłowego czworokątnego, nie odwołując się do pojęcia ostrosłupa prostego: ,,ostrosłup prawidłowy czworokątny to ostrosłup, w którego podstawie jest kwadrat, a wszystkie ściany boczne są przystającymi trójkątami równoramiennymi”.
Wzór na objętość ostrosłupa:
gdzie:
– pole podstawy,
– wysokość ostrosłupa.
Podstawą ostrosłupa prostego jest trapez równoramienny o podstawach i oraz kącie ostrym . Krawędzie boczne są nachylone do płaszczyzny podstawy pod tym samym kątem . Obliczymy objętość tego ostrosłupa.
Rozwiązanie:
Wykonajmy rysunek pomocniczy i wprowadźmy dodatkowe oznaczenia. Niech – długość ramion trapezu, – wysokość trapezu, – długość przekątnej trapezu, – wysokość ostrosłupa.
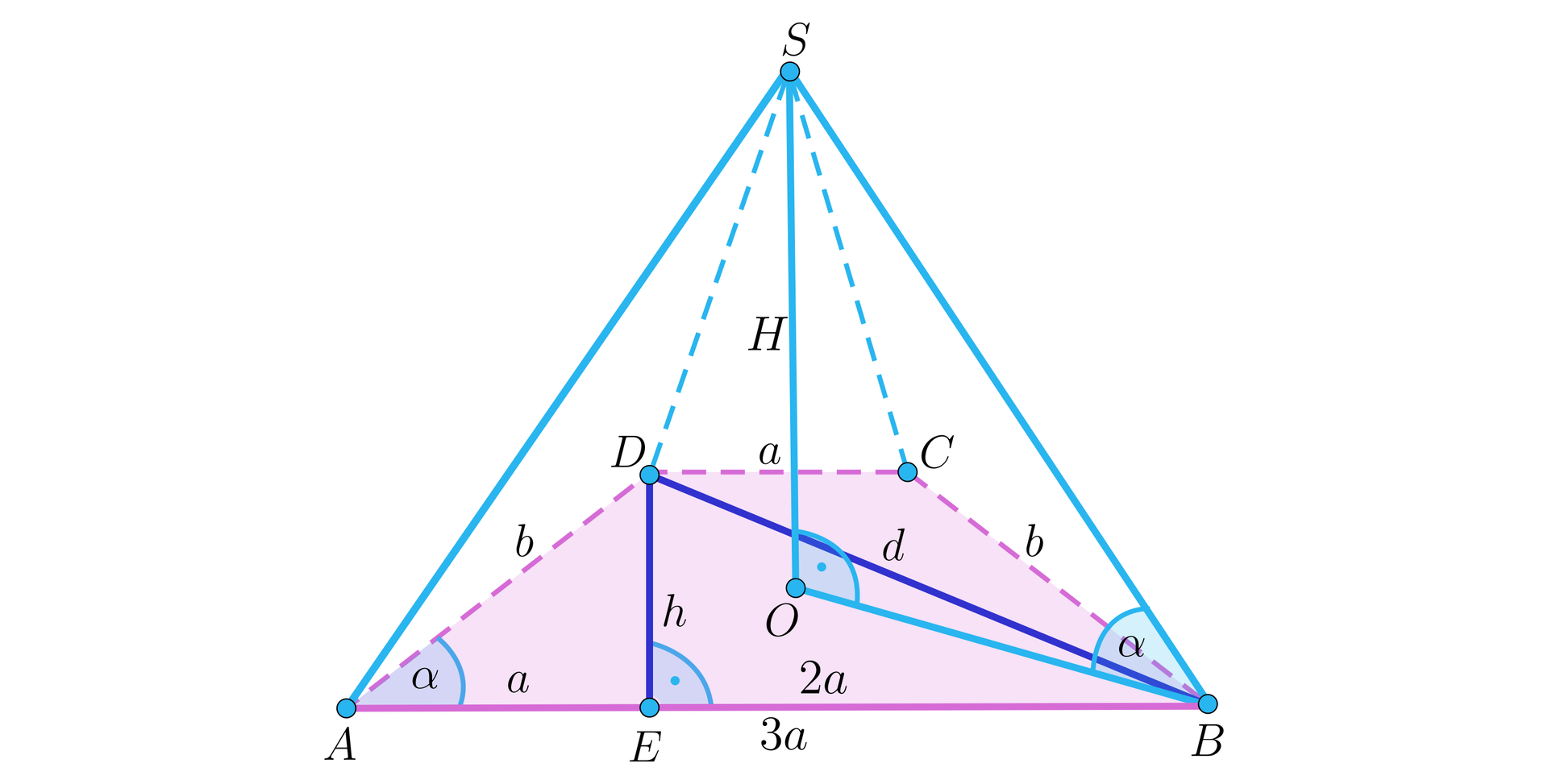
Trójkąt jest prostokątny, więc wykorzystując funkcje trygonometryczne mamy:
, więc .
Mamy już wszystkie informacje, by policzyć pole podstawy ostrosłupa. Aby obliczyć wysokość ostrosłupa, musimy mieć długość odcinka . Ostrosłup jest prostyOstrosłup jest prosty, zatem jest to promień okręgu opisanego na jego podstawie. Obliczmy więc jego długość. Wystarczy obliczyć długość promienia okręgu opisanego na trójkącie . W tym celu wyznaczymy pole trójkąta korzystając z dwóch różnych wzorów.
Wzór wykrzystujący promień okręgu opisanego na trójkącie wymaga znajomości długości wszystkich boków trójkąta. Musimy więc wyznaczyć wielkości i .
Ponieważ , więc ,
Trójkąt jest także prostokątny, co pozwoli nam na obliczenie przekątnej trapezu:
.
Policzmy pole trójkąta:
.
Zatem obliczmy promień. Oznaczmy go jako :
.
Trójkąt jest prostokątny. Zatem:
, , więc
.
Obliczmy pole podstawy ostrosłupa:
.
Objętość ostrosłupa wynosi więc:
.
Rozważmy wszystkie ostrosłupy prawidłowe czworokątneostrosłupy prawidłowe czworokątne, w których suma promienia okręgu opisanego na podstawie ostrosłupa i wysokości tego ostrosłupa jest równa . Wyznaczymy promień okręgu opisanego na podstawie tego z ostrosłupów, który ma największą objętość. Obliczymy tę objętość.
Rozwiązanie:
Zauważmy, że jest to zadanie optymalizacyjne.
Oznaczmy bok kwadratu jako , wysokość ostrosłupa – .
Promień okręgu opisanego na podstawie ma wzór .
Z treści zadania wiemy, że
, . Zatem .
Wyznaczmy wzór na objętość ostrosłupa.
.
Obliczmy pochodną naszej funkcji .
Znajdźmy ekstrema funkcji .
Zatem
– nie spełnia warunków zadania
lub
.
dla oraz dla , więc jest maksimum lokalnym
Największa objętość ostrosłupa będzie więc dla . Promień okręgu opisanego na podstawie tego ostrosłupa to
Największa objętość ostrosłupa to:
.
Podstawą ostrosłupa jest romb o boku i kącie ostrym . Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem . Obliczymy objętość ostrosłupa.
Rozwiązanie:
Wykonajmy rysunek pomocniczy:

Skoro kąt ostry naszego rombu ma miarę to znaczy, że wysokość rombu ma długość .
Zatem .
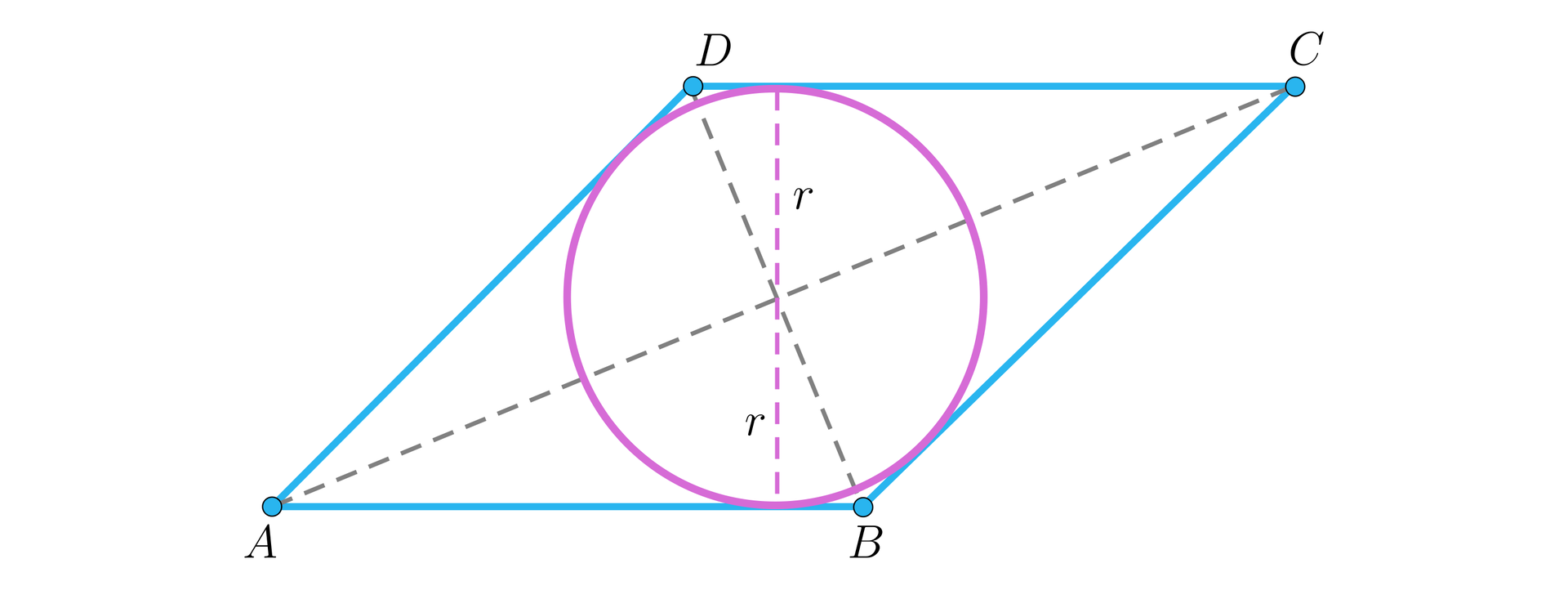
Promień okręgu wpisanego w romb jest równy połowie jego wysokości, zatem .
Ściany boczne są nachylone do płaszczyzny podstawy pod kątem .
Trójkąt jest prostokątny, co w łatwy sposób pozwoli nam policzyć wysokość ostrosłupa.
.
Możemy już liczyć objętość ostrosłupa:
.
Na rysunku przedstawiono siatkę ostrosłupa, w którego podstawie jest kwadrat. Wysokością ostrosłupa jest jedna z jego krawędzi bocznych. Objętość ostrosłupa wynosi .
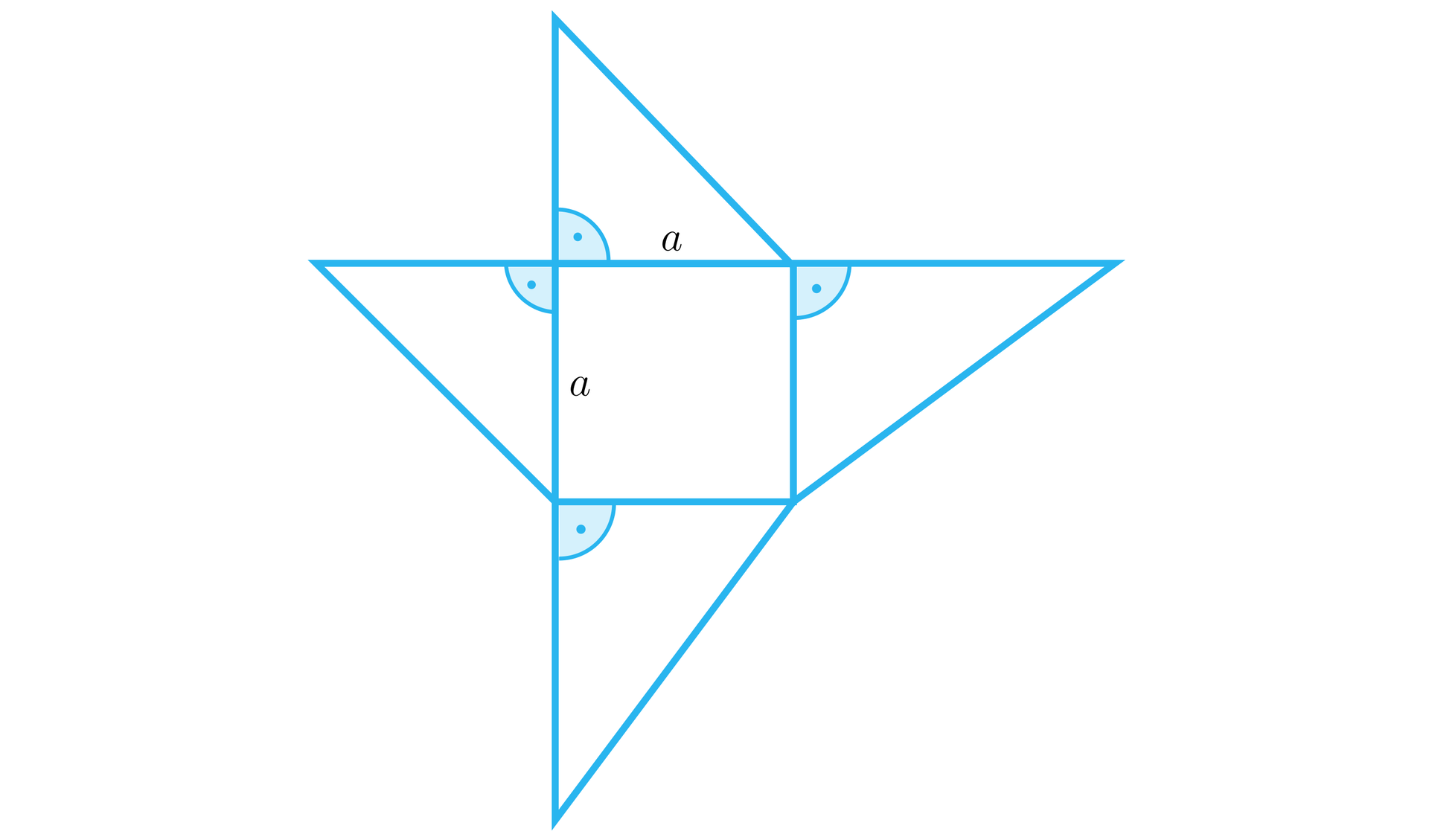
Obliczymy miarę kąta nachylenia najdłuższej krawędzi bocznej do krawędzi podstawy.
Rozwiązanie:
Oznaczmy wysokość ostrosłupa jako . Wówczas mamy równanie:
.
Narysujmy bryłę naszego ostrosłupa. Oznaczmy kąt nachylenia najdłuższej krawędzi bocznej do krawędzi podstawy jako .

Trójkąt jest prostokątnym trójkątem równoramiennym. Zatem .
Trójkąt także jest prostokątny. , zatem
.
Rozważmy trójkąt . Zauważmy, że
.
Trójkąt jest więc prostokątny, więc:
.
Z tablic wartości trygonometrycznych odczytujemy wartość kąta:
.
Podstawą ostrosłupa jest prostokąt , którego boki mają długość i . Ściany boczne i są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem . Ściany boczne i są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem . Miary kątów i spełniają warunek . Obliczymy objętość ostrosłupa.
Rozwiązanie:
Wykonajmy rysunek pomocniczy:
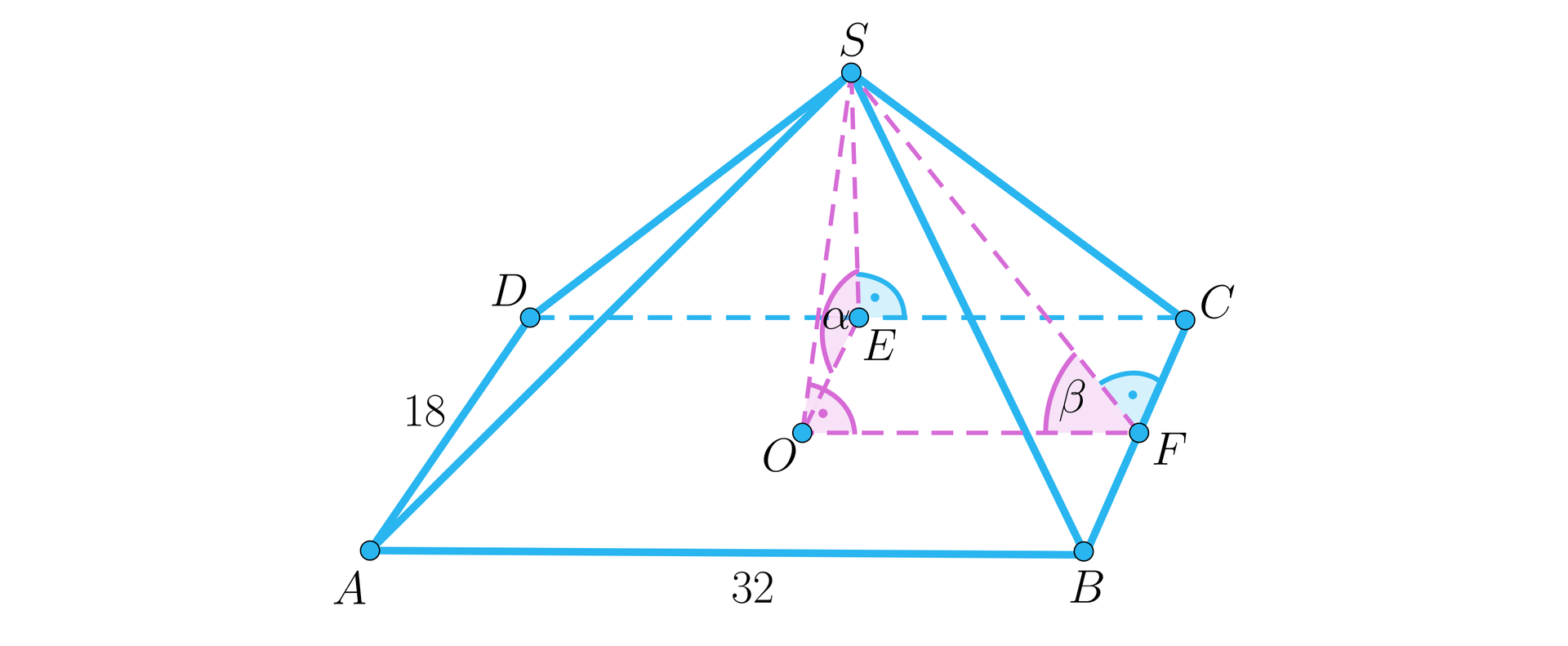
Trójkąty i są prostokątne.
, .
Korzystając z funkcji trygonometrycznych mamy więc:
i .
Z treści zadania wiemy, że , więc .
Zatem mamy, że
.
Możemy więc obliczyć objętość naszego ostrosłupa.
.
Słownik
w podstawie ma czworokąt, spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie
ostrosłup, w którego podstawie jest kwadrat, a wszystkie ściany boczne są przystającymi trójkątami równoramiennymi