Przeczytaj

Kąt wpisany w koło

Definicja: Kąt wpisany w koło

Kątem wpisanym w koło nazywamy kąt wypukły, którego ramionami są proste zawierające cięciwy tego koła, a wierzchołek należy do brzegu koła.

Ra8FDCxr8Cm1k

Rysunek przedstawia koło, w którym wykreślono dwie cięciwy: CA oraz CB i przedłużono je poza pole koła linią przerywaną. Cięciwy tworzą dwa kąty: pierwszy z nich jest zaznaczony tylko w polu koła między cięciwami - to kąt wypukły α oraz kąt wklęsły ograniczony cięciwami zaznaczony w polu koła i poza nim. Kąt ten dopełnia kąt α do trzystu sześćdziesięciu stopni. Kąt wklęsły opisano jako β. — Kąt wpisany

Na powyższym rysunku, dwie półproste: $C A$ i $C B$ , zaznaczone liniami przerywanymi, są ramionami dwóch kątów o wierzchołku w punkcie $C$ : kąta wypukłego $α$ oraz kąta wklęsłego $β$ . Tylko kąt $α$ jest kątem wpisanym w kołokołokoło, bo zgodnie z definicją musi to być kąt wypukły.

Ilustrując zagadnienie kątów wpisanych, będziemy zwykle zaznaczać jedynie promienie danego koła, zawarte w odpowiednich półprostych tak, jak na poniższym rysunku.

R1FGqwCc3BV1G

Rysunek przedstawia koło, w którym wykreślono trzy cięciwy CA, CB oraz AB, które tworzą trójkąt ABC. Przy wierzchołku C zaznaczono kąt α.

W praktyce szkolnej spotykamy się z zamiennym stosowaniem pojęć: kąt wpisany w koło i kąt wpisany w okrąg, dlatego przyjmujemy również kolejną definicję.

Kąt wpisany w okrąg

Definicja: Kąt wpisany w okrąg

Rozważmy okrąg o środku $O$ i punkty $A$ , $B$ leżące na tym okręgu. Kątem wpisanym opartym na łuku $A B$ nazywamy kąt wypukły $A C B$ , którego ramiona zawierają cięciwy okręgucięciwa okręgucięciwy okręgu $C A$ i $C B$ .

R1KikARvwilcG

Rysunek przedstawia okrąg, w którym wykreślono dwie cięciwy: CA oraz CB. Na okręgu zaznaczono łuk między punktami A i B.

Zauważmy, że każdy kąt wpisany danego okręgu w sposób jednoznaczny wyznacza łuk, na którym jest on oparty.

RX07OX3ClhE56

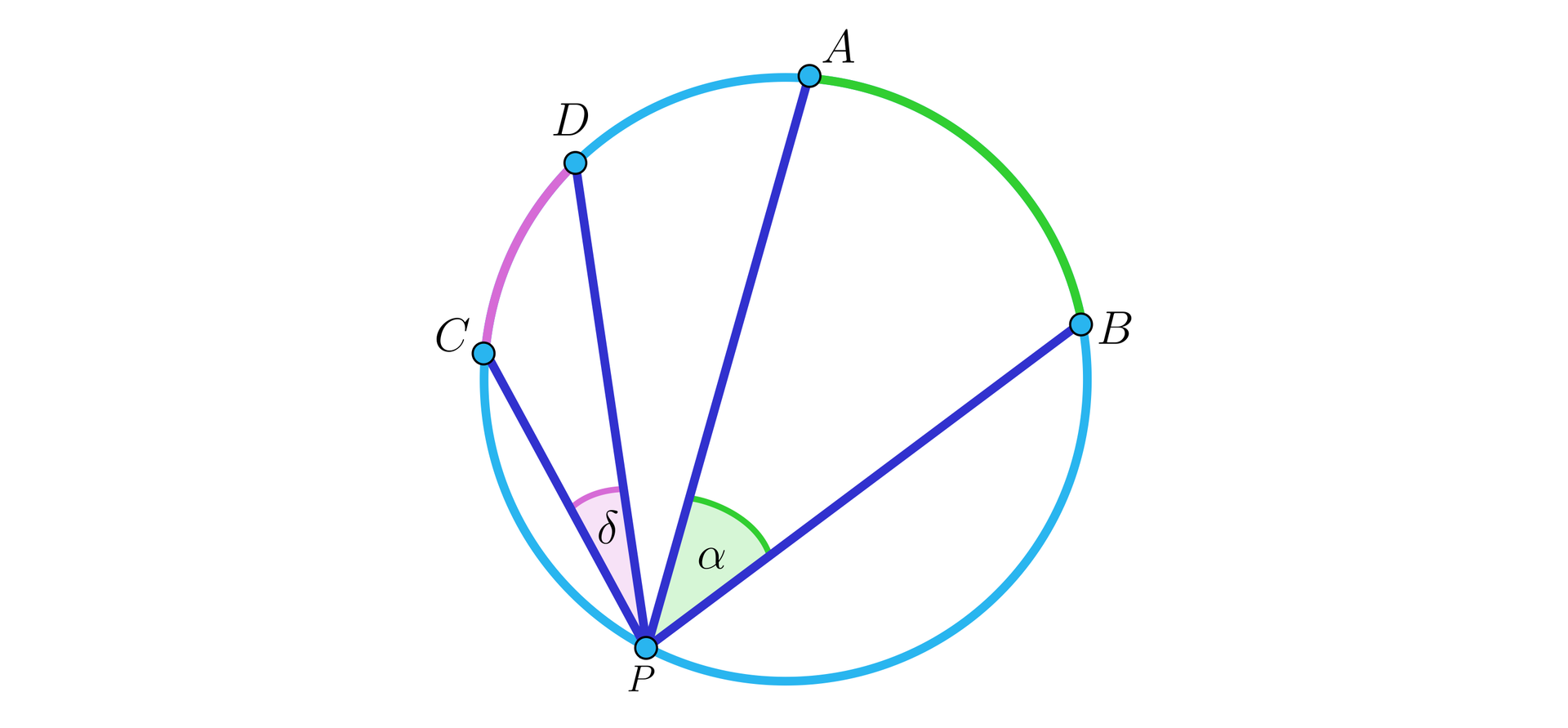
Rysunek przedstawia okrąg, w którym wykreślono cztery cięciwy. Są to kolejno: PC, PD, PA oraz PB. Między cięciwami PC i PD zaznaczono kąt δ oraz zaznaczono łuk między punktami C i D. Między cięciwami PA i PB zaznaczono kąt α oraz zaznaczono łuk między punktami A i B.

Z kolei istnieje nieskończenie wiele kątów wpisanych opartych na danym łuku.

RAC6wKU1j8nqO

Rysunek przedstawia okrąg, w którym wykreślono sześć cięciw opartych na tym samym łuku AB. Cięciwy te to: C3A oraz C3B wyznaczają kąt α3, cięciwy C1A oraz C1B wyznaczają kąt α1, cięciwy C2A oraz C2B wyznaczają kąt α2.

Przykład 1

Dany jest okrąg o środku w punkcie $O$ .

Rozważmy dowolny kąt wpisany oparty na półokręgu $A B$ i poprowadźmy promień $O C$ tego okręgu.

Wówczas trójkąty $A O C$ i $B O C$ są równoramienne.

Oznaczmy: $∢ O A C = α$ oraz $∢ O B C = β$ .

R1TaiEcqhpiNb

Rysunek przedstawia okrąg o środku w punkcie O. Na rysunku zaznaczono dwie cięciwy: CA oraz CB. Pomiędzy punktem A i B zaznaczono średnicę okręgu, a także narysowano promień okręgu: jest to odcinek CO. Na ilustracji oznaczono także kilka kątów. Kąty OAC i kąt ACO są równe α. Kąty OCB i kąt CBO są równe β.

Wtedy: $∢ A O C = 180 ° - 2 α$ oraz $∢ B O C = 180 ° - 2 β$ .

Ale kąty $A O C$ i $B O C$ są kątami przyległymi, zatem $(180 ° - 2 α) + (180 ° - 2 β) = 180 °$ .

Stąd $2 α + 2 β = 180 °$ , czyli $α + β = 90 °$ .

Ale to oznacza, że każdy kąt wpisany w okrągokrągokrąg i oparty na jego średnicy jest kątem prostym, a w konsekwencji, że przeciwprostokątna dowolnego trójkąta prostokątnego jest średnicą okręgu opisanego na tym trójkącie.

Ważne!

Niekiedy zamiast mówić, że kąt jest oparty na łuku, będziemy mówić, że jest na tym łuku rozpięty. W przypadku kąta opartego na półokręgu, często będziemy spotykać się ze stwierdzeniem, że kąt jest rozpięty na średnicy okręgu. Rzadziej pojawia się określenie, że kąt wpisany jest rozpięty na cięciwie, której końcami są końce odpowiedniego łuku okręgułuk okręgułuku okręgu.

Podana w Przykładzie 1 zależność jest szczególnym przypadkiem związku, jaki wiąże kąty wpisane i kąty środkowe oparte na tym samym łuku, co będzie tematem materiału: „Zależność między kątami w kole”.

Rozważmy teraz dowolny okrągokrągokrąg i dwie przecinające się sieczne. Zbadamy związek między tymi siecznymi i utworzonymi przez nie kątami wpisanymi. Rozważmy najpierw przypadek, gdy sieczne przecinają się „wewnątrz” okręgu, tak, jak na poniższym rysunku.

RNb51n0G0MLAb

Rysunek przedstawia okrąg, na którym zaznaczone są następujące punkty kolejno: A, C, N, B, D, M. Na ilustracji zaznaczono trzy cięciwy: CA, CD oraz AB, przy czym cięciwy CD oraz AB przecinają się w punkcie P. Cięciwy te są przedłużone poza okręgiem linią przerywaną. Wewnątrz okręgu oznaczono trzy kąty. Kąt BAC jest oznaczony jako kąt α, kąt ACD jest oznaczony jako kąt β oraz trzecim oznaczonym kątem jest kąt rozwarty APD.

O kącie między siecznymi 1

Twierdzenie: O kącie między siecznymi 1

Kąt $A P D$ , jaki tworzą sieczne, przecinające się w punkcie $P$ , leżącym „wewnątrz” okręgu, jest równy sumie dwóch kątów wpisanych opartych na łukach, z których jeden (łuk $\hat{A M D}$ ) zawarty jest między ramionami kąta, a drugi (łuk $\hat{B N C}$ ) jest zawarty między przedłużeniami ramion tego kąta.

Dowód

Dowód tego twierdzenia jest natychmiastową konsekwencją twierdzenia o kącie zewnętrznym trójkąta.

O kącie między siecznymi 2

Twierdzenie: O kącie między siecznymi 2

Kąt $A P D$ , jaki tworzą sieczne, przecinające się w punkcie $P$ , leżącym na zewnątrz okręgu, jest równy odpowiedniej różnicy dwóch kątów wpisanych opartych na łukach zawartych między ramionami kąta.

Dowód

Popatrzmy na rysunek.

R1KwzDdCL2wjV

Rysunek przedstawia okrąg, na którym zaznaczone są następujące punkty kolejno: A, M, C, D, N, B. Na ilustracji zaznaczono trzy cięciwy: CD, DA oraz AB, przy czym cięciwy CD oraz AB są przedłużone poza okręgiem linią przerywaną tak, że spotykają się w punkcie P leżącym poza okręgiem. Przy punkcie P oznaczono kąt γ pomiędzy przedłużeniem obu cięciw. Wewnątrz okręgu zaznaczono jeszcze dwa inne kąty. Kąt α, czyli kąt CDA oraz kąt β, czyli kąt DAB.

Ponieważ $|∢ A D P| = 180 ° - α$ oraz $γ = 180 ° - β - |∢ A D P|$ , więc $γ = 180 ° - β - (180 ° - α) = α - β$ .

Słownik

okrąg

okręgiem o środku $O$ i promieniu $r$ nazywamy zbiór wszystkich punktów płaszczyzny odległych od punktu $O$ o dany odcinek $r$

koło

kołem o środku $O$ i promieniu $r$ nazywamy zbiór wszystkich punktów płaszczyzny, których odległość od punktu $O$ jest nie większa niż $r$

łuk okręgu

łukiem okręgu nazywamy każdą z dwóch części, na które dzielą okrąg dwa różne punkty leżące na tym okręgu, wraz z tymi punktami

cięciwa okręgu

cięciwą okręgu nazywamy odcinek, którego końce są różnymi punktami leżącymi na tym okręgu

Wprowadzenie

Galeria zdjęć interaktywnych

Słownik