Przeczytaj
Rozważmy dwa okręgi: okrąg o środku w punkcie i promieniu długości oraz okrąg o środku w punkcie i promieniu długości .
Dwa okręgi mające dokładnie jeden punkt wspólny nazywamy stycznymi. Punkt wspólny nazywamy wówczas punktem styczności. Okręgi mogą być styczne zewnętrznie lub styczne wewnętrznie.
Okręgi są styczne zewnętrznie wtedy i tylko wtedy, gdy odległość środków okręgów jest równa sumie długości ich promieni:
Jest to warunek konieczny i wystarczający styczności zewnętrznej dwóch okręgów.

Sprawdzimy, czy okręgi o promieniach , , których odległość między środkami wynosi , są styczne zewnętrznie.
Rozwiązanie
Zauważmy, że zachodzi warunek . Zatem okręgi te są styczne zewnętrznie.
Sprawdzimy, czy okręgi o równaniach i są styczne zewnętrznie.
Rozwiązanie
Okrąg o równaniu ma środek w punkcie i promień długości .
Okrąg o równaniu ma środek w punkcie i promień długości .
Obliczamy odległość środków tych okręgów:
.
Zatem , co oznacza, że okręgi są styczne zewnętrznie.
Dany jest okrąg o równaniu . Wyznaczymy równanie okręgu o środku w punkcie stycznego zewnętrzniestycznego zewnętrznie do okręgu .
Rozwiązanie
Sprowadzamy równanie okręgu do postaci kanonicznej.
Po przekształceniach
otrzymujemy:
.
Stąd: współrzędne środka okręgu : , a jego promień ma długość .
Równanie okręgu o środku w punkcie jest postaci .
Okręgi i są styczne zewnętrznie, więc zachodzi warunek .
Aby obliczyć odległość między środkami okręgów skorzystamy ze wzoru na odległość dwóch punktów: .
Mamy więc:
.
Z warunku wyznaczamy :
, co daje .
Zatem równanie okręgu ma postać: .
Dane są dwa okręgi: o równaniu i o równaniu . Napiszemy równanie okręgu o najmniejszym promieniu, stycznego zewnętrznie do okręgów i .
Rozwiązanie
Środek okręgu stycznego zewnętrznie do okręgów i o najmniejszym promieniu długości jest współliniowy z punktami i , zatem leży na prostej .
Wyznaczymy współrzędne środków okręgów i . W tym celu ich równania zapisujemy w postaci .
:
:
Okrąg ma środek w punkcie i promień długości .
Okrąg ma środek w punkcie i promień długości .
Okrąg ma środek w punkcie i promień długości .
Jeżeli okręgi i są styczne zewnętrznie, to .
Jeżeli okręgi i są styczne zewnętrznie, to .
Przyjmijmy oznaczenia jak na rysunku.
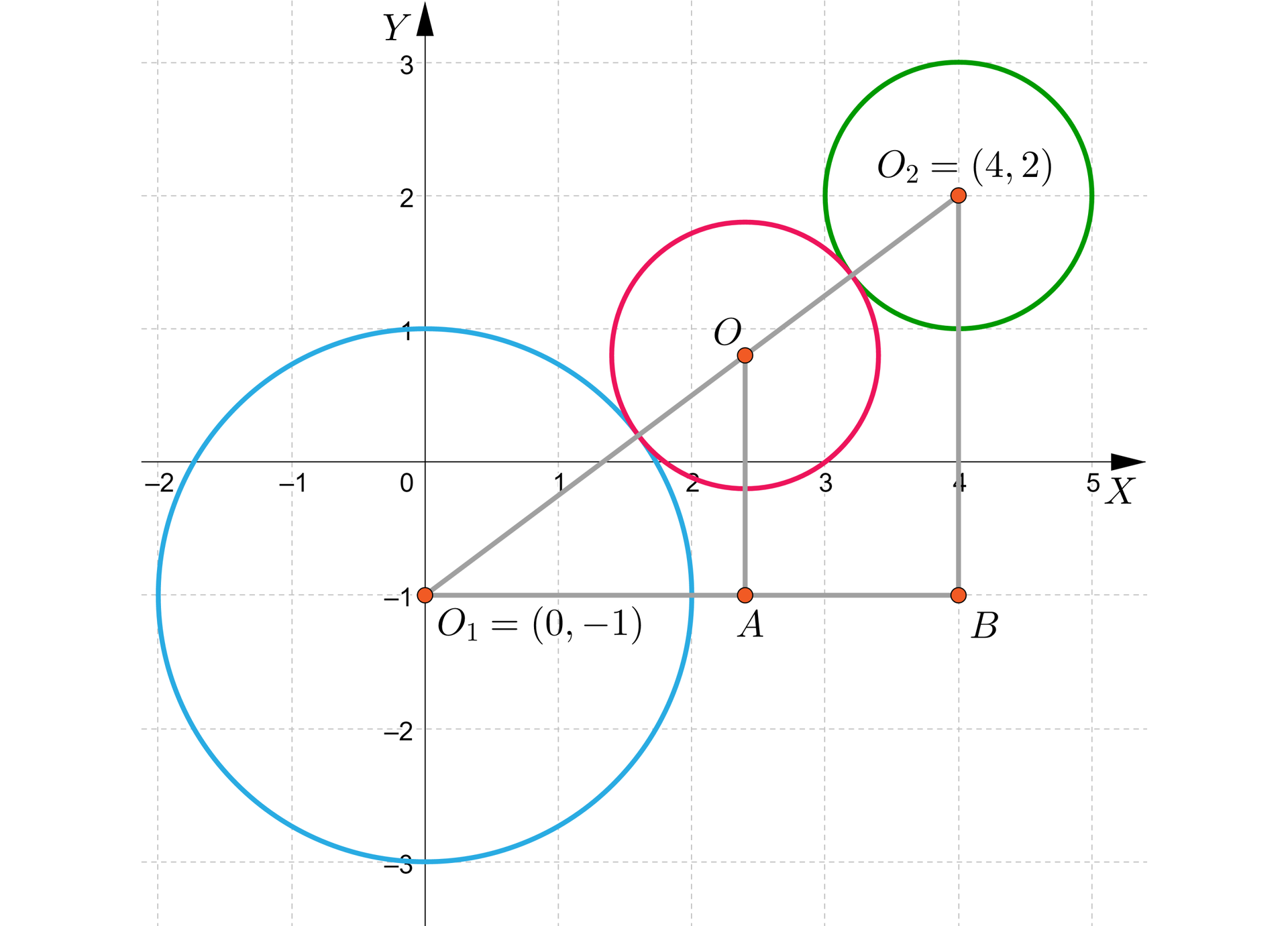
Zauważmy że: , .
Trójkąt jest prostokątny, zatem skorzystamy z twierdzenia Pitagorasa:
.
Ponieważ , i , to
,
stąd , zatem .
Wyznaczamy teraz współrzędne środka okręgu .
Zauważmy, że: , i .
Ponadto, gdy , to , a .
, zatem z twierdzenia Talesa możemy zapisać:
, co daje i stąd ,
, co daje i stąd .
Ponieważ , to .
Równanie szukanego okręgu: .
Dany jest okrąg : i prosta . Wykażemy, że środki okręgów stycznych do danej prostej oraz stycznych zewnętrznie do danego okręgu należą do pewnej paraboli.
Rozwiązanie
Okrąg : ma środek w punkcie oraz promień długości .
Oznaczmy przez okrąg styczny do okręgu i prostej , jego środek przez a długość promienia przez .

Z warunku styczności okręgu do okręgu mamy: , co oznacza, że promień okręgu ma długość .
Długość odcinka wynosi , więc .
Ze styczności okręgu o środku do prostej wynika, że .
Porównując obydwa warunki mamy:
,
stąd .
Zauważmy, że . Wobec tego .
Podnosząc obie strony równości do kwadratu otrzymujemy:
,
czyli .
Obrazem geometrycznym szukanego zbioru jest parabola określona wzorem .
Dany jest okrągokrąg o środku w punkcie i promieniu długości oraz dwa okręgi położone tak, jak na rysunku.

Obliczymy obwód trójkąta, którego wierzchołkami są środki tych okręgów.
Rozwiązanie
Okrąg ma środek w punkcie i promień długości .
Okrąg ma środek w punkcie i promień długości .
Okrąg ma środek w punkcie i promień długości .
Obwód trójkąta jest sumą długości jego boków: .
Okręgi i są styczne wewnętrznie, więc .
Okręgi i są styczne wewnętrznie, więc .
Okręgi i są styczne zewnętrznie, więc .
Zatem .
Obwód trójkąta przedstawionego na rysunku wynosi .
Słownik
zbiór wszystkich punktów płaszczyzny, których odległość od punktu jest równa
dwa okręgi są styczne zewnętrznie, gdy odległość środków tych okręgów jest równa sumie długości ich promieni