Przeczytaj
W różny sposób definiujemy skończone i nieskończone granice funkcji w nieskończoności. Przypomnijmy na początek dwie równoważne definicje skończonych granic funkcji w nieskończoności: według Heinego i Cauchy’ego.
Mówimy, że funkcja ma w granicę skończoną równą , gdy dla dowolnego ciągu argumentów dążących do , wartości funkcji dążą do .
Mówimy, że funkcja ma w granicę skończoną równą , gdy dla dowolnie małej dodatniej liczby istnieje taka liczba dodatnia , że dla wszystkich argumentów większych od wartości funkcji są pomiędzy i .
Symbolicznie zapisujemy to jako
Podobnie definiujemy granicę skończoną w .
Sprawdzimy, używając definicji Heinego, czy funkcja , , ma w granicę skończonągranicę skończoną równą .
Rozwiązanie
Weźmy dowolny ciąg argumentów dążący .
Wówczas wiemy, że ciąg kwadratów tych argumentów, , również dąży do . Zatem ciąg odwrotności kwadratów, , dąży do , czyli granicą funkcji w jest ,
.
Sprawdzimy, używając definicji Cauchy’ego, czy funkcja , , ma w granicę skończonągranicę skończoną równą .
Rozwiązanie
Weźmy dowolnie małą liczbę dodatnią . Jeżeli zdefiniujemy liczbę dodatnią jako odwrotność pierwiastka z , czyli , to wówczas dla wszystkich argumentów większych od wartości funkcji są nie mniejsze od i nie większe od , i tym samym granicą funkcji w jest .
Możemy sprawdzić empirycznie, jak wygląda znajdowanie wartości w zależności od wartości na przykładzie funkcji , .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DrhcVbhWs
Jak widać, im mniejsza wartość , tym większa jest wartość – w dalszym miejscu leżą argumenty, dla których wartości funkcji są pomiędzy zadanymi liniami – ale za każdym razem można taką wartość znaleźć.
Przypomnijmy teraz dwie równoważne definicje nieskończonych granic funkcji w nieskończoności: według Heinego i Cauchy’ego.
Mówimy, że funkcja ma w granicę nieskończoną równą , gdy dla dowolnego ciągu argumentów , dążących do , wartości dążą do .
Mówimy, że funkcja ma w granicę nieskończoną równą , gdy dla dowolnie dużej dodatniej liczby istnieje taka liczba dodatnia , że dla wszystkich argumentów większych od wartości funkcji są większe od .
Symbolicznie zapisujemy to jako
Podobnie definiujemy granicę nieskończoną równą , oraz obie granice nieskończone w .
Sprawdzimy, używając definicji Heinego, czy funkcja ma w granicę nieskończonągranicę nieskończoną równą .
Rozwiązanie
Weźmy dowolny ciąg argumentów dążący do . Wówczas wiemy, że ciąg kwadratów tych argumentów, , również dąży do . Zatem ciąg kwadratów pomniejszonych o jeden, , również dąży do , czyli granicą funkcji w jest ,
.
Sprawdzimy, używając definicji Cauchy’ego, czy funkcja ma w granicę nieskończonągranicę nieskończoną równą .
Rozwiązanie
Weźmy dowolnie dużą liczbę dodatnią . Jeżeli zdefiniujemy liczbę dodatnią jako pierwiastek z liczby powiększonej o jeden, czyli , to wówczas dla wszystkich argumentów większych od wartości funkcji są nie mniejsze od , i tym samym granicą funkcji w jest .
Nie zawsze funkcja musi mieć granicę w nieskończoności, przykładami mogą być podstawowe funkcje trygonometryczne.
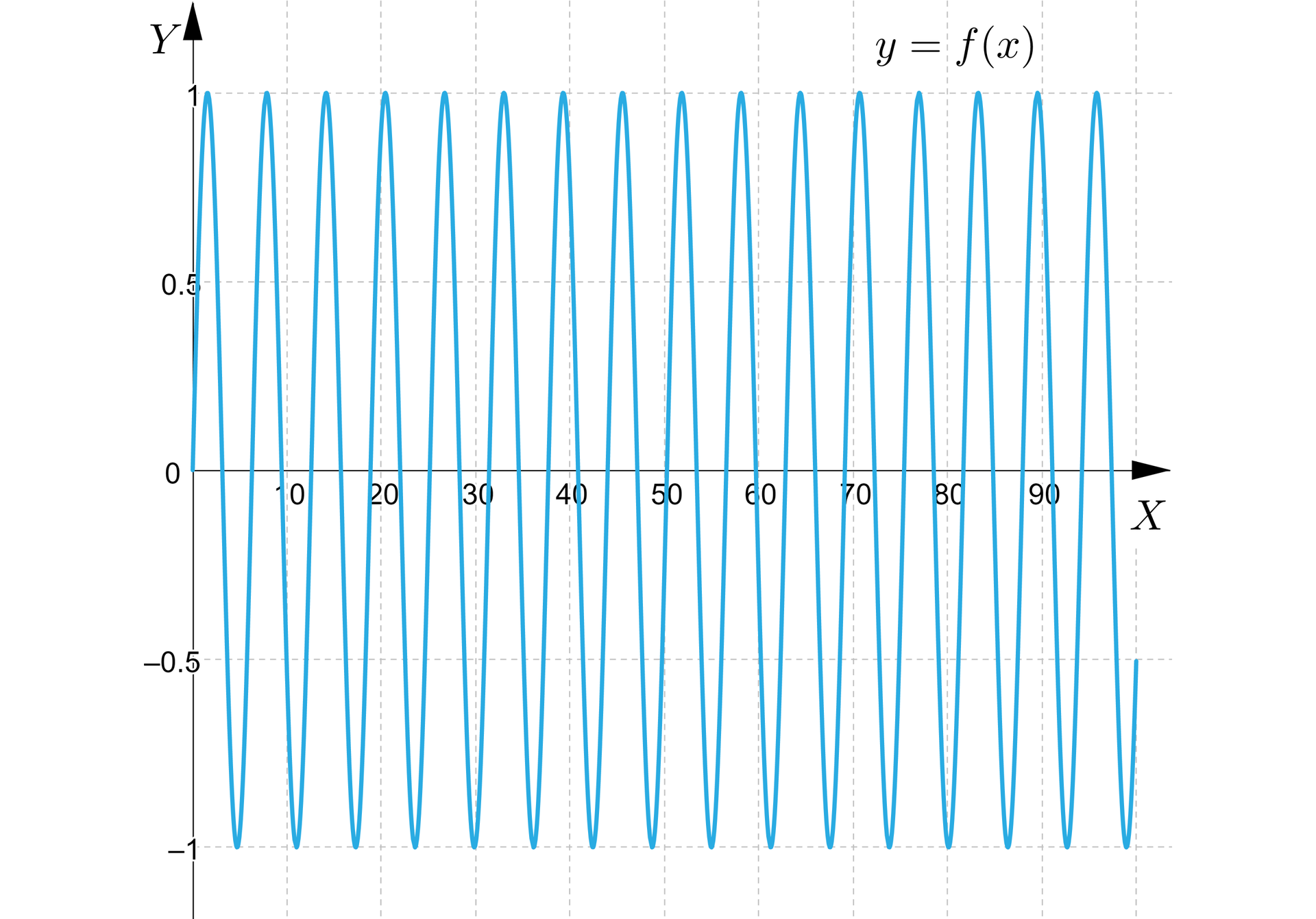
Funkcja sinus nie ma granicy w nieskończoności. Rozważmy dwa dowolne ciągi argumentów dążące do :
Zauważmy, że dla dążącego do ciąg dąży do , zaś ciąg dąży do .
To wystarczy, żeby udowodnić, że nie istnieje.
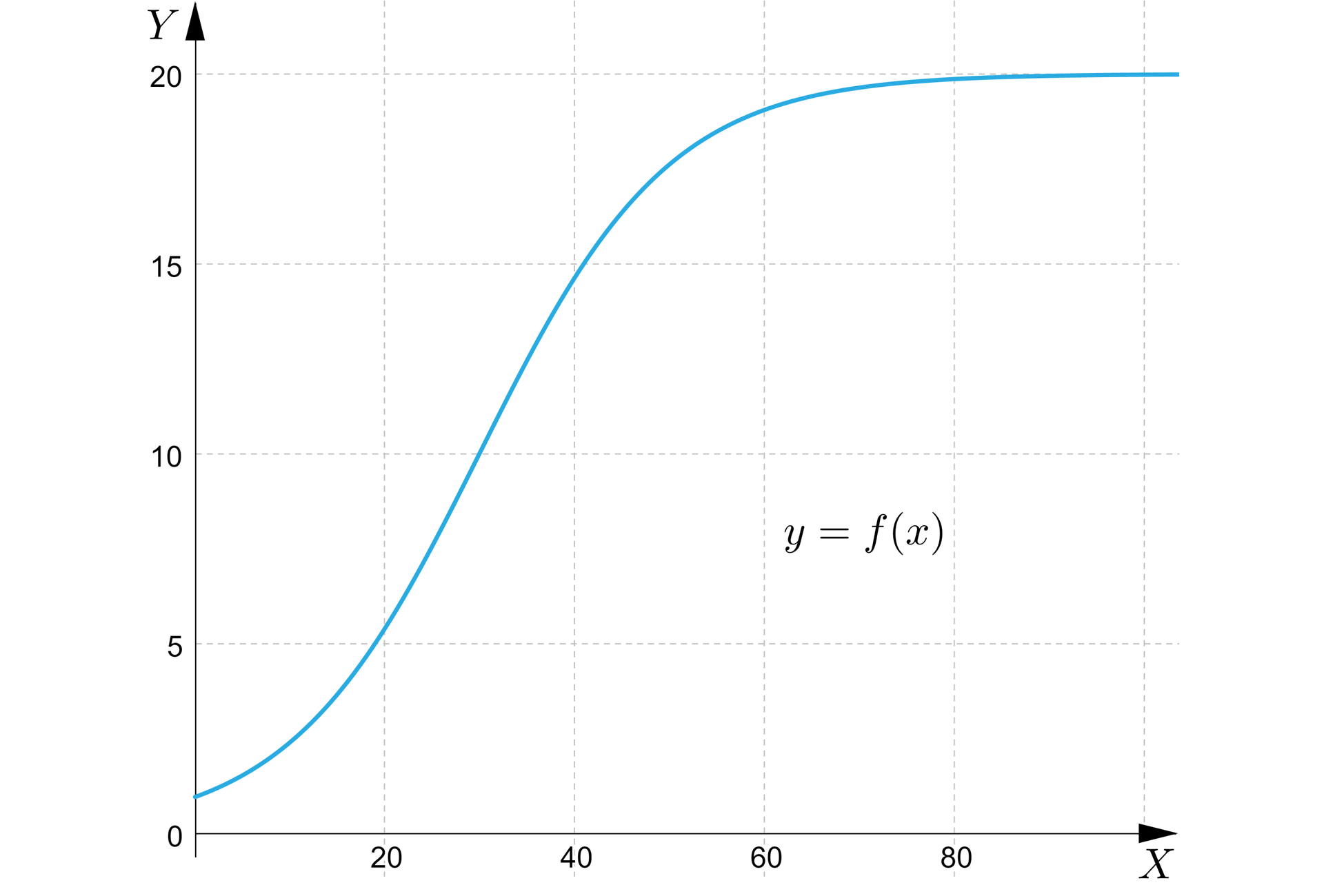
Wyjaśnienie paradoksu wzrostu
Jak pamiętamy, T. Malthus próbował szacować wzrost populacji ludzi na świecie i otrzymany wynik wydawał się rosnąć w sposób niekontrolowany. Prawdopodobnie w czasach Malthusa nie zdawano sobie sprawy, że funkcja może być jednocześnie rosnąca i ograniczona z góry (przyjąć ten fakt pomogły nam dopiero rozważania dotyczące granic funkcji, które prowadzili niezależnie Augustin Cauchy i Heindrich Heine). Formułując rozważania dotyczące nieskończoności, błędem jest oglądanie tylko najbliższego otoczenia aktualnego momentu czasu na wykresie, gdyż przy względnie małych wartościach argumentów wartości funkcji wydawały się rosnąć nieograniczenie. Dopiero wyznaczenie granicy w nieskończoności pokazało nam długoterminowe zachowanie wartości naszej funkcji.
Słownik
granica funkcji w nieskończoności ( lub ), która jest liczbą rzeczywistą
granica funkcji w nieskończoności ( lub ), która jest nieskończona ( lub )