Wykresem równania pierwszego stopnia z dwiema niewiadomymi $x$ i $y$

gdzie $a, b, c\in \mathrm{ℝ}$ i $a^2+b^2\ne 0$.

nazywamy zbiór wszystkich punktów, których współrzędne $\left(x,y\right)$ spełniają to równanie.

Zapiszmy symbolicznie podane zależności.

• Suma dwóch liczb $x$ i $y$ jest większa od $4$.
  $x+y>4$

• Różnica podwojonej liczby $x$ oraz trzykrotności liczby $y$ jest nie mniejsza od liczby $x$.
  $2x-3y\ge x$

• Suma $95\%$ liczby $x$ oraz $45\%$ liczby $y$ jest nie większa od różnicy liczb $x$ i $y$.
  $0,95x+0,45y\le x-y$

• Różnica liczb $x$ oraz $y$ jest mniejsza od połowy sumy tych liczb.
  $x-y<\frac{1}{2}·\left(x+y\right)$.

Nierównością pierwszego stopnia z dwiema niewiadomymi nazywamy każdą nierówność, którą możemy przedstawić w postaci:

gdzie $a, b, c\in \mathrm{ℝ}$ i $a^2+b^2\ne 0$ ($a$ i $b$ nie mogą być jednocześnie zerami).

Sprawdzimy, współrzędne których punktów $A=\left(1,1\right)$, $B=\left(3,4\right)$, $C=\left(-2,0\right)$ oraz $D=\left(\mathrm{2,}0\right)$ spełniają nierówność

$2x-y>x-1$.

Po lewej stronie nierówności znajduje się wyrażenie $2x-y$, po prawej $x-1$.

Sprawdzimy, czy po podstawieniu współrzędnych punktów odpowiednio $A$, $B$, $C$ oraz $D$ otrzymamy nierówności prawdziwe.

• $A=\left(1, 1\right)$
  $L=2x-y=2-1=1$
  $P=x-1=1-1=0$
  Nierówność $L>P$ jest prawdziwa, więc współrzedne punktu $A$ spełniają nierówność.  
  $2x-y>x-1$.

• $B=\left(3, 4\right)$
  $L=2x-y=6-4=2$
  $P=x-1=3-1=2$
  Nierówność $L>P$ nie jest prawdziwa, więc współrzedne punktu $B$ nie spełniają nierówności 
  $2x-y>x-1$.

• $C=\left(-2, 0\right)$
  $L=2x-y=-4-0=-4$
  $P=x-1=-2-1=-3$
  Nierówność $L>P$ nie jest prawdziwa, więc współrzedne punktu $C$ nie spełniają nierówności
  $2x-y>x-1$.

• $D=\left(\mathrm{2,} 0\right)$
  $L=2x-y=4-0=4$
  $P=x-1=2-1=1$
  Nierówność $L>P$ jest prawdziwa, więc współrzedne punktu $D$ spełniają nierówność 
  $2x-y>x-1$.

W prostokątnym układzie współrzędnych zaznaczmy wszystkie zbiory punktów, których współrzędne spełniają podane niżej nierówności.

• $x+y\ge 2$:

Przekształcamy nierówność równoważnie do postaci $y\ge -x+2$.

Nierówność $y\ge -x+2$ jest równoważna alternatywie warunków:

$y>-x+2$ lub $y=-x+2$

Narysujmy najpierw wykres równania $y=-x+2$.

RwhMGmdqtu7lg

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie narysowano ukośną prostą opisaną wzorem $y=-x+2$, która przechodzi przez dwa charakterystyczne punkty: $\left(2;0\right)$ oraz $\left(0;2\right)$.

Prosta o równaniu $y=-x+2$ podzieliła płaszczyznę na dwie półpłaszczyzny.

Na płaszczyźnie ponad prostą znajdują się wszystkie punkty, których współrzędne spełnią warunek $y>-x+2$, a na drugiej – poniżej prostej – punkty, których współrzędne spełnią warunek $y<-x+2$.

Aby upewnić się, czy wybieramy dobrą półpłaszczyznę, możemy wybrać dowolny punkt do niej należący i sprawdzić, czy jego współrzędne spełnią odpowiednią nierówność.

Wybieramy np. punkt $A=\left(0, 3\right)$ i sprawdzamy:

$L=y=3$

$P=-x+2=0+2=2$

Otrzymaliśmy zdanie prawdziwe $L>P$, a zatem wybrany przez nas punkt należy do właściwej półpłaszczyzny.

R1NydfcZS4h2d

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie narysowano ukośną prostą opisaną wzorem $y=-x+2$, która przechodzi przez dwa charakterystyczne punkty: $\left(2;0\right)$ oraz $\left(0;2\right)$. Dodatkowo zaznaczono na płaszczyźnie punkt $A$ o współrzędnych $\left(0;3\right)$ leżący nad prostą.

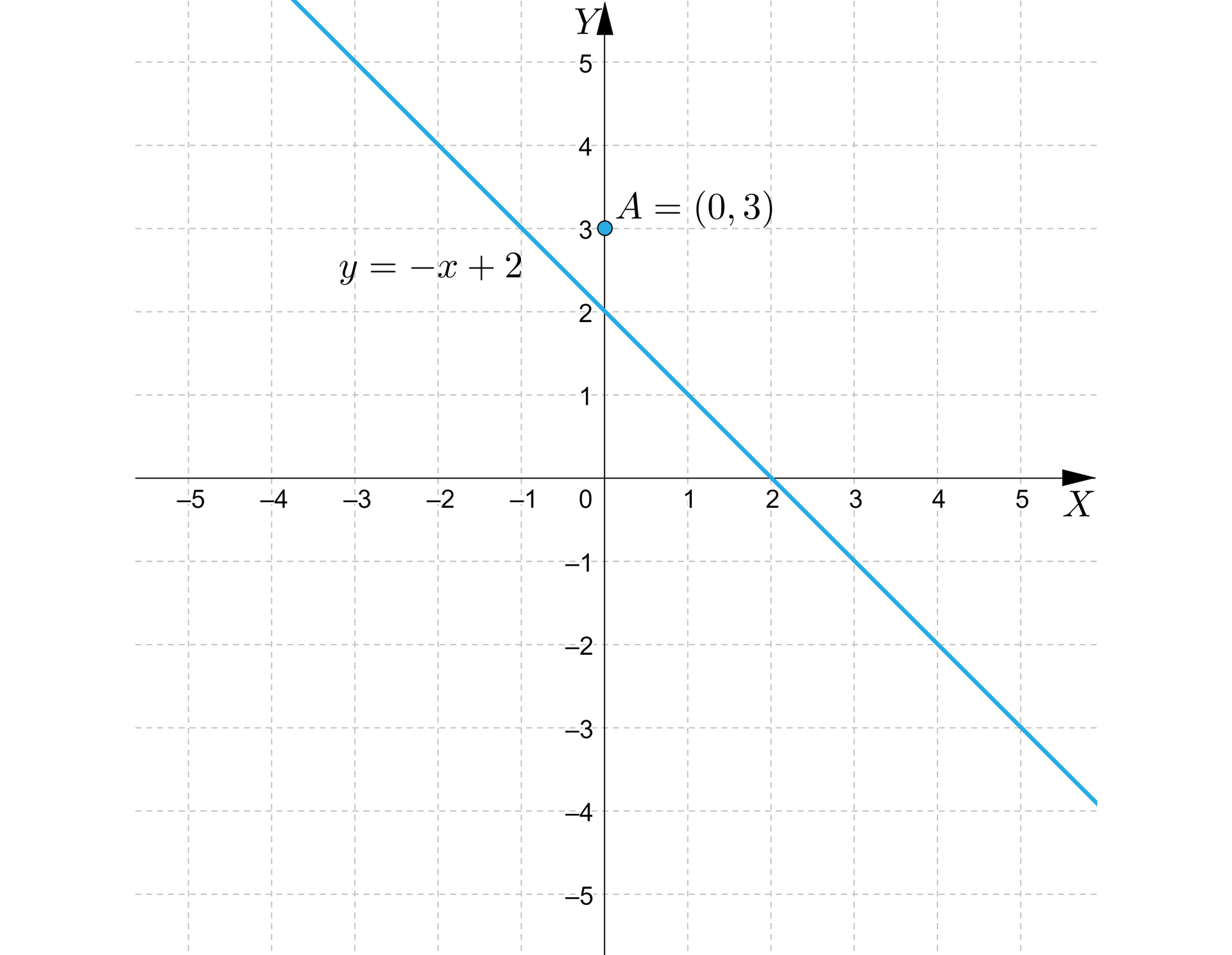
Zaznaczamy zatem półpłaszczyznę, do której należy punkt $A$ oraz prostą, oznaczoną linią ciągłą. Zaznaczony obszar jest zbiorem wszystkich punktów, których współrzędne spełniają nierówność   $y\ge -x+2$.

R1HS8IrndYBI7

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie narysowano ukośną prostą opisaną wzorem $y=-x+2$, która przechodzi przez dwa charakterystyczne punkty: $\left(2;0\right)$ oraz $\left(0;2\right)$. Dodatkowo zaznaczono na płaczyźnie punkt $A$ o współrzędnych $\left(0;3\right)$. Nad prostą, czyli w kierunku rosnących arumentów oraz wartości, zamalowano płaszczyznę. Jest zbiór opisany nierównością $y\ge -x+2$.

• $-2x+y\le -4$:

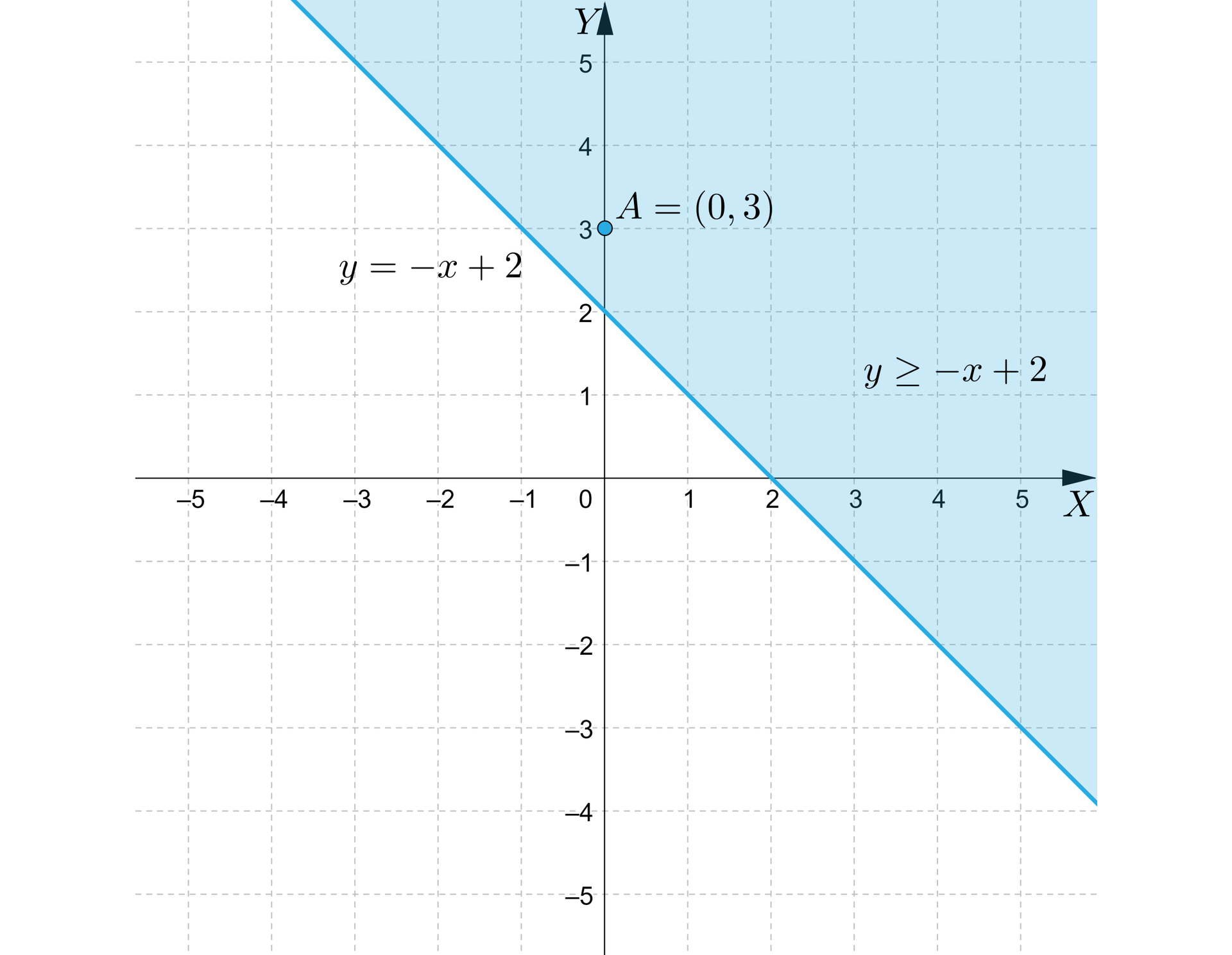
Przekształcamy nierówność równoważnie do postaci $y\le 2x-4$.

Nierówność $y\le 2x-4$ jest równoważna alternatywie warunków:

$y<2x-4$ lub $y=2x-4$

Narysujmy najpierw wykres równania $y=2x-4$.

Aby wybrać właściwą półpłaszczyznę, wybieramy dowolny punkt leżący poza prostą i sprawdzamy, czy jego współrzędne spełnią odpowiednią nierówność.

Wybieramy np. punkt $A=\left(2, -2\right)$ i sprawdzamy:

$L=y=-2$

$P=2x-4=4-4=0$

Otrzymaliśmy zdanie prawdziwe $L<P$, a zatem wybrany przez nas punkt należy do półpłaszczyzny zawierającej punkty spełniające nierówność.

R1DBvHsugcYWq

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie narysowano ukośną prostą opisaną wzorem $y=2x-4$, która przechodzi przez dwa charakterystyczne punkty: $\left(2;0\right)$ oraz $\left(0;-4\right)$. Dodatkowo zaznaczono na płaczyźnie punkt $A$ o współrzędnych $\left(2;-2\right)$ leżący pod prostą.Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie narysowano ukośną prostą opisaną wzorem $y=2x-4$, która przechodzi przez dwa charakterystyczne punkty: $\left(2;0\right)$ oraz $\left(0;-4\right)$. Dodatkowo zaznaczono na płaszczyźnie punkt $A$ o współrzędnych $\left(2;-2\right)$ leżący pod prostą. Część płaszcyzny znajdującą się pod prostą wraz z prostą zamalowano. Jest to zbiór, który opisuje nierówność $y\le 2x-4$.

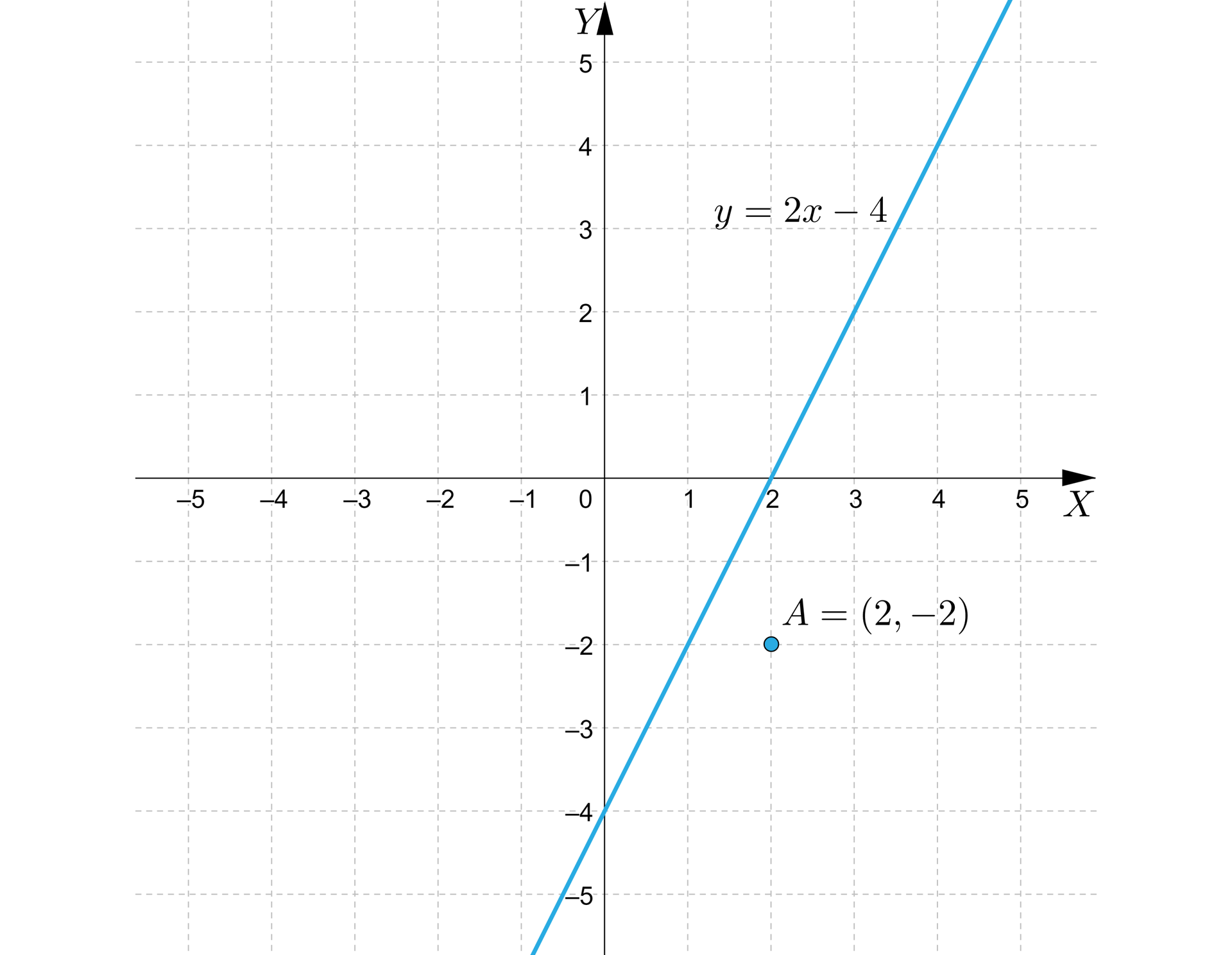
Zaznaczamy zatem półpłaszczyznę, do której należy punkt $A$ oraz oznaczamy linią ciągłą prostą. Zaznaczony obszar jest zbiorem wszystkich punktów, których współrzędne spełniają nierówność   $-2x+y\le -4$.

R1Sx1zb3tChwe

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie narysowano ukośną prostą opisaną wzorem $y=2x-4$, która przechodzi przez dwa charakterystyczne punkty: $\left(2;0\right)$ oraz $\left(0;-4\right)$. Dodatkowo zaznaczono na płaczyźnie punkt $A$ o współrzędnych $\left(2;-2\right)$ leżący pod prostą. Część płaszcyzny znajdującą się pod prostą wraz z prostą zamalowano. Jest to zbiór, który opisuje nierówność $y\le 2x-4$.

• $3x-2·\left(y+x\right)>4-3y$:

Przekształcamy nierówność równoważnie.

$3x-2y-2x>4-3y$

$-2y+3y>-x+4$

$y>-x+4$

Narysujmy najpierw wykres równania $y=-x+4$.

W tym przypadku punkty leżące na prostej nie należą do wykresu nierówności, ponieważ jest to nierówność ostra.

Aby wybrać właściwą półpłaszczyznę, wybieramy dowolny punkt leżący poza prostą i sprawdzamy, czy jego współrzędne spełnią odpowiednią nierówność.

Wybieramy np. punkt $A=\left(1, 5\right)$ i sprawdzamy:

$L=y=5$

$P=-x+4=-1+4=3$

Otrzymaliśmy zdanie prawdziwe $L>P$, a zatem wybrany przez nas punkt należy do właściwej półpłaszczyzny.

Ru02LFeEkPoYs

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie narysowano ukośną prostą opisaną wzorem $y=-x+4$, która przechodzi przez dwa charakterystyczne punkty: $\left(4;0\right)$ oraz $\left(0;4\right)$. Dodatkowo zaznaczono na płaszczyźnie punkt $A$ o współrzędnych $\left(1;5\right)$ leżący nad prostą.

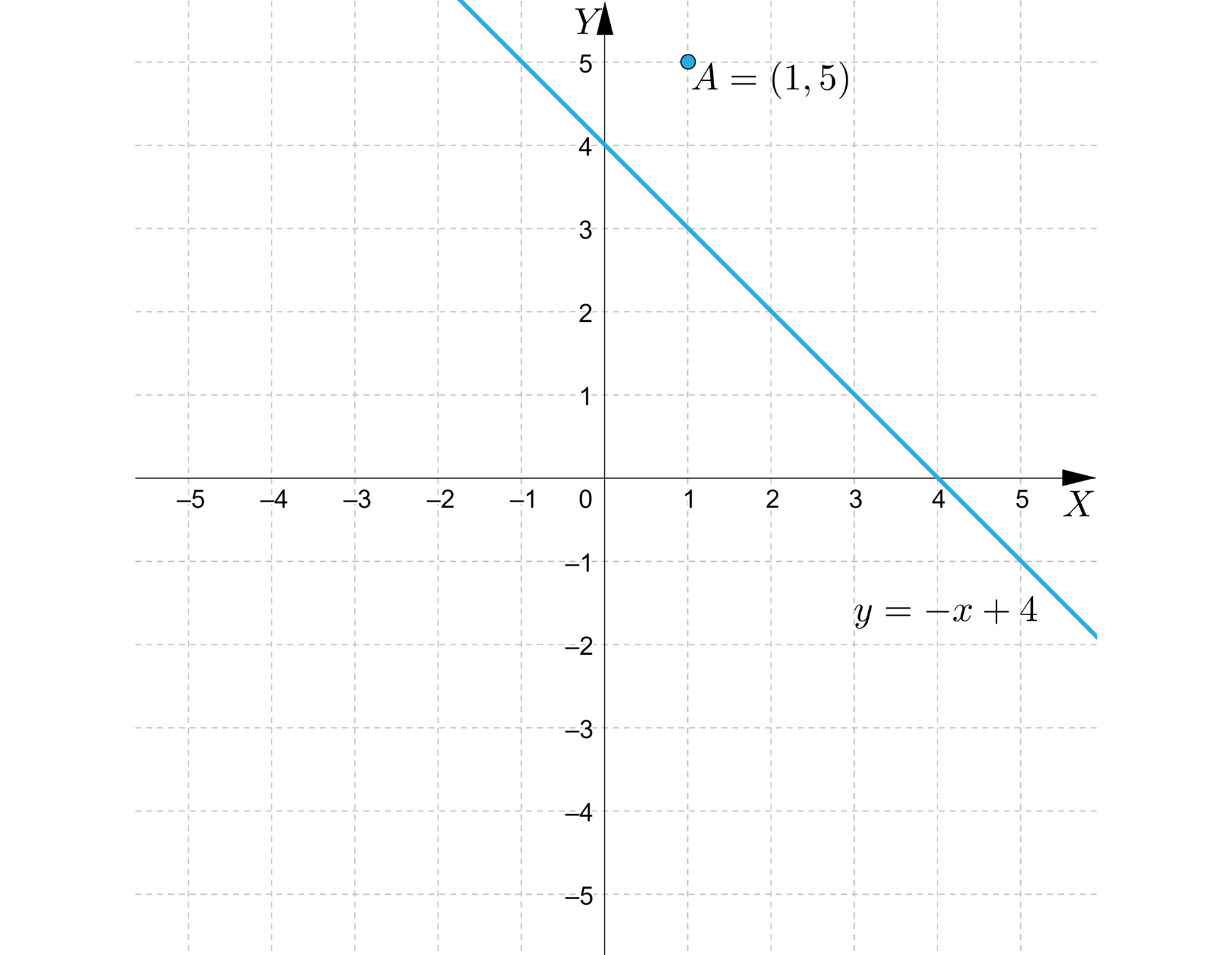
Zaznaczamy zatem półpłaszczyznę, do której należy punkt $A$ oraz prostą oznaczoną linią przerywaną. Zaznaczony obszar jest zbiorem wszystkich punktów, których współrzędne spełniają nierówność   $3x-2·\left(y+x\right)>4-3y$.

RnGDpuwKRtVlU

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie linią przerywaną narysowano ukośną prostą opisaną wzorem $y=-x+4$, która przechodzi przez dwa charakterystyczne punkty: $\left(4;0\right)$ oraz $\left(0;4\right)$. Dodatkowo zaznaczono na płaszczyźnie punkt $A$ o współrzędnych $\left(1;5\right)$ leżący nad prostą. Na płaszczyźnie zamalowano obszar znajdujący się nad prostą. Jako, że prosta narysowana jest linią przerywaną, to umownie nie należy do tego obszaru. Obaszr opisuje nierówność $y>-x+4$.

• $3y<6x-3$:

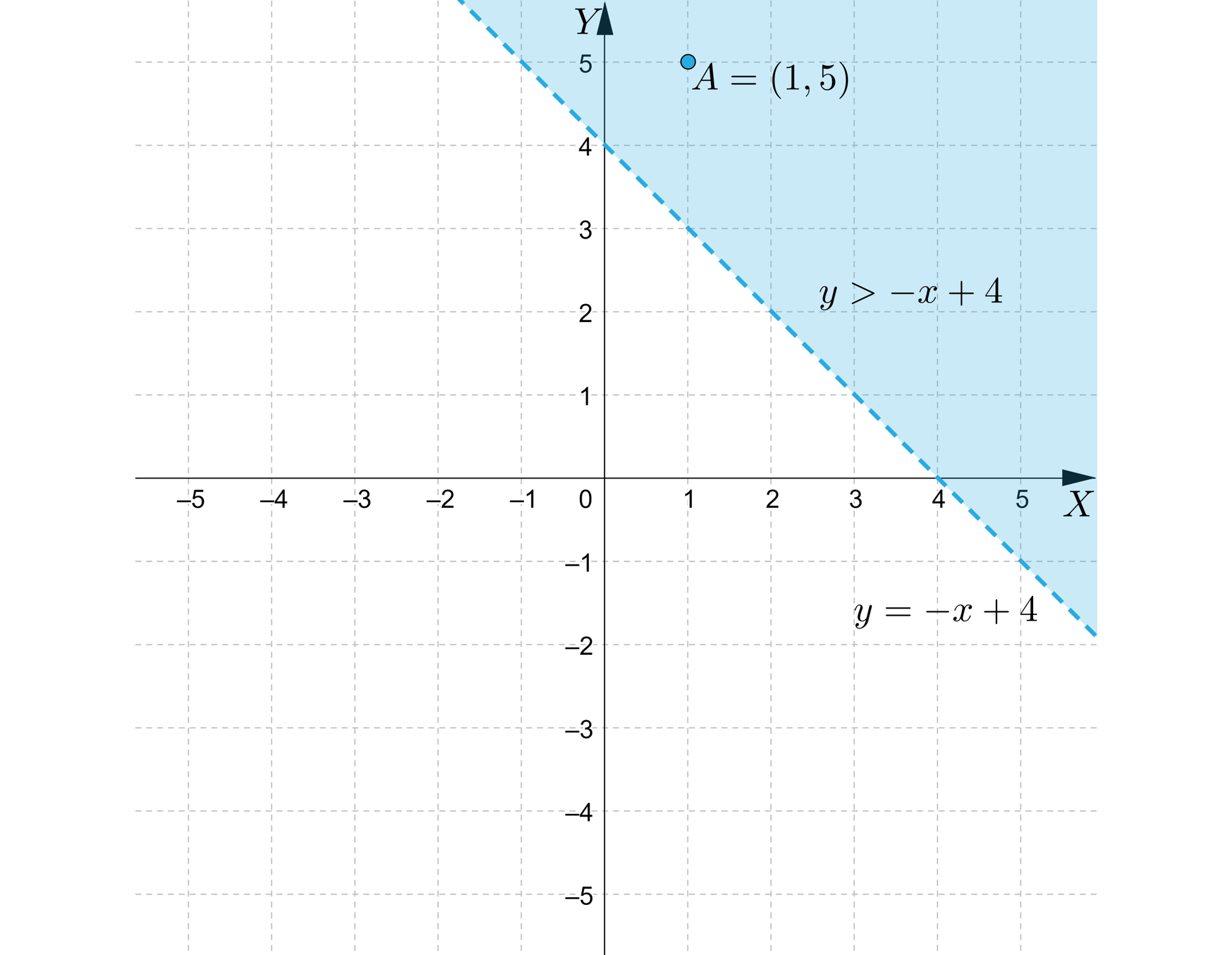
Przekształcamy nierówność równoważnie.

$3y<6x-3|:3$

$y<2x-1$

Narysujmy najpierw wykres równania $y=2x-1$.

Aby wybrać właściwą półpłaszczyznę, wybieramy dowolny punkt leżący poza prostą i sprawdzamy, czy jego współrzędne spełnią odpowiednią nierówność.

Wybieramy np. punkt $A=\left(0, 2\right)$ i sprawdzamy:

$L=y=2$

$P=2x-1=0-1=-1$

Nierówność $2<-1$ jest fałszywa, a zatem wybrany przez nas punkt nie należy do właściwej półpłaszczyzny.

RBNu9xk2n0q2f

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie narysowano ukośną prostą opisaną wzorem $y=2x-1$, która przechodzi przez dwa charakterystyczne punkty: $\left(\frac{1}{2};0\right)$ oraz $\left(0;-1\right)$. Dodatkowo zaznaczono na płaszczyźnie punkt $A$ o współrzędnych $\left(0;2\right)$ leżący nad prostą.

Musimy więc zaznaczyć tę półpłaszczyznę, do której nie należy punkt $A$.

Ponieważ nierówność jest ostra, więc krawędź półpłaszczyzny oznaczymy linią przerywaną.

R17mTOOqt6iIe

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie linią przerywaną narysowano ukośną prostą opisaną wzorem $y=2x-1$, która przechodzi przez dwa charakterystyczne punkty: $\left(\frac{1}{2};0\right)$ oraz $\left(0;-1\right)$. Dodatkowo zaznaczono na płaszczyźnie punkt $A$ o współrzędnych $\left(0;2\right)$ leżący nad prostą. Część płaszczyzny pod prostą zamalowano. Jako, że prosta narysowana jest linią przerywaną, to nie należy do zamalowanego obszaru. Zamalowana część płaszczyzny jest zbiorem opisanym nierównością $y<2x-1$.

Zaznaczony obszar jest zbiorem wszystkich punktów, których współrzędne spełniają nierówność   $3y<6x-3$.

W prostokątnym układzie współrzędnych zaznaczmy zbiór wszystkich punktów, których współrzędne spełniają podane niżej nierówności.

• $x+2>0$

Przekształcamy nierówność równoważnie do postaci $x>-2$.

Szkicujemy prostą o równaniu $x=-2$ linią przerywaną.

Rozwiązaniem nierówności są punkty $\left(x, y\right)$, których współrzędne spełniają warunki:

$x>-2$ i $y\in \mathrm{ℝ}$

A więc np. punkt $A=\left(\mathrm{0,} 0\right)$ należy do zbioru rozwiązań tej nierówności. Zaznaczamy półpłaszczyznę, do której należy punkt $A$.

R1bZHwwgWlEno

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus pięciu do pięciu. Na płaszczyźnie linią przerywaną narysowano pionową prostą opisaną wzorem $x=-2$, która przechodzi przez charakterystyczny punkt o współrzędnych $\left(-2;0\right)$. Dodatkowo zaznaczono na płaszczyźnie punkt $A$ o współrzędnych $\left(0;0\right)$ leżący na prawo od prostej. Część płaszczyzny na prawo od prostej zamalowano. Jako, że prosta narysowana jest linią przerywaną, to nie należy do zamalowanego obszaru. Zamalowana część płaszczyzny jest zbiorem opisanym nierównością $x>-2$.

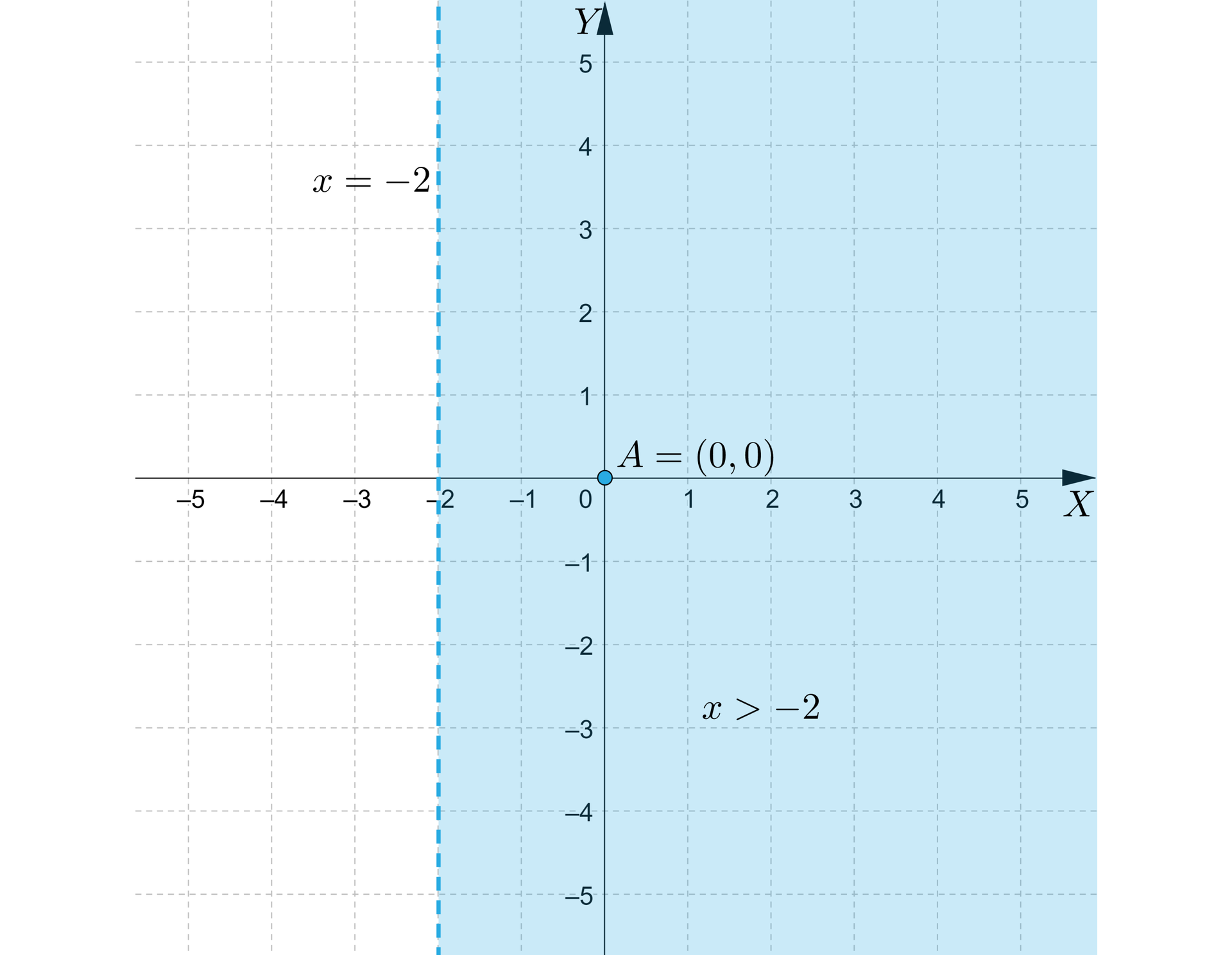
Zaznaczony obszar jest interpretacją geometryczną nierówności $x+2>0$.

• $y-4\le 2$

Przekształcamy nierówność równoważnie do postaci $y\le 6$.

Szkicujemy prostą o równaniu $y=6$ linią ciągłą.

Rozwiązaniem nierówności są punkty $\left(x, y\right)$, których współrzędne spełniają warunki:

$x\in \mathrm{ℝ}$ i $y\le 6$.

A więc np. punkt $A=\left(\mathrm{0,} 0\right)$ należy do zbioru rozwiązań tej nierówności. Zaznaczamy półpłaszczyznę, do której należy punkt $A$.

R4lCTZ3SfMiXu

Ilustracja przedstawia wykres z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus dwóch do ośmiu. Na płaszczyźnie narysowano poziomą prostą opisaną wzorem $y=6$, która przechodzi przez charakterystyczny punkt o współrzędnych $\left(0;6\right)$. Dodatkowo zaznaczono na płaszczyźnie punkt $A$ o współrzędnych $\left(0;0\right)$ leżący poniżej prostej. Część płaszczyzny poniżej prostej zamalowano. Jako, że prosta narysowana jest linią ciągłą, to należy do zamalowanego obszaru. Zamalowana część płaszczyzny jest zbiorem opisanym nierównością $y\le 6$.

Zaznaczony obszar jest interpretcją geometryczną  nierówności $y-4\le 2$.

Uogólnijmy teraz pojęcie ilustracji geometrycznej nierówności pierwszego stopnia z dwiema niewiadomymi.

Rozpatrzmy prostą l będącą wykresem równania $ax+by=c$, gdzie $a\ne 0$ i $b\ne 0$.

Prosta ta dzieli płaszczyznę na dwie półpłaszczyzny.

Obierzmy punkty $P=\left(x_P, y_P\right)$, $R=\left(x_R, y_R\right)$ oraz $S=\left(x_S, y_S\right)$, tak aby odcięte tych punktów były sobie równe oraz aby punkt $P$ leżał na prostej $l$, punkt $R$ nad prostą, a punkt $S$ poniżej prostej $l$.

RuazdVMBJSYmH

Ilustracja przedstawia wykres z poziomą osią $X$ oraz z pionową osią $Y$ bez podziałki. Na płaszczyźnie narysowano dwie proste. Ukośna narysowana jest linią ciągłą i opisuje ją wzór $l: ax+by=c$. Prosta $l$ przechodzi przez pierwszą, drugą i trzecią ćwiartkę układu. Druga, pionowa prosta, narysowana jest linią przerywaną i jest prostą pomocniczą poprowadzoną przez trzy zaznaczone na płaszczyźnie punkty. Prosta ta przechodzi przez pierwszą i czwartą ćwiartkę układu. Punkty zaznaczone na płaszczyźnie, które znajdują się pionowej prostej pomocniczej znajdują się w pierwszej ćwiartce i są to kolejno od góry: $R=\left(x_R;y_R\right), P=\left(x_P;y_P\right), S=\left(x_S;y_S\right)$, przy czym punkt $P$ należy również do prostej $l$.

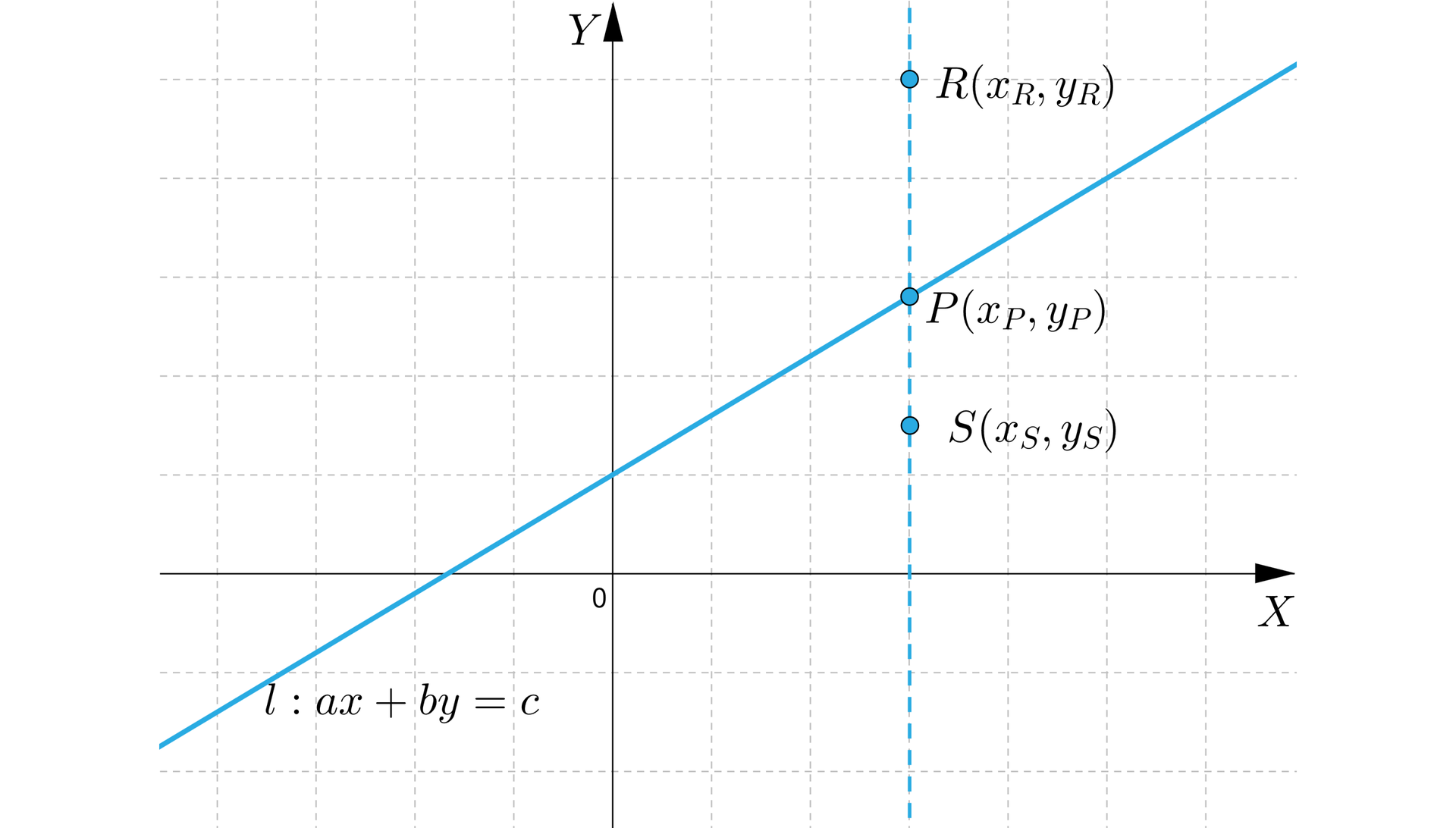
Przyjmijmy, że

$x_P=x_R=x_S=x$.

Zauważmy, że:

$y_R>y_P$
i
$a{x}_P+b{y}_P=c$
$y_P=-\frac{a}{b}{x}_P+\frac{c}{b}=-\frac{a}{b}x+\frac{c}{b}$

Więc:

$y_R>-\frac{a}{b}x+\frac{c}{b}=\frac{-a}{b}{x}_R+\frac{c}{b}|\cdot b$

I stąd

$a{x}_R+b{y}_R>c$

Analogicznie:

$y_S<y_P$
i
$a{x}_P+b{y}_P=c$
$y_P=-\frac{a}{b}{x}_P+\frac{c}{b}=-\frac{a}{b}x+\frac{c}{b}$

Więc

$y_S<-\frac{a}{b}x+\frac{c}{b}=\frac{-a}{b}{x}_S+\frac{c}{b}|\cdot b$

I stąd

$a{x}_S+b{y}_S<c$.

Wobec dowolności wyboru punktów $P$, $R$ i $S$ możemy zapisać, że współrzędne punktów leżących powyżej prostej $l$ spełniają nierówność

$ax+by>c$,

a współrzędne punktów leżących poniżej prostej l spełniają nierówność

$ax+by<c$.

Analogiczne rozumowanie należy przeprowadzić, gdy $a=0$ i $b\ne 0$.

Prosta $l$ przyjmuje wtedy postać

$by=c$

$y=\frac{c}{b}$

R1W2rNEkIi7qC

Ilustracja przedstawia wykres z poziomą osią $X$ oraz z pionową osią $Y$ bez podziałki. Na płaszczyźnie narysowano dwie proste. Pozioma narysowana jest linią ciągłą i opisuje ją wzór $l: by=c$. Prosta $l$ przechodzi przez pierwszą i drugą ćwiartkę układu. Druga, pionowa prosta, narysowana jest linią przerywaną i jest prostą pomocniczą poprowadzoną przez trzy zaznaczone na płaszczyźnie punkty. Prosta ta przechodzi przez pierwszą i czwartą ćwiartkę układu. Punkty zaznaczone na płaszczyźnie, które znajdują się pionowej prostej pomocniczej znajdują się w pierwszej ćwiartce i są to kolejno od góry: $R=\left(x_R;y_R\right), P=\left(x_P;y_P\right), S=\left(x_S;y_S\right)$, przy czym punkt $P$ należy również do prostej $l$.

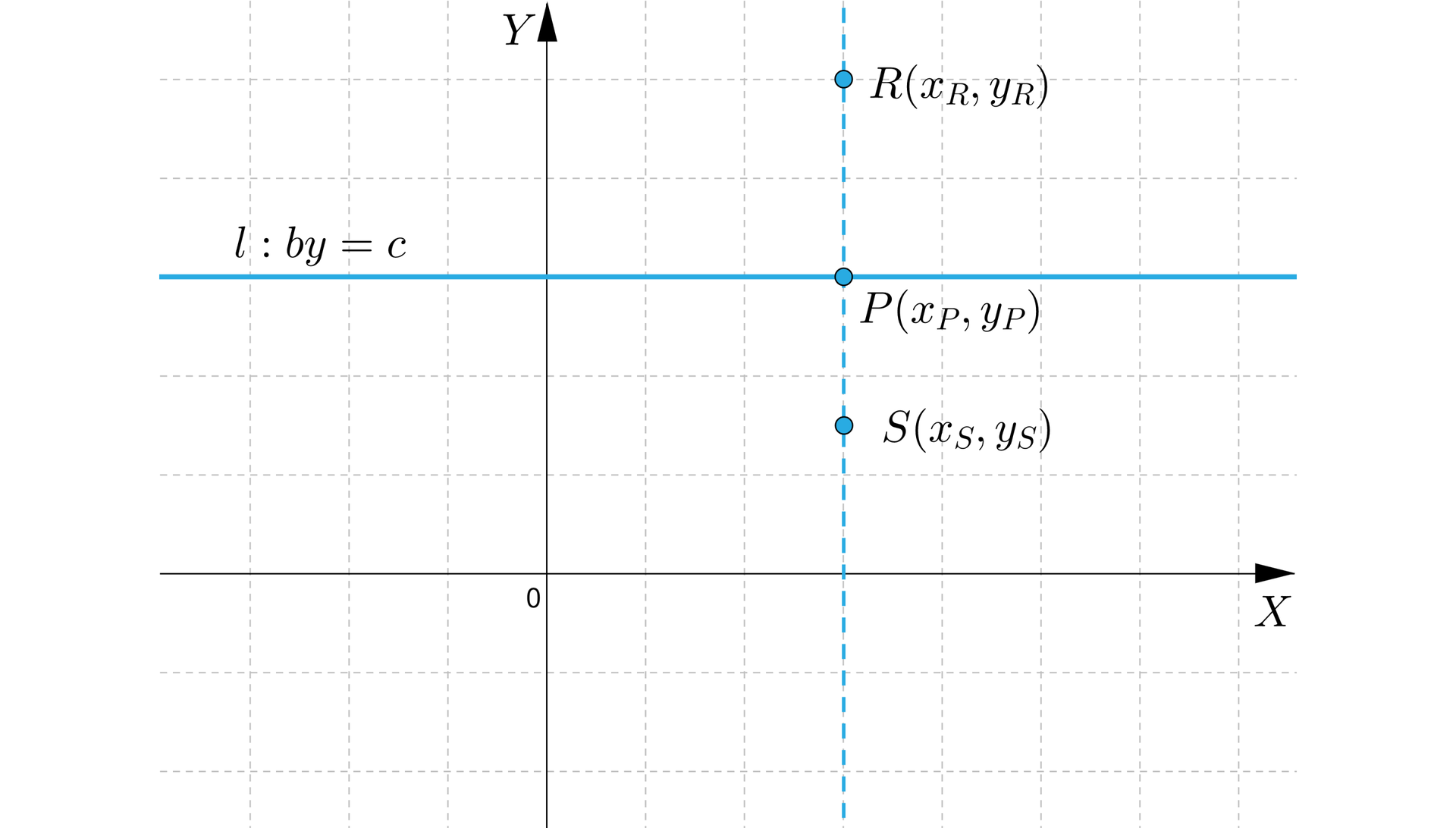
Rozpatrzmy przypadek, gdy $a\ne 0$ i $b=0$.

Wtedy prosta $l$ przyjmuje postać

$ax=c$

$x=\frac{c}{a}$

Zaznaczmy w układzie współrzędnych punkt $P$ leżący na tej prostej oraz punkty $R$ i $S$ leżące poza prostą, po przeciwnych jej stronach.

R17SdcFdzXaOj

Ilustracja przedstawia wykres z poziomą osią $X$ oraz z pionową osią $Y$ bez podziałki. Na płaszczyźnie narysowano linią ciągłą pionową prostą opisaną wzorem $x=\frac{c}{a}$. Na płaszczyźnie zaznaczono również trzy punkty leżące na tym samym poziomie. Punkt $S=\left(x_S;y_S\right)$ znajduje się w drugiej ćwiartce układu, a punkty $P=\left(x_P;y_P\right)$ oraz $R=\left(x_R;y_R\right)$ znajdują się w pierwszej ćwiartce ukłądu, przy czym punkt $P$ należy również do pionowej prostej.

Możemy zauważyć, że odcięta punktu $R$ spełnia warunek

$x_R>x=\frac{c}{a}$.

Więc

$x_R>\frac{c}{a}$

Stąd

$a{x}_R>c$.

W ten sam sposób możemy oszacować odciętą punktu $S$.

$x_S<x=\frac{c}{a}$.

Więc

$x_S<\frac{c}{a}$

Stąd

$a{x}_S<c$.

A zatem wobec dowolności wyboru punktów $P$, $R$ i $S$ otrzymujemy:

• współrzędne punktów leżących na lewo od prostej $l$ spełnią warunki
  $ax<c$, $y\in \mathrm{ℝ}$,

• współrzędne punktów leżących na prawo od prostej $l$ spełnią warunki
  $ax>c$, $y\in \mathrm{ℝ}$.

W prostokątnym ukladzie współrzędnych wykresem nierówności pierwszego stopnia z dwiema niewiadomymi jest jedna z półpłaszczyzn (z krawędzią, jeśli nierówność jest nieostra lub bez krawędzi, jeśli nierówność jest ostra), wyznaczona przez prostą $ax+by=c$.

zbiór wszystkich punktów, których współrzędne $\left(x,y\right)$ spełniają to równanie

prosta, będąca wykresem tego równania

nierówność postaci: