Przeczytaj
Definicja Cauchy'ego granicy funkcji w punkcie
Definicja Cauchy'ego granicy funkcji w punkcie jest definicją typowo arytmetyczną i wykorzystuje pojęcia otoczeniaotoczenia oraz sąsiedztwasąsiedztwa punktu. Spójrzmy, jak ona brzmi.
Liczbę nazywamy granicą funkcji : w punkcie , jeśli dla dowolnej liczby istnieje liczba taka, że dla każdego argumentu funkcji należącego do sąsiedztwa punktu o promieniu , wartość funkcji w tym argumencie należy do otoczenia liczby o promieniu .
Powyższą definicję można intuicyjnie rozumieć w następujący sposób: biorąc otoczenieotoczenie liczby rzeczywistej o dowolnym promieniu znajdziemy sąsiedztwosąsiedztwo punktu takie, że wartości funkcji w każdym argumencie należącym do znalezionego sąsiedztwa należeć będą do wziętego wcześniej otoczenia liczby . Na poniższym rysunku przedstawiona została interpretacja geometryczna definicji granicy funkcji w punkcie według Cauchy'ego.
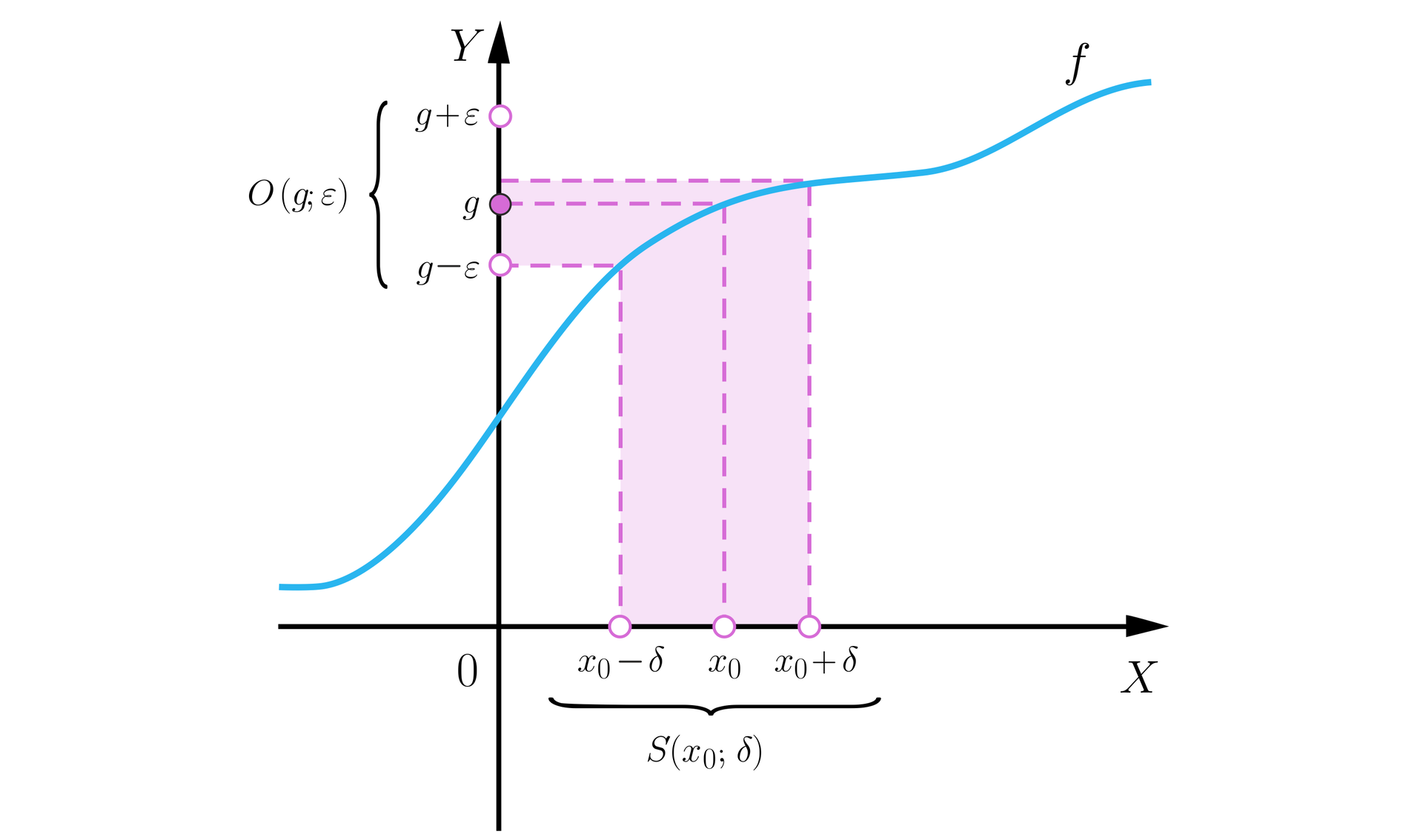
Jak korzystać z definicji Cauchy'ego granicy funkcji w punkcie?
Zaletą definicji Cauchy'ego granicy funkcji w punkcie jest fakt, że nie wykorzystuje ona innych pojęć matematycznych takich jak np. granica ciągu nieskończonego. Bazuje jedynie na zwykłej arytmetyce. Wadą jest jednak to, że korzystając z definicji Cauchy'ego na ogół nie jesteśmy w stanie obliczyć granicy funkcji w zadanym punkcie. Definicja służy przede wszystkim do wykazywania, że dana z góry liczba rzeczywista jest granicą funkcji w zadanym punkcie. Poniższe przykłady pokazują w jaki sposób możemy tego dokonać.
Wykażemy, że
Zgodnie z definicją Cauchy'ego bierzemy dowolną liczbę . Musimy wybrać liczbę rzeczywistą tak, aby dla wszystkich argumentów funkcji spełniających nierówności prawdziwa była nierówność . Spróbujmy przekształcić lewą stronę ostatniej nierówności podstawiając w miejsce wzór naszej funkcji
Otrzymany wynik sugeruje aby przyjąć , gdyż wówczas dla każdego takiego, że otrzymamy
co na mocy definicji Cauchy'ego dowodzi, że
Wykażemy, że
Weźmy dowolną liczbę . Dobierzemy liczbę tak, aby dla wszystkich argumentów funkcji spełniających nierówności prawdziwa była nierówność . Przekształćmy lewą stronę ostatniej nierówności.
Ponieważ wiemy, że więc . Jeśli zatem przyjmiemy , to otrzymamy
Z powyższego oraz z definicji Cauchy'ego granicy funkcji w punkcie wnioskujemy, że
Wykażemy, że
Weźmy dowolną liczbę . Dobierzemy liczbę tak, aby dla wszystkich argumentów funkcji spełniających nierówności prawdziwa była nierówność . Przekształćmy lewą stronę ostatniej nierówności.
Ponieważ więc . Jeśli zatem przyjmiemy , to otrzymamy
Z powyższego oraz z definicji Cauchy'ego granicy funkcji w punkcie wynika, że
Wykażemy, że
Weźmy dowolną liczbę . Dobierzemy liczbę tak, aby dla wszystkich argumentów funkcji spełniających nierówności prawdziwa była nierówność . Przekształćmy lewą stronę ostatniej nierówności.
Ponieważ więc podnosząc nierówność stronami do kwadratu oraz dodając stronami otrzymamy . Stąd
Zauważmy, że do wybranej wcześniej utalonej liczby musimy dobrać liczbę , tak aby . Chcemy zatem wybrać liczbę dodatnią tak aby spełniona była nierówność . Wybierając liczbę dodatnią dostatecznie bliską zeru, wyrażenie także przyjmie wartość na tyle bliską zeru aby spełniona była nierówność . Stąd, dla tak dobranej liczby z wcześniejszych obliczeń wynika, że dla wszystkich takich, że
Zatem udowodniliśmy, że
Związek definicji Cauchy'ego z definicją Heinego.
Okazuje się, że istnieje silny związek pomiędzy definicjami granicy funkcji w punkcie według Heinego oraz według Cauchy'ego. Mianowicie definicje te są równoważne. Mówi o tym poniższe twierdzenie.
Liczba jest granicą funkcji : w punkcie według Cauchy'ego wtedy i tylko wtedy, gdy jest ona granicą funkcji : w punkcie według Heinego.
Słownik
Otoczeniem punktu o promieniu nazywamy zbiór
Sąsiedztwo punktu o promieniu nazywamy zbiór