Przeczytaj

Jeżeli mówimy o monotoniczności funkcjimonotoniczność funkcjimonotoniczności funkcji, to określamy przedziały, w których funkcja jest rosnąca, malejąca, stała, niemalejąca lub nierosnąca.

Czasami mówimy, że określamy maksymalne przedziały, w których funkcja jest monotoniczna.

Mając daną parabolę, będącą wykresem funkcji kwadratowej możemy określić monotoniczność funkcjimonotoniczność funkcjimonotoniczność funkcji ze względu na to, jak skierowane są ramiona paraboli.

Jeżeli funkcja kwadratowa $f$ jest określona wzorem $f (x) = a x^{2} + b x + c$ , gdzie $a$ , $b$ , $c$ ∈ $ℝ$ oraz $a \neq 0$ , to współrzędne wierzchołka $W = (p, q)$ paraboli, która jest wykresem tej funkcji, obliczamy ze wzorów:

$p = \frac{- b}{2 a}$ , $q = \frac{- ∆}{4 a}$ , gdzie $∆ = b^{2} - 4 a c$ .

Do określenia maksymalnych przedziałów monotoniczności funkcji kwadratowej stosujemy następujące zależności:

dla $a > 0$ :

Ro7OLNqju3NdX

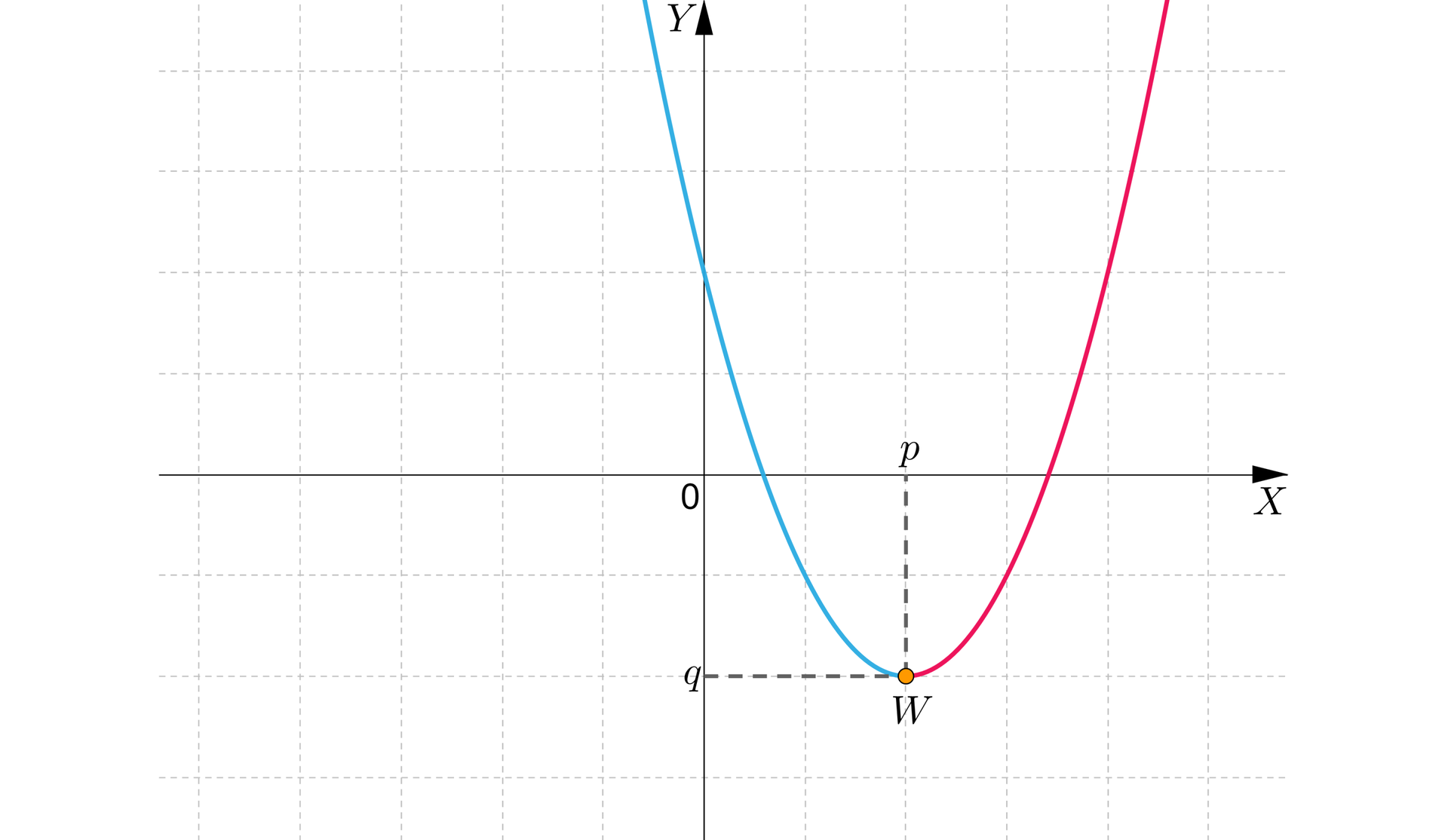
Ilustracja przedstawia układ współrzędnych z pionową osią Y i poziomą osią X. Zaznaczono parabolę z ramionami do góry z wierzchołkiem W o współrzędnych p;q

Funkcja jest:

- malejąca w przedziale $(- \infty, p⟩$ ,

- rosnąca w przedziale $⟨p, \infty)$ .

dla $a < 0$ :

Re2omjLzft9Xw

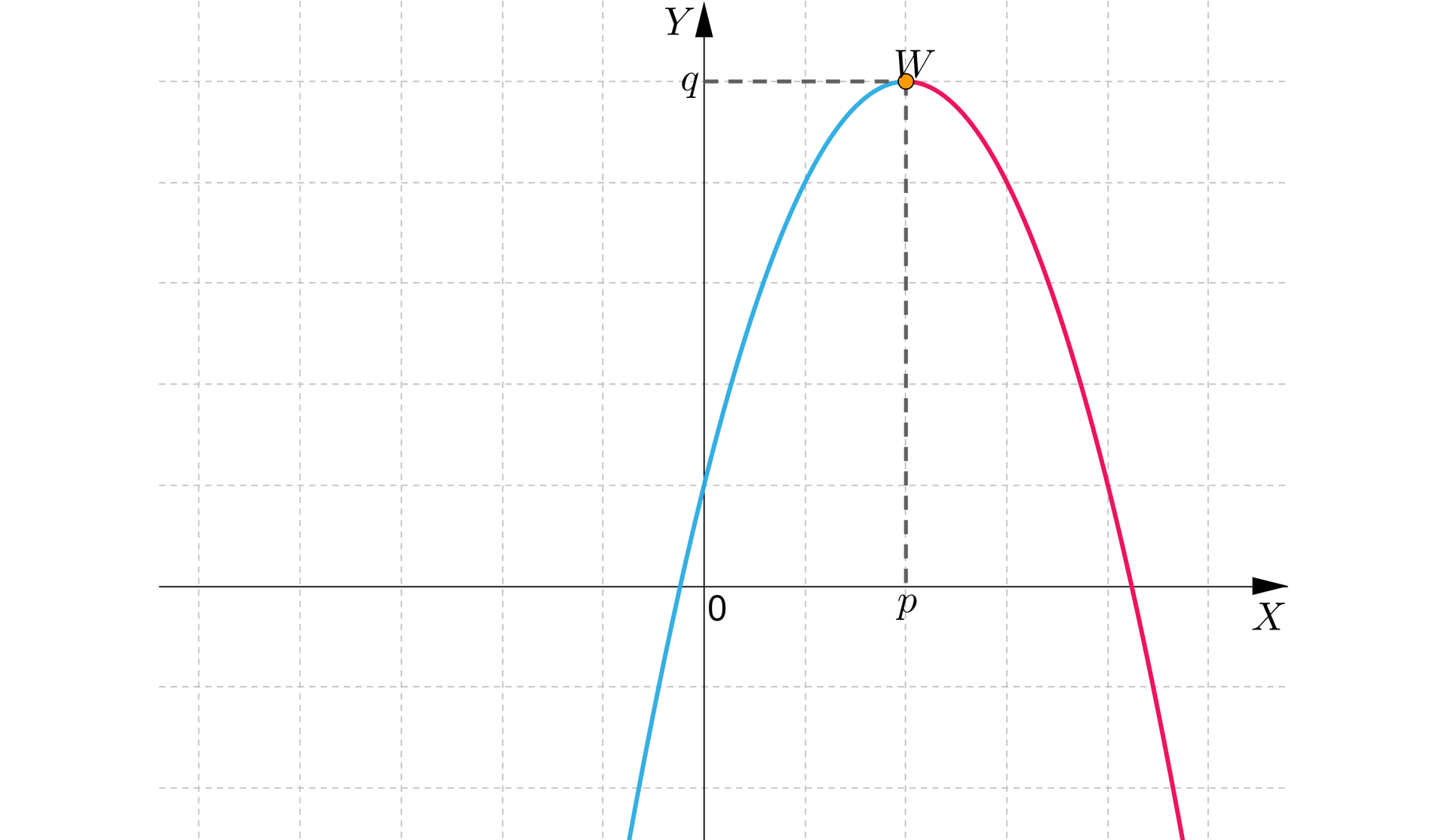
Ilustracja przedstawia układ współrzędnych z pionową osią Y i poziomą osią X. Zaznaczono parabolę z ramionami do dołu z wierzchołkiem W o współrzędnych p;q w pierwszej ćwiartce.

Funkcja jest:

- rosnąca w przedziale $(- \infty, p⟩$ ,

- malejąca w przedziale $⟨p, \infty)$ .

Wniosek:

Funkcja kwadratowafunkcja kwadratowaFunkcja kwadratowa nie jest monotoniczna w całej swojej dziedzinie, ale jest monotoniczna przedziałami.

Na przykład dla funkcji kwadratowej $f$ określonej wzorem $f (x) = 2 x^{2} - 1$ mamy:

$f (- 2) = 2 \cdot {(- 2)}^{2} - 1 = 7$

$f (0) = 2 \cdot 0^{2} - 1 = - 1$

$f (3) = 2 \cdot 3^{2} - 1 = 17$

Zauważmy, że $f (- 2) > f (0) < f (3)$ , zatem funkcja nie jest monotoniczna w całej swojej dziedzinie.

Przykład 1

Odczytamy maksymalne przedziały monotoniczności funkcji kwadratowej, której wykres przedstawiono na poniższym rysunku.

RZybMSgigv7M0

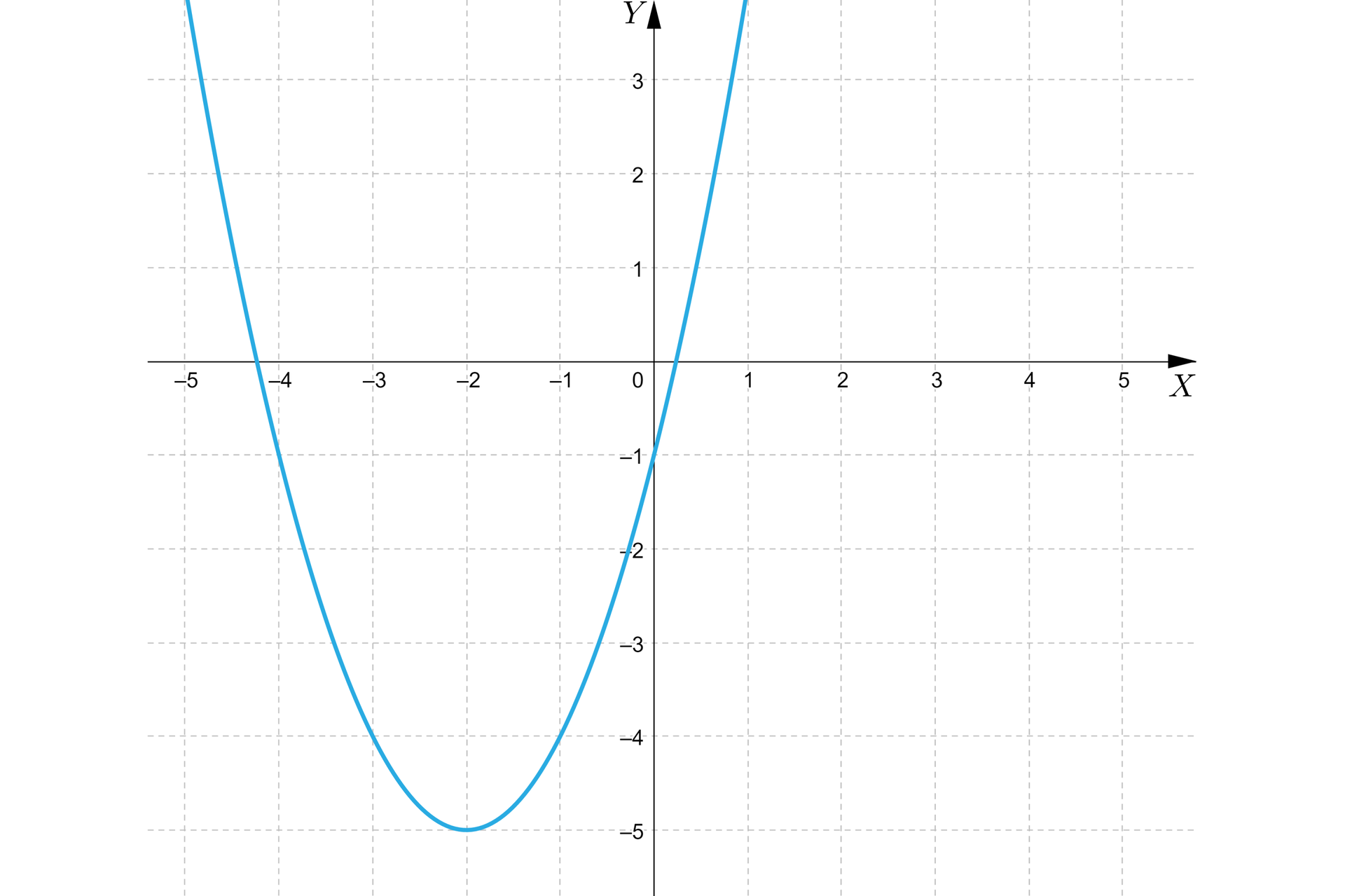
Ilustracja przedstawia układ współrzędnych z osią pionową od minus 5 do trzech oraz z osią poziomą od minus 5 do pięciu. Zaznaczono na nim parabolę z ramionami skierowanymi do góry oraz wierzchołkiem w punkcie -2;-5

Rozwiązanie:

Niech $W$ będzie wierzchołkiem paraboli, przedstawionej na rysunku. Zatem $W = (- 2, - 5)$ .

Wobec tego:

maksymalny przedział, w którym funkcja $f$ jest malejąca to $(- \infty, - 2⟩$ ,
maksymalny przedział, w którym funkcja $f$ jest rosnąca to $⟨- 2, \infty)$ .

Przykład 2

Wyznaczymy maksymalne przedziały monotoniczności funkcji kwadratowej $f$ określonej wzorem $f (x) = - 2 x^{2} + \frac{1}{3} x - 1$ .

Rozwiązanie:

W celu wyznaczenia maksymalnych przedziałów monotoniczności funkcji $f$ , obliczymy pierwszą współrzędną wierzchołka paraboli, która jest wykresem tej funkcji. Otrzymujemy:

$p = \frac{- \frac{1}{3}}{2 \cdot (- 2)} = \frac{1}{12}$ .

Ponieważ $a = - 2 < 0$ , więc ramiona paraboli są skierowane do dołu.

Zatem:

maksymalny przedział, w którym funkcja $f$ jest rosnąca to $(- \infty, \frac{1}{12}⟩$ ,
maksymalny przedział, w którym funkcja $f$ jest malejąca to $⟨\frac{1}{12}, \infty)$ .

Jeżeli funkcja kwadratowa $f$ jest zapisana za pomocą wzoru w postaci kanonicznej $f (x) = a {(x - p)}^{2} + q$ , to przedziały monotoniczności tej funkcji możemy określić na podstawie wartości współczynników $a$ oraz $p$ .

Przykład 3

Wyznaczymy maksymalne przedziały monotoniczności funkcji $f$ określonej wzorem $f (x) = - {(x + 4)}^{2} - 3$ .

Rozwiązanie:

Ze wzoru funkcji odczytujemy, że $a = - 1$ oraz $p = - 4$ .

Ponieważ $a < 0$ , zatem:

maksymalny przedział, w którym funkcja $f$ jest rosnąca to $(- \infty, - 4⟩$ ,
maksymalny przedział, w którym funkcja $f$ jest malejąca to $⟨- 4, \infty)$ .

Jeżeli znamy maksymalny przedział, w którym funkcja kwadratowa jest rosnąca lub malejąca, to możemy wyznaczyć wartości współczynników we wzorze tej funkcji.

Przykład 4

Dana jest funkcja kwadratowa $f$ określona wzorem $f (x) = \frac{1}{3} x^{2} + b x + 1$ . Wyznaczymy wartość współczynnika $b$ , jeżeli wiadomo, że maksymalny przedział, w którym funkcja jest rosnąca to $⟨3, \infty)$ .

Rozwiązanie:

Ponieważ maksymalny przedział, w którym funkcja $f$ jest rosnąca to $⟨3, \infty)$ , zatem pierwsza współrzędna wierzchołka $p$ paraboli, będącej wykresem funkcji kwadratowej wynosi $p = 3$ .

Jeżeli wykorzystamy wzór na $p$ , to otrzymujemy równanie na współczynnik $b$ :

$3 = \frac{- b}{2 \cdot \frac{1}{3}}$ , zatem $b = - 2$ .

Przykład 5

Wyznaczymy wartości współczynników $a$ i $b$ we wzorze funkcji kwadratowej $f (x) = a x^{2} + b x - 1$ , jeżeli wiadomo, że maksymalny przedział, w którym funkcja jest malejąca to $(- \infty, - 2⟩$ oraz do wykresu tej funkcji należy punkt o współrzędnych $(2, 2)$ .

Rozwiązanie:

Ponieważ maksymalny przedział, w którym funkcja jest malejąca to $(- \infty, - 2⟩$ , zatem $p = - 2$ , czyli $- 2 = \frac{- b}{2 a}$ .

Ponieważ punkt o współrzędnych $(2, 2)$ należy do wykresu tej funkcji, zatem: $2 = a \cdot 2^{2} + b \cdot 2 - 1$ .

Otrzymujemy układ równań:

$\{\begin{cases} - 2 = \frac{- b}{2 a} \\ 2 = 4 a + 2 b - 1 \end{cases}$

Pierwsze równanie przekształcamy do postaci $b = 4 a$ , a po podstawieniu do drugiego równania, otrzymujemy równanie, z którego wyznaczymy wartość współczynnika $a$ :

$2 = 4 a + 8 a - 1$ , czyli $a = \frac{1}{4}$ .

Zatem $b = 4 \cdot \frac{1}{4} = 1$ .

Monotoniczność funkcji kwadratowej możemy określać także korzystając z definicji funkcji monotonicznej.

Przykład 6

Wykażemy, że funkcja kwadratowa $f$ określona wzorem $f (x) = \sqrt{3} x^{2} - 3$ jest malejąca w przedziale $(- \infty, 0 ⟩$ .

Rozwiązanie:

Niech $x_{1}, x_{2} \in (- \infty, 0 ⟩$ oraz $x_{1} < x_{2}$ .

Wówczas:

$f (x_{1}) = \sqrt{3} \cdot {x_{1}}^{2} - 3$

$f (x_{2}) = \sqrt{3} \cdot {x_{2}}^{2} - 3$

$f (x_{2}) - f (x_{1}) = \sqrt{3} \cdot {x_{2}}^{2} - 3 - (\sqrt{3} \cdot {x_{1}}^{2} - 3) =$

$= \sqrt{3} \cdot {x_{2}}^{2} - 3 - \sqrt{3} \cdot {x_{1}}^{2} + 3 = \sqrt{3} \cdot {x_{2}}^{2} - \sqrt{3} \cdot {x_{1}}^{2} =$

$= \sqrt{3} \cdot (x_{2} - x_{1}) \cdot (x_{1} + x_{2})$

Zauważmy, że $\sqrt{3} \cdot (x_{2} - x_{1}) \cdot (x_{1} + x_{2}) < 0$ , zatem $f (x_{1}) > f (x_{2})$ .

Stąd wobec dowolności $x_{1}$ oraz $x_{2}$ wnioskujemy, że funkcja $f$ jest malejąca w przedziale $(- \infty, 0 ⟩$ .

Przykład 7

Wyznaczymy, dla jakich wartości parametru $m$ , gdzie $m \in ℝ$ , funkcja kwadratowa $f$ określona wzorem $f (x) = - x^{2} + m x - 2$ jest rosnąca w przedziale $(- \infty, m^{2} - 3 m + 1 ⟩$ .

Rozwiązanie:

Obliczamy wartość $p$ pierwszej współrzędnej wierzchołka paraboli, będącej wykresem funkcji $f$ :

$p = \frac{- m}{2 \cdot (- 1)} = \frac{m}{2}$

Jeżeli funkcja kwadratowa $f$ jest rosnąca w przedziale $(- \infty, m^{2} - 3 m + 1 ⟩$ , to do wyznaczenia wartości parametru $m$ rozwiązujemy nierówność:

$\frac{m}{2} \geq m^{2} - 3 m + 1$

Nierówność przekształcamy do postaci:

$2 m^{2} - 7 m + 2 \leq 0$

Obliczamy $m_{1} = \frac{7 - \sqrt{33}}{4}$ oraz $m_{2} = \frac{7 + \sqrt{33}}{4}$ .

Rozwiązaniem nierównocści jest zbiór liczb $m \in ⟨ \frac{7 - \sqrt{33}}{4}, \frac{7 + \sqrt{33}}{4} ⟩$ .

Zatem funkcja $f$ jest rosnąca w przedziale $(- \infty, m^{2} - 3 m + 1 ⟩$ , gdy $m \in ⟨ \frac{7 - \sqrt{33}}{4}, \frac{7 + \sqrt{33}}{4} ⟩$ .

Słownik

monotoniczność funkcji

własność funkcji, która określa zmianę wartości tej funkcji wraz ze wzrostem argumentów

funkcja kwadratowa

funkcja określona na zbiorze $ℝ$ wzorem $f (x) = a x^{2} + b x + c$ , gdzie $a$ , $b$ , $c$ ∈ $ℝ$ oraz $a \neq 0$

Wprowadzenie

Schemat interaktywny

Słownik