Schemat interaktywny
Polecenie 1
Przeanalizuj działanie schematu interaktywnego, dotyczącego wyznaczania przedziałów monotoniczności funkcji kwadratowej określonej wzorem w postaci ogólnej, a następnie wykonaj poniższe polecenia.
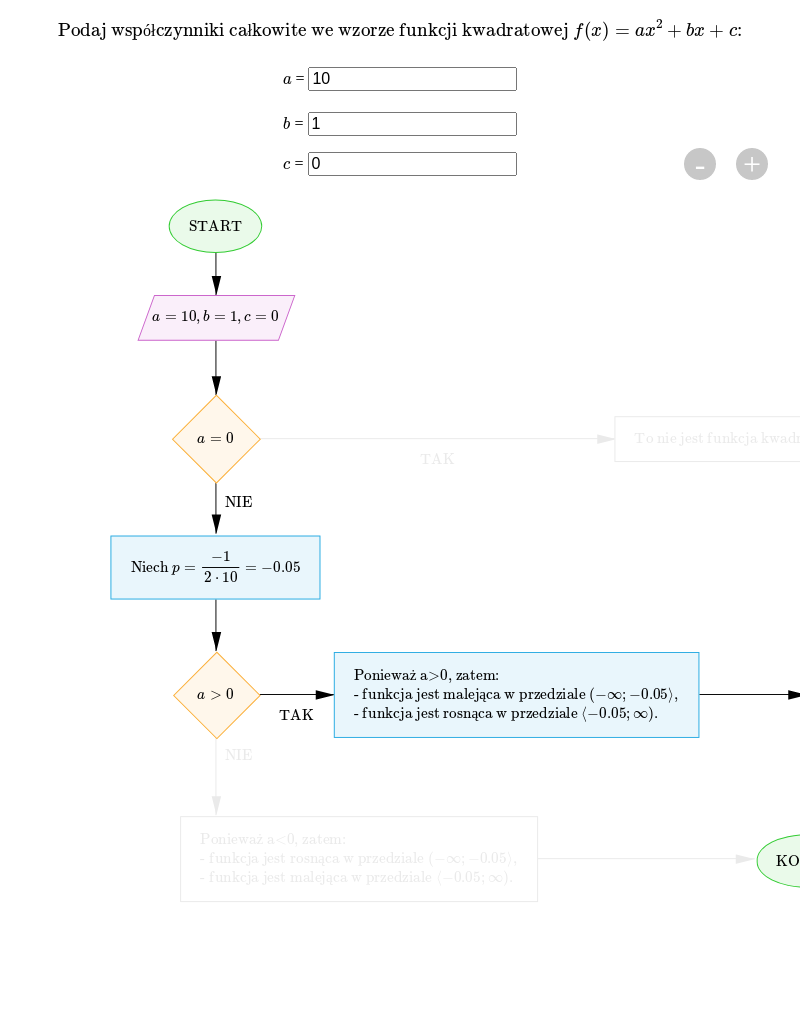
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DMGYyC4tI
Polecenie 2
Wyznacz maksymalne przedziały monotoniczności funkcji :
a) określonej za pomocą wzoru ,
b) jeżeli jej wykres przedstawiono na poniższym rysunku.
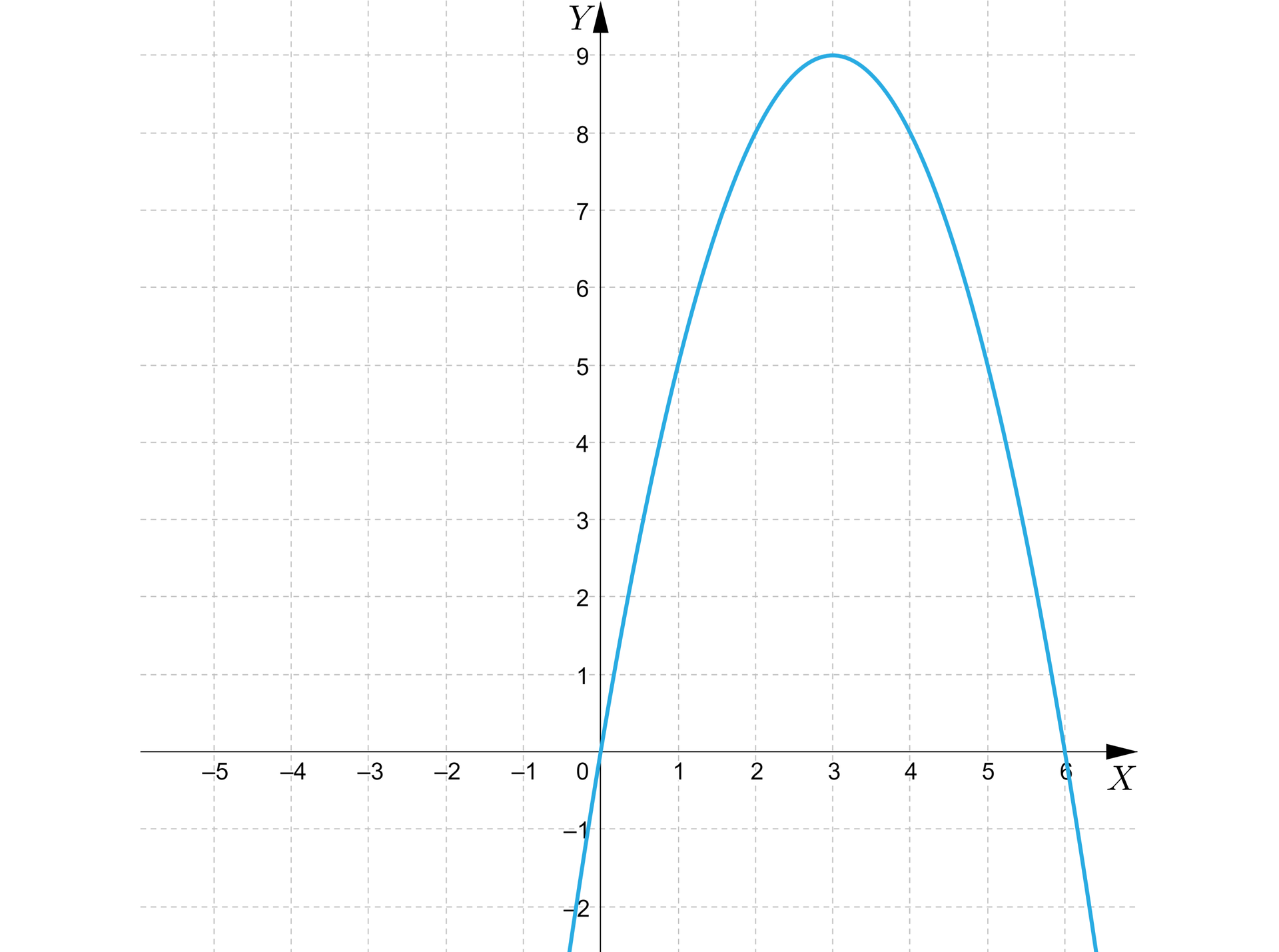
Polecenie 3
W poniższym schemacie przygotuj algorytm określający monotoniczność funkcji kwadratowej na podstawie jej wzoru .
Przygotuj w języku Python algorytm określający monotoniczność funkcji kwadratowej na podstawie jej wzoru .