Przeczytaj

Prześledźmy kilka przykładów dotyczących okręgów lub kół, w których wykorzystamy twierdzenie Pitagorasa.

Przykład 1

W okręgu o promieniu $17$ poprowadzono cięciwę, która jest oddalona od środka tego okręgu o $8$ . Oblicz jej długość.

Rozwiązanie

Przyjmijmy oznaczenia, jak na rysunku.

R1exlfGXR7Cq5

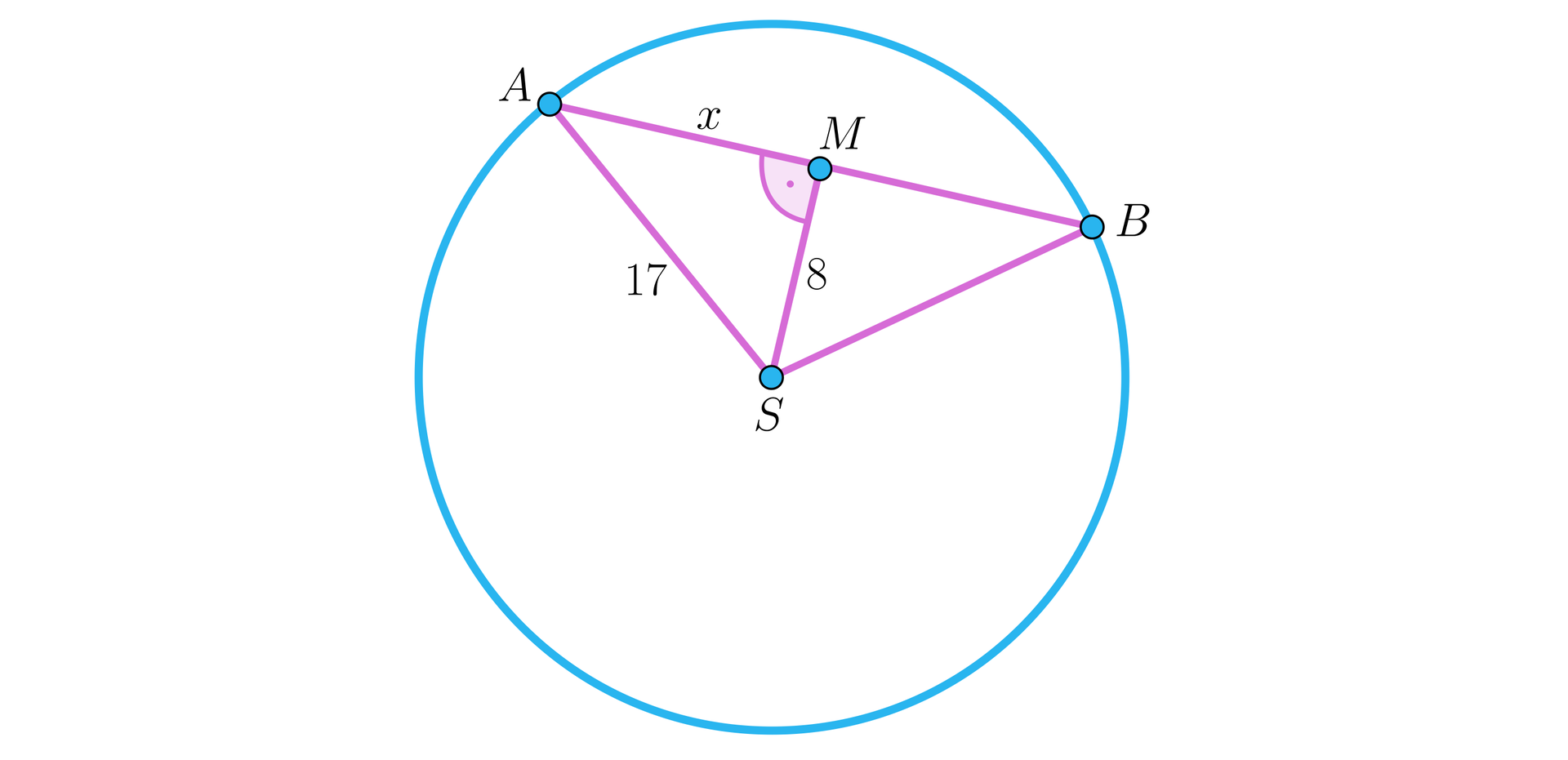
Na ilustracji przedstawiono okrąg o środku w punkcie S. Na okręgu zaznaczono cięciwę AB, na której leży punkt M. Odległość punktu M od S wynosi osiem. Długość odcinka AM jest równa x. Długość odcinka AS jest równa siedemnaście.

Odległość środka $S$ okręgu od cięciwy $A B$ to długość najkrótszego odcinka, którego jednym końcem jest punkt $S$ , a drugim - punkt leżący na cięciwie $A B$ . Jak wiemy, odległość punktu $S$ od prostej to długość odcinka $S M$ prostopadłego do tej prostej, którego koniec $M$ leży na tej prostej. Ponieważ odcinki $A S$ i $B S$ są promieniami okręgu, to trójkąt $A B S$ jest równoramienny. Oczywiście, o ile cięciwa nie jest średnicą okręgu. Zatem najkrótszy z odcinków łączący środek $S$ z cięciwą $A B$ to wysokość $S M$ trójkąta $A B S$ . Spodek $M$ tej wysokości jest zatem środkiem cięciwy $A B$ .

Z twierdzenia Pitagorasa w trójkącie $A S M$ otrzymujemy ${|A S|}^{2} = {|A M|}^{2} + {|S M|}^{2}$ ,

czyli $17^{2} = x^{2} + 8^{2}$ .

Stąd $x = \sqrt{17^{2} - 8^{2}} = 15$ . Zatem $|A B| = 2 x = 30$ .

Przykład 2

Punkt $C$ leży na cięciwie $A B$ okręgu o środku $S$ . Długości odcinków $A C$ , $B C$ i $S C$ są równe: $|A C| = 4$ , $|B C| = 10$ i $|S C| = 5$ . Oblicz promień tego okręgu.

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku.

R1GcqSXhDTxcw

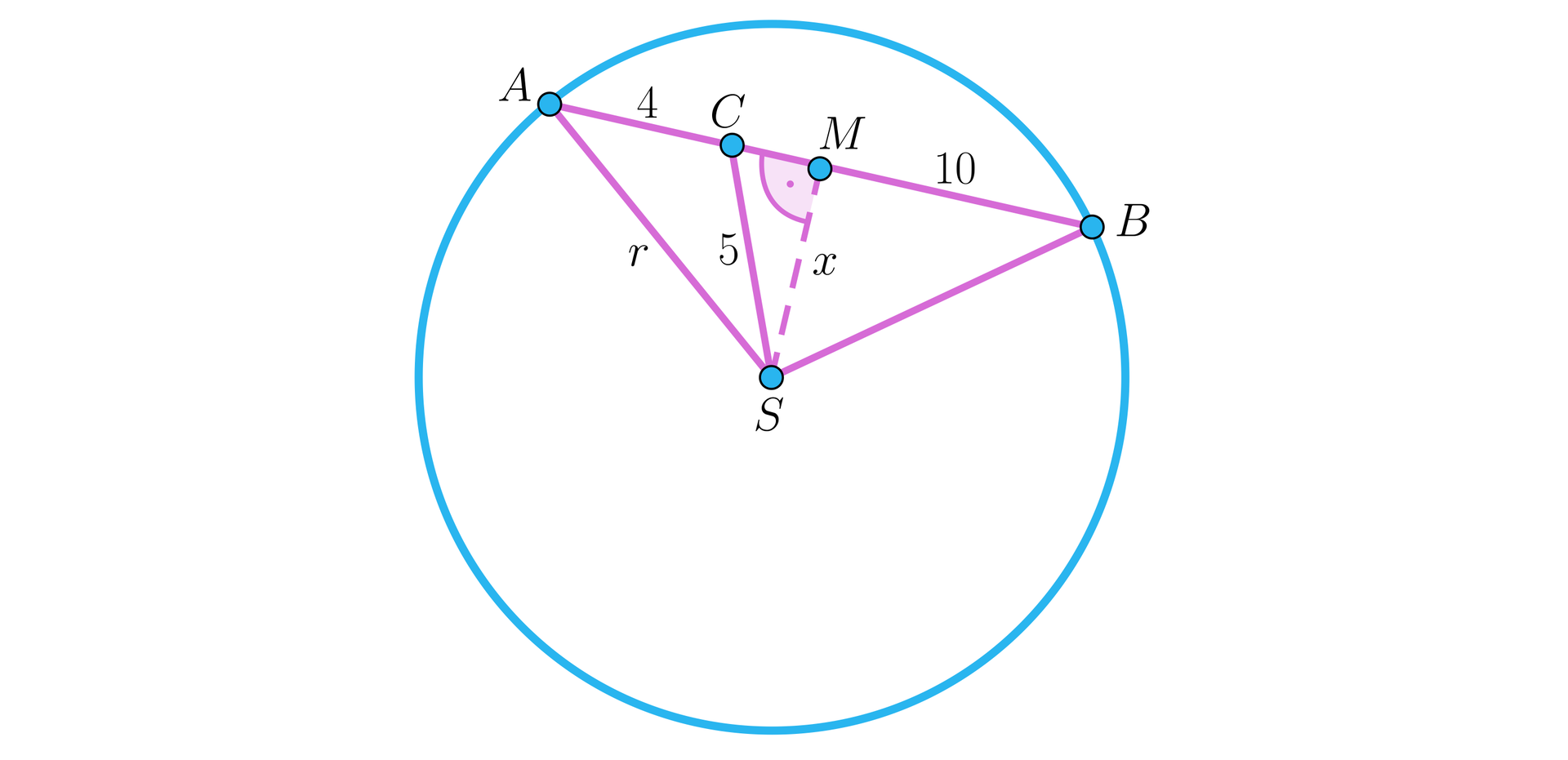
Na ilustracji przedstawiono okrąg o środku w punkcie S. Na okręgu zaznaczono cięciwę AB, na której leży punkt M. Punkt M leży w odległości 10 od punktu B. Odległość punktu M od S oznaczono literą x. Na odcinku AM zaznaczono punkt C. Powstał trójkąt ACS, którego bok AC jest równy 4, bok CS jest równy 5, natomiast AS oznaczono r. Długość odcinka AS jest równa siedemnaście.

Poprowadźmy odcinek $S M$ , gdzie $M$ to środek cięciwy $A B$ . Niech $r = |S A|$ oraz $x = |S M|$ . Wtedy $|A M| = |B M| = \frac{4 + 10}{2} = 7$ , więc $|C M| = 7 - 4 = 3$ .

Z twierdzenia Pitagorasa dla trójkąta $C M S$ otrzymujemy ${|C S|}^{2} = {|C M|}^{2} + {|S M|}^{2}$ , czyli $5^{2} = 3^{2} + x^{2}$ .

Stąd $x = \sqrt{5^{2} - 3^{2}} = 4$ .

Ponownie korzystając z twierdzenia Pitagorasa, ale tym razem dla trójkąta $A M S$ mamy ${|A S|}^{2} = {|A M|}^{2} + {|S M|}^{2}$ ,

czyli $r^{2} = 7^{2} + 4^{2}$ .

Stąd $r = \sqrt{7^{2} + 4^{2}} = \sqrt{65}$ .

Przykład 3

W okręgu o środku $S$ i promieniu $r$ poprowadzono dwie prostopadłe cięciwy $A B$ i $C D$ o długościach $|A B| = a$ i $|C D| = b$ , przecinające się w punkcie $P$ . Odległość między punktami $S$ i $P$ jest równa $|S P| = d$ . Udowodnij, że $r = \sqrt{\frac{a^{2} + b^{2} + 4 d^{2}}{8}}$ .

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku.

RDaeDVBvEso91

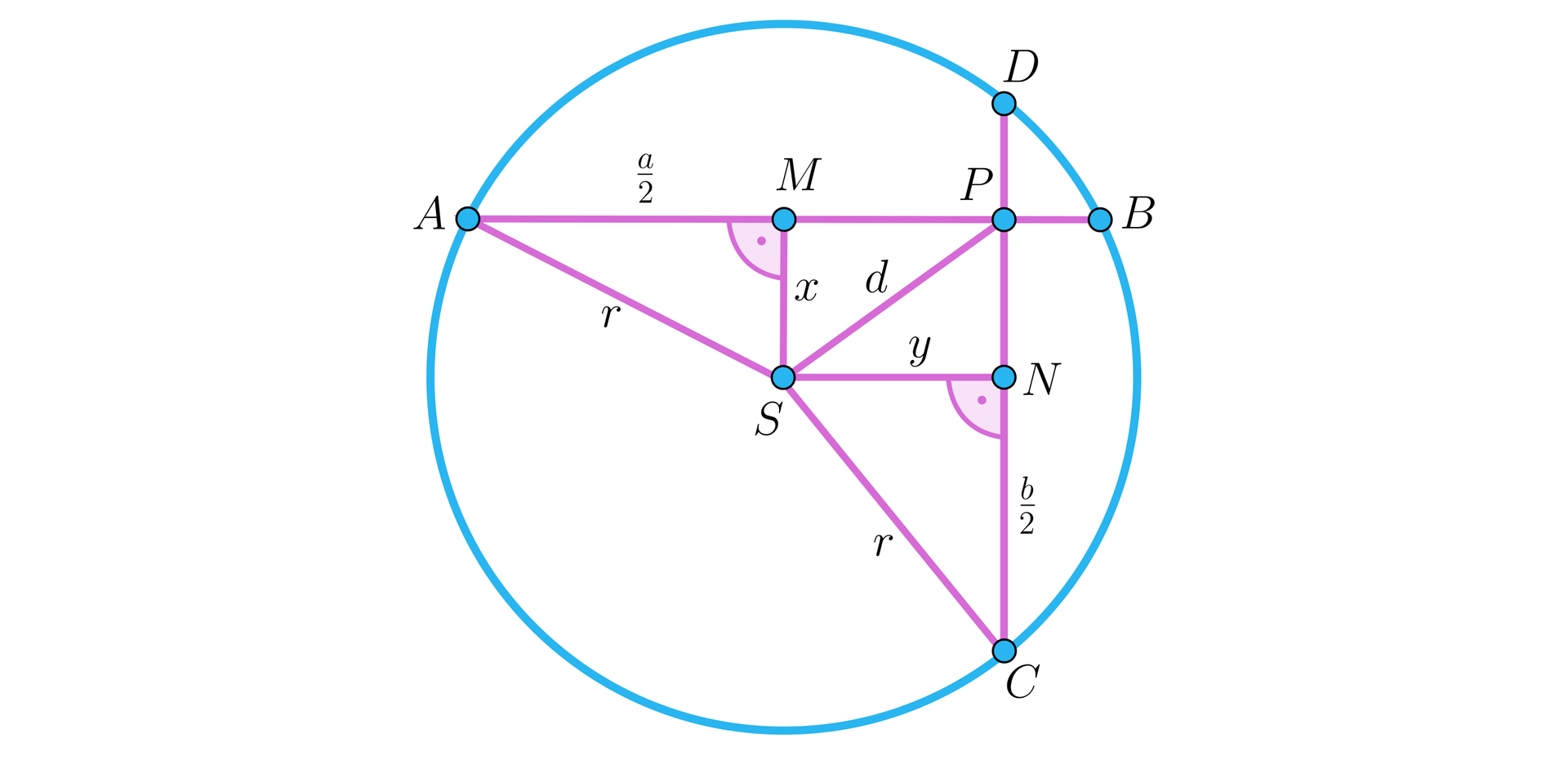
Na ilustracji przedstawiono okrąg o środku w punkcie S. Zaznaczono cięciwę AB, na której zaznaczono, kolejno od lewej punkt M i P. Punkt M leży prostopadle do punktu S, w odległości równej x. Długość odcinka AM oznaczono a2, natomiast długość odcinka AS oznaczono r. Z punktu P poprowadzono prostą do obwiedni okręgu w punkcie D. Zaznaczono punkt N, taki że powstał prostokąt MPNS o długości boku MS równym x, boku SN równym y, oraz przekątnej równej d. Ze środka okręgu S poprowadzono promień okręgu do punktu C. Zaznaczono trójkąt CNS z kątem prostym przy wierzchołku N, którego bok CN wynosi b2, oraz CS wynosi r.

Z twierdzenia Pitagorasatwierdzenie Pitagorasatwierdzenia Pitagorasa dla trójkąta $A M S$ otrzymujemy ${|A S|}^{2} = {|A M|}^{2} + {|S M|}^{2}$ , czyli $r^{2} = {(\frac{a}{2})}^{2} + x^{2}$ .

Stąd $x^{2} = r^{2} - \frac{a^{2}}{4}$ .

Tak samo z twierdzenia Pitagorasa dla dla trójkąta $C N S$ otrzymujemy ${|C S|}^{2} = {|C N|}^{2} + {|S N|}^{2}$ , czyli $r^{2} = {(\frac{b}{2})}^{2} + y^{2}$ . Stąd $y^{2} = r^{2} - \frac{b^{2}}{4}$ .

Ponownie wykorzystamy twierdzenie Pitagorasa dla trójkąta $S M P$ . Dostajemy wtedy ${|S P|}^{2} = {|S M|}^{2} + {|M P|}^{2}$ , czyli $d^{2} = x^{2} + y^{2}$ .

Stąd i z otrzymanych poprzednio dwóch równości mamy $d^{2} = r^{2} - \frac{a^{2}}{4} + r^{2} - \frac{b^{2}}{4}$ , skąd otrzymujemy kolejno $2 r^{2} = d^{2} + \frac{a^{2}}{4} + \frac{b^{2}}{4}$ , $r^{2} = \frac{4 d^{2} + a^{2} + b^{2}}{8}$ .

Zatem $r = \sqrt{\frac{4 d^{2} + a^{2} + b^{2}}{8}}$ . To należało udowodnić.

Przykład 4

Pokażemy, że mając do dyspozycji dwa kije, każdy o długości $1,7 m$ możemy tak je ułożyć na okrągłej cembrowinie studnicembrowina studnicembrowinie studni o średnicy $2 m$ , żeby można było do któregoś z tych kijów przywiązać obciążony sznur, który będzie wskazywał środek okręgu cembrowiny.

Rozwiązanie

Zanim sporządzimy rysunek, zauważmy, że skoro obciążony sznur ma wskazywać środek okręgu cembrowiny studni, to musi on być przywiązany do któregoś kija w punkcie leżącym dokładnie w środku okręgu. Wobec tego kij ten musi być ułożony wzdłuż średnicy studni. Ponieważ jednak jego długość jest mniejsza od średnicy studni, to nie może on opierać się na cembrowinie dwoma końcami. Stąd wniosek, że jednym końcem musi opierać się na drugim kiju, który z kolei musi obydwoma końcami opierać się na cembrowinie. Teraz możemy więc sporządzić odpowiedni rysunek.

R9zCvraL41iOV

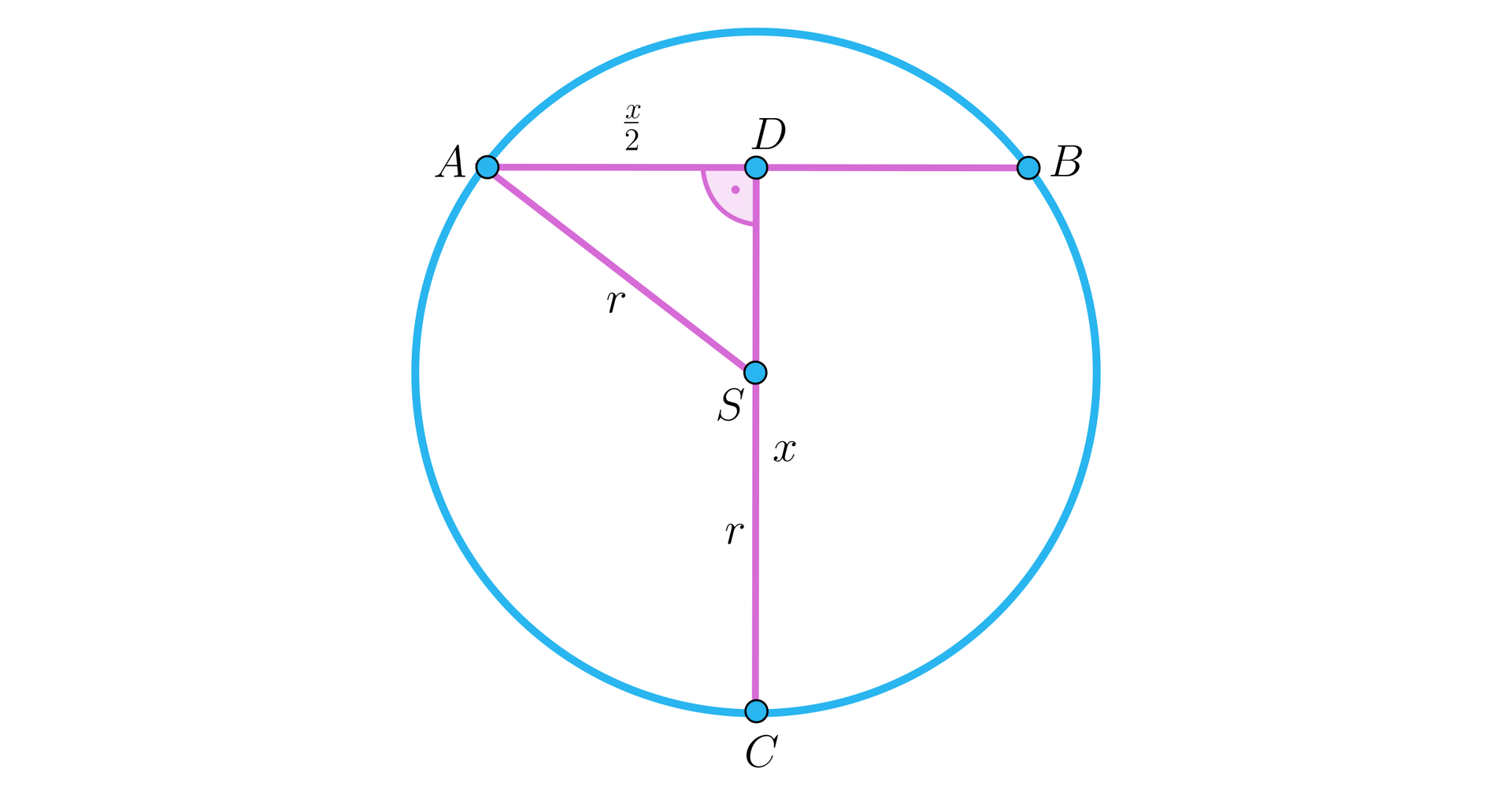
Na ilustracji przedstawiono okrąg o środku w punkcie S. Zaznaczono poziomą cięciwę AB, na której zaznaczono punkt D leżący prostopadle do środka okręgu. Zaznaczono trójkąt ADS, z kątem prostym przy wierzchołku D. Długość przyprostokątnej AD wynosi x2, natomiast przeciwprostokątna AS stanowi promień r okręgu. Zaznaczono odcinek SC, stanowiący promień okręgu, leżący na przedłużeniu przyprostokątnej DS. Odcinek DC oznaczono x.

Połóżmy kije tak, żeby kij $A B$ był prostopadły do kija $C D$ . Minimalną długość kija oznaczmy przez $x$ , a więc $|A B| = |C D| = x$ , a przez $r$ - promień okręgu.

Wówczas przyprostokątna $D S$ trójkąta prostokątnego $A D S$ ma długość równą $|D S| = x - r$ .

Z twierdzenia Pitagorasa otrzymujemy ${|A S|}^{2} = {|A D|}^{2} + {|D S|}^{2}$ , czyli $r^{2} = {(\frac{x}{2})}^{2} + {(x - r)}^{2}$ .

Stąd $r^{2} = \frac{x^{2}}{4} + x^{2} - 2 r x + r^{2}$ , a dalej $\frac{5 x^{2}}{4} = 2 r x$ , czyli $x = \frac{8}{5} r$ .

Zatem $x = \frac{4}{5} \cdot 2 r$ . To oznacza, że kij musi mieć długość co najmniej równą $\frac{4}{5}$ długości średnicy.

Jeśli więc średnica cembrowiny jest równa $2 m$ , to długość kija musi być równa co najmniej $\frac{4}{5} \cdot 2 = 1, 6 m$ . Kij o długości $1,7 m$ spełnia ten warunek.

Słownik

twierdzenie Pitagorasa

Jeżeli $a$ i $b$ są długościami przyprostokątnych, zaś $c$ długością przeciwprostokątnej w trójkącie prostokątnym, to zachodzi związek $a^{2} + b^{2} = c^{2}$ .

cembrowina studni

betonowy krąg uniemożliwiający osuwanie się ziemi do otworu studni

Wprowadzenie

Animacja

Słownik