Przeczytaj
Przeprowadzenie dowodu matematycznego polega na wykazaniu, że pewne zdanie jest prawdziwe. Każdy krok dowodu musi jasno wynikać z poprzednich lub być przyjętym aksjomatem, czyli faktem matematycznym, którego prawdziwość jest ogólnie znana, przyjmowanym bez dowodu. Ostatni krok dowodu to udowodnione zdanie, które w ten sposób staje się twierdzeniem. Do udowodnienia nowych twierdzeń można użyć wcześniej udowodnionych; można też odwołać się do aksjomatówaksjomatów, które są punktem wyjścia, „regułami” akceptowanymi przez wszystkich. Dowód matematyczny jest absolutny, co oznacza, że raz udowodnione twierdzenie zostaje udowodnione na zawsze. Dopóki jednak nie zostanie udowodnione, dane stwierdzenie nigdy nie jest akceptowane jako prawdziwe.
Istnieje wiele technik, których można użyć do udowodnienia twierdzeń. Nie ma jednego idealnego wzorca dowodudowodu – twierdzenie można udowodnić za pomocą różnych technik i żadna z nich nie będzie lepsza ani gorsza (o ile wszystkie są prawidłowe). Na przykład w słynnym opracowaniu „Dowody z księgi” możemy znaleźć sześć różnych dowodów na nieskończoność zbioru liczb pierwszych.
Pomimo tego, że będziemy używać praktycznie tylko dwóch metod dowodzenia twierdzeń, warto wiedzieć, że istnieje ich sporo, np.:
dowód wprost,
dowód nie wprost,
dowód kombinatoryczny,
dowód indukcyjny,
dowód geometryczny.
W tym materiale zajmiemy się najbardziej popularny rodzajem dowodu – dowodem wprostdowodem wprost.
Dowodząc twierdzenie, zapisane w postaci implikacji, metodą wprost przyjmujemy wszystkie założenia (czyli poprzednik implikacji jest prawdziwy) i rozumujemy do momentu gdy stwierdzimy, że teza jest poprawna (następnik implikacji jest prawdziwy).
Zapamiętaj: Sprawdzenie prawdziwości twierdzenia w kilku konkretnych przypadkach (np. dla konkretnych liczb) nie stanowi dowodu. Twierdzenie uważamy za udowodnione jeśli całe rozumowanie zostało przeprowadzone na symbolach ogólnych.
Wykażemy, że różnica kwadratów dwóch kolejnych liczb parzystych naturalnych dodatnich jest liczbą podzielną przez .
Rozwiązanie
Założenie: i to dwie liczby naturalne dodatnie parzyste (przy czy możemy założyć, że jest większą z tych liczb).
Teza: .
Dowód:
Jeśli jest liczbą naturalną parzystą, to kolejną liczbą parzystą jest .
Wówczas różnicę kwadratów tych liczb możemy zapisać:
,
gdzie jest liczbą naturalną.
Tak więc różnica kwadratów dwóch kolejnych liczb parzystych jest wielokrotnością liczby , czyli jest podzielna przez .
c.n.d. (co należało dowieść)
Poniższy przykład dotyczy wykorzystania znanych już twierdzeń do udowodnienia nowego twierdzenia.
Dany jest czworokąt wypukły niebędący równoległobokiem. Punkty , są odpowiednio środkami boków i . Punkty , są odpowiednio środkami przekątnych i . Uzasadnij, że .
Rozwiązanie
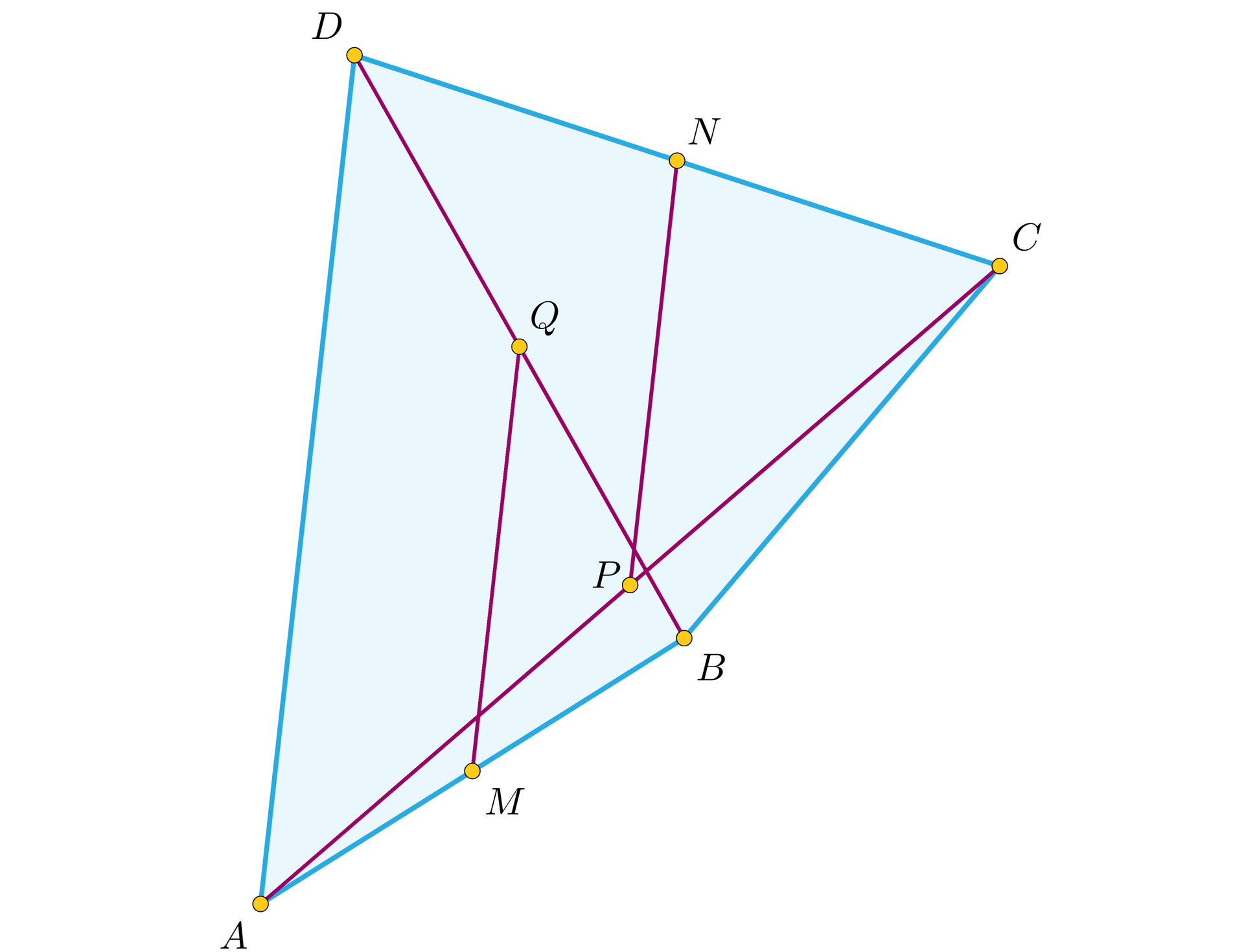
Założenie: Czworokąt jest wypukły; czworokąt nie jest równoległobokiem; ; ; ; .
Teza: .
Dowód:
Z zastosowania do trójkąta twierdzenia o odcinku łączącym środki boków w trójkącie mamy: .
Z zastosowania tego samego twierdzenia do trójkąta mamy: .
Stąd: .
c.n.d.
Uwaga 1
Założenie, że czworokąt nie jest równoległobokiem, jest tutaj bardzo ważne. Poniżej w aplecie możemy zmieniać położenie wierzchołków czworokąta i zobaczyć, co się dzieje z badanymi odcinkami, gdy „staje się” równoległobokiem.
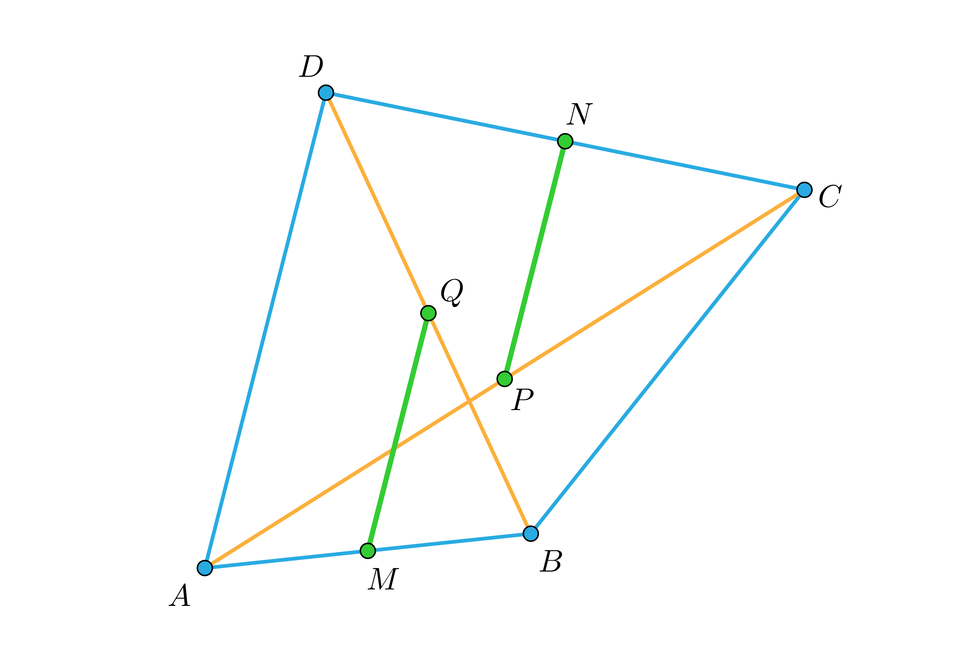
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DuZumfDTX
Powyżej celowo nie pokazano „pełnego” równoległoboku. Do jakiego wzajemnego położenia dążą nasze badane odcinki, gdy czworokąt „dąży” do równoległoboku?
Odpowiedź: Do położenia na jednej prostej.
Uwaga 2
Na rysunku pomocniczym nasze rozważane odcinki zostały zmierzone. Jak – pod wpływem tej obserwacji – można rozszerzyć nasze twierdzenie?
Odpowiedź: Można zapisać tezę w postaci: Uzasadnij, że odcinki i są równoległe i równe.
A tutaj mamy przykład dowodu, w którym na początku wykorzystujemy dobrze znane fakty matematyczne.
Udowodnimy, że dla każdej liczby rzeczywistej i każdej liczby rzeczywistej prawdziwa jest nierówność:
.
Rozwiązanie:
Założenie: i to liczby rzeczywiste.
Teza: .
Dowód:
Na początku dowodu prawdopodobnie wiele osób stwierdzi, że nie wiadomo, jak skorzystać z założenia; nie widzimy żadnej zależności pomiędzy i , którą moglibyśmy zacząć przekształcać, aby dojść do tezy. W takiej sytuacji dobrze jest skorzystać z jakichś zależności, o których wiemy, że są na pewno prawdziwe. W tym przypadku niech to będą następujące zależności:
, , .
Dlaczego właśnie te? Między innymi dlatego, że w tezie występują m.in. jednomiany , i , a te łatwo jest znaleźć w przytoczonych zależnościach.
Dalej posłużmy się zapisanymi nierównościami i dodajmy je stronami. Otrzymujemy nierówność: , a po rozwinięciu: , zaś po redukcji wyrazów podobnych i uproszczeniu: , co prowadzi nas do tezy:
c.n.d.
I jeszcze jeden przykład twierdzenia, w dowodzie którego wygodnie jest wykorzystać znane fakty, które jednak nie dla wszystkich są być może oczywiste, a więc warto je najpierw wykazać.
Udowodnimy, że dla każdych dwóch liczb rzeczywistych dodatnich , prawdziwa jest nierówność .
Rozwiązanie
Założenie: i to liczby rzeczywiste.
Teza: .
Dowód:
I znowu na początku dowodu prawdopodobnie wiele osób stwierdzi, że nie wiadomo, jak skorzystać z założenia; nie widzimy żadnej zależności pomiędzy i , którą moglibyśmy zacząć przekształcać, aby dojść do tezy.
Skorzystamy z dwóch zależności.
Pierwsza jest następująca: dla dowolnych liczb rzeczywistych i prawdziwa jest nierówność . Uzasadnienie: .
Druga jest następująca: Jeżeli i są liczbami dodatnimi, to . Uzasadnienie: Sześcian liczby dodatniej jest dodatni, suma liczb dodatnich jest dodatnia, iloczyn liczb dodatnich jest dodatni, iloraz liczb dodatnich jest dodatni.
Przekształcamy lewą stronę naszej tezy:
.
Wyrażenie, które otrzymaliśmy możemy oszacować uwzględniając przyjęte na początku dowodu własności:
.
Stąd mamy: .
c.n.d.
Czasami, aby udowodnić jakąś zależność, wystarczy po prostu przekształcać dane wyrażenie. Posługując się tą metodą uzasadnimy, że jeżeli , , i , to .
Rozwiązanie
Założenie: , , i .
Teza: .
Dowód:
Z zależności wyznaczamy : , podstawiamy do wyrażenia stanowiącego tezę i przekształcamy wyrażenie po lewej stronie znaku równości:
.
Uproszczenia ułamka mogliśmy dokonać, ponieważ z założenia mamy , a więc wyrażenie, przez które upraszczamy ma wartość różną od zera.
c.n.d.
Słownik
wykazanie, że pewne zdanie jest prawdziwe; każdy krok dowodu musi jasno wynikać z poprzednich lub być przyjętym aksjomatem
polega na przyjęciu założeń i bezpośrednim wykazaniu tezy
fakt matematyczny, którego prawdziwość jest ogólnie znana, przyjmowany bez dowodu