Przeczytaj

Funkcja to relacja, która każdemu elementowi z dziedziny przyporządkowuje dokładnie jeden element przeciwdziedziny. Dziedzina i przeciwdziedzina są określone po zdefiniowaniu przyporządkowania. Mówiąc nieformalnie – funkcja to „przepis” na przekształcenie elementu dziedziny. Rozważmy następujący przykład.

Przykład 1

Poniższa tabela opisuje funkcję odwzorowującą zbiór liter w zbiór liczb:

Litera	Liczba
$A$	$0$
$B$	$1$
$C$	$2$
$D$	$3$
$E$	$4$
$F$	$5$
$G$	$6$
$H$	$7$
$I$	$8$
$J$	$9$
$K$	$10$
$L$	$11$
$M$	$12$
$N$	$13$
$O$	$14$
$P$	$15$
$Q$	$16$
$R$	$17$
$S$	$18$
$T$	$19$
$U$	$20$
$W$	$21$
$X$	$22$
$Y$	$23$
$Z$	$24$

Przy pomocy tej tabeli zakodujemy słowo „funkcja”.

Rozwiązanie

Mamy $25$ liter i $25$ liczb. Słowo „ $F$ , $U$ , $N$ , $K$ , $C$ , $J$ , $A$ ” w tym przyporządkowaniu będzie miało zapis: „ $5$ , $20$ , $13$ , $10$ , $2$ , $9$ , $0$ ”.

Oczywiście kodowanie ma sens tylko wtedy, jeśli mamy gwarancję, że wtajemniczona osoba, która otrzyma zaszyfrowaną wiadomość, będzie w stanie ją jednoznacznie odczytać. Powyższy szyfr spełnia ten warunek. Korzystając z podanego układu liczb: „ $5$ , $20$ , $13$ , $10$ , $2$ , $9$ , $0$ ” bez trudu sprawdzimy, że chodzi właśnie o słowo „funkcja”. W tej sytuacji w naturalny sposób stosujemy funkcję odwrotną – działa ona ze zbioru liczb w zbiór liter i po prostu argumentowi z dolnego wiersza przyporządkowuje wartość z górnego.

Mając tę intuicję przypomnijmy pojęcia związane z funkcją odwrotną:

Funkcja „na”

Funkcja jest „na” cały zbiór $Y$ wtedy i tylko wtedy, gdy dla każdego $y \in Y$ istnieje takie $x \in X$ , że $f (x) = y$ .

Funkcja różnowartościowa

Funkcja jest różnowartościowa, jeśli dla dowolnych dwóch argumentów $x_{1}$ , $x_{2} \in X$ z faktu, że $x_{1} \neq x_{2}$ wynika, że $f (x_{1}) \neq f (x_{2})$ .

Bijekcja

Funkcja jest bijekcją, jeśli jest różnowartościowa i „na”.

Funkcja odwrotna

Niech funkcja $f$ : $X \to Y$ będzie bijekcjąbijekcjabijekcją.
Funkcję $f^{- 1}$ : $Y \to X$ nazywamy funkcją odwrotną do funkcji $f$ wtedy i tylko wtedy, gdy $f^{- 1} (y) = x$ dla każdego $x \in X$ i $y \in Y$ .

Wyznaczymy funkcje odwrotne do kilku znanych nam funkcji.

Przykład 2

Wyznaczymy funkcję odwrotną do funkcji $f : (0, \infty) \to (0, \infty)$ , $f (x) = x^{2}$ .

Rozwiązanie

Funkcja $f$ dla wskazanej dziedziny jest różnowartościowafunkcja różnowartościowaróżnowartościowa i „na”, ponieważ przyjmuje jako swoje wartości wszystkie elementy przeciwdziedziny. Zatem istnieje funkcja odwrotna. Wyznaczymy zmienną $x$ z równania: $y = x^{2}$ . Oczywiście $x = \sqrt{y}$ , więc $f^{- 1} (x) = \sqrt{x}$ .

Sprawdźmy:

$(f^{- 1} \circ f) (x) = f^{- 1} (f (x)) = \sqrt{x^{2}} = |x| = x$ , dla $x \in (0, \infty)$ , $f^{- 1} \circ f$ : $(0, \infty) \to (0, \infty)$ .

$(f \circ f^{- 1}) (x) = f (f^{- 1} (x)) = {(\sqrt{x})}^{2} = x$ .

Przykład 3

Wyznaczymy funkcję odwrotną do funkcji $f$ : $ℝ \to (0, \infty)$ .

Rozwiązanie

Aby dane przyporządkowanie było funkcją, która jest różnowartościowa i „na” w swej dziedzinie, musimy rozważać tylko sytuacje, gdy $a > 0$ , ponieważ dla np. $a = - 2$ i $x = \frac{1}{2}$ mielibyśmy $f (\frac{1}{2}) = \sqrt{- 2}$ , a przecież nie istnieje taka liczba rzeczywista, która pomnożona przez samą siebie da nam liczbę ujemną.

Dla $a = 1$ funkcja $f (x) = 1^{x}$ jest funkcją stałą. Dla takiej funkcji nie istnieje funkcja odwrotna, gdyż nie jest ona różnowartościowa.

Jeśli $a > 0$ i $a \neq 1$ , to funkcja jest rosnąca, a więc różnowartościowa i $Z W = (0, \infty)$ , czyli jest „na”.

Istnieje funkcja odwrotnafunkcja odwrotnafunkcja odwrotna do niej i jest to funkcja logarytmiczna:

$f^{- 1}$ : $(0, \infty) \to ℝ$ , gdzie $a > 0$ i $a \neq 1$ .

Sprawdźmy:

$(f^{- 1} \circ f) (x) = f^{- 1} (f (x)) = \log_{a} (a^{x}) = x \cdot 1 = x$ , $f^{- 1} \circ f$ : $ℝ \to ℝ$

$(f \circ f^{- 1}) (x) = f (f^{- 1} (x)) = a^{\log_{a} x} = x$ , $f \circ f^{- 1}$ : $(0, \infty) \to (0, \infty)$

Przykład 4

Sprawdzimy, czy funkcja $f (x) = \frac{x}{x - 1}$ jest odwrotna względem siebie.

Rozwiązanie

Dziedziną funkcji $f$ jest zbiór $D_{f} = ℝ ∖ \{1\}$ .

Jest to funkcja homograficzna, której wykresem jest hiperbola.

Przekształćmy wzór tej funkcji: $f (x) = \frac{x}{x - 1} = \frac{x - 1 + 1}{x - 1} = 1 + \frac{1}{x - 1}$ .

Ze wzoru można odczytać, że wykres tej funkcji powstaje z wykresu funkcji $f_{1} (x) = \frac{1}{x}$ w przesunięciu o wektor $[1, 1]$ .

RQgEtg1EuyBE4

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do sześciu oraz pionową osią Y od minus sześciu do sześciu. Na płaszczyźnie narysowano wykres funkcji f. Wykresem funkcji jest hiperbola o wierzchołkach w punktach 2;2 oraz 0;0. Linią przerywaną zaznaczono asymptotę pionową opisaną wzorem x=1 oraz asymptotę poziomą y=1.

Zbiorem wartości funkcji $f$ jest zbiór $ℝ ∖ \{1\}$ .

Funkcja $f$ : $ℝ ∖ \{1\} \to ℝ ∖ \{1\}$ jest bijekcją, ponieważ jest różnowartościowa i „na”.

Zatem istnieje funkcja odwrotna do niej.

Załóżmy, że jest to ta sama funkcja $f$ .

Sprawdźmy:

$(f \circ f) (x) = f (f (x)) = \frac{\frac{x}{x - 1}}{\frac{x}{x - 1} - 1} = \frac{\frac{x}{x - 1}}{\frac{x - x + 1}{x - 1}} = \frac{x}{1} = x$ .

Zatem funkcja $f$ jest funkcją odwrotną do samej siebie.

Funkcje, które są odwrotne do samej siebie nazywamy inwolucjamiinwolucjainwolucjami.

Wróćmy do kodowania, od którego zaczęliśmy rozważania w tym materiale. Następne przykłady potraktujmy jako zabawę.

Oczywiście kod przedstawiony w Przykładzie 1 jest bardzo prosty. Możemy skomplikować go używając działania zwanego „dodawaniem modulo $25$ ”.

$(a + b) \mod 25 = \{\begin{cases} a + b, & a + b < 25 \\ a + b - 25, & a + b ⩾ 25 \end{cases}$

Wybierzemy dowolną liczbę $p$ ze zbioru $A = \{0, 1, \dots, 24\}$ , niech to będzie

np. $17$ .

Zapiszemy ciąg liczb „ $5$ , $20$ , $13$ , $10$ , $2$ , $9$ , $0$ ” stosując wzajemnie jednoznaczną funkcję liczbową:

$f$ : $A \to A$

$f (5) = (5 + 17) \mod 25 = 22$

$f (20) = (20 + 17) \mod 25 = 12$

$f (13) = (13 + 17) \mod 25 = 5$

$f (2) = (2 + 17) \mod 25 = 19$

$f (9) = (9 + 17) \mod 25 = 1$

$f (0) = (0 + 17) \mod 25 = 17$

Nasza funkcja zakodowała ciąg „ $5$ , $20$ , $13$ , $10$ , $2$ , $9$ , $0$ ” w ciąg „ $22$ , $12$ , $5$ , $19$ , $1$ , $17$ ”. Osoba trzecia, nieznająca funkcji kodującej, miałaby duże problemy z odkodowaniem tego zapisu

Funkcja dekodująca – odwrotna do kodującej – ma w naszym przykładzie postać:

$f^{- 1} (x) = (x - 17) \mod 25 = \{\begin{cases} x - 17, x ⩾ 17 \\ x - 17 + 25, x < 17 \end{cases}$ .

To kodowanie można przedstawić również przy pomocy tabeli:

$x$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$	$11$
$y$	$17$	$18$	$19$	$20$	$21$	$22$	$23$	$24$	$0$	$1$	$2$	$3$

$12$	$13$	$14$	$15$	$16$	$17$	$18$	$19$	$20$	$21$	$22$	$23$	$24$
$4$	$5$	$6$	$7$	$8$	$9$	$10$	$11$	$12$	$13$	$14$	$15$	$16$

Przykład 5

Korzystając z kodowania literkodowanie literkodowania liter i funkcji odkodowującej

$f^{- 1} (x) = (x - 24) \mod 25 = \{\begin{cases} x - 24, x ⩾ 24 \\ x - 24 + 25, x < 24 \end{cases}$

odczytamy napis: „ $3$ , $12$ , $7$ , $5$ , $11$ , $24$ ”.

Rozwiązanie

$f^{- 1} (3) = (3 - 24 + 25) \mod 25 = 4$

$f^{- 1} (12) = (12 - 24 + 25) \mod 25 = 13$

$f^{- 1} (7) = (7 - 24 + 25) \mod 25 = 8$

$f^{- 1} (5) = (5 - 24 + 25) \mod 25 = 6$

$f^{- 1} (11) = (11 - 24 + 25) \mod 25 = 12$

$f^{- 1} (24) = (24 - 24) \mod 25 = 0$

Posługując się tabelkątabelkatabelką odkodowujemy napis: „ $E$ , $N$ , $I$ , $G$ , $M$ , $A$ ”.

Przykład 6

Niech $p = 19 \in A = \{0, 1, \dots, 24\}$ . Posługując się kodowaniem literkodowanie literkodowaniem liter zaszyfrujemy słowo „ $K R Y P T O G R A F I A$ ”.

Rozwiązanie

Zapis „ $K R Y P T O G R A F I A$ ” po zastosowaniu przyporządkowania z tabelkitabelkatabelki to:
„ $10$ , $17$ , $23$ , $15$ , $19$ , $14$ , $17$ , $0$ , $5$ , $8$ , $0$ ”. Stosując funkcję kodującą dla $p = 19$ otrzymujemy:

$f (10) = (10 + 19) \mod 25 = 4$

$f (17) = (17 + 19) \mod 25 = 11$

$f (23) = (23 + 19) \mod 25 = 17$

$f (15) = (15 + 19) \mod 25 = 9$

$f (19) = (19 + 19) \mod 25 = 13$

$f (14) = (14 + 19) \mod 25 = 8$

$f (17) = (17 + 19) \mod 25 = 11$

$f (0) = (0 + 19) \mod 25 = 19$

$f (5) = (5 + 19) \mod 25 = 24$

$f (8) = (8 + 19) \mod 25 = 2$

$f (0) = (0 + 19) \mod 25 = 19$

Zapis: „ $10$ , $17$ , $23$ , $15$ , $19$ , $14$ , $17$ , $0$ , $5$ , $8$ , $0$ ” uzyskany po zakodowaniu to:
„ $4$ , $11$ , $17$ , $9$ , $13$ , $8$ , $11$ , $19$ , $24$ , $2$ , $19$ ”.

Problem 1

Wybierz liczbę $p$ należącą do zbioru $A = \{0, 1, \dots, 24\}$ . Zakoduj dowolne słowo i poproś kolegę o rozkodowanie Twojego hasła nie znając liczby $p$ .

Ciekawostka

Dana jest funkcja $f$ : $ℝ \to ℝ$ . Jest to funkcja liniowa, różnowartościowa i „na”funkcja „na”„na”. Łatwo znaleźć funkcję odwrotną: $f^{- 1} (x) = \frac{1}{2} x$ . Rozważmy funkcję określoną tym samym wzorem, ale na okrojonej do liczb naturalnych $ℕ_{+}$ (bez zera) dziedzinie. Wówczas zbiorem wartości funkcji $g (n) = 2 n$ jest zbiór $g (ℕ) = P$ , gdzie $P$ oznacza zbiór liczb parzystych dodatnich.

R1FxlzKLfoKzx

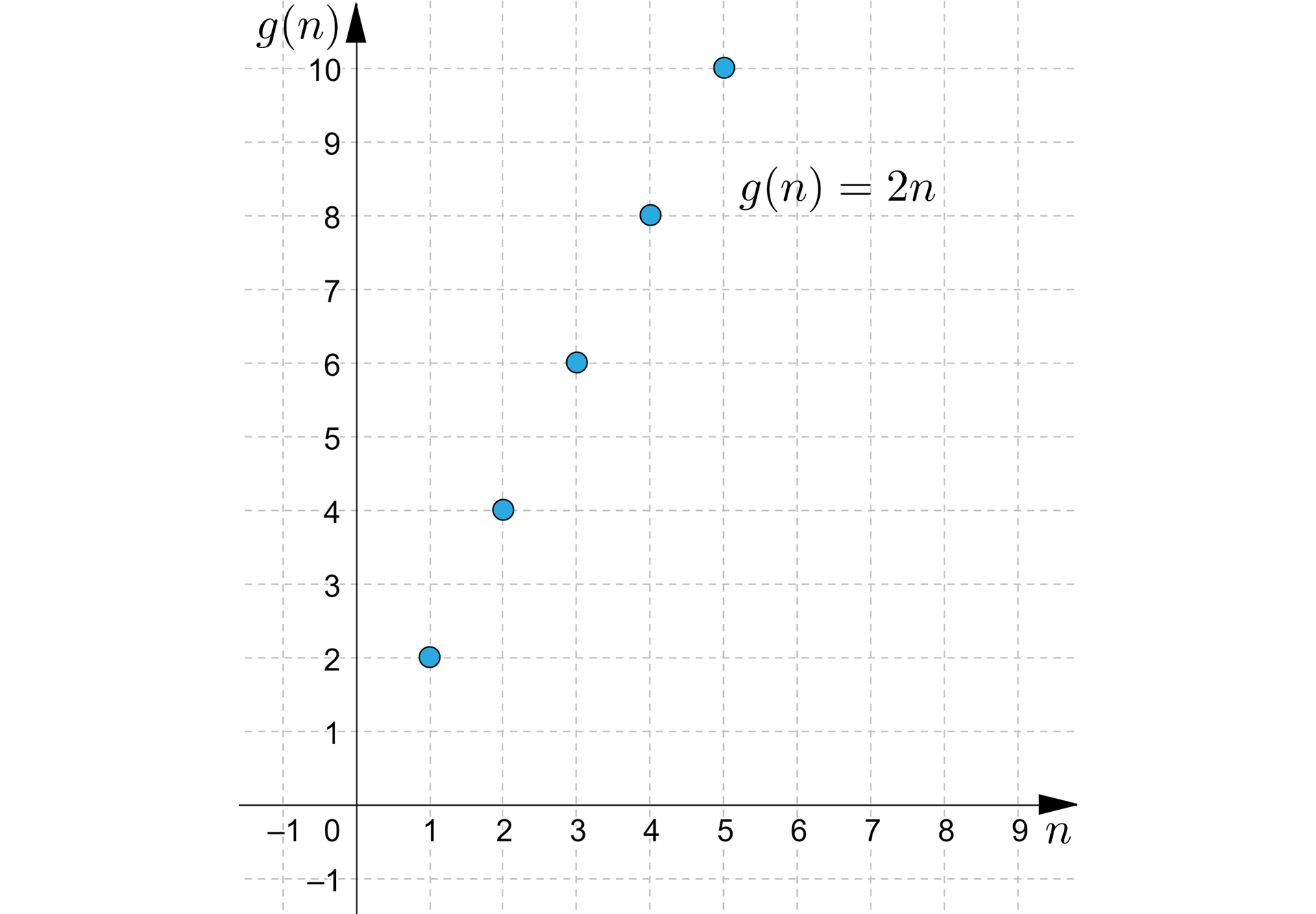
Na ilustracji przedstawiono układ współrzędnych z poziomą osią od minus jeden do dziewięciu reprezentującą zbiór liczb n oraz z pionową osią od minus jeden do dziesięciu reprezentującą wartości funkcji gn. Na płaszczyźnie kropkami zaznaczono punkty o następujących współrzędnych 1;2, 2;4, 3;6, 4;8 oraz 5;10. Obok zapisano równanie gn=2n.

Pojęciem, które nas wszystkich bardzo intryguje jest nieskończoność. Filozofowie rozróżniają nieskończoność potencjalną i nieskończoność aktualną. Zbiór liczb naturalnych jest przykładem tej drugiej. Bardzo ciekawe jest określenie równoliczności. Mówimy, że dwa zbiory są równoliczne, gdy istnieje funkcja wzajemnie jednoznaczna przekształcająca jeden zbiór na drugi. Studenci pierwszego roku matematyki są zazwyczaj bardzo zaskoczeni, gdy dowiadują się, że zbiór liczb naturalnych jest równoliczny ze zbiorem liczb parzystych. Taką funkcją jest właśnie funkcja $g$ . Kiedy dwa zbiory są skończone, użycie sformułowania „tyle samo elementów” jest dla nas bardzo jasne. Jednak w przypadku zbiorów nieskończonych nie jest to już tak intuicyjne i właściwe. Wydaje się przecież, że liczb naturalnych jest dwa razy więcej niż liczb parzystych.

Funkcja $g$ : $ℕ \to P$ jest rosnąca, a więc różnowartościowa. Jest „na”. Istnieje zatem funkcja do niej odwrotna $g^{- 1}$ : $P \to ℕ$ , $g^{- 1} (x) = \frac{1}{2} x$ .

Słownik

funkcja „na”

funkcja jest „na” cały zbiór $Y$ wtedy i tylko wtedy, gdy dla każdego $y \in Y$ istnieje takie $x \in X$ , że $f (x) = y$

funkcja różnowartościowa

funkcja jest różnowartościowa jeśli dla dowolnych dwóch argumentów $x_{1}$ , $x_{2} \in X$ z faktu, że $x_{1} \neq x_{2}$ wynika, że $f (x_{1}) \neq f (x_{2})$

bijekcja

funkcja jest bijekcją jeśli jest różnowartościowa i „na”

funkcja odwrotna

niech funkcja $f$ : $X \to Y$ będzie bijekcją; funkcję $f^{- 1}$ : $Y \to X$ nazywamy funkcją odwrotną do funkcji $f$ jeśli wtedy i tylko wtedy, gdy $f^{- 1} (y) = x$ dla każdego $x \in X$ i $y \in Y$

inwolucja

funkcja, która ma funkcję odwrotną równą jej samej

kodowanie liter

$12$	$13$	$14$	$15$	$16$	$17$	$18$	$19$	$20$	$21$	$22$	$23$	$24$
$4$	$5$	$6$	$7$	$8$	$9$	$10$	$11$	$12$	$13$	$14$	$15$	$16$

tabelka

Wprowadzenie

Schemat interaktywny

Słownik