Przeczytaj

Podajmy definicję, kiedy dwie proste są prostopadłe w przestrzeni.

proste prostopadłe w przestrzeni

Definicja: proste prostopadłe w przestrzeni

Mówimy, że dwie proste $l$ i $k$ w przestrzeni są prostopadłe, jeżeli istnieje prosta $l_{1}$ równoległa do prostej $l$ i przecinająca prostą $k$ pod kątem prostym.

R1DCessDWYePj

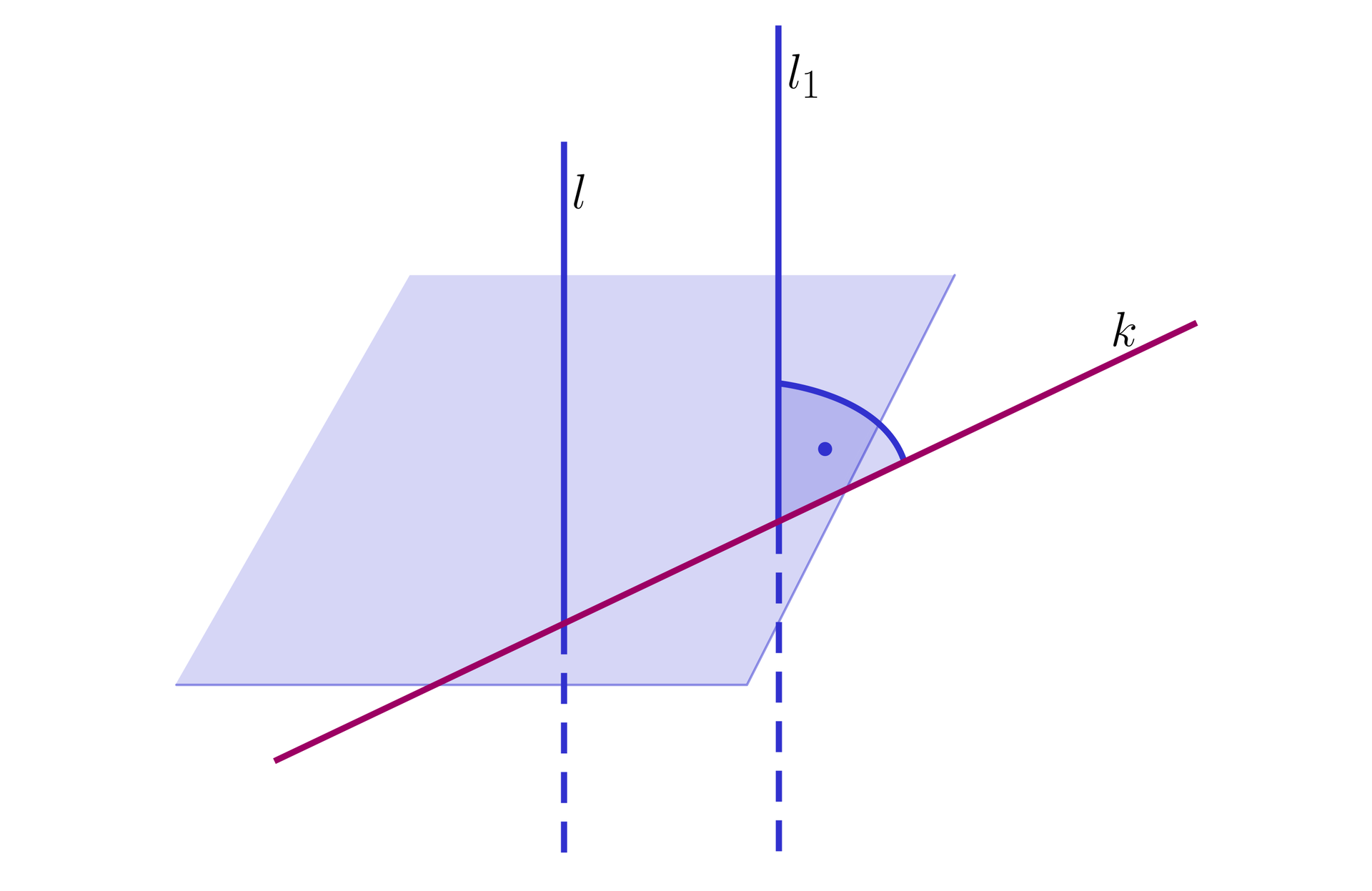
Ilustracja przedstawia dwie równoległe proste, prostą l oraz prostą l indeks dolny jeden koniec indeksu. Obie te proste są prostopadłe do prostej k oraz płaszczyzny zawartej w tej prostej.

Ważne!

Proste, które są prostopadłe w przestrzeni przecinają się lub są skośne (nie leżą w jednej płaszczyźnie – nie mają punktów wspólnych).

Proste, które są prostopadłe w przestrzeni mogą być położone:

w tej samej płaszczyźnie i przecinają się pod kątem $90 °$
REfBhNJhiu9Av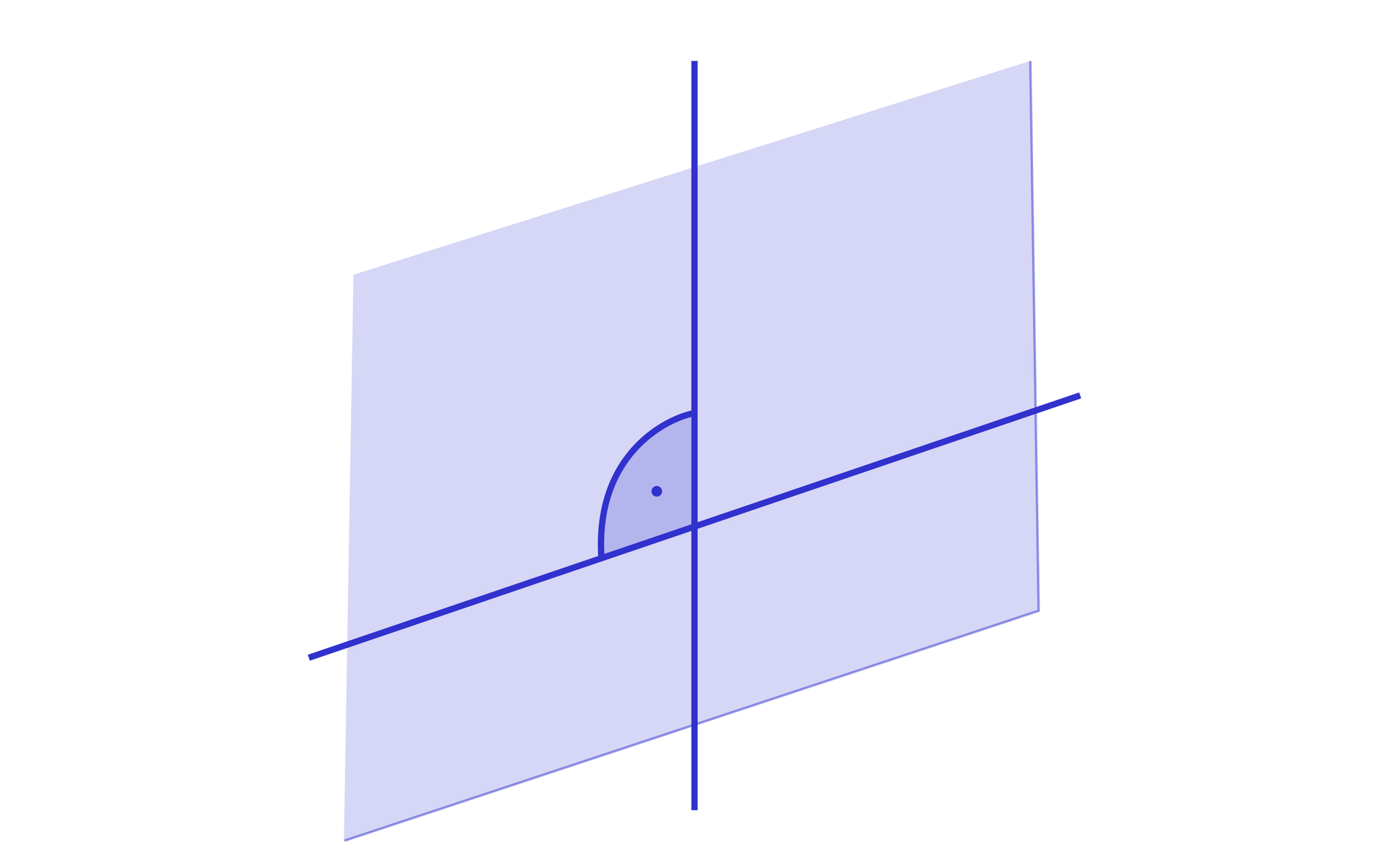
w dwóch różnych płaszczyznach – są skośne i przecinają się pod kątem $90 °$
RyBAqcI5oGqXM

Przykład 1

Na rysunku przedstawiono proste $k$ i $l$ , które są zawarte w tej samej płaszczyźniepłaszczyznapłaszczyźnie. Sprawdzimy, czy proste są prostopadłe, jeżeli wiadomo, że $α = \frac{4}{5} β$ .

RW829SwvIkYeY

Ilustracja przedstawia dwie proste zawarte w tej samej płaszczyźnie, prosta l oraz prosta k. Obie proste przecinają się tworząc dwa kąty przyległe, kąt alfa oraz kąt beta.

Rozwiązanie:

Zauważmy, że $α + β = 180 °$ .

Z warunków w zadaniu wynika, że $α = \frac{4}{5} β$ .

Zatem:

$\frac{4}{5} β + β = 180 °$

$\frac{9}{5} β = 180 °$

$β = 100 °$

Wobec tego $α = 80 °$ .

Ponieważ proste przecinają się pod kątem różnym od $90 °$ , zatem nie są prostopadłe.

Przykład 2

Na rysunku przedstawiono sześcian $A B C D E F G H$ . Wskażemy proste, zawierające pozostałe krawędzie sześcianu, które są prostopadłe do prostej zawierającej krawędź $A E$ .

RcfemWy9WWwly

Ilustracja przedstawia sześcian A B C D E F G H, gdzie wierzchołek E znajduje się nad A, wierzchołek F nad B, wierzchołek G nad C, wierzchołek H nad D. Przez odcinek A E poprowadzono czerwoną prostą.

Rozwiązanie:

Proste, zawierające pozostałe krawędzie sześcianu, które są prostopadłe do prostej zawierającej krawędź $A E$ sześcianu, to:

$A D$ , $A B$ , $B C$ , $C D$ , $E H$ , $E F$ , $F G$ , $G H$ .

Przykład 3

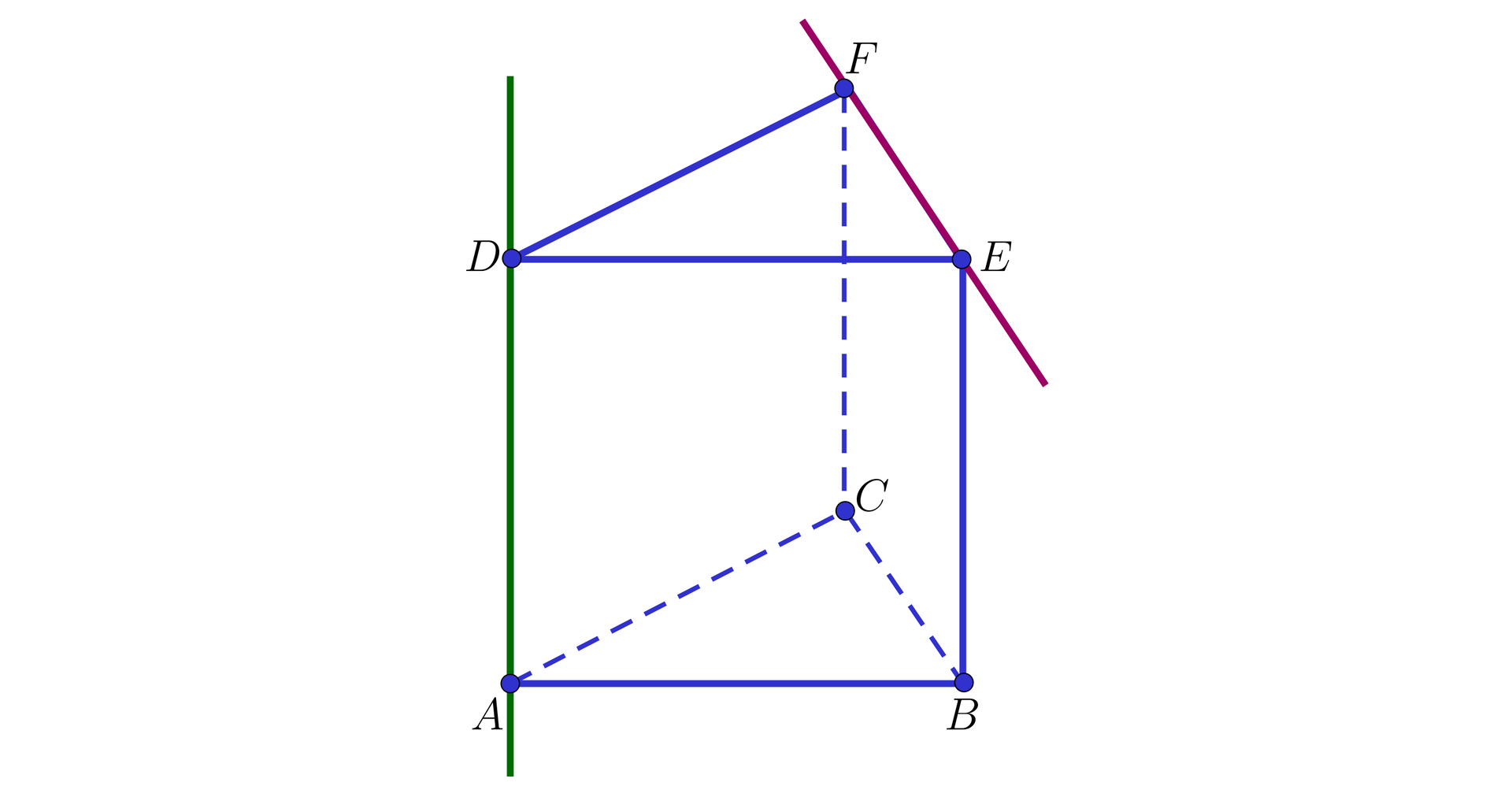
Wykażemy, że proste zawierające odcinki $A B$ i $C D$ są prostopadłe, jeżeli wiadomo, że punkt $D$ jest środkiem odcinka $A B$ w sześcianie, jak na poniższym rysunku.

RoKrVLheM3jKP

Ilustracja przedstawia sześcian o krawędzi a. Zostały zaznaczone dwie przekątne przyległych ścian bocznych poprowadzone z jednego punktu C znajdującego się w górnej podstawie, przekątna A C oraz B C. Poprowadzono również przekątną podstawy dolnej A B. Powstał trójkąt równoboczny A B C. Z wierzchołka C na podstawę A B w punkcie D upuszczono wysokość trójkąta.

Rozwiązanie:

Zauważmy, że odcinki $A C$ i $B C$ są równej długości, ponieważ są przekątnymi ścian sześcianu.

Zatem trójkąt $A B C$ jest równoramienny.

Ponieważ punkt $D$ jest środkiem odcinka $A B$ , zatem odcinek $C D$ jest wysokością trójkąta $A B C$ .

Wobec tego odcinki $A B$ i $C D$ są prostopadłe, co oznacza że proste zawierające te odcinki są także prostopadłe.

Przykład 4

Określimy, których prostych zawierających krawędzie graniastosłupa prawidłowego trójkątnegograniastosłup prawidłowy trójkątnygraniastosłupa prawidłowego trójkątnego z rysunku jest więcej: prostopadłych do prostej zawierającej krawędź $A D$ , czy krawędź $E F$ .

R1PCUuH3RISyh

Ilustracja przedstawia graniastosłup prawidłowy trójkątny A B C D E F, gdzie wierzchołek D znajduje się nad A, wierzchołek E nad B, wierzchołek F nad C. Zaznaczono także dwie proste, pierwsza zawarta została w odcinku A D, druga natomiast przechodzi przez krawędź E F.

Rozwiązanie:

Proste prostopadłe do prostej zawierającej krawędź $A D$ to: $A B$ , $A C$ , $B C$ , $D E$ , $E F$ , $D F$ .

Proste prostopadłe do prostej zawierającej krawędź $E F$ to: $C F$ , $B E$ , $A D$ .

Zatem prostych prostopadłych do prostej zawierającej krawędź $A D$ jest o $3$ więcej niż prostych prostopadłych do prostej zawierającej krawędź $E F$ .

Ciekawostka

Jeżeli prosta przedstawia się za pomocą równania parametrycznego, to wówczas możemy badać prostopadłość prostych w przestrzeni za pomocą odpowiednich zależności.

Równanie parametryczne prostej:

Niech $P = (x_{0}, y_{0}, z_{0})$ będzie punktem należącym do prostej $l$ , która jest równoległa do wektora $\vec{u} = [u_{1}, u_{2}, u_{3}]$ .

Wówczas równanie parametryczne prostej $l$ ma postać:

\{\begin{cases} x = x_{o} + t \cdot u_{1} \\ y = y_{o} + t \cdot u_{2} \\ z = z_{o} + t \cdot u_{3} \end{cases}

, gdzie

t \in ℝ

oraz

{u_{1}}^{2} + {u_{2}}^{2} + {u_{3}}^{2} > 0

o prostopadłości prostych w przestrzeni

Twierdzenie: o prostopadłości prostych w przestrzeni

Proste $l_{1}$ i $l_{2}$ o wektorach kierunkowych (równoległych do tych prostych) odpowiednio $\vec{u} = [u_{1}, u_{2}, u_{3}]$ i $\vec{v} = [v_{1}, v_{2}, v_{3}]$ są prostopadłe w przestrzeni wtedy, gdy iloczyn skalarnyiloczyn skalarnyiloczyn skalarny ich wektorów kierunkowych jest równy $0$ , czyli:

\vec{u} \circ \vec{v} = 0

Wobec tego proste o wektorach kierunkowych $\vec{u} = [u_{1}, u_{2}, u_{3}]$ i $\vec{v} = [v_{1}, v_{2}, v_{3}]$ są prostopadłe w przestrzeni wtedy, gdy zachodzi warunek:

u_{1} \cdot v_{1} + u_{2} \cdot v_{2} + u_{3} \cdot v_{3} = 0

Przykład 5

Wyznaczymy, dla jakich wartości parametru $m$ proste $l_{1}$ i $l_{2}$ o wektorach kierunkowych $\vec{u} = [m, - m, 6]$ i $\vec{v} = [m, - 1, - 2]$ są prostopadłe.

Rozwiązanie:

Proste są prostopadłe, gdy iloczyn skalarny ich wektorów kierunkowych jest równy $0$ .

Wobec tego:

$\vec{u} \circ \vec{v} = [m, - m, 6] \circ [m, - 1, - 2] = m^{2} + m - 12$

Zatem do wyznaczenia wartości parametru $m$ rozwiązujemy równanie:

$m^{2} + m - 12 = 0$

$Δ = 1 - 4 \cdot (- 12) = 49$

$m_{1} = \frac{- 1 - 7}{2} = - 4$

$m_{2} = \frac{- 1 + 7}{2} = 3$

Czyli $m \in \{- 4, 3\}$ .

Słownik

płaszczyzna

pojęcie pierwotne w geometrii Euklidesa

iloczyn skalarny

dwuargumentowa funkcja, przyporządkowująca dwóm danym wektorom przestrzeni liniowej pewną wartość liczbową

graniastosłup prawidłowy trójkątny

graniastosłup prosty, którego podstawą jest trójkąt równoboczny

Wprowadzenie

Schemat interaktywny

Słownik