Przeczytaj

Przegląd przykładowych zadań rozpoczniemy od interpretacji geometrycznej wartości bezwzględnej.

Przykład 1

Znajdziemy wszystkie liczby $x$ , które spełniają nierówność $|x| < 5$ .

Rozwiązanie:

$I$ sposób:

Mamy znaleźć wszystkie liczby $x$ , które – zgodnie z definicją wartości bezwzględnejwartości bezwzględnej – są odległe od zera o mniej niż $5$ jednostek.
Ponieważ $|x| = 5$ wtedy i tylko wtedy, gdy $x = - 5$ lub $x = 5$ , więc po zaznaczeniu na osi liczbowej tych dwóch liczb znajdujemy przedział, w którym są wszystkie liczby spełniające daną nierówność.

RSGJmrINBRptO

Ilustracja przedstawia poziomą oś X, na której zaznaczono liczby: minus 5, 0 oraz 5 i narysowano przedział otwarty od minus pięciu do pięciu. Punkty minus 5 i 5 zaznaczono niezamalowanymi kółkami.

A zatem zbiór wszystkich szukanych liczb $x$ tworzy przedział otwarty $(- 5, 5)$ .

$II$ sposób:

Rozpatrzmy dwa rozłączne przypadki:

$x < 0$ ; wtedy $|x| = - x$ , zatem dana nierówność jest równoważna nierówności
$- x < 5$ , skąd $x > - 5$ .
Oznacza to, że daną nierówność spełniają wszystkie liczby $x \in (- 5, 0)$ .
$x \geq 0$ ;
wtedy $|x| = x$ , więc dana nierówność jest równoważna nierówności
$x < 5$ .
Oznacza to, że daną nierówność spełniają wszystkie liczby $x \in ⟨0, 5)$ .

Wynika stąd, że $x \in (- 5, 0) \cup ⟨0, 5)$ , czyli $x \in (- 5, 5)$ .

Odpowiedź: $x \in (- 5, 5)$ .

Przykład 2

Znajdziemy wszystkie liczby $x$ , które spełniają nierówność $|x + 3| \geq 4$ .

Rozwiązanie:

$I$ sposób:

Zapisujemy daną nierówność w postaci $\left|x-\left(-3\right)\right|\geq4$ .
Szukamy zatem wszystkich liczb $x$ , które są odległe od liczby $- 3$ o co najmniej $4$ jednostki.
Zaznaczmy na osi liczbowej odcinek o środku w punkcie $- 3$ i długości $8$ .
Ma on końce w punktach $- 7$ oraz $1$ .

R1N93BEJWVOSJ

Ilustracja przedstawia poziomą oś X od minus siedmiu do jeden. Na osi zaznaczono trzy przedziały domknięte i opisano ich długości. Przedział pierwszy od minus siedmiu do minus trzech ma długość cztery, przedział drugi od minus trzech do jeden ma długość 4, przedział od minus siedmiu do jeden ma długość osiem.

Te końce, to takie dwie liczby na osi liczbowej, które są odległe od $- 3$ o $4$ jednostki, czyli są to rozwiązania równania $|x + 3| = 4$ .

Pozostaje nam zaznaczyć na osi liczbowej dwa rozłączne przedziały, w których są liczby spełniające daną nierówność.

RYLnH3xFaMv8T

Ilustracja przedstawia poziomą oś X od minus siedmiu do jeden. Na osi zaznaczono dwa rozłączne przedziały. Pierwszy przedział jest prawostronnie domknięty od minus nieskończoności do minus siedmiu, drugi przedział jest lewostronnie domknięty od jeden do plus nieskończoności.

A zatem zbiór wszystkich szukanych liczb $x$ to suma dwóch przedziałów: $(- \infty, - 7⟩$ oraz $⟨1, \infty)$ .

$II$ sposób:

Rozpatrzmy dwa rozłączne przypadki:

$x < - 3$ ; wtedy $|x + 3| = - 3 - x$ , więc dana nierówność jest równoważna nierówności
$-x-3\geq4$ , skąd $-x\geq7$ , czyli $x\leq-7$ .
Oznacza to, że daną nierówność spełniają wszystkie liczby $x \in (- \infty, - 7⟩$ .
$x\geq-3$ ;
wtedy $|x + 3| = x + 3$ , więc dana nierówność jest równoważna nierówności
$x+3\geq4$ , skąd $x\geq1$ .
Oznacza to, że daną nierówność spełniają wszystkie liczby $x \in ⟨1, \infty)$ .

Wynika stąd, że $x \in (- \infty, - 7⟩$ lub $x \in ⟨1, \infty)$ .

Odpowiedź: $x \in (- \infty, - 7⟩ \cup ⟨1, \infty)$ .

Ważne!

Zauważmy, że dla danej liczby rzeczywistej $a$ i dodatniej liczby $r\geq0$ rozwiązaniem równania $|x - a| = r$ są liczby $a - r$ oraz $a + r$ , leżące na osi liczbowej w odległości $r$ od liczby $a$ .

R17L6OZ9pgpMu

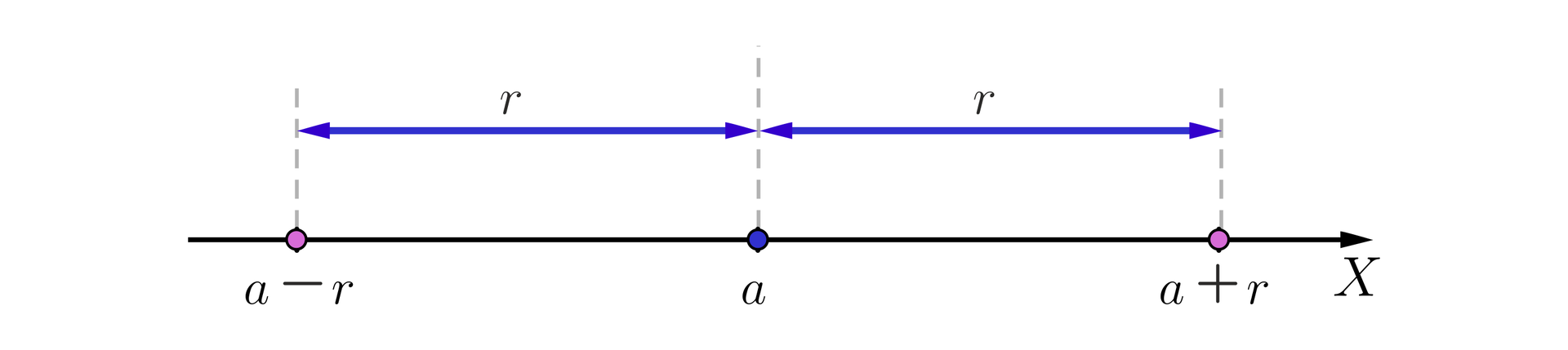
Ilustracja przedstawia poziomą oś X. Na środku osi zaznaczono punkt a. Po jego lewej stronie zaznaczono punkt a odjąć r i podpisano, iż odległość między tymi punktami wynosi r. Na prawo od punktu a zaznaczono punkt a dodać r i również podpisano, że odległość wynosi r.

Zatem dla dowolnych liczb rzeczywistych $a$ oraz $r\geq0$ mamy:

$\left|x-a\right|\leq r$ wtedy i tylko wtedy, gdy $x\geq a-r$ i $x\leq a+r$ , czyli gdy $x \in ⟨a - r, a + r⟩$ ,
$\left|x-a\right|\geq r$ wtedy i tylko wtedy, gdy $x\leq a-r$ lub $x\geq a+r$ , czyli gdy $x \in (- \infty, a - r⟩ \cup ⟨a + r, \infty)$ .

Przykład 3

Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych $x$ , które spełniają nierówność $|x - n| \leq k$ .

RBAmPR1GqYkD1

Ilustracja przedstawia poziomą oś X od minus dwóch do pięciu. Na osi zaznaczono przedział domknięty od minus dwóch do pięciu.

Obliczymy wartości $n$ oraz $k$ .

Rozwiązanie:

$I$ sposób:

Zauważmy, że:

$n$ jest środkiem przedziału $⟨- 2, 5⟩$ , co oznacza, że $n = \frac{- 2 + 5}{2} = \frac{3}{2}$ ,
odległość między krańcami przedziału $⟨- 2, 5⟩$ (czyli długość tego przedziału) jest równa $2 k$ , skąd wynika, że $k = \frac{|5 - (- 2)|}{2} = \frac{7}{2}$ .

Wobec tego $n = \frac{3}{2} = 1 \frac{1}{2}$ oraz $k = \frac{7}{2} = 3 \frac{1}{2}$ .

R3obpQDvQzpNU

Ilustracja przedstawia poziomą oś X od minus dwóch do pięciu. Na osi zaznaczono przedział domknięty od minus dwóch do pięciu. Zaznaczono środek przedziału o współrzędnej jeden i jedna druga i podpisano, że odległość między punktem jeden i jedna druga a lewym końcem przedziału wynosi 3 i jedna druga i również tyle wynosi odległość między środkiem przedziału a prawym jego krańcem.

$II$ sposób:

Skorzystamy z wniosku zapisanego pod poprzednim przykładem.

Ponieważ wszystkie liczby $x$ , które spełniają nierówność $\left|x-n\right|\leq k$ to liczby, które należą do przedziału $⟨n - k, n + k⟩$ , więc $n - k = - 2$ oraz $n + k = 5$ .
Stąd $2 k = 2 + 5 = 7$ oraz $2 n = 5 - 2 = 3$ , czyli $n = \frac{3}{2} = 1 \frac{1}{2}$ oraz $k = \frac{7}{2} = 3 \frac{1}{2}$ .

Wykazaliśmy zatem, że liczby z przedziału $⟨- 2, 5⟩$ są rozwiązaniem nierówności $\left|x-1\frac12\right|\leq3\frac12$ .

Przykład 4

Rozwiążemy nierówności:

$||x - 5| - 4| \leq 3$ ,
$||x + 2| - 4| \geq 6$ .

Rozwiązanie

$||x - 5| - 4| \leq 3$
Przekształcamy daną nierówność równoważnie, korzystając z omówionych powyżej własności nierówności z wartością bezwzględnąwartością bezwzględną: $||x - 5| - 4| \leq 3$ wtedy i tylko wtedy, gdy $|x - 5| \in ⟨4 - 3, 4 + 3⟩$ , czyli $|x - 5| \in ⟨1, 7⟩$ , co oznacza, że $|x - 5| \geq 1$ i $|x - 5| \leq 7$ . Rozwiązujemy otrzymane w ten sposób nierówności:
$|x - 5| \geq 1$ wtedy i tylko wtedy, gdy $x \in (- \infty, 5 - 1⟩ \cup ⟨5 + 1, \infty)$ , czyli dla $x \in (- \infty, 4⟩ \cup ⟨6, \infty)$ ,
$|x - 5| \leq 7$ wtedy i tylko wtedy, gdy $x \in ⟨5 - 7, 5 + 7⟩$ , czyli dla $x \in ⟨- 2, 12⟩$ .
Na koniec sprawdzamy, że układ (koniunkcja) dwóch otrzymanych warunków:
$x \in (- \infty, 4⟩ \cup ⟨6, \infty)$ oraz $x \in ⟨- 2, 12⟩$ jest spełniony dla $x \in ⟨- 2, 4⟩ \cup ⟨6, 12⟩$ .
Otrzymujemy więc, że rozwiązaniami danej nierówności są liczby $x \in ⟨- 2, 4⟩ \cup ⟨6, 12⟩$ .
$||x + 2| - 4| \geq 6$
Przekształcamy daną nierówność równoważnie, korzystając z omówionych powyżej własności nierówności z wartością bezwzględnąwartością bezwzględną:
$||x + 2| - 4| \geq 6$ wtedy i tylko wtedy, gdy $|x + 2| \leq 4 - 6 = - 2$ lub $|x + 2| \geq 4 + 6 = 10$ .
Pierwsza z otrzymanych nierówności jest sprzeczna (a to dlatego, że dla dowolnej liczby rzeczywistej $x$ prawdziwa jest nierówność $|x + 2| \geq 0$ ), więc pozostaje rozwiązać drugą nierówność:
$|x + 2| \geq 10$ wtedy i tylko wtedy, gdy $x \leq - 2 - 10 = - 12$ lub $x \geq - 2 + 10 = 8$ .
Oznacza to, że rozwiązaniami danej nierówności są liczby
$x \in (- \infty, - 12⟩ \cup ⟨8, \infty)$ .

Przykład 5

Znajdziemy wszystkie liczby $x$ , które spełniają nierówność:

$\sqrt{x^{2} - 6 x + 9} + \sqrt{x^{2} + 16 x + 64} < 10$ ,
$|x - 5| + |x + 10| < |3 x + 30|$ .

Rozwiązanie

$\sqrt{x^{2} - 6 x + 9} + \sqrt{x^{2} + 16 x + 64} < 10$
Ponieważ dla każdej liczby rzeczywistej $x$ prawdziwe są zależności:
$\sqrt{x^{2} - 6 x + 9} = \sqrt{{(x - 3)}^{2}} = |x - 3|$
oraz $\sqrt{x^{2} + 16 x + 64} = \sqrt{{(x + 8)}^{2}} = |x + 8|$ ,
więc dana nierówność jest równoważna nierówności
$|x - 3| + |x + 8| < 10$ .
Zauważmy, że liczba $x$ spełnia nierówność $|x - 3| + |x + 8| < 10$
wtedy i tylko wtedy, gdy na osi liczbowejoś liczbowaosi liczbowej suma odległości $x$ od liczb $3$ oraz $- 8$ jest mniejsza od $10$ .
Jednakże odległość między $3$ i $- 8$ jest równa $11$ , a więc suma $|x - 3| + |x + 8|$ jest większa lub równa $11$ .
To spostrzeżenie możemy potwierdzić, korzystając z nierówności trójkątanierówność trójkątanierówności trójkąta. Na tej podstawie stwierdzamy, że

$|x - 3| + |x + 8| = |3 - x| + |x + 8| \geq |3 - x + x + 8| = |11| = 11$
dla dowolnej liczby rzeczywistej $x$ .
Oznacza to, że dana nierówność nie ma rozwiązań.
$|x - 5| + |x + 10| < |3 x + 30|$
Ponieważ dla dowolnej liczby rzeczywistej $x$ prawdziwa jest zależność $|3 x + 30| = 3 \cdot |x + 10|$ , więc daną nierówność możemy przekształcić równoważnie do postaci
$|x - 5| + |x + 10| < 3 |x + 10|$ ,
czyli $|x - 5| < 2 |x + 10|$ .
Rozpatrzmy na osi liczbowejoś liczbowaosi liczbowej trzy przedziały:
$(- \infty, - 10)$ , $⟨- 10, 5)$ oraz $⟨5, + \infty)$ .
Otrzymujemy następujące przypadki:
1. $x \in (- \infty, - 10)$ ;
  wtedy $2 |x + 10| = 2 (- x - 10) = - 2 x - 20$ oraz $|x - 5| = - x + 5$ ,
2. $x \in ⟨- 10, 5)$ ;
  wtedy $2 |x + 10| = 2 (x + 10) = 2 x + 20$ oraz $|x - 5| = - x + 5$ ,
3. $x \in ⟨5, + \infty)$ ;
  wtedy $2 |x + 10| = 2 (x + 10) = 2 x + 20$ oraz $|x - 5| = x - 5$ .
Wówczas:
- w przypadku pierwszym otrzymujemy nierówność
  $- x + 5 < - 2 x - 20$ , skąd $x < - 25$ .
  Bierzemy część wspólną założonego przedziału: $x \in (- \infty, - 10)$ oraz otrzymanego zbioru rozwiązań: $x \in (- \infty, - 25)$ i otrzymujemy, że w tym przypadku rozwiązaniami nierówności są $x \in (- \infty, - 25)$ .
- w przypadku drugim otrzymujemy nierówność
  $- x + 5 < 2 x + 20$ , skąd $- 15 < 3 x$ , czyli $x > - 5$ .
  Bierzemy część wspólną założonego przedziału: $x \in ⟨- 10, 5)$ oraz otrzymanego zbioru rozwiązań: $x \in (- 5, + \infty)$ i otrzymujemy, że w tym przypadku rozwiązaniami nierówności są $x \in (- 5, 5)$ .
- w przypadku trzecim otrzymujemy nierówność
  $x - 5 < 2 x + 20$ ,
  skąd $- 5 - 20 < 2 x - x$ ,
  czyli $x > - 25$ .
  
  Bierzemy część wspólną założonego przedziału: $x \in ⟨5, + \infty)$ oraz otrzymanego zbioru rozwiązań: $x \in (- 25, + \infty)$ i otrzymujemy, że w tym przypadku rozwiązaniami nierówności są $x \in ⟨5, + \infty)$ .
Sumując przedziały otrzymane w każdym z rozpatrywanych przypadków, rozwiązaniami danej nierówności są $x \in (- \infty, - 25) \cup (- 5, 5) \cup ⟨5, + \infty)$ , czyli $x \in (- \infty, - 25) \cup (- 5, + \infty)$ .
Przy okazji zauważmy, że:
- bezpośrednim rachunkiem można sprawdzić, że odległość na osi liczbowejoś liczbowaosi liczbowej każdej z liczb $- 25$ oraz $- 5$ od $5$ jest $2$ razy większa niż odległość od $- 10$ ,
- liczba $x$ spełnia nierówność $|x - 5| < 2 |x + 10|$ wtedy i tylko wtedy, gdy na osi liczbowejoś liczbowaosi liczbowej odległość $x$ od $5$ jest mniejsza od podwojonej odległości $x$ od $- 10$ .
- analizując położenie $x$ na osi liczbowejoś liczbowaosi liczbowej względem liczb $- 25$ oraz $- 5$ , można następnie wywnioskować, że powyższy warunek jest spełniony wtedy i tylko wtedy, gdy $x \in (- \infty, - 25) \cup (- 5, + \infty)$ .

Przykład 6

Rozwiążemy nierówność

$|x + 4| + |3 x - 6| \leq 8$ ,
$|x + 1| - |x - 5| \geq x - 3$ .

Rozwiązanie

$|x + 4| + |3 x - 6| \leq 8$
Korzystając z definicji wartości bezwzględnejwartości bezwzględnej, otrzymujemy:
$|x + 4| = \{\begin{cases} x + 4, dla x \geq - 4 \\ - x - 4, dla x < - 4 \end{cases}$
oraz
$|3 x - 6| = 3 |x - 2| = \{\begin{cases} 3 (x - 2), dla x \geq 2 \\ - 3 (x - 2), dla x < 2 \end{cases}$
Rozpatrujemy zatem na osi liczbowejoś liczbowaosi liczbowej trzy przedziały:
$(- \infty, - 4)$ , $⟨- 4, 2)$ oraz $⟨2, + \infty)$ .
Otrzymujemy więc trzy następujące przypadki:
1. $x \in (- \infty, - 4)$ ; wtedy $|x + 4| = - x - 4$ oraz $|3 x - 6| = 3 |x - 2| = - 3 (x - 2) = - 3 x + 6$ ,
2. $x \in ⟨- 4, 2)$ ; wtedy $|x + 4| = x + 4$ oraz $|3 x - 6| = 3 |x - 2| = - 3 (x - 2) = - 3 x + 6$ ,
3. $x \in ⟨2, + \infty)$ ; wtedy $|x + 4| = x + 4$ oraz $|3 x - 6| = 3 |x - 2| = 3 (x - 2) = 3 x - 6$ .
Wobec tego:
$x + 4 + 3 x - 6 \leq 8$ ,
skąd $x + 3 x \leq 8 - 4 + 6$ , $4 x \leq 10$ ,
czyli $x \leq \frac{5}{2} = 2 \frac{1}{2}$ .
Bierzemy część wspólną założonego przedziału: $x \in ⟨2, + \infty)$ oraz otrzymanego zbioru rozwiązań: $x \leq \frac{5}{2} = 2 \frac{1}{2}$ i otrzymujemy, że w tym przypadku rozwiązaniami nierówności są $x \in ⟨2, 2 \frac{1}{2}⟩$ .
$|x + 1| - |x - 5| \geq x - 3$ .
Korzystając z definicji wartości bezwzględnejwartości bezwzględnej, otrzymujemy:
$|x + 1| = \{\begin{cases} x + 1, dla x \geq - 1 \\ - x - 1, dla x < - 1 \end{cases}$
oraz
$|x - 5| = \{\begin{cases} x - 5, dla x \geq 5 \\ - x + 5, dla x < 5 \end{cases}$ .
Wobec tego rozpatrujemy na osi liczbowejoś liczbowaosi liczbowej trzy przedziały:
$(- \infty, - 1)$ , $⟨- 1, 5)$ oraz $⟨5, + \infty)$ .
Otrzymujemy trzy następujące przypadki:
1. $x \in (- \infty, - 1)$ ; wtedy $|x + 1| = - x - 1$ oraz $|x - 5| = - x + 5$ ,
2. $x \in ⟨- 1, 5)$ ; wtedy $|x + 1| = x + 1$ oraz $|x - 5| = - x + 5$ ,
3. $x \in ⟨5, + \infty)$ ; wtedy $|x + 1| = x + 1$ oraz $|x - 5| = x - 5$ .
Wynika stąd, że:
- w przypadku pierwszym otrzymujemy nierówność $- x - 1 - (- x + 5) \geq x - 3$ ,
  skąd $- x - 1 + x - 5 \geq x - 3$ ,
  $- 1 - 5 + 3 \geq x$ ,
  czyli $x \leq - 3$ .
  Bierzemy część wspólną założonego przedziału: $x \in (- \infty, - 1)$ oraz otrzymanego zbioru rozwiązań: $x \in (- \infty, - 3)$ i otrzymujemy, że w tym przypadku rozwiązaniami nierówności są $x \in (- \infty, - 3)$ .
- w przypadku drugim otrzymujemy nierówność
  $x + 1 - (- x + 5) \geq x - 3$ ,
  $x + 1 + x - 5 \geq x - 3$ ,
  skąd $x \geq - 3 - 1 + 5$ ,
  czyli $x \geq 1$ .
  Bierzemy część wspólną założonego przedziału: $x \in ⟨- 1, 5)$ oraz otrzymanego zbioru rozwiązań: $x \in ⟨1, + \infty)$ i otrzymujemy, że w tym przypadku rozwiązaniami nierówności są $x \in ⟨1, 5)$ .
- w przypadku trzecim otrzymujemy nierówność
  $x + 1 - (x - 5) \geq x - 3$ ,
  skąd $x + 1 - x + 5 \geq x - 3$ ,
  $1 + 5 + 3 \geq x$ ,
  czyli $x \leq 9$ .
  Bierzemy część wspólną założonego przedziału: $x \in ⟨5, + \infty)$ oraz otrzymanego zbioru rozwiązań: $x \in (- \infty, 9⟩$ i otrzymujemy, że w tym przypadku rozwiązaniami nierówności są $x \in ⟨5, 9⟩$ .
Sumując przedziały otrzymane w każdym z rozpatrywanych przypadków, dostajemy, że rozwiązania danego równania to $x \in (- \infty, - 3) \cup ⟨1, 5) \cup ⟨5, 9⟩$ , czyli $x \in (- \infty, - 3) \cup ⟨1, 9⟩$ .

Słownik

oś liczbowa

prosta, na której wyróżniono zwrot i punkt $O$ zwany zerowym oraz ustalono odcinek jednostkowy

wartość bezwzględna liczby rzeczywistej

wartością bezwzględną liczby rzeczywistej $x$ nazywamy jej odległość na osi liczbowej od zera; wartość bezwzględną liczby $x$ oznaczamy symbolem $|x|$

nierówność trójkąta

dla dowolnych liczb rzeczywistych $a$ i $b$ prawdziwa jest nierówność
$|a + b| \leq |a| + |b|$ ,
przy czym równość zachodzi w niej wtedy i tylko wtedy, gdy $a b \geq 0$

Wprowadzenie

Test samosprawdzający

Słownik