Zastanówmy się, jak wysoko znajduje się skoczek narciarski, siedząc na najniższej możliwej belce startowej.

Oczywiście, możemy poradzić sobie z problemem, korzystając z twierdzenia Pitagorasa oraz podobieństwa trójkątówpodobieństwo trójkątówpodobieństwa trójkątów. Jest to jednak okrężna droga. Wykorzystamy zatem trygonometrię, aby uprościć problem.

Możemy łatwo policzyć cosinus kąta $\alpha$ – kąta nachylenia skoczni:

$\cos \alpha =\frac{80,85}{98,7}\approx 0,82$.

R17Mu67IVUzpU

Ilustracja przedstawia trójkąt prostokątny leżący na dłuższej przyprostokątnej. W trójkącie poprowadzono odcinek o długości x który jest równoległy do krótszej przyprostokątnej i łączy dłuższą przyprostokątną z przeciwprostokątną. Kąt alfa znajduje się pomiędzy przeciwprostokątną, a podstawą trójkąta. Nad przeciwprostokątną znajduje się równanie $98,7-22=76,7$.n>7.

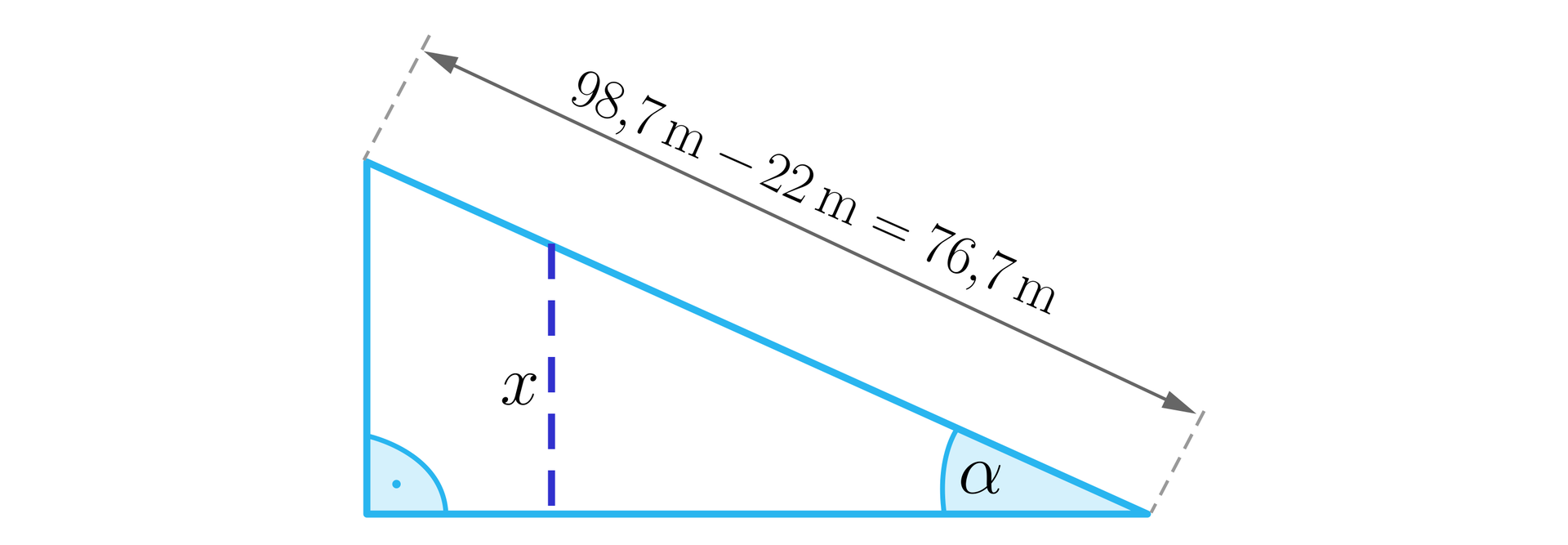
Rozważmy teraz trójkąt prostokątny, którego przyprostokątną jest szukana wysokość. Znamy przeciwprostokątną tego trójkąta oraz $\cos \alpha$. Pamiętajmy, że $x$ jest przyprostokątną leżącą na przeciw kąta $\alpha$, więc powinniśmy korzystać z wartości $\sin \alpha$.

Jak ją znaleźć?

Przypomnijmy sobie tożsamości trygonometrycznetożsamości trygonometrycznetożsamości trygonometryczne, a konkretnie jedynkę trygonometrycznąjedynka trygonometrycznajedynkę trygonometryczną:

${\sin }^2\alpha +{\cos }^2\alpha =1$.

Stąd ${\sin }^2\alpha =1-{\cos }^2\alpha \approx 1-{\left(0,82\right)}^2=0,3276$,
więc $\sin \alpha \approx 0,57$ lub $\sin \alpha \approx -0,57$.

Wiemy jednak, że kąt $\alpha$ jest ostry, więc wybieramy dodatnią wartość funkcji sinus.

Zatem $\frac{x}{76,5}\approx 0,57$, stąd $x\approx 43,61 \mathrm{m}$.

Na jakiej wysokości znajduje się skoczek siedząc na najniższej belce? To

$43,61$ $\mathrm{m}$ $+$ $89,11$ $\mathrm{m}$ $=$$132,72$ $\mathrm{m}$.

Znając $\sin \alpha$, możemy łatwo policzyć na jakiej wysokości znajduje się skoczek siedząc na każdej z $35$ belek startowych.

Korzystając z poniższego rysunku, obliczymy $\sin \beta$ i $\cos \beta$.

RUbz5UhwCETA6

Ilustracja przedstawia dwa kąty przyległe alfa oraz beta. Kąt alfa posiada dwa ramiona, pierwsze zawarte w prostej poziomej na której leżą oba kąty oraz drugie wspólne z kątem beta. Kąt alfa jest kątem trójkąta prostokątnego o przyprostokątnych pierwszej pionowej o długości równej trzy i drugiej poziomej o długości równej cztery.

Rozwiązanie: Zacznijmy od policzenia wartości $\sin \alpha$. Widzimy, że kąt $\alpha$ jest kątem trójkąta prostokątnego o przyprostokątnych $3$ i $4$.

R1PHFKPhJNgqM

Ilustracja przedstawia dwa kąty przyległe alfa oraz beta. Kąt alfa posiada dwa ramiona, pierwsze zawarte w prostej poziomej na której leżą oba kąty oraz drugie wspólne z kątem beta. Kąt alfa jest kątem trójkąta prostokątnego o przyprostokątnych, pierwszej pionowej o długości równej trzy i poziomej o długości równej cztery.

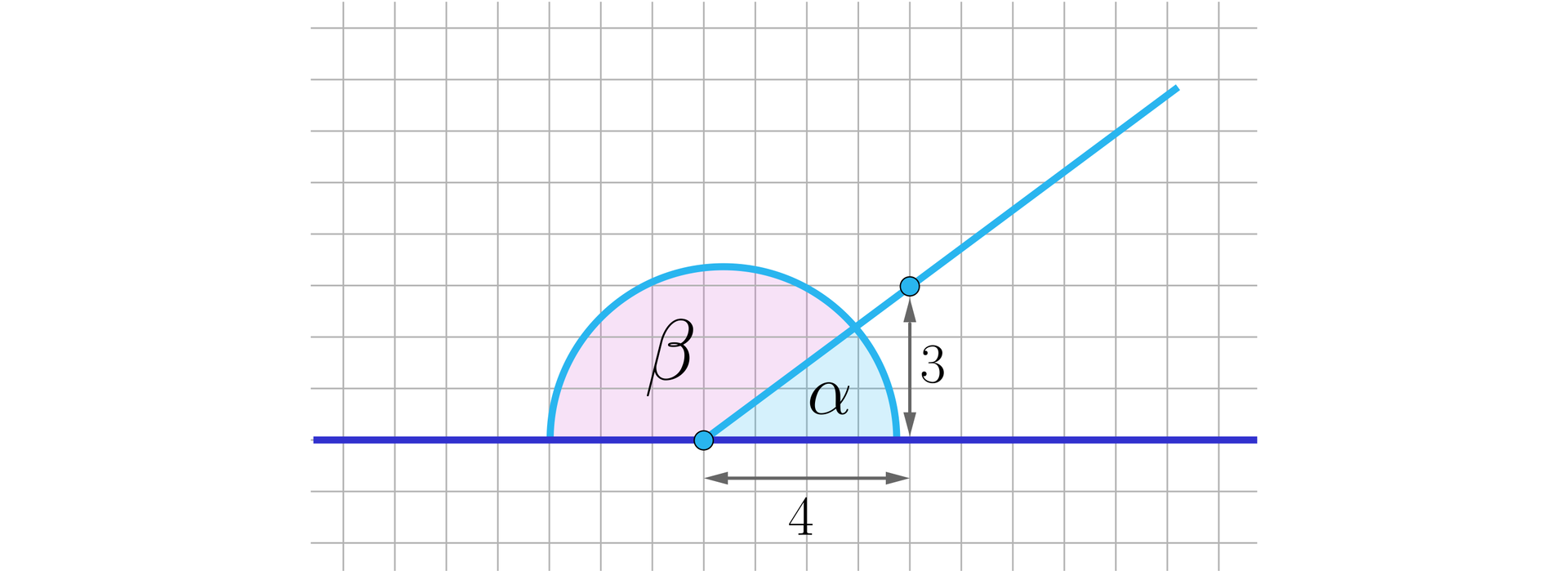
Z twierdzenia Pitagorasa długość przeciwprostokątnej to $5$. Zatem $\sin \alpha =\frac{3}{5}$.

Kąty $\alpha$ i $\beta$ to kąty przyległe, więc $\alpha +\beta =180°$, zatem $\sin \alpha =\sin \beta$.

Znamy już $\sin \beta =\frac{3}{5}$. Pozostaje wyliczyć $\cos \beta$. Znów skorzystamy z jedynki trygonometrycznej:

${\cos }^2\beta =1-{\sin }^2\beta =1-\frac{9}{25}=\frac{16}{25}$.

Zatem $\cos \beta =\frac{4}{5}$ lub $\cos \beta =-\frac{4}{5}$. Widzimy jednak, że $\beta$ jest kątem rozwartym, więc $\cos \beta <0$.

Otrzymujemy więc odpowiedzi: $\sin \beta =\frac{3}{5}$ i $\cos \beta =-\frac{4}{5}$.

Wiedząc, że $\cos \alpha =-\frac{3}{7}$ oraz $\alpha \in \left(\frac{3}{2}\pi ,2\pi \right)$ obliczymy $\sin \alpha$.

Rozwiązanie: Na mocy jedynki trygonometrycznej otrzymujemy, że ${\sin }^2\alpha =1-{\left(\frac{3}{7}\right)}^2=\frac{40}{49}$. Zatem $\sin \alpha =\frac{2\sqrt{10}}{7}$ lub $\sin \alpha =-\frac{2\sqrt{10}}{7}$. Korzystając z powyższej tabeli możemy ustalić, że $\sin \alpha =-\frac{2\sqrt{10}}{7}$.

Wiedząc, że ${\cos }^2\alpha =\frac{1}{2}$ oraz $\alpha \in \left(\pi ,\frac{3}{2}\pi \right)$ obliczymy $\sin \alpha$.

Rozwiązanie: Rozwiążemy powyższe zadanie na dwa sposoby.

Sposób $\text{I}$

Zaczniemy od wyznaczenia wartości funkcji $\cos \alpha$. Korzystając ze wzoru skróconego mnożenia otrzymujemy równanie $\left(\cos \alpha -\frac{\sqrt{2}}{2}\right)\left(\cos \alpha +\frac{\sqrt{2}}{2}\right)=0$. Stąd $\cos \alpha =\frac{\sqrt{2}}{2}$ lub $\cos \alpha =-\frac{\sqrt{2}}{2}$. Ponieważ $\alpha \in \left(\pi ,\frac{3}{2}\pi \right)$, więc $\cos \alpha =-\frac{\sqrt{2}}{2}$. Postępując analogicznie jak w Przykładzie 3 otrzymujemy, że ${\sin }^2\alpha =\frac{1}{2}$. Dla rozważanego kąta $\alpha$ zachodzi nierówność $\sin \alpha <0$, więc $\sin \alpha =-\frac{\sqrt{2}}{2}$.

Sposób $\text{II}$

W omawianym przykładzie znalezienie dokładnej wartości funkcji $\cos \alpha$ nie jest konieczne. Wystarczy rozważyć układ równań $\left\{\begin{array}{l}{\cos }^2\alpha =\frac{1}{2}\\ {\sin }^2\alpha +{\cos }^2\alpha =1\end{array}\right.$ aby otrzymać, że ${\sin }^2\alpha +\frac{1}{2}=1$ i tym samym, skoro $\sin \alpha <0$, to $\sin \alpha =-\frac{\sqrt{2}}{2}$.

Wiedząc, że $\cos \alpha =2-\sqrt{2}$ oraz że kąt $\alpha$ jest kątem ostrym obliczymy wartość wyrażenie $\frac{\cos \alpha }{\sin \alpha }$.

Rozwiązanie: Korzystając z jedynki trygonometrycznej, mamy, że ${\sin }^2\alpha =1-{\left(2-\sqrt{2}\right)}^2=1-\left(4-4\sqrt{2}+2\right)=1-\left(6-4\sqrt{2}\right)=4\sqrt{2}-5$. Stąd $\sin \alpha =\sqrt{4\sqrt{2}-5}$ lub $\sin \alpha =-\sqrt{4\sqrt{2}-5}$. Wszystkie wartości funkcji trygonometrycznych kąta ostrego są dodatnie, więc $\sin \alpha =\sqrt{4\sqrt{2}-5}$.

Zatem $\frac{\cos \alpha }{\sin \alpha }=\frac{2-\sqrt{2}}{\sqrt{4\sqrt{2}-5}}=\frac{\left(2-\sqrt{2}\right)\sqrt{4\sqrt{2}-5}}{4\sqrt{2}-5}=\frac{\left(2-\sqrt{2}\right)\sqrt{4\sqrt{2}-5}}{4\sqrt{2}-5}·\frac{4\sqrt{2}+5}{4\sqrt{2}+5}=\frac{\left(3\sqrt{2}+2\right)\sqrt{4\sqrt{2}-5}}{7}$

zależności między funkcjami trygonometrycznymi, będące prawdziwe, bez względu na wartość kąta

jedna z tożsamości trygonometrycznych: dla dowolnego kąta $\alpha$ spełniona jest równość ${\sin }^2\alpha +{\cos }^2\alpha =1$

trójkąty podobne to trójkąty, które mają pary kątów tej samej miary